基于卷积神经网络的OFDM-UWB信道环境识别
2021-07-26职如昕陈晋辉
王 斐,徐 湛,2,职如昕,2,陈晋辉,2
(1.北京信息科技大学信息与通信工程学院,北京100101;2.北京信息科技大学现代测控技术教育部重点实验室,北京100101)
0 概述
超宽带(Ultra-WideBand,UWB)无线通信是一种基于低能量短时脉冲的无线通信技术,近年来在无线通信和测距领域被广泛应用。得益于自身巨大带宽的优势,超宽带无线通信技术具有良好的材料穿透能力,同时良好的时间分辨率也使其适用于精确测距[1]。基于以上优势,目前超宽带已成为室内定位的主流技术。非视距(Non-Line of Sight,NLOS)传播是超宽带技术误差的主要来源之一,在进行室内定位时,信道中的遮挡会使信号在传输过程中产生大量的损耗,从而严重影响定位精度[2]。因此,识别出信道是否属于非视距传输对于提升定位精确度具有重要意义。
目前,研究者提出了许多非视距信道的识别方法。文献[3]基于定位时间(Time-of-Arrival,TOA),利用CayleyMenger行列式(CayleyMenger Determinant,CMD)构建的假设检验模型进行NLOS 信道识别。文献[4]基于距离测量的贝叶斯先验概率,利用贝叶斯顺序检验的方法进行LOS/NLOS 识别。文献[5]根据物理层的相位特征和OFDM 的子载波频率分集提出一种LOS 识别方案。文献[6-8]通过假设检验法来进行NLOS 信道环境的识别。信道识别的关键在于信道识别参数,例如利用支持向量机算法对信道特征参数[9-10]、移动台与基站的特征参数[11]、峭度[12-14]以及信号能量[15-16]进行训练和识别。
传统的LOS/NLOS 识别方法较少利用信道统计模型,并且都需要事先进行大量的数据采集,在不同场景下,不同的信号特征使得识别的工作量很大。此外,多数方法需要预设门限值,而阈值的可靠性和鲁棒性也存在争议。为突破传统识别方法的局限性,本文提出一种新的分类方法。利用信道估计的冲激响应构建数据集,将通信信道识别问题转化为图像识别问题,对其经短时傅里叶变换(Short-Time Fourier Transform,STFT)处理后通过卷积神经网络来进行正确识别分类。在此基础上,基于OFDM 方案的UWB 系统进行仿真,通过加入高斯白噪声验证所提方法的实用性。
1 IEEE 802.15.3a UWB 信道统计模型
“分簇”是描述室内超宽带传输特性的最优方式之一,受到了研究人员的广泛认同,即构建S-V 模型。在S-V 模型的定义中,脉冲信号各径上的分量以一簇一簇传输的方式到达接收机。簇和簇内射线的到达时间服从泊松随机过程分布。先后到达的多径信号增益统计独立,多径信号的平均功率(幅度的均方值)随簇和簇内射线双指数衰减,其幅度呈瑞利分布,相位在[0,2π)内均匀分布。S-V 模型的信道冲激响应可以表示为:

在式(1)中:Tl(l=0,1,…)为第(l+1)个到达簇的到达时间,T0=0 表示第1 个到达簇的到达时间;τk,l(k=0,1,…)为第(l+1)个簇中第(k+1)个到达射线的到达时间,τ0,l表示第l个簇中第1 条射线的到达时间;βk,l为第(l+1)个簇中第(k+1)个到达射线的多径增益,其相位为θk,l。S-V 模型中其他主要参数还包括多径到达时间分布、多径增益分布、多径相位分布等。
表1 列出了IEEE 802.15.3a 室内信道模型的典型参数,其中数据由大量实测数据推导得出,CM1表示视距传播模型(0 m~4 m),CM2 表示非视距传播模型(0 m~4 m),CM3 表示非视距传播模型(4 m~10 m),CM4 表示一个极端非视距传播模型多径信道,Λ表示簇平均到达速率,λ表示脉冲平均到达速率,Γ表示簇的功率衰减因子,γ表示簇内脉冲的功率衰减因子,δξ表示簇的信道系数标准偏差,δζ表示簇内脉冲的信道系数标准偏差,δg表示信道幅度增益的标准偏差。

表1 IEEE 802.15.3a UWB 信道参数Table 1 IEEE 802.15.3a UWB channel parameters
2 基于卷积神经网络的信道环境识别
卷积神经网络在近年来被广泛应用于多分类任务[17-19],特别是图像分类[20]。使用CNN 进行LOS/NLOS信道环境识别的优点是避免了对特征参数的大量计算。同时,在训练过程中,卷积神经网络可以自行选择合适的权值。CNN 提取的特征比人工提取的特征更有效。在前期研究[21]中,为增强图像特征,得到更有效的数据集,研究者对信道冲激响应进行STFT处理得到脉冲响应谱。以不同的颜色表示不同的能量强度,将信道识别问题转化为图像识别问题。利用MATLAB 对IEEE 802.15.3a UWB 信道统计模型进行仿真,得到CM1~CM4 这4 种信道环境下的冲激响应,如图1所示,其经STFT 处理后如图2所示。分析结果表明,CM1~CM4 这4 种情况下的脉冲响应具有不同的特征。

图1 CM1~CM4 信道环境下的冲激响应Fig.1 Impulse responses under CM1~CM4 channel environments

图2 STFT 处理后的冲激响应Fig.2 Impulse responses after STFT processing
将短时傅里叶变换后的图像作为数据集进行训练识别。CM1~CM4 信道环境的数据集规模均为48 000 个数据,其中38 400 个数据作为训练集,剩余数据作为测试集。
图3 为卷积神经网络对信道冲激响应的识别率曲线,其中:2conv_1fc 表示两卷积层一全连接层;2conv_2fc 表示两卷积层两全连接层;3conv_1fc 表示三卷积层一全连接层;3conv_2fc 表示三卷积层两全连接层。可以看出,该方法对于理想情况下视距和非视距信道的识别率最高可达98.24%。

图3 卷积神经网络对信道冲激响应的识别率Fig.3 Recognition rate of CNN for channel impulse response
3 OFDM-UWB信道环境识别
本文OFDM 方案的UWB 通信系统通过QPSK星座调制的128 个载波来符合“500 MHz 带宽”的要求,合成信号占用一个528 MHz 的信道。仿真中利用IEEE 802.15.3a UWB 模型所生成的冲激响应构建信道环境。
OFDM 系统一个重要的优势在于可以利用快速傅里叶变换(Fast Fourier Transform,FFT)生成,极大地降低了系统的复杂度。数据比特被调制为QPSK 符号,随后通过逆FFT(IFFT)被转化为时域数据发送到无线信道中。由于无线信道的影响,接收信号通常会发生失真,多径传播的频域模型由式(2)表示:

其中:Y表示接收端的信号向量;X表示发射端的信号向量;H表示信道频率响应;Z表示高斯白噪声。为消除无线信道对信号传输的影响,必须在接收端对信道频率响应H进行估计从而对接收信号进行补偿。根据式(2),使用LS(最小二乘)信道估计得出信道频率响应:

其中,X[k]表示第k个子载波上的导频信号,Y[k]表示接收到的导频信号,HLS[k]表示估计出的频率响应。
对频率响应的估计结果做IFFT 变换后得到4 种信道环境下的冲激响应,分别如图4所示。

图4 信道估计冲激响应Fig.4 Impulse responses estimated by the channel
STFT 将一维的hLS转换为二维时频图,这有利于信道环境的识别。离散的STFT 表达式为:

其中,w(m-n)表示窗函数,n表示窗长。在时域用窗函数将hLS截取为多段,对每一段做傅里叶变换,求出各段的频域特性,从而求出hLS的时频特性。为克服窗与窗内数据的关联性,相邻两窗部分重叠,仿真中重叠大小参数为Noverlap。
Hamming 窗能够有效减小频谱泄露问题,本文选取Hamming 窗函数,如式(5)所示:

其中,0≤k≤n-1。经STFT 处理所得不同信道下hLS时频图如图5所示。

图5 STFT 处理后的信道估计冲激响应Fig.5 Impulse responses estimated by the channel after STFT processing
在STFT 处理过程中,不同的窗长n以及参数Noverlap 会使图像的分辨率发生改变,导致图像特征有所差异。本文在多次仿真测试基础上,选择长度n为8 的Hamming 窗,将参数Noverlap 设置为7。
在OFDM 方案的UWB 系统中,不同的比特信噪比(EbN0)下信道估计的准确性也会随之浮动。仿真在最高效的STFT 参数下基于不同的EbN0 值进行。
4 仿真与结果分析
在不同的STFT 参数下,使用不同结构卷积神经网络的识别率如表2所示。该部分测试中EbN0为30 dB。数据显示,基于线性变换的参数n和Noverlap,相同结构神经网络下的信道识别率呈非线性变化。使用不同的窗长n和Noverlap 会使STFT 的结果具有不同的时域解析度及频域解析度,两者相互冲突,无法同时获得高解析度。使用短窗STFT 则时间分辨率高,使用长窗则频率分辨率高。原始数据被窗函数分割后,窗口两端位置的信息就会减少,Noverlap 的存在改善了这种边缘效应。在相同的窗长n下,重叠度越高,则STFT 的时频分析图像越平滑,结果越准确。

表2 各STFT 参数下卷积神经网络的识别率Table 2 Recognition rate of CNN under different STFT parameters
根据表2所示数据,选取结果最优值为:n=8,Noverlap=7,使用两个卷积层两个全连接层的神经网络进行仿真。在不同EbN0 下的识别率如图6所示。从中可以看出,随着EbN0 值的增大,本文方法对信道环境的识别率稳定上升,在EbN0 值为20 dB左右趋于稳定,此时识别率为90.572 9%。

图6 不同EbN0 下4 种信道环境的识别率Fig.6 Recognition rate of four channel environments under different EbN0
根据参考文献[21]提取以下信道特征参数:
1)平均附加时延。此项参数即信道冲激响应功率延迟分布的一阶矩,表达式如下:

其中:G表示信道总能量;αn表示幅度增益;τn表示附加时延。
2)均方根时延扩展。此项参数与平均附加时延的本质相似,其由平均附加时延的标准差所计算得出,表达式如下:
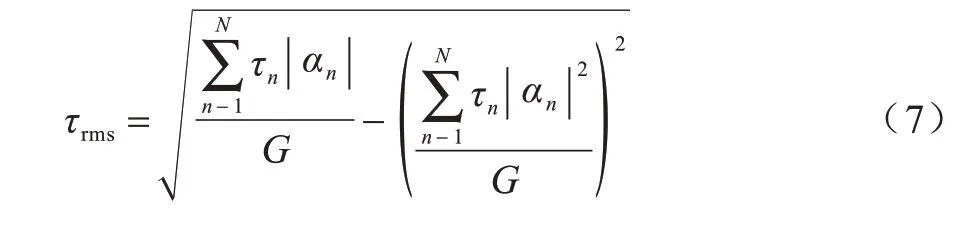
3)幅度高于峰值50%的径的数量。此项参数反映了信道多径的分布情况,表达式如下:

其中,hmax表示冲激响应最大幅度。
4)占据信道85%能量的径的数量表达式如下,该参数同样表征了信道中多径的分布情况。

其中,Ece(n)表示累积能量分布。
使用较为传统的信道识别方式,基于信道特征参数,利用支持向量机对信道环境进行识别,识别结果与本文方法识别结果的对比如图7所示。可以看出,在加入噪声的多带OFDM 超宽带信道识别问题中,CNN 的识别能力同样优于SVM 的识别能力,通过横向对比,进一步验证了本文方法的有效性。

图7 不同EbN0 下2 种方法的识别率对比Fig.7 Comparison of recognition rates between two methods under different EbN0
5 结束语
本文提出一种基于CNN 的LOS/NLOS 信道环境识别方法。对信道脉冲响应图像做短时傅里叶变换处理后,作为CNN 的输入进行模型训练,把信道识别问题转化为图像识别问题。针对4 种室内UWB信道环境,在OFDM 方案的UWB 系统下进行仿真,结果表明,随着EbN0 的增加,该方法的识别率逐渐提高,在EbN0 为20 dB 左右趋于稳定,识别率达到90.572 9%。与传统识别方法的比较结果也验证了该方法的有效性和优越性。后续将进一步验证本文方法对于其他类型无线通信链路的实用性,同时不仅局限于加入高斯白噪声,而将考虑加入干扰等非理想因素,设计用于OFDM 超宽带信道识别的神经网络。
