压缩感知改进探地雷达回波信号时延估计

杜改丽，刘师良，程德红

（1.河南医学高等专科学校，河南 郑州 450091；2.辽宁对外经贸学院，辽宁 大连 116052）

1 引言

探地雷达以电磁波作为介质，通过地下介质的电磁特性差异和回波特性实现对地下浅层目标的特征信息提取和地质探测，且具有较高的探测分辨率，具有便携无损、过程连续、精准高效等优势，近年来被广泛应用于道路质量检测、安防、军事、考古等领域[1]。不同地质目标的特性主要体现在雷达回波信号的幅值和时延参数中，而由于介质大尺寸颗粒反射、电导率不一致及天线耦合等因素，回波信号中含有大量杂波分量，且衰减少、时间上相互重叠增强，导致真实目标信号被淹没，为此，提高探地雷达回波信号的时延和幅值提取精度，是提高目标检测准确性的，已成为当前该领域研究的热点[2]。

目前，对回波信号的时延处理主要包括时域信号时延估计和频域信号时延估计两个方向[3]，时域处理方法由回波信号通过滤波器等方法直接分离出目标特性相关信息，而频域处理则通过小波变换、FFT等提取回波信号的频域信息，进而计算目标相关特性[4]。匹配滤波[5]方法难以处理时域交叠，环境杂波较强时会对幅值较小的回波产生覆盖，严重降低探测性能；FFT方法[6]的时延估计依赖系统带宽，但系统又受到环境、功耗及尺寸的各种限制，难以有效平衡；小波变换方法[7]对特定频率范围的噪声或信号与噪声频率不相关情况下，具有较好的时延估计，但对白噪声处理效果不佳。为了解决上述问题，多重分类和旋转不变等基于多分辨谱估计的回波时延估计算法被提出，以提高抗噪性能，但其要求信号具有较高的相关性[8]。主成分分析、经验模态分解、以及奇异值分解等基于统计特性的滤波技术也逐渐应用于探地雷达回波信号提取及杂波抑制，这些方法主要基于杂波和目标之间的幅值差异来检测回波有用成分，但特性差异的边界往往不明显，而边界选取又是至关重要的，甚至影响最终检测质量[9]，造成虚假目标干扰。

压缩感知（Compressive Sensing，CS）表明，通过非线性的优化算法，可以由少量观测数据实现可压缩信号的精确重构，从而避免大规模数据测量的需要，并降低数据采样速率的要求，文献[10]提出一种离散差分进化压缩感知算法，以缓解传统方法对稀疏度的依赖，了采用粒子编码替代稀疏度未知的信号，并通过迭代优化实现信号的精确重构，并应用于雷达回波信号重构；文献[11]以压缩感知构建雷达中频信号处理的欠定方程，从而通过少量内积运行实现谱峰的高效捕获，缓解已有算法计算量较大、精度不高问题。

根据已有压缩感知算法研究，为提高探地雷达回波信号的时延估计精度，文中提出压缩感知回波重构优化的探地雷达时延估计算法，算法首先基于探地雷达回波特性分析压缩感知应用于回波延时估计的可行性，然后，构建了压缩感知回波时延估计模型，并采用QR分解优化的快速正交匹配追踪对时延估计模型进行求解，降低基函数错选概率，提高模型收敛速度。仿真实验验证算法的有效性。

2 回波信号模型

式中：s(t)—发射信号；τk—回波时延。回波时延估计即为在接收机回波r(t)中准确估计出τk。设地面目标距离接收机天线距离为R，则其回波信号可表示为：

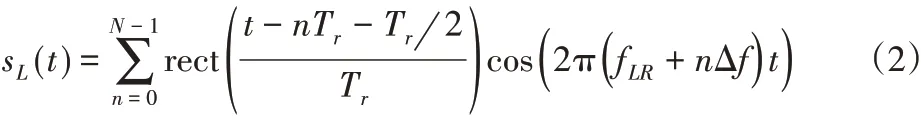
式中：Tr—脉冲周期；fLT、Δf—起始载频频率及其步进；N—步进数；fLR—接收机加波起始频率。将探地雷达的本振信号与回波信号进行混频后，得到：

探地雷达的探测目标通常为固定目标，因而式（4）的第一项通常为常数项，而第二项为离散信号，其时间点为2R/C，频率呈线性变化，这样，对采样后信号进行FFT逆变换后，可以得到精确2R/C，进而计算目标距离R。

将实际环境干扰噪声n(t)加入到雷达接收机回波信号模型，则实际回波模型为：

3 压缩感知优化回波时延估计

设基向量B={bk|k=1，2，k} 为空间Rk的原子集，则对于任意信号x∈Rk，可以由基向量B线性表示为：

式中：θ—线性投影系数矢量，当‖θ‖0=S(S≤K)时，称信号x为稀疏的。当信号为稀疏时，可以通过矩阵H∈Rk（H与B不相关）对其进行线性观测，从而可以得到未知参数的观测向量y∈Rk为：

与标准的农民专业合作社相比较，农机合作社更强调入社的股份(包括农机折价形成的股份)，这是由于农机的价值较大，同时合作社股份构成较为复杂(农机、土地、资金等)，但在管理方式上依然强调民主，强调民办、民管、民受益。农机合作社是中国农民对于世界合作社运动的重要贡献。

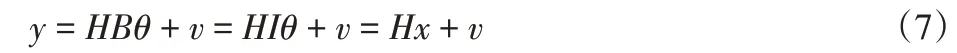
式中：v—噪声矩阵。根据压缩感知理论，如果H满足RIP[9]条件，

即存在参数δ∈()

0，1 使信号x满足不等式：

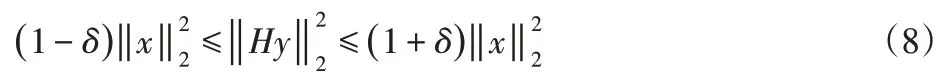
式中：‖x‖2—信号x的欧几里德范数，则信号x可以通过观测向量进行重构。重构信号x可以通过求解l0范数最小化问题实现，但l0范数最小化问题求解较为困难，通常选择将其转化为凸的l1范数优化问题，即目标函数为：

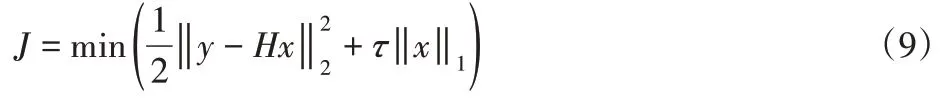
式中：τ—稀疏度控制正则化参数。

由于探地雷达发射的电磁波信号是已知的，而其回波信号通常为稀疏的，因此，以发射信号作为基带原子集对回信号波进行稀疏分解，基函数字典可表示为：

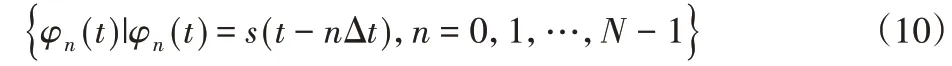
式中：N—字典集规模；Δt=1/B—回波信号时延；B—雷达带宽，则基于基函数的压缩感知数据采样过程为：

目前，基于解压缩感知的雷达回波信号重构通常采用贪婪类算法或凸优化类算法，其中正交匹配追踪（Orthogonal Matching Tracking，OMP）算法应用较为广泛，但传统匹配追踪算法迭代过程复杂，不适宜雷达回波信号的实时提取要求，为引，提出一种改进的快速OMP优化重构算法。

传统OMP算法需要在每次迭代中处理最小二乘求解，即：

基于上述快速算法，在进行探地雷达回波信号重构过程中，首先，为避免快速重构基函数的匹配度不足导致函数无法收敛，选取匹配度最优的2K个基函数作为子字典集，以保证子字典集中包含有稀疏分解所需的最优匹配基函数；然后，利用上述快速稀疏分解和重构算法代替传统的最小二乘算法对基函数进行迭代求解；最后以迭代求解后的匹配度最优的K个基函数作为稀疏分解的最优匹配基函数。

改进后的正交匹配追踪算法步骤为：

（1）初始化。输入回波信号矢量z，初始化迭代初始值r0=z，k=0，Ψ0=[]，R=[]，最大迭代数K，原子集s=∅以及p0=

（2）计算s=∅中各基函数与z的匹配度值，排序后选出前2K个基函数组成子集；

（3）利用快速OMP算法进行信号逼近

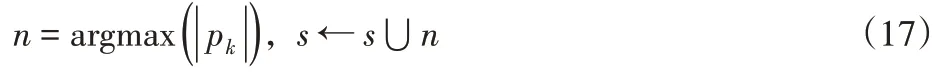
并根据排序选取K个基函数组成新子集；

（4）根据QR分解，计算相关变量

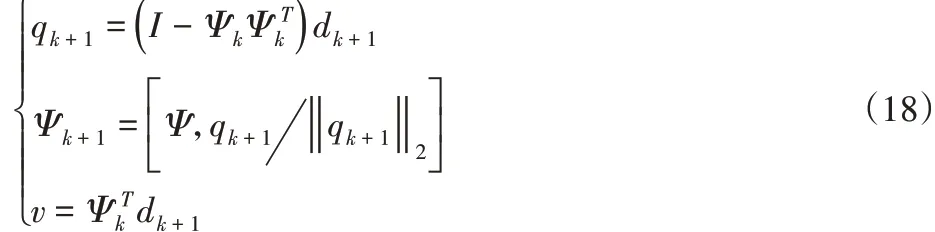
（5）根据式（16）计算并更新R-1

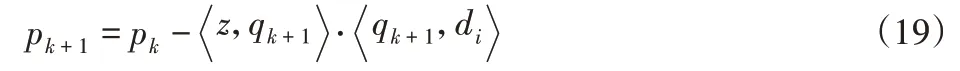
（6）判断是否满足终止条件，如满足输出重构基函数ck=如不满足，返回（2）。

4 仿真试验分析

为验证文中提出的改进OMP 回波时延估计算法的估计性能，以线性调频脉冲信号作为实验雷达发射信号的调制波形，接收机输出的信号频率f0=25MHz，脉宽Tb=0.2us，带宽B=25MHz。假回波三分量的延分别为0.459us，0.821us和0.842us，信噪比20dB。

4.1 算法时延估计有效性验证

以文中方法对实验回波进行时延估计，实验结果，如图1所示。原始信号的波形，如图1（a）所示。这里算法估计的回波时延，如图1（b）所示。从实验结果可以看出，回波二分量强度达到三分量强度的2倍，且两个回波时延较近，但这里算法仍能较清晰的分辨现两个回波时延，且对分量强度不第三，且具有较高的估计分辨率，从而验证算法的时延估计有效性。

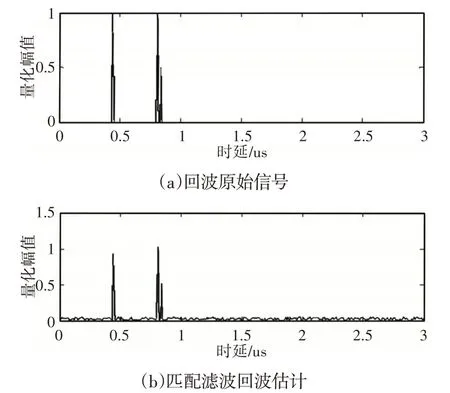
图1 不同算法对回波估计结果的比较Fig.1 Comparison of Estimated Results of Different Algorithms

4.2 估计性能比较实验

为进一步分析算法性能，将其与子空间追踪（SPP）算法、传统OMP算法、前后向分段OMP（FBStOMP）算法及匹配波滤（Mat-Fil）算法进行实验比较，稀疏度以5为步长由0至50，以重构成功率和相对误差作为评价指标，每种算法重复100次，取实验结果的平均值，实验结果，如图2、图3所示。实验结果表明，匹配滤波方法不能有效应对强回波遮盖其重构成功率不高，重构误差较大，OMP、FBstOMP 及算法都是基于压缩感知，对强回波覆盖具有较好的适应性，因而取得较好的实验结果，而算法的重构成功率最高，相对误差最小，这是因为算法有效提高了基函数与回波信号的匹配程序，避免基函数错选，从而提高了重构回波的信噪比，时延估计性能。

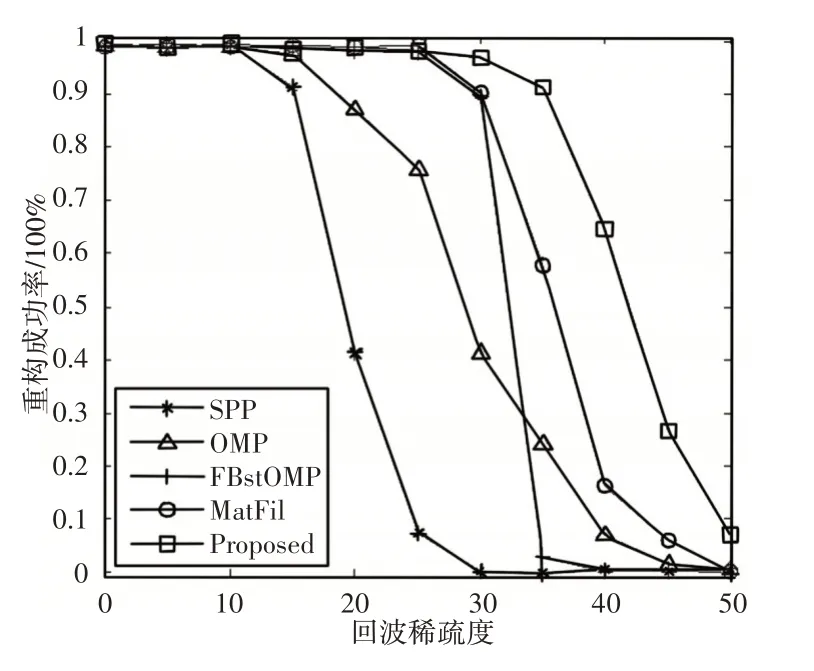
图2 不同算法的回波重构成功率比较Fig.2 Comparison of Echo Reconstruction Rates of Different Algorithms

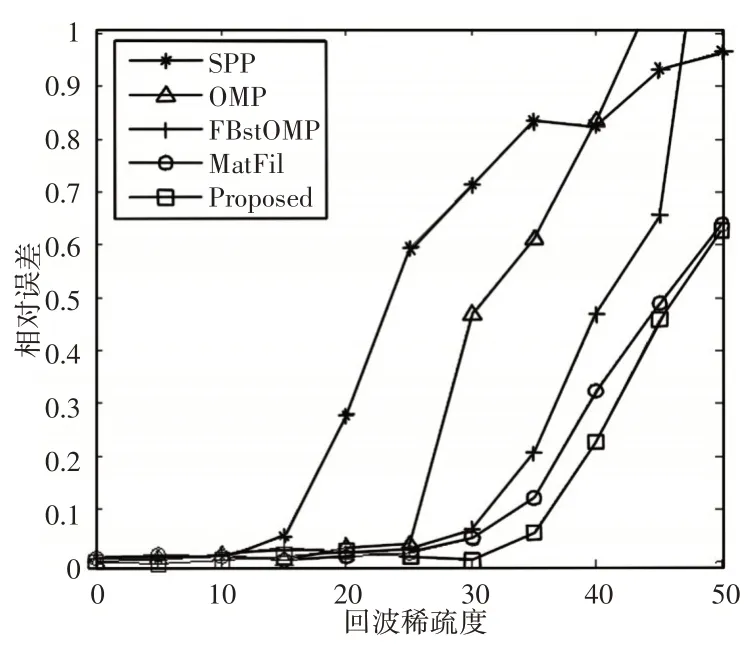
图3 不同算法的回波重构误差比较Fig.3 Comparison of Echo Reconstruction Errors of Different Algorithms

5 结束语

针对探地雷达回波强干扰信号覆盖导致时延估计精度不高问题，提出了一种压缩感知回波重构优化的探地雷达时延估计算法，算法首先基于探地雷达回波特性分析压缩感知应用于回波延时估计的可行性，然后，构建了压缩感知回波时延估计模型，并采用QR 分解优化的快速正交匹配追踪对时延估计模型进行求解，降低基函数错选概率，提高模型收敛速度。仿真实验结果验证了该方法的有效性。