质点的运动轨迹是圆的渐开线吗*

姜付锦 李 弼

(武汉市黄陂一中 湖北 武汉 430300)

张 静

(江苏省淮阴中学 江苏 淮安 223002)

《物理教学》在2017年第6期发表了一篇关于一道浙江大学自主招生题的分析[1]，原文中虽然给出了质点的最终速度大小和方向，但没有给出推导过程，原文还认为质点运动轨迹是圆的渐开线，但是笔者以为这个分析有待商榷.本文尝试从动力学角度出发，得到质点动力学微分方程组，并给出质点运动规律的数值模拟解.

1 题目

【题目】如图1所示，在倾角为θ的粗糙斜面上存在垂直斜面向上的匀强磁场B，在斜面上由静止释放一个带正电质点.设质点的质量为m，带电荷量为+q，斜面的动摩擦因数为μ，重力加速度为g，若斜面足够大，试分析质点最终的运动状态和运动轨迹是怎样的？

图1 质点初始位置图

2 最大速度的分析

如图2所示，以质点释放位置为坐标原点，水平向右为x轴，沿斜面向上为y轴，建立平面直角坐标系xOy.

图2 质点受力分析图

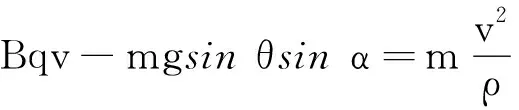
(1)

由于带电质点的速率为

(2)

轨迹的曲率半径为

(3)

把式(2)、(3)代入式(1)得

不同程序中当事人所提供的现有技术证据不尽相同，导致裁决者认识到的专利申请实际上的技术贡献以及对技术细节的理解也不尽相同，对技术方案的最终解释也会产生不可预知的影响。

(4)

整理后得

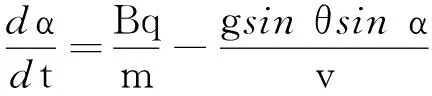
(5)

随着时间推移，式(5)会趋近于零，角α趋于常量，质点达到匀速直线运动状态，则有

Bqv=mgsinθsinα

(6)

(mgsinθ)2=(Bqv)2+(μmgcosθ)2

(7)

联立式(6)、(7)可求得

(8)

(9)

带电质点在切向由牛顿运动第二定律得

(10)

将式(10)两边同乘以dα则有

(11)

将式(5)代入式(11)得

(12)

将式(12)整理后得

(13)

进一步研究发现，式(13)没有解析解.

3 动力学微分方程组

由图2中质点受力分析图，可以写出质点动力学微分方程组如下

(14)

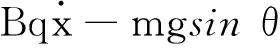
(15)

x(0)=0,y(0)=0,x′(0)=y′(0)=0

(16)

进一步研究发现，式(14)、(15)、(16)没有解析解.

4 数值模拟

由式(8)得

(17)

由式(9)得

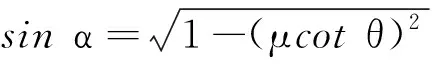
(18)

代值求得

α=arccos(μcotθ)≈1.513 rad

(19)

图3是质点运动轨迹图，可以看出质点振动的幅度越来越小，最终趋近于直线运动，不是圆的渐开线运动;图4是质点速率与夹角α关系图，可以发现质点最终速率趋近于一个定值，速度的方向趋近于不变.

图3 质点运动轨迹图

图4 质点速率与夹角α关系图

图5是质点两个分速度与时间关系图，可以看出它们的振幅越来越小，最终都趋近于匀速直线运动，图6是质点速率与时间关系图，可以看出质点最终速率趋近于某一定值.

图5 质点两个分速度与时间关系图 图6 质点速率与时间关系图

5 结论

通过以上分析不难发现，带电质点运动轨迹最终趋近于匀速直线运动，质点在x轴和y轴方向上的分速度最终都趋近于定值，都是趋近于匀速直线运动，而不是圆的渐开线运动.进一步研究还发现：若μ=0时，带电质点的运动轨迹是一条摆线[2,3]，感兴趣的教师可以自行推证，这里不再赘述.