基于单模态生理信号无监督特征学习的驾驶压力识别
2021-07-26江润强陈兰岚
江润强, 陈兰岚, 谌 鈫
(华东理工大学能源化工过程智能制造教育部重点实验室,上海 200237)
驾驶压力被认为是影响驾驶员意识和行为的主要因素,可能会导致驾驶员在道路上的攻击性和危险行为。如何有效地检测驾驶员的压力状态,提高行车过程中的驾驶意识和驾驶表现,对道路交通以及人身安全具有重要的现实意义[1]。
目前,对于驾驶压力状态的检测方法主要有:主观问卷调查、生理信号分析、驾驶行为检测、视觉与语音信号分析。在不同的检测方法中,由于生理信号能够较好地表征人体的心理与生理信息,具有一定的客观性与实时性,近年来得到了国内外众多学者的关注。与人体压力状态有关的生理信号主要包括脑电(Electroencephalogram, EEG)、心电(Electrocardiogram, ECG)、肌电(Electromyogram, EMG)、皮电(Galvanic Skin Response, GSR)、眼电(Electrooculogram, EOG)等[2]。
文献[3] 采集了眼电、脑电以及肌电3 种生理信号并设计了不同层面的样本熵及复杂度特征,20 个受试者在4 种驾驶状态下的识别准确率为96.5%~99.5%。文献[4]对脑电信号和眼电信号提取出样本熵、近似熵和谱熵并进行了基于熵的特征层面的融合,22 个受试者的平均识别结果为99.1%。文献[5]对皮电、肌电、心电3 种生理信号分别提取出时频域的特征并进行多模态融合,在12 个受试者的3 种驾驶压力负荷下的平均识别结果超过了80%。上述对于驾驶压力疲劳检测的相关研究往往涉及到多个模态的生理信号,一定程度上保证了信息的完整性与丰富性,但在实际的驾驶环境中多电极生理信号的采集会影响驾驶员行车的舒适性,也会导致检测成本的提高。
针对上述问题,本文采用单模态生理信号进行驾驶压力的检测,选取了与压力识别相关性较强的脚部皮电信号[6]。该信号的采集较为方便,可直接放置于驾驶员的鞋垫中,且具有皮肤电导水平和皮肤电导反应的波形特点,可反映驱动人类行为、认知和情绪状态的交感神经活动水平[7]。
此外,传统的对于生理信号的特征提取方法往往需要研究者具有较丰富的先验知识,属于特征工程的范畴。而深度学习作为一种表征学习的方法,具有对输入对象自动进行学习并且提取出相应抽象特征的能力,以此来学习高维数据的低维表示和对高维数据的压缩重构[8]。近年来,许多学者将基于深度学习的特征表示和特征融合应用到脑电等生理信号的处理中。文献[9] 利用深度自编码器进行脑电和眼电特征的融合来展开情感识别的研究。文献[10]运用深度信念网络提取脑电信号的抽象特征进行脑机接口中左右手动作的识别。文献[11]利用卷积神经网络提取出不同导联肌电信号的抽象特征并输入到分类器中进行膝盖位置动作信息的识别。本文构建了基于单模态生理信号无监督特征学习的驾驶压力识别模型,采用一维卷积神经网络构造卷积自编码器提取皮电信号的抽象特征,并借鉴集成学习的思想,提高了驾驶压力识别的准确率与稳定性。
1 方法与模型
本文构建的驾驶压力识别模型如图1 所示。将经过带通滤波处理后的皮电信号数据样本送入卷积自编码器(Convolutional Auto-Encoder, CAE)中进行神经网络参数的训练学习,其中卷积自编码器的编码阶段学习到对应的抽象特征,再将其依次送入支持向量机(Support Vector Machine, SVM)、随机森林(Random Forest, RF)、K 最近邻(K-Nearest Neighbor,KNN)、梯度提升决策树(Gradient Boosting Decision Tree, GBDT) 4 种基分类器进行驾驶压力识别建模。对4 种基分类器的输出采用投票(Voting)策略进行决策级的集成,得到最终的驾驶压力识别结果。

图1 驾驶压力识别模型框架Fig. 1 Framework of driving stress estimation model
1.1 一维卷积自编码器
卷积自编码器包含有编码与解码两个阶段[12]。其中编码阶段主要由输入层、卷积层、池化层(下采样层)、重构层以及全连接层组成;解码阶段主要由重构层、全连接层以及上采样层、反卷积层组成,在编码阶段对脚部皮电的抽象特征进行学习。一维卷积自编码器示意图如图2 所示,其中dim 为抽象特征的维数。

图2 一维卷积自编码器示意图Fig. 2 Schematic diagram of one dimensional convolution auto-encoder
1.1.1 编码阶段
(1)卷积层。卷积层由若干个卷积核对输入进行卷积运算得到的特征图组成,以此来提取输入对象的局部特征[13]。卷积层的数学原理为
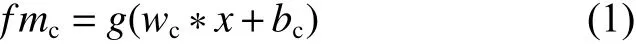
其中:fmc表示卷积作用后的特征图;wc与bc分别表示卷积核对应的权重与偏置;*表示对应的卷积运算;g表示相应的激活函数。卷积的边界补零填充主要是为了保持卷积后数据的尺寸不变。
(2)池化层。池化层又称为下采样层,其作用相当于对卷积层提取的抽象特征进行选择,以此达到特征的降维[14]。本文选用的最大池化层的数学原理为

其中:pmp表示经过最大池化作用后的特征图。
(3)重构层与全连接层。重构层将pmp转化为一维列向量,然后再输入到全连接层编码得到抽象特征,其中全连接层神经元的个数为压缩后抽象特征的维数。其数学原理为

其中:v表示重构后的列向量;c表示编码得到的抽象特征;wf和bf分别表示全连接层所对应的权重与偏置;·表示点乘运算。
1.1.2 解码阶段
(1)全连接层与重构层。抽象特征解码的过程是编码的逆过程,需要通过全连接层将抽象特征转化为列向量,然后再通过重构层将其转化为对应尺度的特征图。其数学原理为

其中:vd表示解码阶段的列向量;wdf表示解码阶段全连接层的权重,同时解码阶段的重构建立在编码得到的抽象特征c的基础上,为保证信息的完整性,解码阶段的全连接层不存在对应的偏置[15];rm为解码阶段重构后的特征图。
(2)上采样层与反卷积。上采样层可以看作反池化的过程,主要用于特征子图的维度扩充。扩充后的特征子图再经过反卷积作用得到对应的重构信号。其数学原理为

其中:fmup表示上采样后的特征子图; ° 表示反卷积运算;wdc与bdc分别表示反卷积的权重与偏置,其维度大小分别为对应卷积阶段权重与偏置矩阵的转置;y为解码阶段反卷积得到的重构信号[16]。
1.1.3 网络激活函数 本文中除解码阶段最后反卷积层的输出为Sigmoid 激活函数外,网络架构的其余卷积与反卷积层激活函数均采用修正线性(Rectified Linear Unit, Relu)激活函数。
Relu 激活函数:

Sigmoid 激活函数:

1.1.4 网络损失函数 自编码器的损失函数依据原始输入与重构输入之间的偏差最小化,本文采用的损失函数为平均绝对误差,计算公式如下:

其中:N为样本数目;x(i)为原始信号的第i个样本;y(i)为原始信号第i个样本对应的重构信号。
1.1.5 卷积自编码器结构设计 在反复实验的基础上,本文选取2 个卷积层和2 个池化层作为卷积自编码的编码阶段,其中全连接层的神经元个数作为抽象特征的维度;选取3 个反卷积层和2 个上采样层作为卷积自编码的解码阶段。具体的参数设置见表1,表中dim 为全连接层神经元的个数,也即抽象特征的维数。

表1 卷积自编码器的超参数Table 1 Hyperparameters of the convolutional auto-encoder
1.2 集成学习
集成学习是指融合多个学习器或者模型来完成某个具体的学习任务,分为同质集成学习与异质集成学习[17]。本文对分类器的集成建立在不同基分类器基础之上,属于异质集成学习的范畴,并从硬投票和软投票两个角度分别进行集成。
(1) 硬投票是对不同基分类器的输出类别采用少数服从多数的投票原则确定出对应的预测标签,其局限性在于未考虑到类别标签输出概率的累加性。
(2) 软投票也称为加权投票法,集成模型的输出为各个基分类器预测概率的加权平均,数学表达式为

其中:n表示分类器的个数;wi表示第i个分类器的权重;yi表示第i个基分类器的概率输出值;Y表示加权平均后的概率输出值。本文中n=4,同时各个基分类器的权重wi保持一致,均设定为1。
本文针对硬投票存在的问题,取不同基分类器模型对样本预测概率的平均值作为标准,从中选取概率最高的所属类别作为最终的预测标签。
1.3 分类模型的评价
为充分评估分类模型的有效性,采用精确率(Precision)、召回率(Recall)、准确率(Accuracy)和F1分数(F1) 4 个评估指标定量地分析评价模型[18]。评估指标定义如下:

其中:TP 表示模型预测为正类的正样本;FP 表示模型预测为正类的负样本;TN 表示模型预测为负类的负样本;FN 表示模型预测为负类的正样本。
2 实验结果分析
2.1 实验数据
实验数据选用美国PhysioBank 公开的MITdrivedb 数据集,该数据集包含了9 名驾驶员17 次在波士顿特定路段真实驾驶环境下多源生理信号的驾驶记录,其中3 次驾驶过程的数据存在一定的缺失,故本文采用了14 次驾驶过程的完整数据。原实验设计者采集了多种外周生理信号,比如手部皮电(Hand Galvanic Skin Response, HGSR)、 脚 部 皮 电(Foot Galvanic Skin Response, FGSR)、心电(ECG)、呼吸(Respiration, RESP)。实验设定了车库休息、高速公路、市区道路3 种驾驶情景,以此表征低、中、高压3 种驾驶状态。每名受试者的驾驶过程为休息-高速-市区3 种驾驶状态循环往复,实验流程如图3 所示。整个实验过程中还进行了视频图像分析与问卷调查的客观分析,以此来佐证实验设计的合理性和有效性[19]。
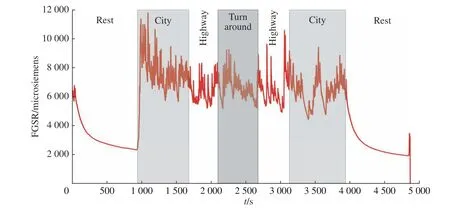
图3 数据集实验流程Fig. 3 Experiment flow of data set
本文采用FGSR 信号进行实验,其采样频率为31 Hz。原始采集的FGSR 信号经过缺失值处理及带通滤波后,从每次驾驶过程的低、中、高压3 种状态中分别提取出10 min 信号进行分析,共获取30 min的驾驶片段。再利用滑动窗口进行数据分段,固定窗口的大小为100 s,滑动步幅为10 s,这样每个驾驶周期共产生126 个数据样本,每种驾驶状态下各42 个,其中每个样本的数据长度为31×100=3 100。14 次驾驶过程共可获得1 764 个数据样本。
实验环境:软件环境为Matlab2018 和Anaconda3下的Python3.7,其中Matlab 主要用于原始信号的提取、样本的划分。Python 的编程环境通过Keras 搭建基于一维卷积自编码神经网络的特征学习框架,通过Sklearn 库完成不同基分类器的识别与参数的寻优,以及特征学习算法的比较与特征可视化。
2.2 抽象特征的学习效果分析
2.2.1 数据预处理及模型训练 为保证一维卷积无监督自编码器损失函数的收敛性以及网络的训练时间成本,对原始数据样本按列进行0-1 归一化处理。将14 次驾驶过程的全部数据样本随机打乱后,其中的90%作为训练集、其余的10%作为验证集进行卷积自编码器网络参数的训练学习。选取Adam 优化器,每个批量大小为40 个样本,Epoch 的数目为80。模型的训练过程如图4 所示。从图4 可以看出,当Epoch 达到80 时,验证集与测试集的误差损失基本一致,模型不存在过拟合。

图4 一维卷积自编码器的训练Fig. 4 Training of one dimensional convolutional auto-encoder
2.2.2 抽象特征的可视化 对于学习到的抽象特征,通过流行学习层面的T-SNE (T-Distributed Stochastic Neighbor Embedding)进行特征的可视化。T-SNE 能够将样本之间的相似度关系在嵌入空间(二维空间)转化为概率分布,这使得T-SNE 的数据可视化可以关注数据样本的局部与全局分布[20]。本文选取了3 个个体进行抽象特征的可视化展示,如图5 所示。从图5 可以看出,卷积自编码器提取的抽象特征能够比较明显地区分出3 种不同的驾驶状态。

图5 抽象特征的可视化Fig. 5 Visualization of abstract features
2.2.3 抽象特征对于路况的表征能力 为进一步分析提取的抽象特征对不同驾驶状况的表征能力,对14 次驾驶过程分别进行驾驶压力的识别,选取径向基核函数的SVM 作为基分类器,将区别3 种路况的三分类问题转化为3 个二分类问题,并计算出每次驾驶识别结果对应的TP 与FP,其中14 次驾驶过程平均识别结果的ROC 曲线以及ROC 曲线下的面积如图6 所示。
从图6 可以看出,对于14 次驾驶过程而言,卷积自编码器提取的抽象特征对车库休息状态的平均识别结果最好,ROC 曲线下的面积为0.97;其次为城市路况阶段,ROC 曲线下的面积为0.96;高速路况阶段ROC 曲线下的面积为0.95。

图6 不同路况下的ROC 曲线以及AUCFig. 6 ROC curves and AUC under different road conditions
2.2.4 特征学习算法的比较 为分析深度学习层面特征学习的有效性,选取多维缩放(Multidimensional Scaling, MDS)[21]、主成分分析(Principal Components Analysis, PCA)[22]、稀疏随机映射(Sparse Random Projection, SRP)[23]3 种基于矩阵映射的传统特征学习算法与卷积自编码器(CAE)进行比较。对不同的特征学习算法依次设置了6 个特征维度进行特征学习,用于特征学习评估的基分类模型均为径向基核函数的SVM。对于每次驾驶过程的126 个数据样本,选取70%的样本用于训练,30%的样本用于测试,14 次驾驶过程通过不同的特征学习方式所得的驾驶压力识别结果如图7 所示。对于本数据集而言,卷积自编码提取的抽象特征在维度不小于8 时优于传统特征学习算法,这表明基于深度学习的特征学习在调整好其超参数的基础上可以替代传统特征学习算法,且无需任何与生理信号相关的先验知识。
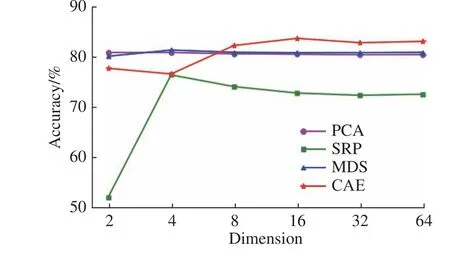
图7 不同维度下的特征学习算法比较Fig. 7 Comparison of feature learning algorithms under different dimensions
2.3 驾驶压力识别效果分析
为提高决策级层面识别结果的稳定性与准确率,选取KNN、RF、GBDT、SVM 作为基分类器,同时采用软投票与硬投票的集成学习策略。其中,对于不同维度下的样本空间,数据划分方式与2.2.4 节一致,基分类器的相关参数采用4 折交叉验证的方式进行网格化参数搜索,其参数的搜索范围如表2 所示。

表2 基分类器及参数设置Table 2 Base classifiers and parameter setting
表3 示出了不同基分类器不同维度下14 次驾驶记录的压力识别平均准确率。可以看出在同一维度下,不同基分类器的识别结果存在一定的差异。整体而言KNN 的表现相对较好,其中,在维度为4、8、16 时,KNN 与SVM 的识别结果均达到了90%以上的水平。KNN 在维度为8 时达到了单分类器的最佳识别结果(92.519%,表中黑体)。

表3 不同基分类器不同维度下的识别结果Table 3 Recognition results under different dimensions of different base classifiers
表4 示出了特征维度为8 时集成模型的准确率、精确率、召回率、F1,可见两种集成方法均对驾驶压力的识别有一定的提升作用,其中软投票要优于硬投票的识别效果(表中黑体)。
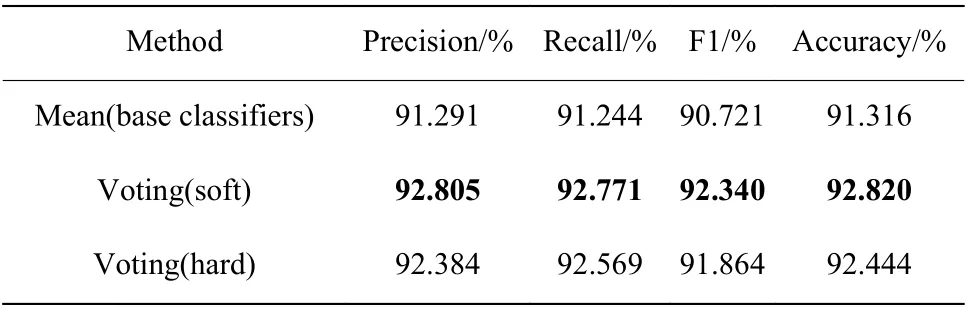
表4 基分类器的投票集成Table 4 Voting integration of base classifiers
2.4 同类结果的比较分析
与同样采用MIT-drivedb 数据集的传统手工特征方法进行比较,比较结果如表5 所示。文献[19]为本数据集的原始参考文献,实验设计者对心电、肌电、皮电、呼吸4 种模态生理信号设计了22 维的手工特征,3 种状态的识别准确率为97.40%,但该研究样本划分时间长度为5 min,实时性较差,同时涉及到多个模态的信号。文献[19]、文献[6]中曾提及与驾驶压力状态最为相关的是皮电与心电两个单模态,本文对单模态的分析结果进行进一步的对比。文献[24]采用单模态的心电信号作为研究对象,对心电信号进行心率变异性(Heart Rate Variablity, HRV)检测,提取出相应的时域、频域、时频域以及非线性特征,驾驶压力识别的平均准确率为83.00%。文献[25]结合心电信号的生理波形特点提取其RR 间隔、QT 间隔以及EDR 3 种类型的手工特征,个体识别平均结果为98.6%,但该研究仅区分了两种驾驶压力状态。文献[6]采用单模态脚部皮电信号作为研究对象,样本划分方式与本文相同,提取了18 个脚部皮电的手工特征,采用KNN 作为分类器,3 种状态的识别准确率为88.91%。文献[26]中样本划分长度为5 min,设计并提取了皮电信号的相应手工特征,采用线性判别分析(Linear Discriminant Analysis, LDA)作为分类器,3 种状态的识别准确率为81.82%。综合研究结果表明,本文在单模态生理信号上利用基于深度学习的无监督特征学习方法,取得了较好的识别效果。

表5 同类研究的对比Table 5 Comparison of similar studies
3 结束语
本文采用单模态的脚部皮电信号构建驾驶压力识别模型,采用一维卷积自编码器进行抽象特征学习,并应用了决策级的集成学习策略。实验结果表明,脚部皮电与驾驶压力的关联度较高,所提取的抽象特征具有较好的表征能力,集成学习有助于提高模型的识别准确率。本文的驾驶压力识别是针对单个个体的识别,没有涉及到跨个体驾驶压力的识别,下一步的研究方向可以借鉴迁移学习的域自适应,构建深度迁移模型研究跨个体的驾驶压力识别。
