隧道掘进对近接垂直交叉隧道的三维有限元分析
2021-07-25赵俞成艾兵兵刘东宋强冯伟艾志伟
赵俞成,艾兵兵,刘东,宋强,冯伟,艾志伟
(1.浙江大学 滨海和城市岩土工程研究中心,浙江 杭州 310058;2.中铁二局集团有限公司杭州地铁项目经理部,浙江杭州 310058;3.杭州市地铁集团有限责任公司,浙江 杭州 310058)
近几十年来,研究土体-隧道相互作用的方法多种多样,包括现场监测、模型试验、经验/分析方法和数值模拟[1-5],然而,大多数研究集中在平行隧道和背驮式隧道,对垂直交叉隧道研究较少.此外,大多数研究使用简单的弹性-理想塑性本构模型对隧道相互作用进行数值分析[6-9],没有考虑由于应力增加导致土体剪切模量的改变以及刚度的变化.基于速率型张量函数建立的亚塑性模型能够更好地描述土体复杂的本构特性[10-11].因此,有必要应用砂土的亚塑性本构模型研究垂直交叉隧道施工过程对邻近既有隧道的影响.
关于垂直交叉隧道的研究有限.Kim 等[12]在1g条件下进行了模型试验,研究了粘土地层中新建隧道对既有隧道的影响.在垂直交叉隧道中,衬砌变形和弯矩在隧道开挖的初始阶段有明显的变化.由于试验是在1g 的条件下进行的,原型尺度下的实际应力状态不能被复制,因此不能很好地反映土的剪胀行为.Liu 等[13]采用三维有限元分析方法,研究了在新建隧道上下垂直施工时,隧道开挖对既有隧道的影响.衬砌在拱脚处受拉,而在拱顶和仰拱处受压.但该项研究未对既有隧道附近土体的应力传递机理进行研究.Ng 等[14]在60g 条件下开展离心机模型试验,并基于砂土的亚塑性本构模型采用有限元分析方法,研究了隧道竖直间距与直径之比(P/D)对垂直交叉隧道相互作用的影响.当P/D 较小时,既有隧道中心线处的沉降较大.但该研究未考虑垂直交叉隧道的施工顺序对既有隧道的影响.Wang 等[15]开展了两组离心机模型试验,研究了干砂中现有隧道的形状(圆形和马蹄形)对垂直交叉隧道相互作用的影响,并使用PLAXIS 3D 进行三维数值反分析,但未考虑新建隧道上穿的情况.
目前,鲜有研究涉及砂土中垂直交叉隧道的施工顺序对既有隧道的影响.不同的隧道施工顺序引起不同的地应力变化,从而引发不同的应力传递机制.这导致了不同的地表沉降和变形,从而引起隧道衬砌产生不同的弯矩.因此,有必要研究施工顺序对邻近既有隧道的影响.本研究采用三维有限元分析方法,研究了施工顺序对垂直交叉隧道的影响.数值分析采用砂土的亚塑性本构模型,考虑了土体的小应变刚度.此外,将计算结果与只模拟体积损失(即不考虑重量损失的影响)的情况进行比较,以证明质量损失对不同施工顺序的显著影响.对既有隧道的地面沉降、变形和位移、弯矩和轴向力的影响进行了研究.同时对土的应力传递机理进行了分析,并将其应用于土的力学行为研究.
1 数值模型
1.1 有限元网格和边界条件
图1 和图2 显示了针对工况S1 和S2 的平面图和正视图.工况S1 指在既有隧道上方新建隧道的情况,而工况S2 指在既有隧道下方新建隧道的情况.新建和既有隧道均为盾构隧道,长度和直径分别为100 m 和5 m,隧道衬砌厚度为0.2 m.根据《公路隧道设计规范》(JTG D70-2014),本研究假设隧道衬砌厚度为0.2 m.矿柱宽径比P/D 为1.0,其中矿柱宽度定义为两隧道衬砌之间的最短距离.假设C/D 为8.5,即距离地面42.5 m.利用有限元程序ABAQUS[16]对既有隧道上方和下方隧道开挖进行了模拟.
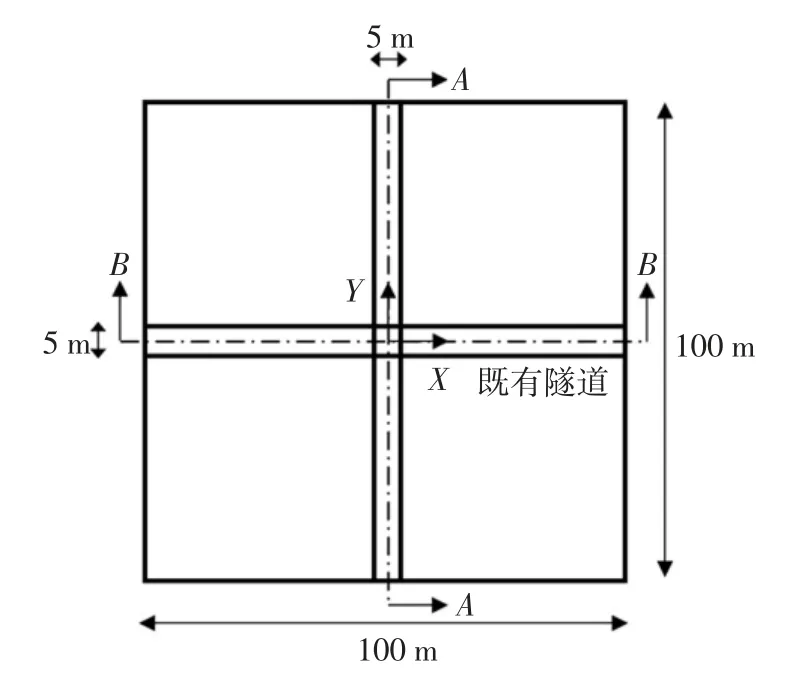
图1 隧道S1、S2 平面图Fig.1 Plane view for S1 and S2
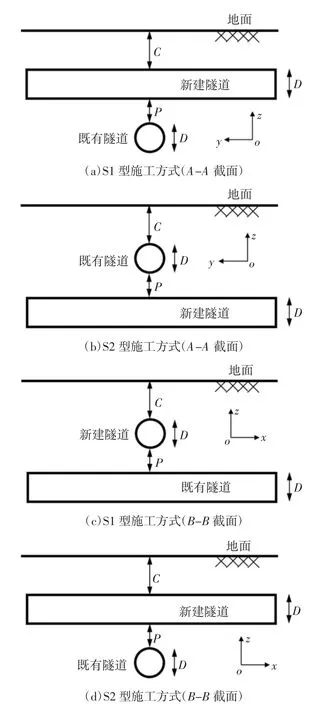
图2 S1、S2 两种施工方式立面图(示意图)Fig.2 Elevation view for S1 and S2(schematic diagram)
图3 为工况S1 的三维有限元网格,新隧道轴线位于距地面45 m 处,距既有隧道轴线10 m 处.工况S2 的网格与S1 相似,新隧道和既有隧道的位置与S1 正好相反.此外,还分析了另外两种无既有隧道工况(对应S1 和S2),以比较工况S1、S2 的地表沉降槽情况.上述6 种工况参数见表1.网格尺寸为100 m(长)×100 m(宽)×100 m(高),由22 556 个元素和26 341 个节点组成.采用四节点壳单元对隧道衬砌进行建模,采用八节点实体单元对土体进行建模.边界条件为底部及四个垂直面固定,从而限制底部和四个垂直面在任何方向的运动.

图3 S1 有限元网格Fig.3 Finite element mesh for S1
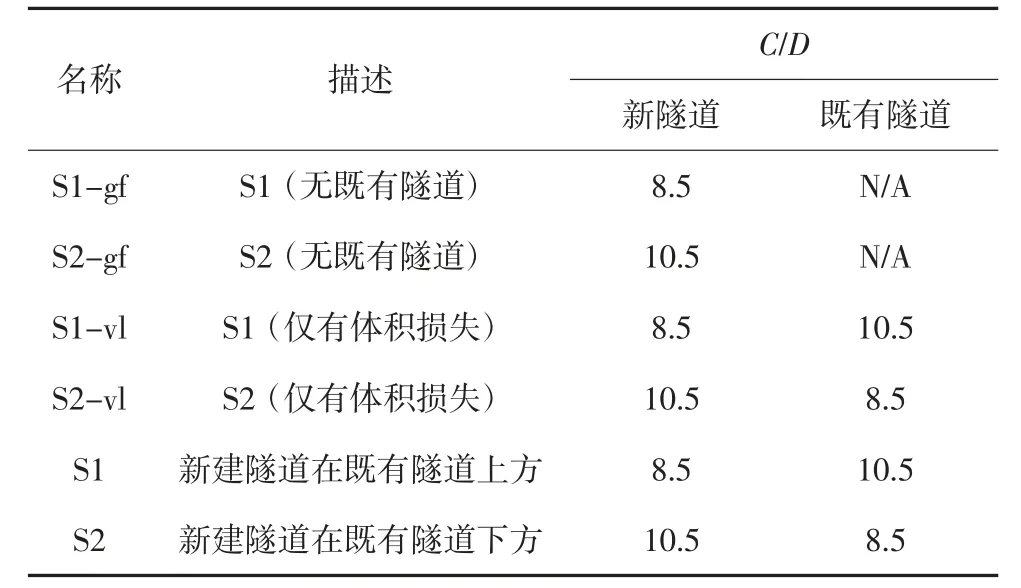
表1 数值模拟方案Tab.1 Numerical analysis program
1.2 本构模型和模型参数
亚塑性模型描述颗粒材料非线性响应[17].该模型由单个非线性张量方程表示,建立了应力速率张量()与应变速率张量()的关系如下:

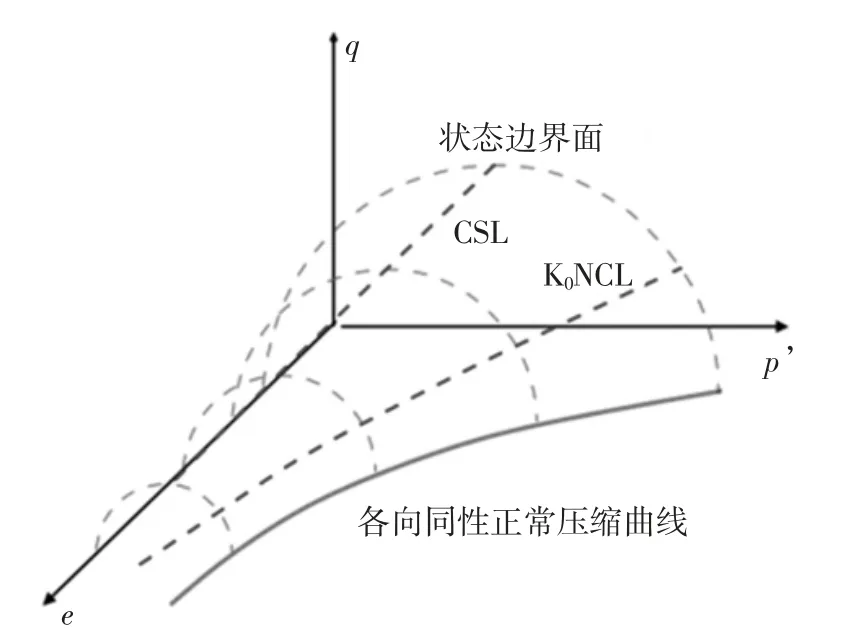
图4 亚塑性模型的状态边界面图解Fig.4 Illustration of state boundary surface in hypoplastic model

式中:hs和n 为曲线拟合的两个参数.ei、ed和ec分别为各向同性压缩下的最大孔隙比、最小孔隙比和临界状态孔隙比.eio、edo和eco分别表示零围压条件下对应的最大、最小和临界状态孔隙比.
式(1)中的本构张量L 表示如下:

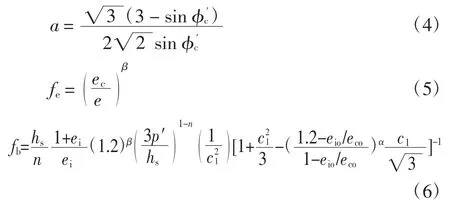
参数α 与土体膨胀有关,β 控制土体刚度处于较大应变水平(剪切应变>1%).在较大的应变下,较大的β 与较硬的土体响应有关.参数c1是的函数,表示为:
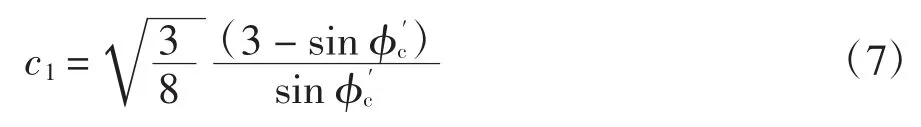
式(1)中本构张量N 表述如下:


Niemunis 和Herle[18]为了考虑小应变下土体刚度的应变依赖性和路径依赖性,进一步改进了基本的HP 模型,将粒间应变的概念纳入模型.还需要5 个附加参数(mR,mT,R,βr,χ).在5 个参数中,mR和mT分别在180 和90 应变路径反转时控制初始剪切模量,R 为弹性应变范围,βr和χ 是用应变定义刚度退化率的参数.
通过ABAQUS 的用户材料子程序(User-defined Material Mechanical Behavior,简称UMAT)接口程序对亚塑性模型进行数值实现.本研究中采用Masin[19]开发的UMAT 程序.该程序利用与有限元相结合的基于矩阵广义逆一致性切向模量矩阵,形成了通过UMAT 接口实现亚塑性模型的数值方案.
本研究中,假设土体为丰浦砂,表2 为丰浦砂亚塑性模型参数[20].混凝土隧道衬砌采用线弹性材料.考虑到衬砌接头对衬砌结构刚度的影响,将衬砌管片结构刚度折减0.15,杨氏模量为30 GPa(折减后),泊松比为0.25[21].隧道衬砌的有效单位重量为25 kN/m3[5].
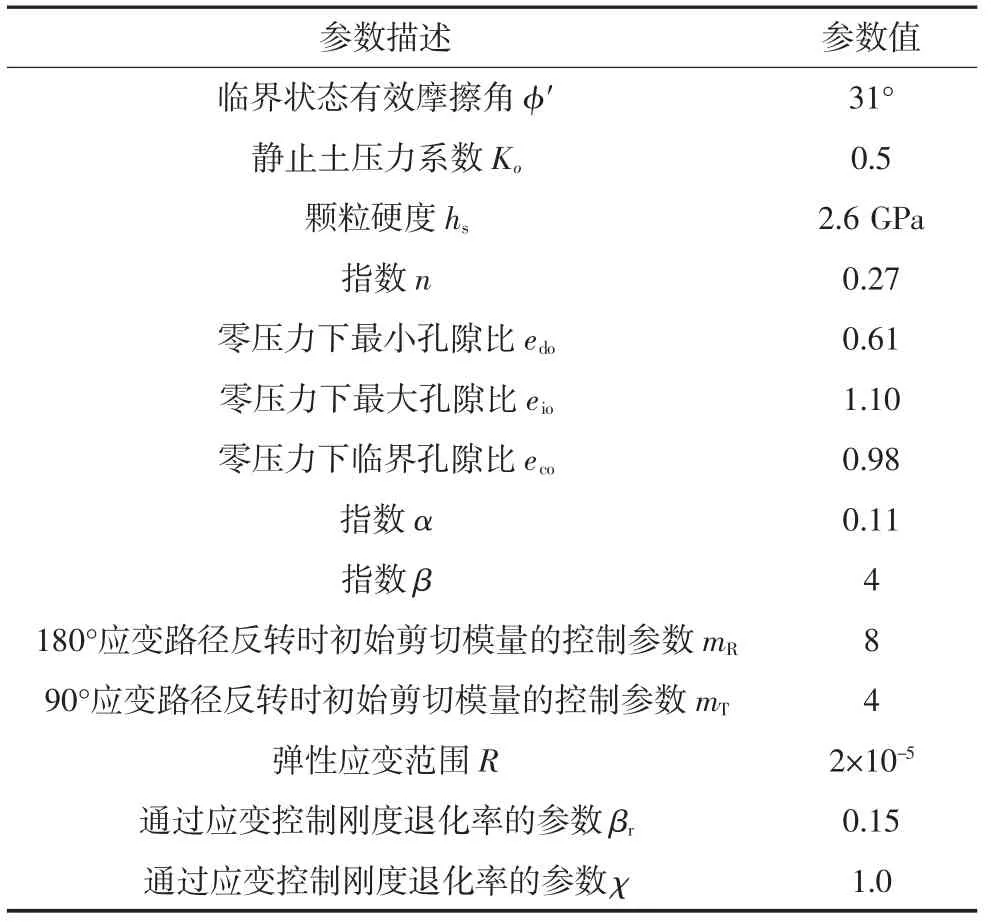
表2 土体参数Tab.2 Soil parameters
1.3 数值模拟方案
如前述表1 所示,共分析了6 种工况.首先进行了S1 和S2 两种不同施工顺序的分析,研究了新建隧道对地面和既有隧道的影响.为了研究既有隧道在新建隧道开挖下对地面沉降的影响,增加了仅有隧道开挖的工况(无既有隧道,对应于S1 和S2).在只模拟体积损失的情况下进行了另外两种工况,以证明建模质量损失对不同施工顺序的显著影响,即在隧道衬砌周围开挖只模拟2%的体积损失,而没有开挖隧道衬砌内部的土.根据北京、上海、武汉、深圳等地盾构隧道施工引起的地表损失率数据,对71 组数据进行统计分析.结果表明,地表损失率在0.2%~3.01%之间[22].因此,本研究假设2%的体积损失是合理的.本研究采用的模拟隧道开挖的数值模型已被广泛应用,并得到了前人研究的验证[23-25].
图5 为隧道开挖过程.在盾构掘进过程中,开挖面支护力沿深度线性变化,大小与侧向土压力相同[26],注浆压力为0.2 MPa[27].新建隧道(长100 m)分为80段,每段挖土1.25 m.为了既能反映盾构推进过程及其对既有隧道的影响,又能满足计算量要求,避免尺寸效应及边界带来的计算误差,新建隧道开挖时首先会挖去8 段,共计挖土10 m.隧道开挖是通过移除位于开挖区域的土体来模拟的,即通过使土体单元失活来开挖隧道衬砌内部和衬砌周围的土体.每一个开挖步包含两个分析步:第一步为应力释放,即刚度折减过程,在刚度折减的同时,在开挖面处施加支护力.第二步开挖土体然后生成衬砌,土体与衬砌单元的接触设为绑定接触(*interaction,tie adjusted surface).绑定接触可以实现两个面之间没有连接关系,从这个分析步开始才绑定在一起.在只考虑体积损失的情况下,仅在衬砌周围开挖土体.衬砌会在重力作用与土层接触,进行应力传递.如图5 所示,土体与隧道外径之间的间隙相当于2%的体积损失.这样简化了隧道衬砌周围2%体积损失的位移控制方法.模拟重量损失时,将隧道内部的土体单元全部失活.隧道开挖过程可视为盾构掘进.这种建模技术可以模拟隧道施工过程中的重量损失和体积损失.在每个掘进阶段,隧道工作面不允许发生水平位移.

图5 数值模拟过程示意图Fig.5 Schematic diagram of numerical modelling procedure
2 结果分析
2.1 地表沉降
图6 为开挖结束时沿B-B 段计算出的地表横向沉降槽.其中,图6 的实测值是Ng 等[24]在60g 条件下离心机模型试验测得的结果,试验中新建隧道在既有隧道下方(C/D=2;P/D=0.5).对于双隧道的工况(S1 和S2),工况S1 的最大地表沉降大于工况S2,其中S1 和S2 的最大地表沉降分别为6.6 mm 和6.2 mm.这是因为S1 的新隧道C/D 比S2 的小.对比工况S2 和实测值,沉降量随中心线偏移量的变化均呈现中间大两头小的规律,最大地表沉降相差4 mm.这是由于Ng 等[24]的试验条件P/D=0.5,工况S2 的P/D=1,根据Ng 等[14]论文的结果,P/D 较小时,既有隧道中心线处的沉降较大.因此,模型预测结果较为合理.图中S1-gf 和S2-gf 为无既有隧道工况,地表最大沉降量(即S1-gf 和S2-gf)分别大于相应的双隧道条件(即S1 和S2).这是由于现有隧道的存在使土体变硬,导致S1 和S2 两种情况下最大地表沉降降低了约14%.
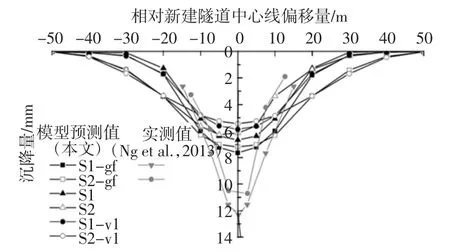
图6 隧道地表横向沉降槽的对比Fig.6 Comparison of transverse ground surface settlement troughs
另一方面,仅有体积损失工况(S1-vl 和S2-vl)的地表沉降均小于双隧道和无既有隧道的沉降.S1-vl 和S2-vl 最大地表沉降分别为5.8 mm 和5.4 mm.也就是说,S1-vl 和S2-vl 的地表最大沉降量分别比S1 和S2 小12%和13%.可以解释为隧道衬砌内土体质量的去除引起了新隧道周围总应力的变化.与只考虑体积损失影响而不考虑质量损失影响的S1-vl 和S2-vl 相比,S1 和S2 的新隧道周围出现较大的应力释放.因此,地表沉降小于S1 和S2 两种情况.
2.2 隧道纵向沉降
图7 为既有隧道沿B-B 截面(见图1)的纵向沉降分布,不同推进阶段的纵向沉降量通过y/D 比值表示.y/D 代表隧道掌子面与既有隧道中心线(B-B截面)的距离与隧道直径的比值.随着y/D 比值的增加,工况S1 和S1-vl 既有隧道的轴线部分向上位移(即隆起),工况S2 和S2-vl 向下位移(即沉降).这是因为隧道开挖会减少既有隧道的应力,导致既有隧道向新建隧道移动.S1 处既有隧道最大沉降量为9 mm,S2 处最大沉降量为16 mm.S1 和S2 沉降差分别为11.6 mm 和11.8 mm.S1 和S2 差异沉降分别相当于1 ∶2 800 和1 ∶2 400 的梯度.S2 沉降差和梯度略大于S1,这是由于应力释放的作用更大.S1-vl 和S2-vl 的差异沉降量小于S1 和S2.S1-vl 和S2-vl 的差异沉降分别比S1 和S2 小54%和53%.由于没有减少衬砌内土体质量,导致S1-vl 和S2-vl 的应力释放效果小于S1 和S2.
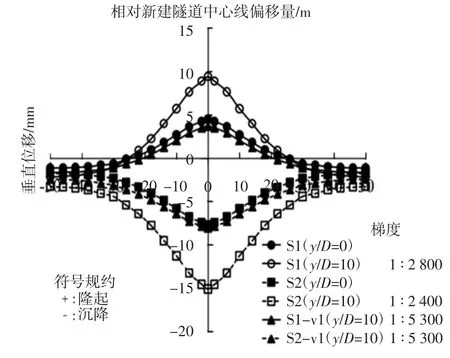
图7 隧道纵向垂直位移的比较Fig.7 Comparison of longitudinal tunnel vertical displacement
图8 为在工况S2 中不同推进阶段(y/D 表示)竖向位移U3 的云图.为了便于观察,只截取了靠近隧道的局部区域.随着新建隧道的不断推进,工况S2既有隧道及周围土体的竖向位移不断增大,新建隧道下部结构、土体均产生不同程度的“上浮”,最大值位于隧道结构的临空面.

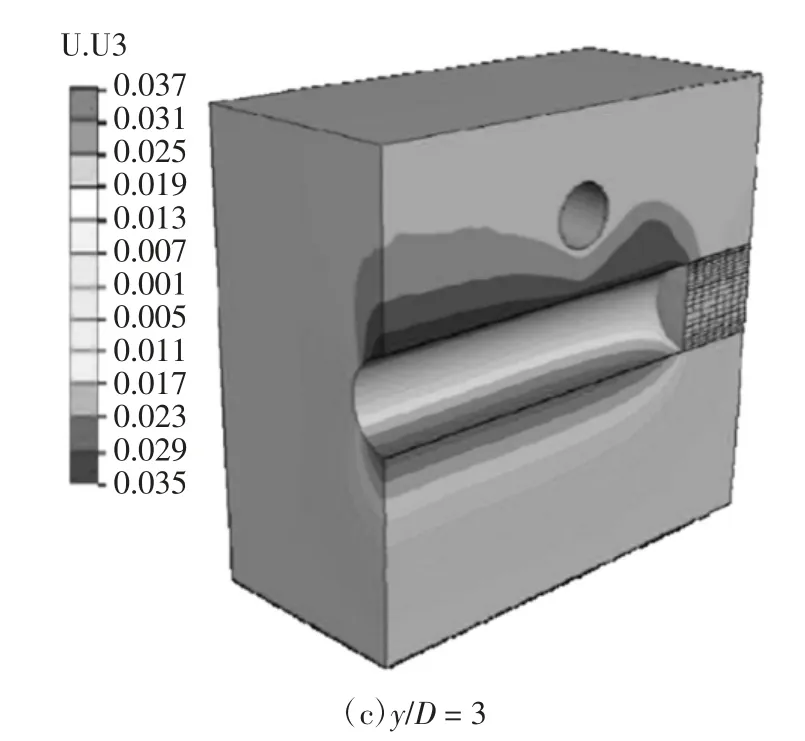
图8 隧道竖向位移云图(m)Fig.8 Contours of vertical displacement around tunnel(m)
2.3 既有隧道的位移和变形
图9 为既有隧道在A-A 截面不同推进阶段(y/D 表示)的位移和变形形态.随着y/D 比值的增加,工况S1 既有隧道发生了向上位移(即隆起),工况S2既有隧道发生了向下位移(即沉降).这是因为隧道开挖会减小既有隧道的应力,从而导致既有隧道向新建隧道移动.S1 和S2 工况下,既有隧道在开挖结束时的最大向上和向下垂直位移分别约为9.4 mm和15.0 mm(即在y/D=10 处).工况S2 的最大向下垂直位移比S1 最大向上位移大60%.这是因为工况S1 中上覆土体压力阻碍了既有隧道的位移,导致既有隧道向上位移较小(见图7).另一方面,工况S2 的向下位移是由仰拱处的应力降低和既有隧道上方土体压力共同作用的结果.当隧道掌子面y/D=-1 时,既有隧道向新隧道掌子面位移,当隧道掌子面通过监测断面后,横向水平位移回到原来的位置.在隧道施工过程中,由于应力释放的作用,既有隧道在掘进过程中往往向开挖掌子面y 方向移动.

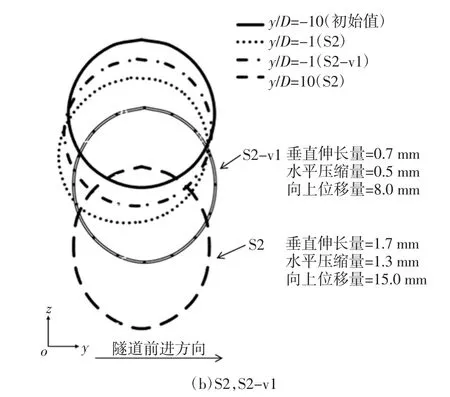
图9 既有隧道的位移和变形(不按比例)Fig.9 Displacement and deformation of the existing tunnel(not to scale)
由于应力释放作用,随着y/D 的增大,水平直径减小(即压缩),垂直直径增大(即拉长).工况S1 的变形在伸长和压缩两方面均略小于S2,S2 既有隧道的垂直延伸和水平压缩分别比S1 大6%和9%.S1和S2 工况下既有隧道的竖向伸长主要是隧道顶部衬砌变形引起的.通过考虑隧道周围的正应力变化导致隧道衬砌产生弯矩,进一步验证了这一点.在开挖完成时(即y/D=10 时),S1 和S2 的垂直伸长量分别比水平压缩量大约33%和54%.另一方面,S1-vl和S2-vl 两种情况下,各既有隧道的竖向位移和变形均小于S1 和S2 两种情况.S1-vl 组和S2-vl 组的上下垂直位移分别比S1 组和S2 组小61%和47%.这是由于与S1 和S2 相比,S1-vl 和S2-vl 没有减少衬砌内土体质量,导致应力释放更小.与S1 和S2 类似,S2-vl 的向下垂直位移大于S1-vl 的向上位移,这是因为减重的影响会引起新隧道周围总应力的变化.随后,当新隧道穿越既有隧道时,既有隧道会因减重而产生额外的应力降低.S1-vl 和S2-vl 隧道变形分别小于S1 和S2 的变形,S1-vl 和S2-vl 的垂直伸长量分别比S1 和S2 小56%和59%.与S1 和S2相似,S2-vl 的变形大于S1-vl.这是因为S2-vl 的拱顶最大弯矩远大于S1-vl.
2.4 既有隧道的弯矩
图10(a)和10(b)为开挖完成时既有隧道衬砌沿A-A 截面的横向弯矩分布.正弯矩表示既有隧道向外变形,负弯矩表示现有隧道向内变形.

图10 新隧道开挖导致的既有隧道衬砌上产生的附加横向弯矩(MN·m)Fig.10 Transverse bending moments(MN·m)induced on lining of existing tunnel at the end of tunnel excavation
如图10(a)和10(b)所示,S1 和S1-vl 最大横向弯矩发生在拱顶,S2 和S2-vl 最大横向弯矩发生在拱底,在S1、S2、S1-vl 和S2-vl 四种工况,最小弯矩均出现在起拱线上.工况S1 最大和最小横向弯矩略小于工况S2.
另一方面,S1-vl 和S2-vl 的最大横向弯矩分别小于S1 和S2.S1-vl 和S2-vl 中既有隧道的垂直位移和变形情况下小于S1 和S2(见图9),S2-vl 最大弯矩大于S1-vl,S2-vl 向下的垂直位移大于S1-vl向上的垂直位移(见图9).图11 为既有隧道衬砌所受纵向弯矩沿B-B 截面分布情况,不同推进阶段的弯矩分布以y/D 比值表示.既有隧道衬砌所受弯矩利用弹性梁理论推导得:
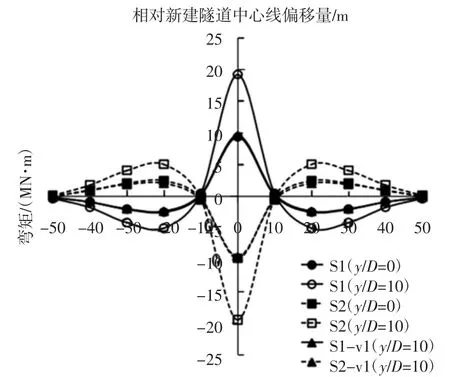
图11 既有隧道衬砌(B-B)附加横向弯矩(MN·m)Fig.11 Transverse bending moments of existing tunnel lining(B-B)(MN·m)

式中:δ(x)是既有隧道衬砌变形;Ep和Ip分别是隧道的杨氏模量和惯性矩.随着掌子面推进,S1 和S2 的弯矩均增大,既有隧道分别向上运动(即隆起)和向下运动(即沉降)(见图7).这导致既有隧道中段出现最大正弯矩和最大负弯矩.S1 的最大弯矩为19 MN·m,小于S2 的弯矩20 MN·m.这是因为S1 的应力比降幅小于S2.另一方面,S1-vl 和S2-vl 的最大弯矩分别比S1 和S2 小47%和50%.与S1 和S2 相比,S1-vl 和S2-vl 的弯矩较小,这是由于S1-vl 和S2-vl的隧道位移较小.此外,S1-vl 和S2-vl 的应力降低幅度小于S1 和S2.
2.5 既有隧道衬砌轴向力
图12(a)(b)分别为S1、S1-vl、S2、S2-vl 开挖完成时既有隧道衬砌沿A-A 段的环向力和纵向轴向力.由图12(a)可知,对于工况S1 和S2,最大的环向力都在拱脚处,最小的环向力在拱顶和拱脚.最大和最小轴力分别为372 kN/m 和197 kN/m.对于工况S1 来说,拱脚以上的环向力大于拱脚以下的环向力,从而导致既有隧道的隆起.相反,在工况S2 中,拱脚以下的环向力大于拱脚以上的环向力,导致既有隧道的沉降.S1-vl 和S2-vl 的环向力分别小于S1和S2.这是由于S1-vl 和S2-vl 的隧道变形分别小于S1 和S2(见图9),且S1-vl 和S2-vl 的应力降低量分别小于S1 和S2(见图13).
从图12(b)可看出,最大纵向轴力分别出现在工况S1 的拱顶处和工况S2 的拱底处,而最小轴力出现在工况S1 的拱底处和工况S2 的拱顶处.这是由于S1 拱顶和S2 拱底附近的应力释放.在S1 和S2两种工况下,衬砌所承受的最大轴力分别为579 kN/m 和584 kN/m.S1-vl 和S2-vl 的轴力大小分别小于S1 和S2.这是由于S1-vl 和S2-vl 的隧道变形要小于S1 和S2(见图9),且S1-vl 和S2-vl 的隧道应力降低量小于S1 和S2.

图12 既有隧道衬砌环向力和纵向轴力(kN/m)Fig.12 Hoop force and longitudinal axial force of existing tunnel linning(kN/m)
2.6 应力传递机制
图13 为新建隧道沿A-A 截面推进的不同阶段既有隧道周围土体归一化纵向、横向、竖直应力比σxx/σv、σyy/σv、σzz/σv.其中,σxx为沿既有隧道轴线方向(x 方向)的正应力,σyy为沿新建隧道轴线方向(y方向)的正应力,σzz为竖直方向(z 方向)的正应力,σv为新建隧道未开挖时对应位置的竖向有效应力.S1和S2 分别选择拱顶、拱肩、拱脚和拱底作为监测点.
图13(a)为归一化应力比纵向方向上,当隧道掌子面达到y/D=-3 位置时,σxx/σv略有增加.当隧道掌子面接近既有隧道的中线时,S1 拱顶、拱肩应力比和S2 拱脚、拱底应力比均显著降低.当掌子面达到y/D=1.5 时,应力比达到最小值.当掌子面达到y/D=2时,S1 拱顶处应力比和S2 拱底处应力比略有增加.
在图13(b)中,当掌子面达到y/D=-3 时,隧道的横向应力发生了明显的变化.当y/D=-0.5 时,工况S1 拱肩和S2 的拱脚处横向应力比σyy/σv大大提高,当隧道开挖面到y/D=0.5 时,达到最大.S1 拱肩和S2 拱脚处应力比的增加和S1 拱顶和S2 拱底处应力比的减少表明,S1 拱顶和S2 拱底处的应力传递至S1 拱肩和S2 拱脚处.
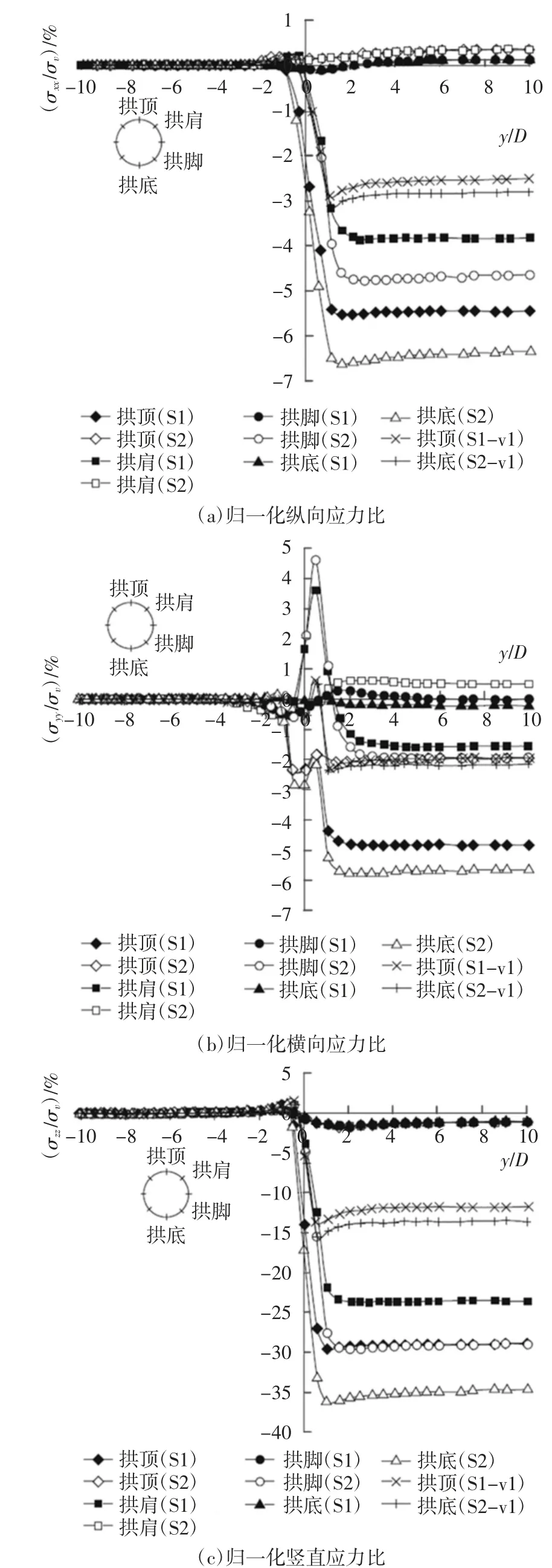
图13 沿既有隧道前进方向的归一化应力比Fig.13 Normalised stress ratios around the existing tunnels as tunnel face advances
3 结论
本文基于砂土亚塑性本构模型采用有限元分析方法进行了不同施工顺序的垂直交叉隧道数值试验,研究了施工顺序对垂直交叉隧道的影响及既有隧道附近土体的应力传递机制,得出以下结论:
1)与下穿工况相比,上穿工况的地表沉降较大,但影响范围较小.与无既有隧道工况相比,有既有隧道工况最大沉降量降低14%.下穿工况中新建隧道对既有隧道的影响在位移和变形上都比上穿工况更为显著.
2)上穿工况和下穿工况的最大弯矩分别出现在拱顶和拱底处,而最小弯矩出现在拱脚处.下穿工况中既有隧道的最大弯矩和最小弯矩的大小均大于上穿工况.
3)当新建隧道掌子面接近既有隧道中心线时,上穿工况的拱顶横向和纵向应力传递至拱肩,下穿工况的拱底横向和纵向应力传递至拱脚处.
4)有既有隧道工况下,当掌子面距离既有隧道中心线后方3D 和前方6D 之间时,应力释放对既有隧道的影响显著.
5)只考虑体积损失的工况的地表沉降小于同时考虑体积和质量损失的工况,而且既有隧道的竖向位移和变形、附加弯矩、轴向力均更小.
在垂直交叉隧道施工中,应充分考虑施工顺序对地表沉降、既有隧道的影响.本研究的局限性主要包括两个方面:首先,模拟中采用的土体本构模型不考虑土体的小应变(0.001%~1%)刚度.其次,干砂隧道衬砌的力学参数缺乏相应的工程背景.为了辅助工程设计,进一步的数值研究应结合具体的实际工程或模型试验.
