长期荷载作用下钢-混凝土组合梁的挠度计算与分析
2021-07-25冀伟孙斌白倩罗奎
冀伟,孙斌,白倩,罗奎
(1.兰州交通大学 土木工程学院,甘肃 兰州 730070;2.重庆市铁路集团有限公司,重庆 401120)
钢-混凝土组合结构可以充分发挥混凝土与钢材各自的优点,即混凝土主要抗压,钢材主要抗拉,结构受力较为合理.钢-混凝土组合结构特别适用于装配式中等跨径桥梁及快速施工的桥梁[1].在实际工程中,钢与混凝土的连接常采用剪力连接件,剪力连接件的变形会引起钢梁与混凝土板的界面滑移,降低组合梁整体刚度,从而产生附加变形.此外,钢-混凝土组合梁在长期荷载作用下,由于混凝土收缩徐变的影响,其挠度会随时间增加而增大,而梁变形过大会影响其正常使用性能[2].
Dezi 等[3-4]提出了考虑混凝土收缩徐变效应的钢-混凝土连续组合梁的时变分析方法.Cheng[5]以钢-混凝土组合T 梁为例,分析了滑移和混凝土收缩徐变对其应力和挠度的影响.Cao 等[6]对三根预应力钢-混凝土组合连续箱梁(无预应力、部分预应力和完全预应力)进行了420 d 的长期荷载试验,提出了考虑持续荷载、收缩、徐变及预应力组合效应对钢-混凝土组合连续箱梁长期挠度的计算模型.Tong 等[7]建立了考虑混凝土徐变、收缩和开裂的三维黏弹塑性损伤本构模型,研究了预应力钢-混凝土组合梁的短期和长期性能.项贻强等[8]在考虑体外预应力和混凝土长期性能对钢-混组合梁界面滑移影响的基础上,提出界面滑移时变的计算公式,并探讨了钢-混组合梁在混凝土长期效应作用下的滑移变化规律.肖岩等[9]在考虑界面滑移效应的基础上,提出了钢-混组合梁挠度计算的二阶算法,并求得4 种不同边界条件下组合梁的挠度.冀伟等[10]在考虑钢梁与混凝土板的滑移效应和组合梁剪切变形的基础上,运用能量变分原理求得了钢-混凝土组合梁的挠度计算公式.褚少辉等[11]运用有限元分析研究了钢-混组合梁的滑移分布规律与特点.Nguyen 等[12]提出可以考虑混凝土收缩、徐变和开裂之间相互作用的非线性时变特性钢-混组合梁有限元模型.
综上,国内外学者已对钢-混凝土组合梁的界面滑移效应和长期荷载效应进行了研究,但对同时考虑钢-混组合梁全截面剪切变形、钢-混接触面的滑移效应及混凝土长期效应下钢-混凝土组合梁的挠度计算还存在不足.因此,本文在综合考虑上述三种效应的基础上,运用能量变分原理建立了钢-混组合梁挠度计算的控制微分方程,引入梁弯曲角、剪应变和挠度的微分关系,按照给定的自然边界条件求得钢-混组合梁在长期荷载作用下挠度的计算公式.同时,钢-混凝土组合梁的高跨比对梁的剪切变形有影响,因组合梁属于薄壁构件,往往承担较大的荷载,其跨高比较小,将导致剪切影响系数较大,使剪切变形成为一个不可忽略的因素[13];文献[10]研究了混凝土与钢梁的界面连接对层间滑移的影响,在其他条件不变的情况下,抗剪刚度越小,层间滑移效应对挠度的影响越不可忽略,因此有必要在计算中对层间滑移与剪切变形两种效应予以综合考虑.本文基于以上条件,通过简支和两跨连续钢-混组合梁的实例验证了所得计算公式的正确性和适用性,研究成果可为实际工程中钢-混凝土组合梁在长期荷载效应下的挠度计算提供理论依据.
1 钢-混凝土组合梁挠度计算的控制微分方程
1.1 基本假定
运用能量变分原理对钢-混凝土组合梁的挠度进行分析时,引入以下基本假定[14-15]:
1)混凝土桥面板与钢梁的横截面均符合平截面假定,剪力连接件为等效的均匀连续弹性介质;
2)钢梁与混凝土在整个受力阶段的应力-应变关系为线性关系,混凝土在整个受力阶段未开裂、剥落;
3)忽略钢-混组合梁的掀起现象,不考虑其横向变形,混凝土桥面板与钢梁的曲率完全相等;
4)忽略桥面板剪力滞效应对钢-混组合梁挠度的影响.
1.2 考虑层间滑移效应影响
假定层间滑移界面符合Goodman 弹性夹层假设(如图1 所示),ks为剪力连接件的抗剪刚度,实际工程中应根据混凝土标号、栓钉长短、间距、直径和抗剪切联接度等参数的影响对剪力连接件进行抗剪实验来确定实际抗剪刚度;Es、As与Ec、Ac分别为钢与混凝土材料的弹性模量和截面积.如图2 所示的钢-混组合梁,hc、hs分别为混凝土板和钢梁各自截面中性轴到组合截面中性轴的距离,h 为hc和hs之和;Hc、Hs分别为混凝土桥面板和钢梁截面的形心,H 为钢-混组合梁截面的形心.在外力作用下的钢-混组合梁,组合截面的弯曲变形和剪力连接件的剪切变形将产生层间相对滑移.图2 中,εcs、εss分别为滑移效应引起的混凝土桥面板和钢板的应变,θ 为组合梁的弯曲角.
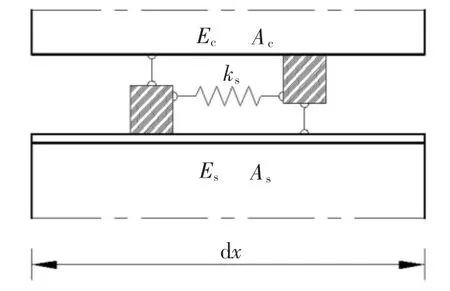
图1 弹性夹层假设Fig.1 Assumption of elastic sandwich

图2 考虑滑移效应影响下钢-混凝土组合梁截面应力分布Fig.2 Strain distribution of steel-concrete composite girder considering the interlayer slipping
考虑层间界面钢-混组合梁的轴力自平衡条件,可得:

式中:u′(x)为混凝土桥面板与钢梁相对滑移应变.
由公式(1)和(2)可得层间滑移引起的混凝土与钢梁的滑移应变:
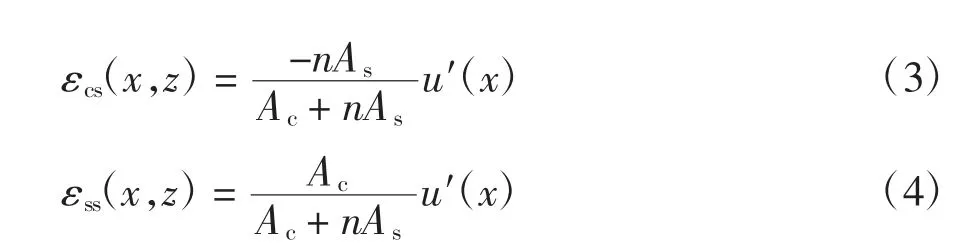
式中:n=Es/Ec为钢材与混凝土弹性模量之比.
1.3 考虑组合梁全截面剪切变形影响
钢-混组合梁由截面竖向剪力引起的剪切变形会使得梁发生翘曲(如图3 所示),从而引起梁的附加挠度.
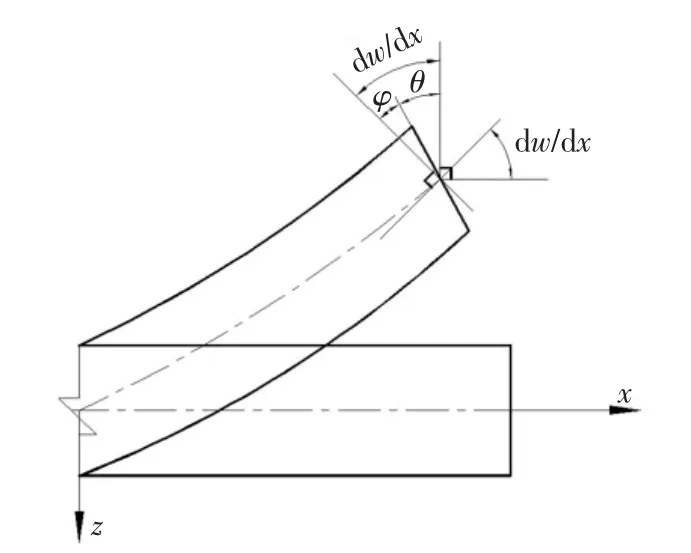
图3 考虑剪切变形的梁转角示意图Fig.3 Angle of the girder considering shear deformation
根据钢-混组合梁的剪切变形理论,其全截面弯曲角θ、平均剪应变φ 及挠度w 之间的关系为:

组合梁的平均剪应变可表示为:

钢-混组合梁剪切变形应变能为:

式中:ξ、A、SZ、bZ和I 分别为组合梁按照混凝土材料换算后的截面剪应力分布不均匀系数、截面总面积、截面面积矩、截面宽度和截面惯性矩.
1.4 混凝土长期效应下控制微分方程的建立
考虑钢-混组合梁全截面的剪切变形、层间滑移效应的基础上,引入混凝土收缩应变εcss(t,ts),则混凝土板和钢梁的弯曲总应变为:
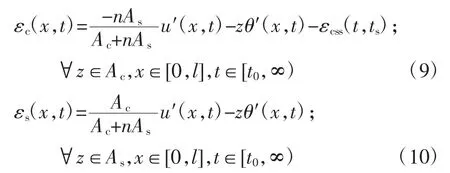
式中:t、t0和ts分别为计算时刻混凝土龄期、混凝土加载龄期和收缩开始时刻混凝土龄期;l 为梁长.
采用按龄期调整的有效模量法,并引入老化系数ρ(t,t0),推导可得随徐变系数发展的有效弹性模量EΦ:

式中:φ(t,t0)为混凝土的徐变系数.
建立钢-混凝土组合梁的应变能方程:
桥面板应变能表示为

钢梁应变能表示为

弹性夹层滑移应变能为

组合梁剪切应变能表示为

考虑M(x)为外荷载作用下的弯矩,则外荷载的势能为:

在外力作用下的结构处于平衡状态,由最小势能原理可知总势能的一阶变分为零:

将表达式(12)~(16)代入式(17),运用变分法计算可得如下微分方程组和边界条件:
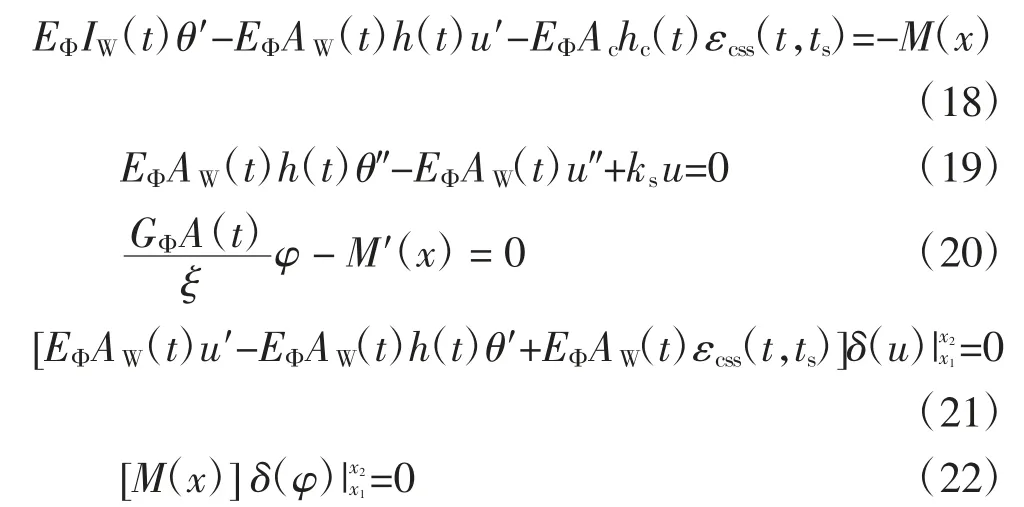
式中:IW(t)=Ic+(t)+n(t)Is+n(t)As(t),IW(t)为t 时刻钢-混组合梁以混凝土材料换算的截面惯性矩,Ic、Is分别为混凝土板和钢梁的惯性矩;AW(t)=n(t)AsAc/(n(t)As+Ac),n(t)=Es/EΦ,为t 时刻钢材与混凝土弹性模量之比;A(t)=n(t)As+Ac,为t 时刻组合梁以混凝土材料换算的截面面积.

式中:u*是与梁段剪力有关的微分方程的特解;Λ1、Λ2为实常数.
方程式(18)为组合梁考虑混凝土收缩徐变效应下挠度转角和滑移的基本微分方程,整理得:
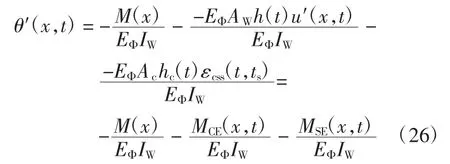
式中:MCE(x,t)=-EΦAWh(t)u′(x,t)为考虑徐变和滑移效应产生的附加弯矩;MSE(x,t)=-EΦAchc(x,t)εcss(t,ts)为考虑收缩效应的附加弯矩.
由(26)式可以看出,考虑滑移和收缩徐变效应后,组合梁弯矩进行了重新分配,增加了附加弯矩修正项MCE(x,t)和MSE(x,t),且随着组合梁曲率增大,大大降低了结构刚度.
整理式(20)~(26),并积分可得组合梁挠度:
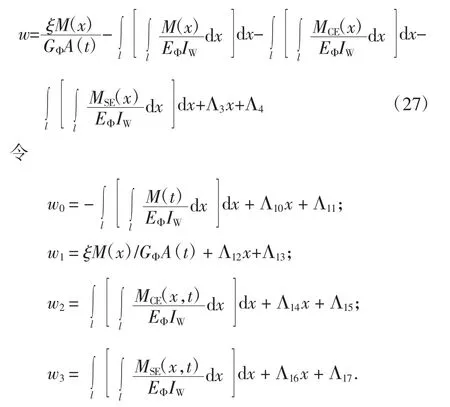
重新整理式(27),可得:

式中:w0为组合梁初等梁理论计算得到的挠度;w1为组合梁剪切变形所产生的附加挠度;w2为组合梁层间滑移变形所产生的附加挠度;w3为组合梁层间收缩效应所产生的附加挠度;Λ3、Λ4、Λ10、Λ11、Λ12、Λ13、Λ14、Λ15、Λ16、Λ17均为常实数,依据自然边界条件确定.
2 静定组合梁滑移和挠度计算理论解
静定梁以跨径为l 的简支组合梁承受均布荷载q 作用为例,如图4 所示,其弯矩与剪力的函数如式(29)所示.

图4 受均布荷载作用的简支梁Fig.4 Simply-supported girder subjected to uniformly distributed loads

2.1 考虑徐变效应影响下组合梁的滑移位移
引入随徐变系数发展的有效弹性模量EΦ,即可考虑组合梁徐变效应对层间滑移的影响,将式(29)代入式(23)得:
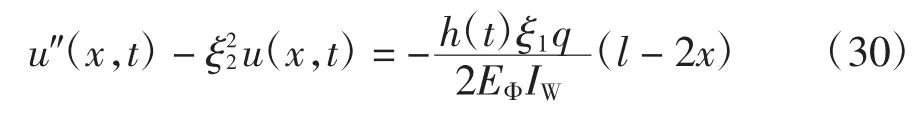
求解得方程通解:

由边界条件:x=0 时,u′=0;x=l 时,u=0,整理可得u 的解为:

2.2 挠度计算理论解
1)初等梁理论挠度w0
由边界条件:x=0 时,w0=0;x=l 时,w0=0,整理可得w0的解为:

2)剪切变形所产生的挠度w1

3)层间滑移所产生的挠度w2
滑移位移u 一阶偏导数为:

4)考虑收缩效应w3
对简支组合梁,其层间收缩效应所产生的附加挠度由混凝土层收缩变形产生的弯矩[16]引起,如图5和图6 所示.

图5 收缩变形引起的截面力Fig.5 Sectional forces caused by shrinkage deformation

图6 收缩效应下的附加弯矩Fig.6 Additional bending moment caused by shrinkage
由边界条件:x=0 时,w3=0;x=l 时,w3=0,整理得w3的解为:
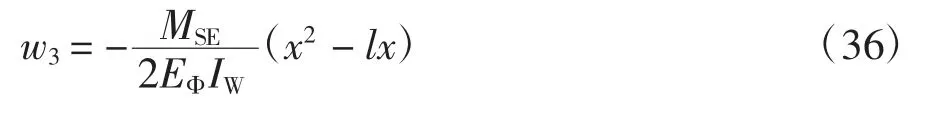
3 超静定组合梁滑移和挠度理论解
超静定梁以均布荷载q 作用下的两跨连续梁为例,如图7 所示.根据力学知识计算得A、B、C 三处支座反力为RA=0.375ql,RB=1.25ql,RC=0.375ql.考虑滑移解超静定后,支反力不为初等梁体支反力,需结合荷载作用下简支梁跨中挠度求解超静定支反力.
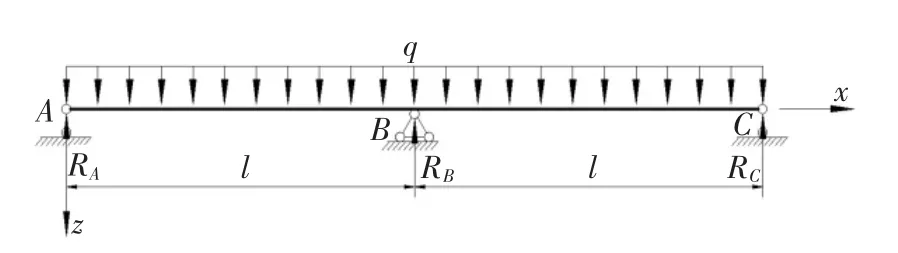
图7 两跨连续组合梁受均布荷载Fig.7 Continuous composite beam under uniform load
对称荷载作用下,取单跨(左跨0 ≤x ≤l)为研究对象,则组合梁弯矩和剪力函数表示如下:
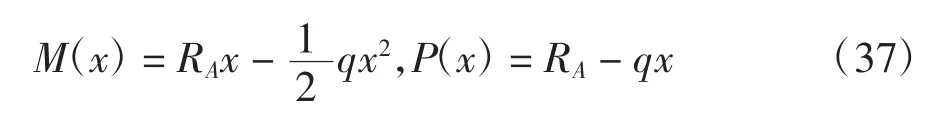
3.1 考虑徐变效应下连续梁的滑移位移
将式(34)代入式(23)得方程通解:
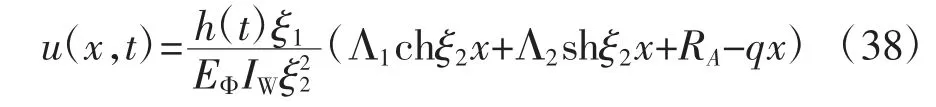
由边界条件:x=0 时,u′=0;x=l 时,u=0,整理可得u 的解为:
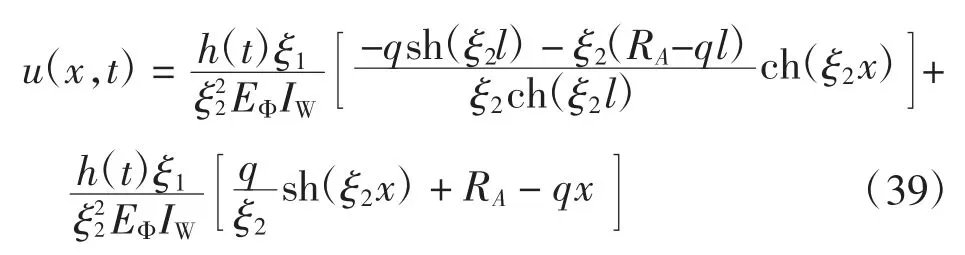
3.2 连续梁的挠度计算
1)初等梁理论挠度w0
引入边界条件并整理得w0的解为:

2)剪切变形产生挠度w1
3)层间滑移所产生的挠度w2
滑移位移u 的一阶偏导数:

引入边界条件并整理得w2的解为:
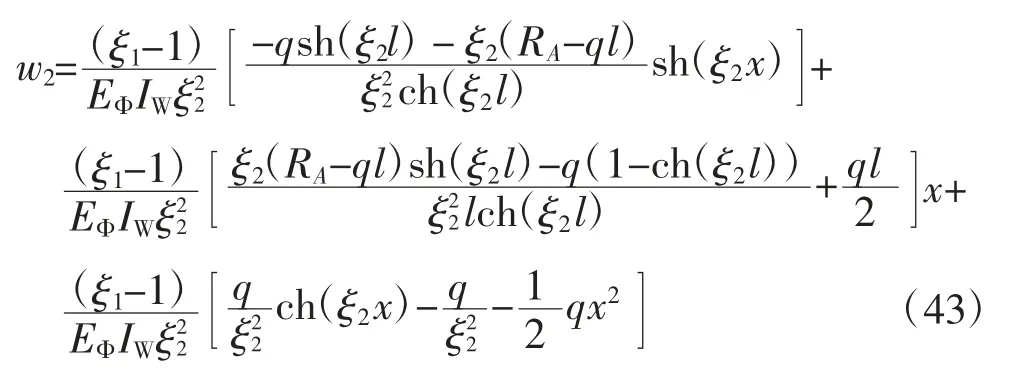
4)考虑混凝土收缩效应w3
如图8 所示的两跨连续梁,解除中支座处的约束,由此产生的次弯矩X1用来考虑约束对收缩效应的影响.图8 中,收缩应变产生的附加弯矩为MSE,X1在中支点处产生的转角等同于收缩效应在中支点处产生的转角.建立力学基本体系,由图乘法可求得收缩效应产生的中支点次弯矩X1.

图8 次弯矩X1 作用Fig.8 Secondary moment action
收缩效应与次弯矩共同作用的变形条件为:

式中:δ11、Δ1SE分别为单位弯矩和收缩效应在X1方向上产生的转角.
收缩效应所产生的附加挠度w3为:

由边界条件:x=0 时,w3=0;x=l 时,w3=0,整理得w3的解为:
4 算例分析
4.1 简支组合梁算例
选取文献[17] 中的钢-混凝土组合实验梁试件LCB1 及LCB2 为研究对象,用于验证本文所得挠度计算公式的正确性.LCB1 和LCB2 试件中钢梁与混凝土翼板梁跨均为4 m,图9 为LCB1 和LCB2 的截面示意图.钢梁材质为Q235b,弹性模量为2.1×105MPa.试件LCB1 翼板混凝土材料为C20,轴心抗压标准值fck=20 MPa,龄期28 d 弹性模量为3.18×104MPa,试件LCB2 翼板混凝土材料为C30,轴心抗压标准值fck=30 MPa,龄期28 d 弹性模量为3.47×104MPa.文献[17]的简支试验梁是按完全抗剪连接设计的,即抗剪刚度趋于无穷,而滑移效应趋于0,本例假定抗剪刚度过大而忽略滑移位移.两试件均承受满跨均布荷载6.23 kN/m.
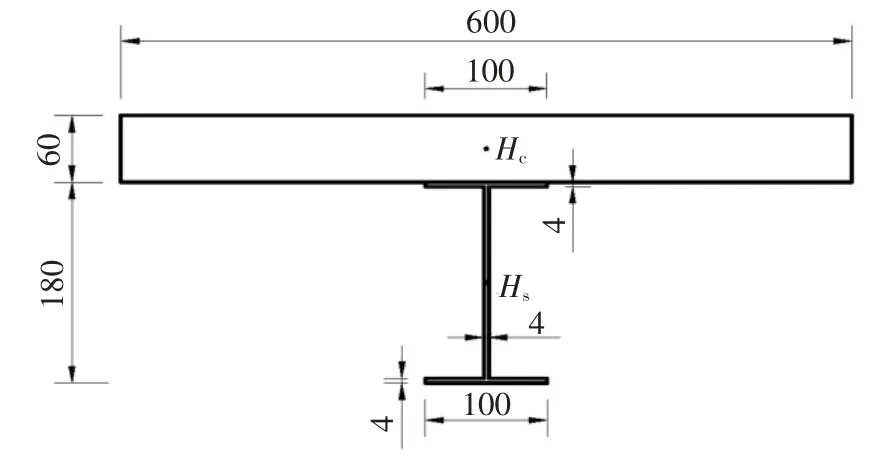
图9 组合梁截面尺寸(单位:mm)Fig.9 Section dimensions of composite girder(unit:mm)
根据CEB-FIP(MC90)规范,采用Midas Civil 有限元软件模拟在平均湿度为67%、构件理论厚度为54.5 mm 下,C20 与C30 混凝土的徐变系数与收缩应变在加载1 000 d 内的发展情况,如图10 所示.有限元考虑收缩徐变框图和算法如图11 所示.

图10 徐变系数与收缩应变随时间的发展Fig.10 Development of creep coefficient and shrinkage strain versus time curves

图11 有限元考虑收缩徐变计算框图Fig.11 Flow chart of finite element considering shrinkage and creep
采用有限元Midas Civil 软件建立了试件LCB1、LCB2 的有限元模型,由于在Midas 有限元模型中采用双单元法刚性连接建模时,混凝土板部分在徐变作用下产生一定误差,因此,本文整体采用标准截面法(组合梁截面)建模.
本文根据静定结构的收缩和徐变引起结构的变形、超静定结构的收缩和徐变引起结构次内力进而引起结构变形的原理进行了收缩徐变的数值运算.在有限元计算中,收缩徐变只有与施工过程结合才有意义,桥梁结构分析中应分阶段,按施工顺序考虑收缩徐变效应,本文最终挠度计算结果为有限元模型挠度计算值叠加层间滑移挠度理论计算值.
Midas Civil 实现混凝土的收缩和徐变一般分两个步骤:一是定义收缩、徐变系数;二是将定义的收缩徐变模式赋予材料.图12 对应为简支梁试件LCB1、LCB2 的计算模型,两试件区别在于混凝土的轴心抗压标准值和龄期28 d 弹性模量值不同.通过建立试件LCB1 的有限元模型并求解出对应的挠度值,然后改变模型组合梁截面中混凝土材料及相应的弹性模量,重新将定义的收缩徐变模式赋予混凝土材料,运算求解试件LCB2 对应挠度值.模型中纵向划分为20 个单元和21 个节点,单元长度等分为0.2 m,约束布置以梁左端为固定铰支座,右端为活动铰支座,通过改变模型混凝土材料特性分析试件LCB1、LCB2 挠度变化情况.

图12 组合梁的Midas 模型Fig.12 Midas model of composite girder
将理论公式计算的跨中挠度值与有限元值及实测值进行对比分析,对比结果见表1.

表1 试件LCB1、LCB2 跨中挠度对比Tab.1 Comparison of mid-span deflection
从表1 中可以看出,理论公式计算的挠度值与有限元值及实测值的误差在5%以内,吻合较好,验证了所推导的钢-混组合梁计算公式的正确性.试件LCB1、LCB2 加载500 d 后的理论挠度计算结果,如图13 所示.

图13 混凝土收缩徐变效应对挠度影响Fig.13 Effects of creep and shrinkage on the deflection
由图13 中可见,简支钢-混组合梁加载500 d后,试件LCB1 收缩徐变后的挠度是瞬时挠度的2.55 倍,试件LCB2 收缩徐变后的挠度是瞬时挠度的2.49 倍,可见混凝土的收缩徐变效应对挠度的影响较大.
4.2 两跨连续组合梁算例
选取文献[3]中的两跨连续钢-混凝土组合梁试件进行长期荷载效应分析,梁跨为2×25 m,承受满跨均布荷载64.56 kN/m,其横截面尺寸如图14 所示,抗剪刚度取值参考文献[18],取ks=400 MPa.
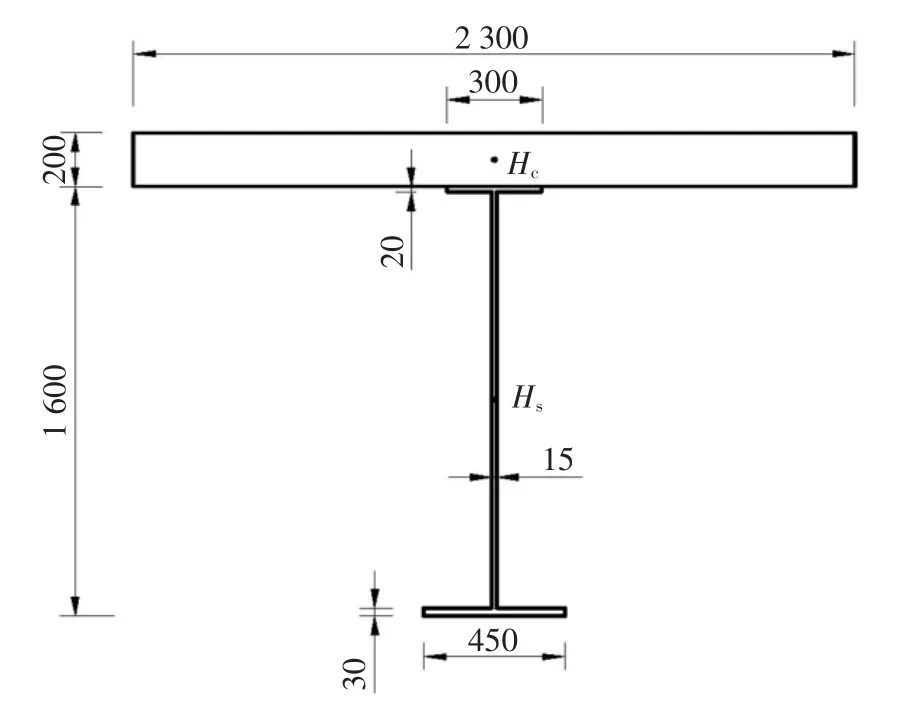
图14 两跨连续梁截面尺寸(单位:mm)Fig.14 Section dimension of continuous girder(unit:mm)
采用Midas Civil 2018 有限元软件建立了两跨连续钢-混组合梁桥的三维有限元模型,模型中纵向划分为26 个单元和27 个节点,其中单元长度为2 m,跨中处分割单元为1 m,约束布置以梁两端为活动铰支座,跨中为固定铰支座,如图15 所示.

图15 两跨连续钢-混组合梁的MIDAS 模型Fig.15 MIDAS model of two span continuous composite beam
从表2 中可知,本文理论公式计算的挠度值与有限元值吻合较好,验证了所推导的两跨连续钢-混组合梁挠度计算公式的正确性.为进一步验证本文理论公式的正确性,在考虑混凝土收缩徐变效应下将本文公式计算求得的中支点反力与文献[3]的中支点反力进行对比分析,二者吻合较好,如图16 所示.

表2 连续组合梁最大挠度对比Tab.2 Comparison of maximum deflections of continuous composite girder
首先对比分析了两跨连续钢-混凝土组合梁在以下三种情况下的挠度:①初等梁理论(C)计算所得挠度;②初等梁理论(C)+考虑全截面剪切变形(Q)计算所得挠度;③初等梁理论(C)+考虑全截面剪切变形(Q)+考虑层间滑移(R)计算所得挠度,对比结果如图17 所示.

图17 不同情况下挠度分析对比Fig.17 Comparison of deflection analysis in different situations
从图17 中可以看出,在初等梁理论基础上考虑层间滑移效应和剪切变形效应后,跨间最大挠度增长了37.4%,仅剪切变形效应引起的挠度增加了14.2%.可见,剪切变形效应和层间滑移效应对钢-混凝土连续梁挠度的影响不可忽略.
在图17 情况③的基础上考虑混凝土收缩徐变效应对两跨连续钢-混组合梁挠度影响.从加载时刻算起,在混凝土收缩徐变时效期为70 年,考虑周边环境相对湿度为50%,结构构件理论厚度为h=184 mm,轴心抗压标准值30 MPa.混凝土板徐变系数与收缩应变发展按照CEP-FIP(MC90)的规定进行计算求得,如图18 所示.采用本文所得的理论计算公式求得了两跨钢-混连续组合梁在加载70 年后跨中挠度的发展情况,如图19 所示.
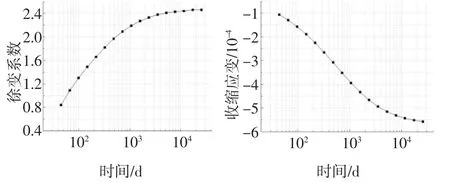
图18 徐变系数与收缩应变随时间的发展Fig.18 Development of creep coefficient and shrinkage strain versus time curves
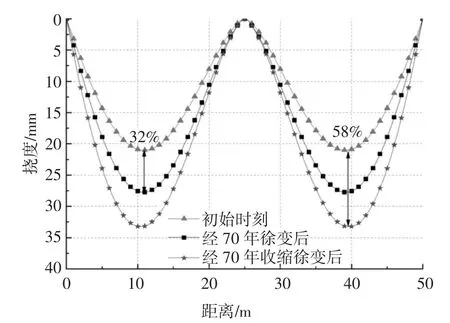
图19 挠度的收缩徐变效应分析Fig.19 Deflection analysis under shrinkage and creep
从图19 中可以看出,在初始时刻考虑剪切变形效应和层间滑移效应,组合梁经70 年加载后,仅考虑混凝土徐变效应下产生的挠度是瞬时加载挠度的1.32 倍,考虑混凝土收缩徐变效应产生的挠度是瞬时挠度的1.58 倍.因此,混凝土长期荷载效应对两跨连续钢-混组合梁的挠度有较大影响,不可忽略.
5 结论
本文对考虑钢-混组合梁剪切变形、层间滑移效应和混凝土桥面板收缩徐变效应下的钢-混凝土组合梁挠度进行计算与研究分析,所得结论如下:
1)本文推导所得长期荷载作用下钢-混凝土组合梁挠度计算公式的正确性得到有限元和实测值的验证,理论公式推导过程简单,物理意义明确,且能满足工程计算精度要求.
2)考虑混凝土收缩徐变后,简支钢-混组合梁跨中最大挠度比加载瞬时挠度增大1.55 倍,可见混凝土的收缩徐变效应对简支钢-混组合梁挠度的影响较大.
3)考虑层间滑移效应和剪切变形效应,两跨连续钢-混组合梁最大挠度在初等梁理论基础上增长了37.4%,仅考虑剪切变形效应引起的挠度增加了14.2%.可见,剪切变形效应和层间滑移效应对钢-混连续梁挠度的影响不可忽略.
4)考虑剪切变形效应和层间滑移效应,两跨连续钢-混组合梁经70 年加载后,仅考虑混凝土徐变效应下产生的挠度是瞬时加载挠度的1.32 倍,考虑混凝土收缩徐变效应产生的挠度是瞬时挠度的1.58倍.因此,混凝土长期荷载效应对两跨连续钢-混组合梁的挠度有较大影响,在工程设计和施工中应引起重视.
