钢纤维混凝土的本构模型及力学性能分析
2021-07-25毕继红霍琳颖赵云王照耀
毕继红,霍琳颖,赵云,王照耀
(1.天津大学 建筑工程学院,天津 300350;2.滨海土木工程结构与安全教育部重点实验室,天津 300072)
纤维混凝土在工程建设中越来越多的被使用,而钢纤维是实际工程应用中最常用的纤维类型[1-3].加入钢纤维可以在保持混凝土原有优势的基础上,对普通混凝土易开裂,抗拉、抗弯强度低以及韧性差等不足有了显著改善,使混凝土在工程中有更广泛的应用前景[4-5].
国内外学者关于钢纤维混凝土(SFRC)的力学性能做了大量的相关试验,梁兴文等人[1-2]做了大量的纤维混凝土的抗拉试验和纤维混凝土梁的四点弯曲试验,并拟合了钢纤维混凝土的单向受拉本构模型和梁的抗弯强度的计算公式;邓宗才[4]进行161 个三点弯曲梁的断裂试验,测定了不同纤维掺量下试件的荷载-挠度曲线.通过大量的力学试验可知,在混凝土开裂后,钢纤维在开裂面上纤维桥接现象,对混凝土的抗拉强度、抗折强度、韧性均有显著提高作用.
钢纤维混凝土力学性能的研究远不能满足实际工程的需要,目前主要依靠试验和对试验结果的拟合,缺乏理论支撑.近年来,钢纤维混凝土力学性能的理论研究引发了国内外学者的广泛关注.通常基于经典的混凝土本构模型,包括:混凝土弥散本构模型、混凝土损伤本构模型以及混凝土断裂模型,考虑钢纤维对混凝土基体的增强作用,从而建立钢纤维混凝土的本构模型.池寅等人基于有限元软件ABAQUS 中混凝土的损伤本构模型,考虑纤维对混凝土受拉屈服函数和损伤因子的确定的影响,建立了考虑纤维作用的混凝土损伤本构模型;Olesen[7]基于混凝土断裂力学中虚拟裂纹模型,在裂缝扩展中将纤维视为铰链,分层考虑纤维和混凝土对承载力的贡献;薛云亮等人[8]通过大量的纤维混凝土试验,基于两参数Weibull 分布函数引入纤维对损伤本构中损伤阈值影响,建立了可考虑损伤阈值影响的钢纤维混凝土损伤本构模型.
然而,现有的纤维混凝土本构模型,通常认为在混凝土开裂后,纤维在裂缝扩展过程中增强作用保持不变.事实上,随着混凝土裂缝的扩展,开裂面上的钢纤维与混凝土基体间拔出过程分为部分脱黏和完全脱黏两个阶段,这2 个阶段具有不同的纤维增强应力.
在混凝土开裂后,充分考虑钢纤维在混凝土中由充分黏结、逐渐脱黏直到完全脱黏,然后拔出的全过程,本文提出了一个三维钢纤维随机分布的混凝土弥散开裂本构模型.并利用Fortran 编程,通过有限元软件ABAQUS 的子程序接口Umat,将本文提出的钢纤维混凝土本构模型引入ABAQUS 的材料库中,并利用该本构模型在ABAQUS 中建立混凝土受拉试件和四点弯曲梁的有限元模型.通过比较试验数据和数值模拟结果,验证了所提出的材料本构模型的准确性.
1 混凝土及纤维的本构模型
在钢纤维混凝土中,钢纤维作为掺加物加入混凝土基质中,其中对混凝土基质采用弥散开裂本构模型,对掺入的钢纤维采用理想弹塑性本构模型.
1.1 弥散开裂本构模型
基于应力空间下的屈服函数和与屈服函数相关的流动准则,充分考虑混凝土的受压硬化/受拉软化现象,建立混凝土的弥散开裂本构模型[9].在弹性受力阶段,混凝土服从广义的虎克定律,如公式(1).

混凝土进入塑性阶段后,采用弹塑性本构模型[10],可表示如下:
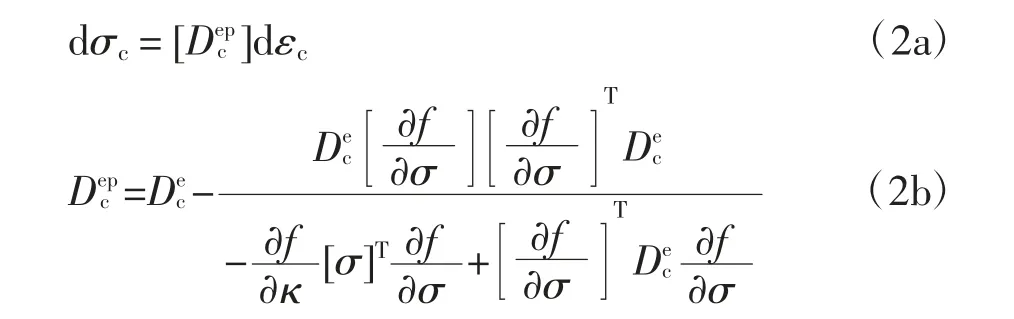
式中:dσc和dεc分别是混凝土应力增量和应变增量;[] 是普通混凝土的弹塑性刚度矩阵;κ 是混凝土屈服函数的硬化软化参数;f 是混凝土的屈服函数.本文采用有限元软件ABAQUS 中混凝土弥散开裂本构模型所提供的屈服函数[11-13].
1.2 理想弹塑性本构模型
在钢纤维混凝土中通常选用冷拔钢纤维,其抗拉强度通常在1 000~2 000 MPa,弹性模量在200 GPa 以上,钢纤维的弹性模量和抗拉强度都远高于普通混凝土[14].因此假设钢纤维在混凝土中始终处于弹性状态,且作为添加物,仅考虑钢纤维在轴线方向的受拉情况,忽略钢纤维的弯曲变形和径向收缩[15].本文针对圆形截面且具有高长径比的钢纤维,采用钢材的理想弹塑性本构模型计算混凝土中加入钢纤维的应力-应变关系.纤维在未达到抗拉强度时,纤维应力与应变呈线弹性;在达到抗拉强度后,纤维应力不再随应变提高.

式中:σf和εf分别是钢纤维轴向应力和应变;Ef是钢纤维弹性模量;σfu是钢纤维抗拉强度.
2 受压状态下的钢纤维混凝土
2.1 钢纤维混凝土弹性阶段的本构模型
在混凝土的弹性阶段,混凝土通过与钢纤维之间的界面黏结力,将荷载传至钢纤维,二者变形协调,使钢纤维与混凝土基体作为一个整体共同承担荷载.此时,钢纤维作为混凝土基质中的简单添加物,由于钢纤维具有优异的力学性能,通过两相复合理论,使钢纤维混凝土的弹性模量有明显提高.基于掺入钢纤维的体积分数,计算钢纤维混凝土的弹性模量[16],如公式(4)所示.
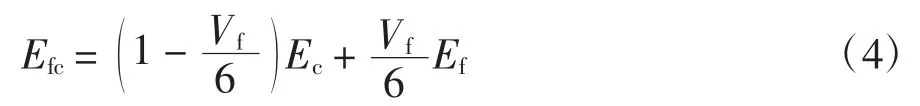
式中:Efc和Ec分别是钢纤维混凝土和混凝土的弹性模量;Vf是钢纤维在混凝土中的体积分数.
忽略钢纤维对混凝土泊松比的影响,假设钢纤维混凝土的泊松比与普通混凝土一致[5].并将钢纤维混凝土的弹性模量代入普通混凝土的弹性刚度矩阵中,可得钢纤维混凝土的弹性刚度矩阵.在弹性阶段的钢纤维混凝土的本构模型如下:

2.2 钢纤维混凝土受压状态下的本构模型
混凝土在受压屈服后的强化、软化阶段均没有开口裂缝的产生,因此钢纤维在开裂面上无法形成桥接作用.纤维仅由自身优异的力学性能提高混凝土弹性刚度矩阵,从而提高混凝土的抗压能力.将钢纤维混凝土的弹性刚度矩阵代入到公式(2)中,钢纤维混凝土在受压情况下的本构模型,如公式(6).
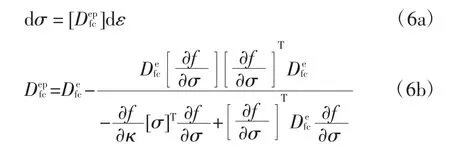
式中:dσ 和dε 分别是纤维混凝土的应力增量和应变增量,是纤维混凝土的弹塑性刚度矩阵.
3 纤维在裂缝处的增强作用
在混凝土开裂前,钢纤维没有桥接作用,因此钢纤维不影响混凝土的开裂应力[17-18].在混凝土开裂后,钢纤维在混凝土开裂面上,形成纤维桥接,主要承担开裂后的荷载.钢纤维可以有效阻止混凝土裂缝的扩展[17].
3.1 混凝土的开裂准则及裂缝宽度
由于钢纤维不影响混凝土的开裂强度,因此钢纤维混凝土的开裂准则,仍采用普通混凝土的判别方式.本文所采用的是ABAQUS 中混凝土弥散开裂本构模型的开裂准则,将混凝土的受拉屈服面作为“裂缝检测面”,当混凝土应力达到裂缝检测面时,裂缝出现[17].混凝土的裂缝方向被定义为最大主塑性应变增量与混凝土受拉屈服面所共轭的方向.
基于在ABAQUS 中混凝土弥散开裂本构模型对裂缝宽度的定义[17],裂缝宽度等于单元塑性应变乘以单元长度,如公式(7)所示.

式中:u 是在有限元模型中单元的裂缝宽度;εp是混凝土的塑性应变值;Lc是单元的长度.
3.2 混凝土中钢纤维取向的简化
钢纤维作为掺加物在混凝土基质中随机均匀分布,如图1 所示,图中θ 指纤维与混凝土开裂面法向形成的夹角.通过对钢纤维与混凝土开裂面法线夹角θ 进行积分得到随机均匀分布在混凝土基质中钢纤维的角度取向系数[19-21].
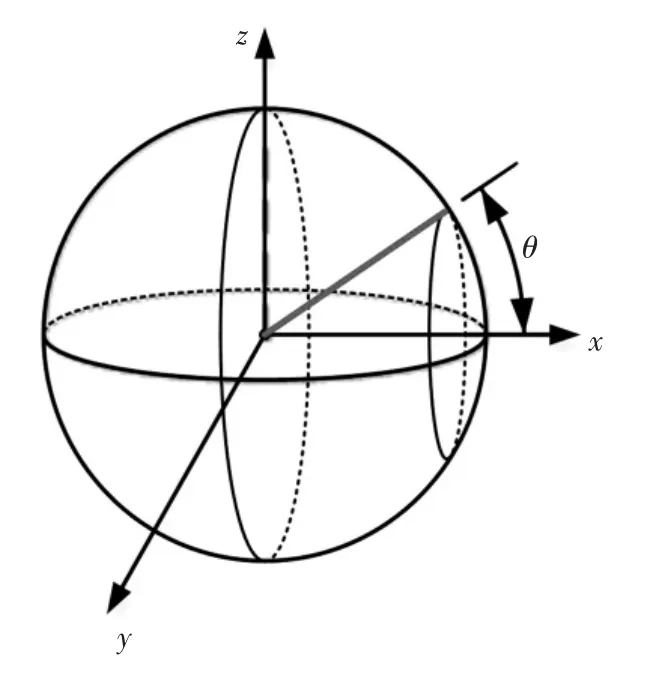
图1 钢纤维取向的示意图Fig.1 The orientation of the steel fiber
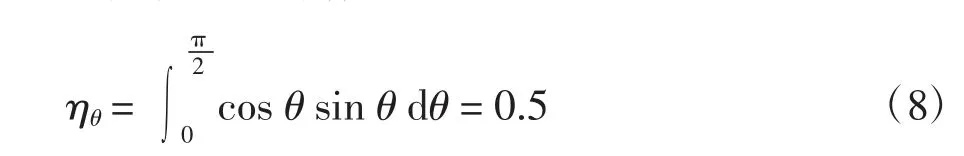
式中:ηθ是纤维在混凝土中的角度取向系数.
利用纤维的角度取向系数ηθ,将随机乱向分布的纤维简化为在垂直于开裂面方向的钢纤维,得到钢纤维的有效长度,即钢纤维在混凝土开裂面法线方向的投影长度.

式中:lf和Lf分别是钢纤维在混凝土中三维随机分布的有效长度和真实长度.
由于混凝土开裂面上埋深长度较短一侧的纤维黏合强度更弱,将优先被拔出,因此较短侧纤维埋深长度被考虑为纤维埋深长度le,较长一侧被认为始终与混凝土完全黏结[22].钢纤维在混凝土中均匀分布,钢纤维埋深长度的取值范围从最小值0 到最大值纤维有效长度的一半.对单根纤维的埋深长度进行积分计算可以得到纤维埋深长度le.

式中:le是纤维的埋深长度.
3.3 纤维混凝土界面的黏结滑移模型
钢纤维具有圆形横截面和较高的抗拉强度,纤维长径比在40~100 之间,随着混凝土裂缝开展,钢纤维逐步从混凝土基质脱黏、拔出,且不会被拉断[23].因此,将钢纤维混凝土中开裂面上的单根钢纤维取为隔离体,如图2 所示.并采用剪滞模型[22],计算钢纤维一个微段中力的平衡公式,如公式(11)所示.
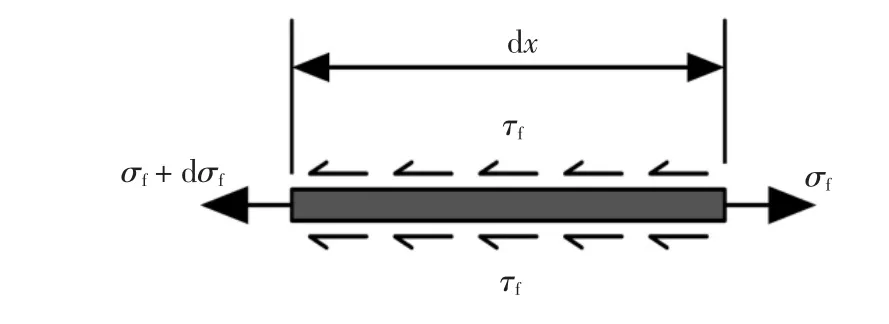
图2 纤维隔离体上的应力分布Fig.2 The stresses of the free-body in the fiber

式中:τf是开裂面上钢纤维与混凝土之间的平均剪应力;df是钢纤维的直径.
在纤维混凝土开裂后,纤维在混凝土开裂面上的桥接作用包括以下两个阶段:在纤维部分脱黏时,利用黏结滑移模型[24]模拟钢纤维与混凝土之间的界面脱黏过程;在纤维完全脱黏后,采用摩擦理论[25-26]模拟钢纤维在混凝土空腔内的拔出行为.
考虑纤维在混凝土开裂面上部分脱黏情况,给出了钢纤维混凝土界面剪应力计算公式如下[22]:

式中:τave是钢纤维与混凝土界面平均黏结强度;sf是钢纤维的伸长量;sfmax是纤维部分脱黏状态下纤维最大伸长量.
当混凝土开裂面上的钢纤维完全脱黏后,钢纤维在混凝土空腔的滑动,钢纤维与混凝土界面之间的剪应力由摩擦力提供.

式中:Pmax指单根钢纤维的拔出力;Af是纤维的横截面积.

当混凝土裂缝宽度超过sfmax时,钢纤维与混凝土完全脱黏.此时,纤维对混凝土增强作用仅由摩擦力提供[25].

式中:μ 是钢纤维与混凝土之间的摩擦系数[27];σN是混凝土对钢纤维的环向压应力.
3.4 钢纤维混凝土的本构模型
钢纤维通过与混凝土界面上的黏结滑移模型,对开裂后混凝土起到显著的增强效果.因此,在混凝土弥散开裂本构模型的基础上,增加一个附加项来表示钢纤维对混凝土的增强作用:
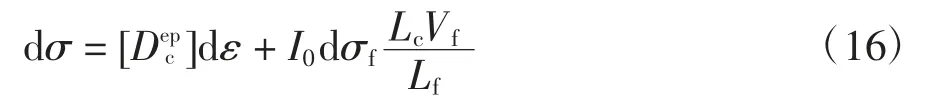
式中:I0是钢纤维在整体坐标系中的方向矩阵.
为保证在模拟计算中随机分布的纤维都会通过开裂面,且仅通过一个开裂面.因此,本文假设单元长度等于钢纤维的有效长度,即Lc=lf,建立了钢纤维混凝土的弥散开裂本构模型.
本文系统考虑了纤维在混凝土受拉开裂后的增强作用,分别建立了纤维部分开裂状态和开裂完全状态下的基于弥散开裂的本构模型,并将纤维掺量、长度、直径等钢纤维特性直接引入本构模型中,如下所示.
纤维部分脱黏时:

4 有限元模型的试验验证
基于Fortran 编程和有限元软件ABAQUS 中的自定义材料本构模型的子程序接口Umat,将钢纤维混凝土的本构模型引入到ABAQUS,并用于有限元数值模拟[28].图3 给出了子程序Umat 编程计算中的一个完整的循环过程.
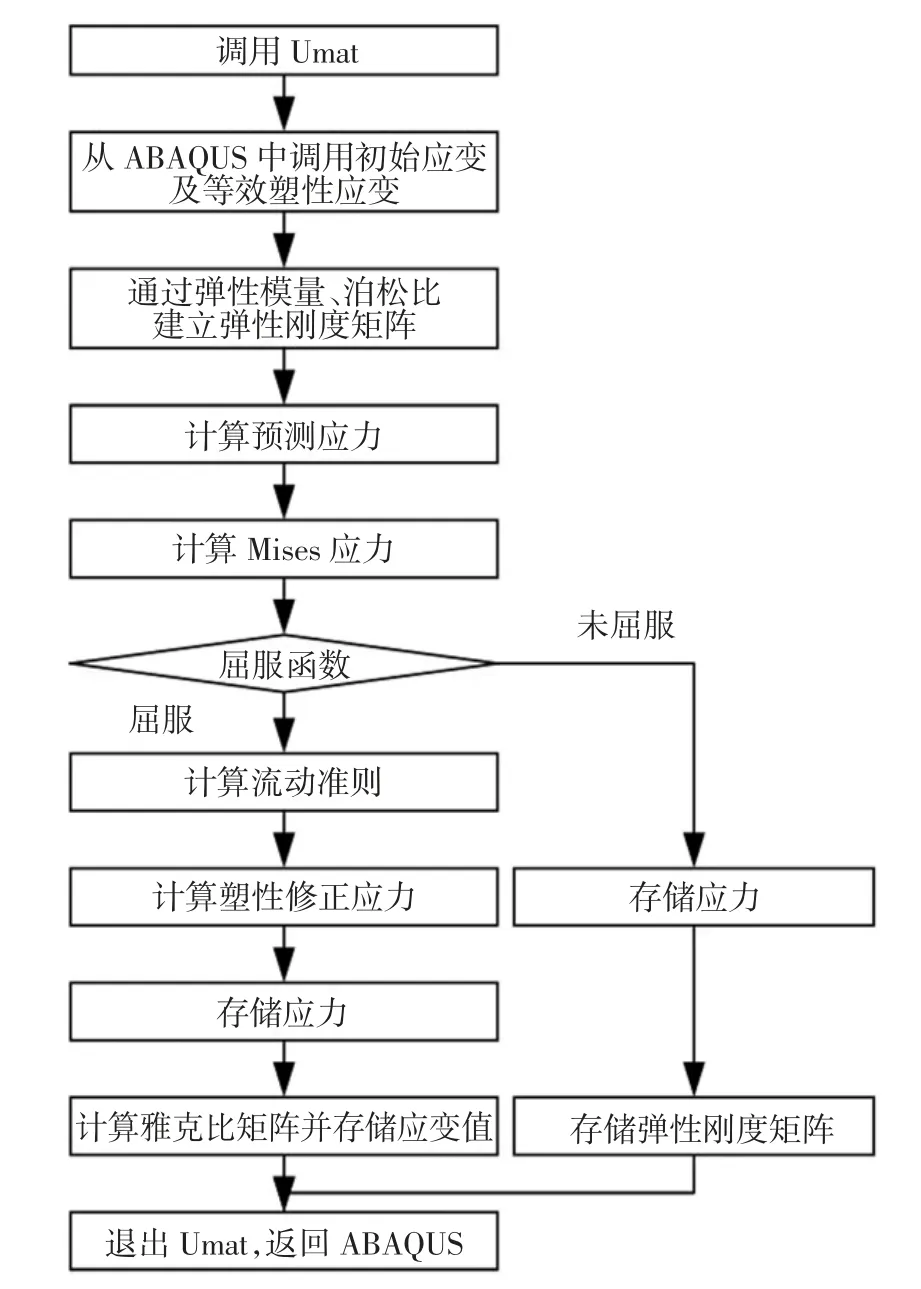
图3 子程序流程图Fig.3 The flow chart of the subroutine
利用Li 等人[29]的钢纤维混凝土受拉试验和高丹盈等人[30]的钢纤维混凝土的四点弯曲试验,分别在ABAQUS 中建立相应的有限元模型,验证本文提出的钢纤维混凝土弥撒开裂本构模型的正确性.
4.1 建立受拉试验的有限元模型
依据Li 等人[29]进行的普通混凝土及钢纤维混凝土单向受拉试验,本文利用有限元软件ABAQUS 进行了数值模拟.
首先,在ABAQUS 中建立几何尺寸为100 mm×100 mm×1 000 mm 的几何模型,通过约束模型右侧单元的自由度建立固定的边界条件,并从模型左侧进行位移加载.受拉模型的网格尺寸、边界条件及加载均如图4 所示.

图4 受拉试验的有限元模型Fig.4 The finite element model in the tensile tests
选择在ABAQUS 中建立针对钢纤维混凝土的弥散开裂本构模型;为有限元模型选择三维八节点六面体实体单元(C3D8),并采用ABAQUS 中用户自定义的材料本构模型,选用线性完全积分单元.试验中采用的钢纤维均为圆形横截面且具有高长径比,混凝土材料及钢纤维的力学性能已在表1 和表2 中具体给出.本构模型中其他参数的确定参考王金昌等人[13]:单轴与双轴的抗压强度之比为1.18,单轴抗拉与单轴抗压应力之比为0.1,双轴与单轴压应变之比为1.25,拉伸开裂应力与压缩应力之比为0.2.

表1 受拉试验中混凝土的力学性能Tab.1 Mechanical properties of concrete in tensile test

表2 受拉试验中钢纤维的力学性能Tab.2 Mechanical properties of steel fiber in tensile test
4.2 受拉试验的模型验证及数值分析
在图5 中,通过比较钢纤维混凝土和普通混凝土在受拉状态下的应力-应变曲线,可以发现数值模拟结果与试验数据均吻合良好,抗拉强度及所对应的应变值的误差均较小.能够很好地说明钢纤维对混凝土裂缝发展的控制,充分证明了本文提出的本构模型在单向受拉情况下的准确性.
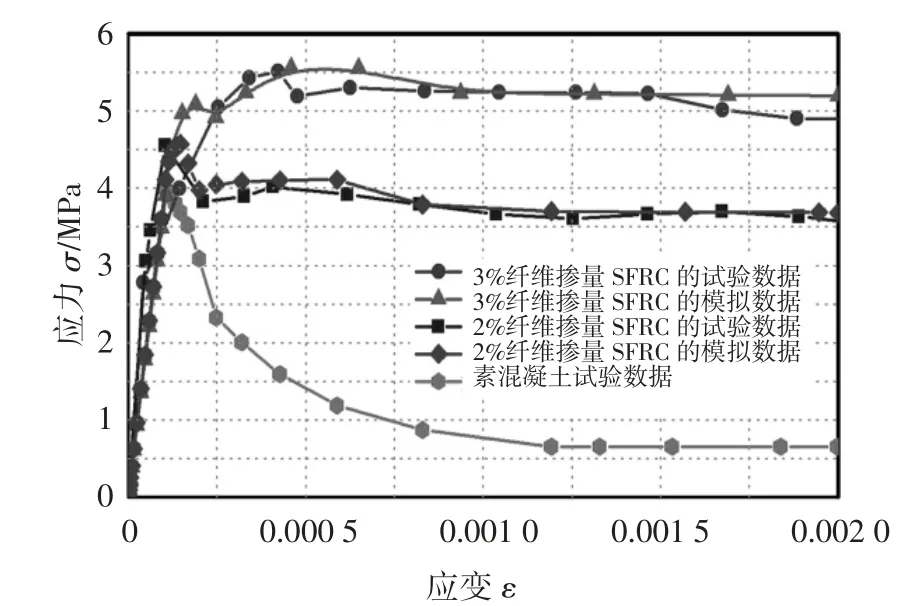
图5 钢纤维混凝土的应力-应变曲线Fig.5 The stress-strain curves of the SFRC
通过分别加入体积分数2%、3%的钢纤维,混凝土的抗拉强度从4 MPa 提高到4.75 MPa 和5.5MPa,提高了19%和37%;残余应力强度从0.65 MPa 提高到3.68 MPa 和5.2 MPa,分别提高了5.7 倍和8 倍.使混凝土在达到峰值强度后,仍保持良好的性能,纤维对混凝土的抗拉强度和残余应力均有显著的增强.
这是由于混凝土开裂后,在开裂面上的钢纤维,通过桥接作用主要承担开裂面上的应力,使混凝土在开裂后继续受拉.且随着裂缝的扩展,钢纤维与混凝土之间逐步脱黏、拔出,并在该过程中纤维持续承受拉应力.因此,相比于普通混凝土,抗拉强度及残余强度均有了显著的提高.
与普通混凝土相比,钢纤维混凝土在达到开裂强度后,应力持续增长,出现硬化,且在达到抗拉强度后应力缓慢下降,仍有较强的残余应力,说明本文所建立的本构模型充分反映了钢纤维对控制裂缝扩展的作用.
将现有模型对钢纤维掺量2%的SFRC 的受拉模拟结果,与本文所提出的本构模型以及文献中的模型的数值模拟结果进行了对比,如表3 所示.
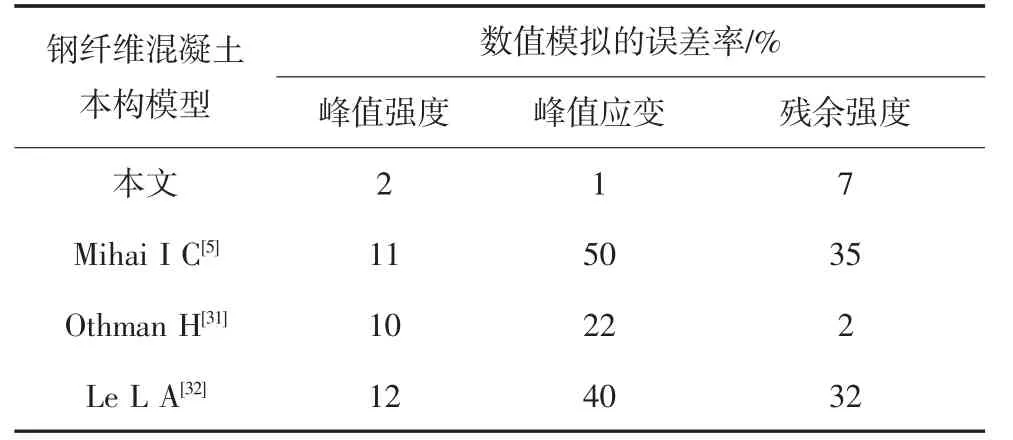
表3 数值模拟结果的准确性比较Tab.3 Comparison of accuracy in simulation results
由表3 可知,本文提出的本构模型对峰值应力和残余应力的模拟比较准确,相对误差平均值小于5%.本研究的数值模拟结果的误差处于相对较低的水平.
4.3 建立弯曲试验的有限元模型
基于高丹盈等人[30]进行的SFRC 梁的四点弯曲试验,在有限元软件ABAQUS 中建立几何尺寸为100 mm ×100 mm ×400 mm 的钢纤维混凝土梁,其中,梁跨度为300 mm;试样宽度和深度均为100 mm.试验采用长度50 mm 直径0.9 mm 的钢纤维,其中混凝土基质的力学性能如表4 所示.

表4 四点弯曲试验中混凝土的力学性能Tab.4 Mechanical properties of concrete matrix for four-points bending test
为了充分模拟弯曲试验,避免在计算过程中出现应力集中现象,在有限元模型中为SFRC 梁建立加载板和支座.通过加载板对混凝土施加竖向荷载,在支座一侧设置限制水平位移的转动边条,另一侧设置水平方向自由的转动边条.
在试验加载过程中,SFRC 梁不仅在支座处存在转动,同时存在与支座的滑移现象.因此,在模型中,对于SFRC 梁与支座和加载板之间分别建立接触,在接触面法向方向采用“硬接触”,切向方向采用摩擦理论,摩擦系数取值为0.6[27].
同样采用线性完全积分的三维八节点六面体实体单元(C3D8)来建立SFRC 梁模型.并选择在ABAQUS 中建立的针对于SFRC 的本构模型,该模型边界条件、加载情况和网格类型如图6 所示.
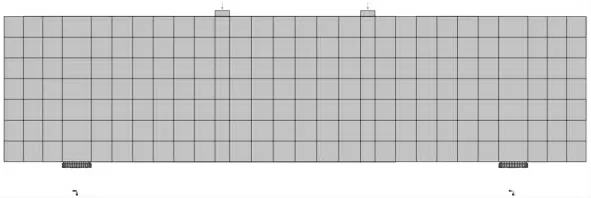
图6 四点弯曲试验的有限元模型和网格尺寸Fig.6 The finite element model and mesh size for the 4-point flexural tests
4.4 弯曲试验的模型验证及数值分析
将有限元模型模拟的SFRC 梁的四点加载试验的荷载位移曲线与高丹盈等人的试验数据进行比较,如图7 所示.荷载位移曲线中斜率的第一个转折点为SFRC 梁的开裂点,对应的荷载为SFRC 初裂荷载.有限元模拟结果与试验数据吻合良好,具体对比SFRC 的初裂荷载、荷载峰值与试验结果的误差值均在5%左右.
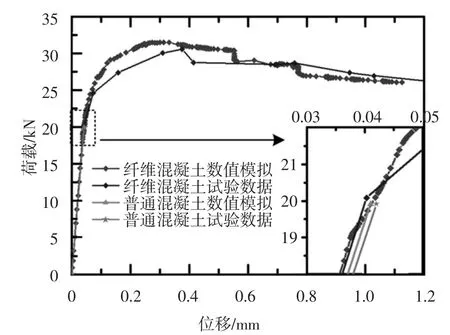
图7 纤维混凝土梁的荷载位移曲线Fig.7 The load-deformation curves of the SFRC beam
由表5 可知,在混凝土中掺入钢纤维对混凝土梁初裂荷载影响不大,普通混凝土和钢纤维混凝土梁均在荷载达到约20 kN 时,出现开裂.这与建立SFRC 的本构模型时做出的假设相吻合.普通混凝土在开裂后直接脆性破坏;而对于钢纤维混凝土,在混凝土开裂后,开裂面上的钢纤维形成纤维桥接作用,继续承担荷载,并在混凝土梁达到峰值荷载之后,仍保持较高的荷载强度.
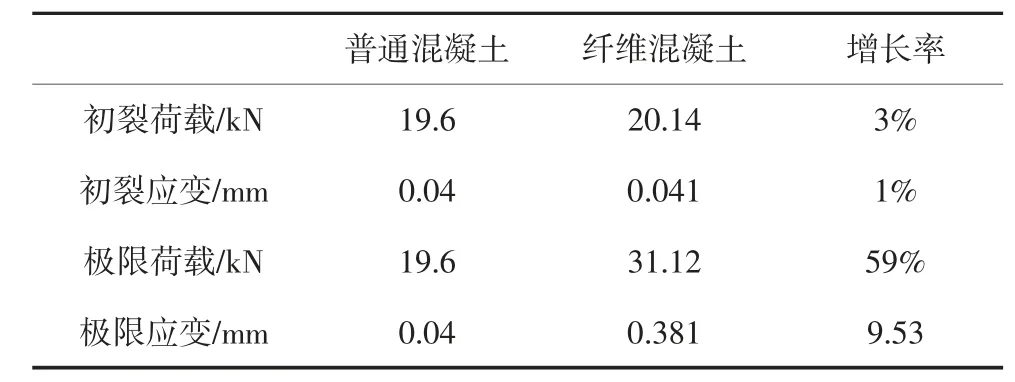
表5 弯曲试验的荷载与挠度值Tab.5 Load and deflection of the bending test
基于ASTM C 1609[33],计算钢纤维混凝土梁在四点弯曲试验中的抗弯强度如公式(19)所示.

式中:fflex和P 分别为SFRC 梁的抗弯强度和荷载;L、b 和h 为梁的跨度、宽度和深度.
在图8 中分别给出了钢纤维混凝土梁和普通混凝土梁的强度-位移曲线.钢纤维的掺入使混凝土的抗弯强度由6 MPa 提高到9.4 MPa,增强幅度超过50%.

图8 纤维混凝土梁的应力位移曲线Fig.8 The stress-deflection curves of the SFRC beam
根据ASTM C1018 规范中所采用的韧性指数,分别对普通混凝土和钢纤维混凝土的韧性进行了评估[34],具体如公式(20):

式中:TI 是混凝土韧性指数;δ0是峰值所对应的的挠度值,Ωδ0和Ω3δ0分别是在δ0和3δ0时荷载位移曲线下所包含的面积,如图9 所示.
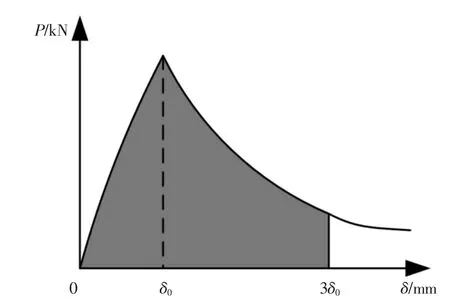
图9 混凝土韧性计算的示意图Fig.9 Schematic diagram of the concrete toughness
如表6 所示,钢纤维对混凝土增强的作用不仅是SFRC 的承载和变形,同时对混凝土的韧性有显著的增强作用.
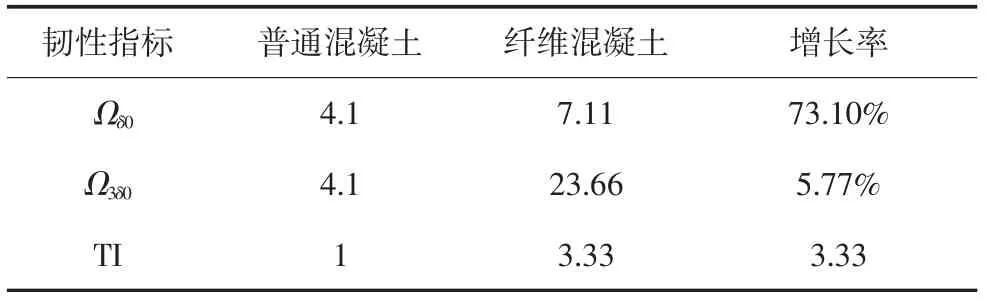
表6 受拉试验中钢纤维混凝土的韧性Tab.6 Toughness of SFRC in the tensile tests
钢纤维混凝土梁的纯弯部分在梁高方向出现了显著的变形,如图10 所示.整个纯弯部分向下挠曲变形,整个混凝土梁通过支座发生扭转,支座两侧部分出现少量的抬高.
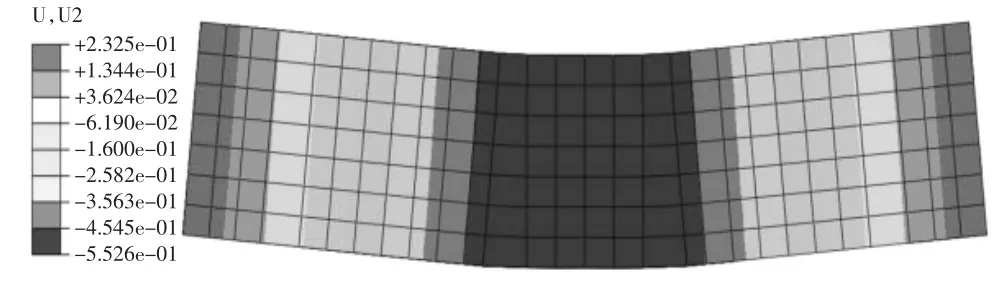
图10 SFRC 梁的挠度变形Fig.10 The deformation of the SFRC beam
图11 给出了钢纤维混凝土梁在不同荷载阶段梁长方向的应力云图.在整个加载过程中SFRC 梁中的压应力始终小于SFRC 的抗压强度,因此,SFRC梁中受压作用部分均用深灰色表示.
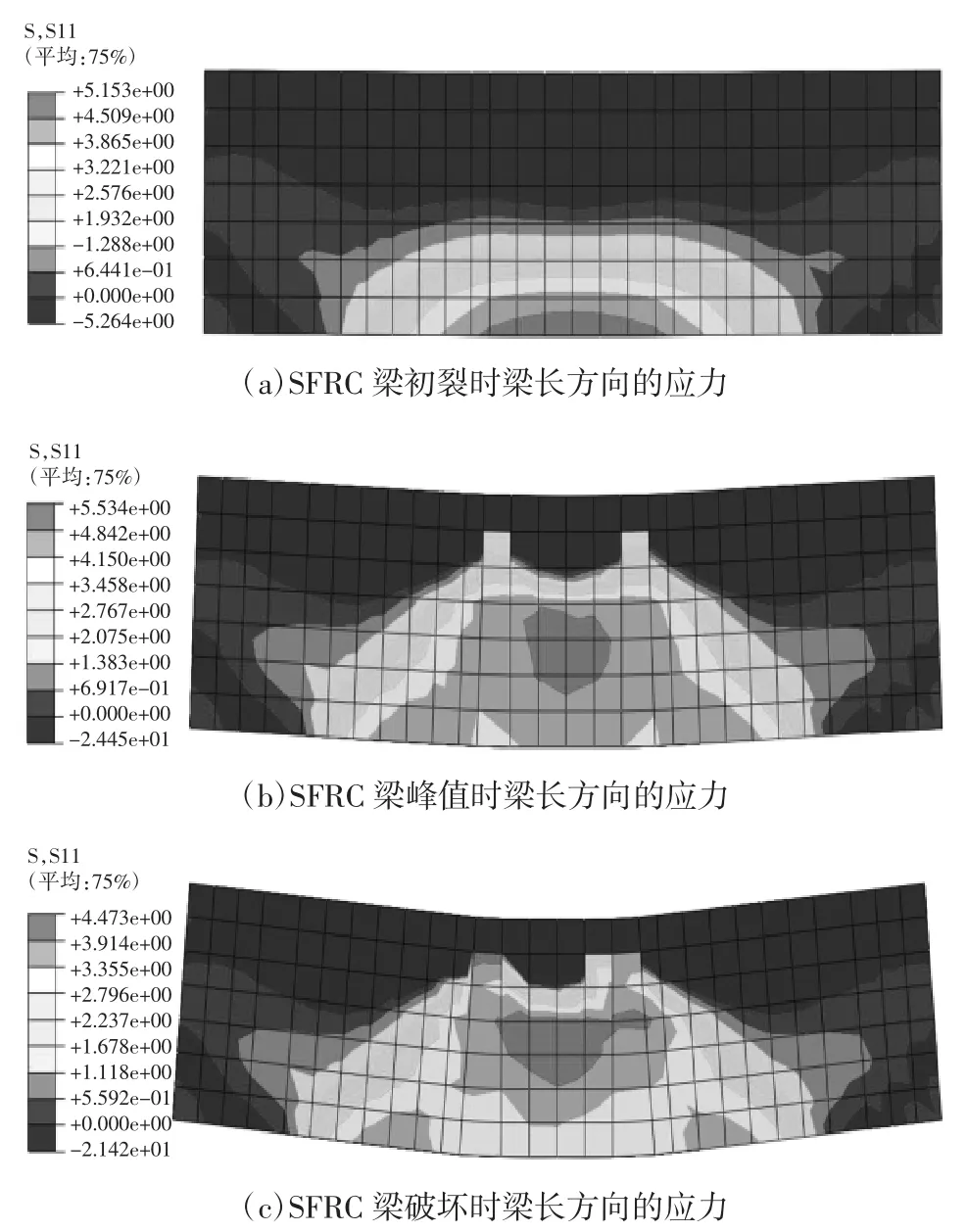
图11 SFRC 梁的应力分布Fig.11 The stress profiles of the SFRC beam
由初裂时刻仅在纯弯段底部最下层应力达到混凝土抗拉强度,其他部分的拉应力值较小,同时梁上侧混凝土处于受压状态;在荷载达到峰值时,梁大部分处于受拉状态,中性轴明显上移,最大应力的位置从最下层上移,SFRC 梁底部的钢纤维混凝土进入了塑性软化阶段;在SFRC 梁最终破坏时,最大应力的位置继续上移,裂缝进一步扩展.
随着荷载的施加,钢纤维混凝土梁塑性应变量随之变大,塑性变形范围也相应增大,如图12 所示.在SFRC 梁的初裂时刻,仅在纯弯段底部最下层出现塑性变形;当达到荷载峰值后,SFRC 梁的纯弯段中大部分都已进入塑性阶段.
如图13 所示,在纯弯段部分混凝土梁开裂后,在纤维桥接作用下,纤维混凝土应力增强,达到应力峰值后,进入软化段直至钢纤维混凝土梁破坏.
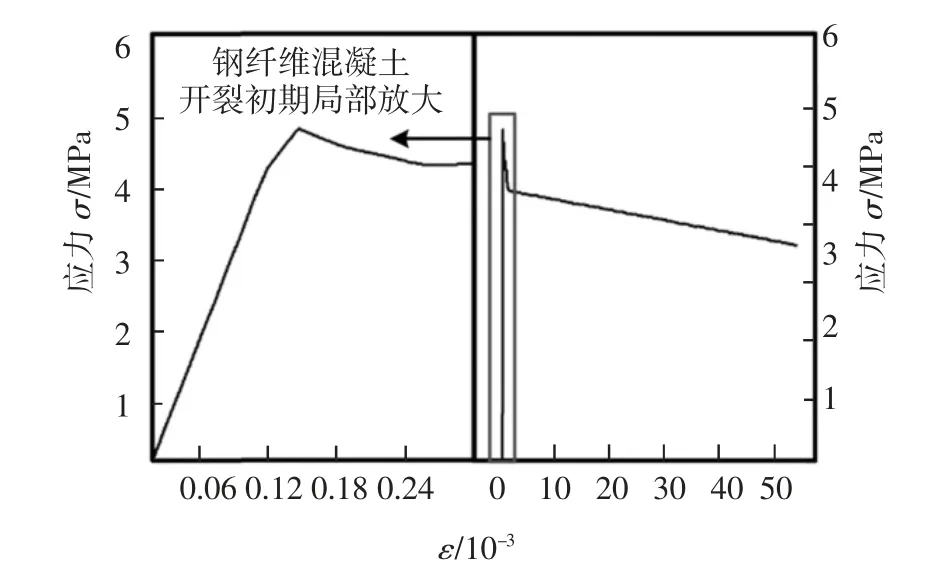
图13 钢纤维混凝土主裂缝处的应力-应变图Fig.13 Stress-strain diagram of mainly cracked in SFRC
5 结论
本文基于普通混凝土的弥散开裂模型,并考虑在混凝土开裂后,钢纤维与混凝土界面脱黏过程以及钢纤维在混凝土拔出过程,提出了一种钢纤维混凝土的弥散开裂本构模型.
通过Fortran 编程和ABAQUS 子程序接口Umat,将本文提出的钢纤维混凝土本构模型引入到ABAQUS 的材料库中.基于单向受拉试验和四点弯曲试验,分别建立有限元模型,并通过对比试验数据和有限元的数值模拟结果,充分验证了本文所提出的钢纤维混凝土本构模型的准确性.
基于单向受拉试验的数值模拟,加入钢纤维对混凝土抗拉强度和残余强度均有显著的增强作用,使混凝土在达到峰值强度后,仍具有良好的力学性能.钢纤维混凝土在达到开裂强度后,由于开裂面上钢纤维的桥接作用,钢纤维混凝土开裂后应力持续增长出现硬化,在达到抗拉强度后缓慢下降.
在四点弯曲试验的模拟中,纤维加入大幅度提高了混凝土的弯曲强度,有效地改善了混凝土韧性的不足.同时,通过对比试验数据和数值模拟的开裂荷载,验证了在本构模型建立时,忽略钢纤维对混凝土初裂强度影响的合理性.
