破片与冲击波复合作用下预应力混凝土T 形梁损伤分析

2021-07-25田力王赛

湖南大学学报（自然科学版） 2021年7期

田力，王赛

（1.天津大学建筑工程学院，天津 300072；2.滨海土木工程结构与安全教育部重点实验室（天津大学），天津 300072）

由于预应力相关工程技术的创新和完善，预应力钢筋混凝土桥梁构件被越来越多地应用到大跨度桥梁工程建设中.预应力钢筋混凝土T 形梁由于其自身的结构特性，能有效利用现代化高强度钢绞线和高强混凝土，从而减小构件截面尺寸，显著降低结构自重占全部设计荷载的比重，提高结构构件耐久性，增加构件跨度.然而，当今国际形势复杂多变，地区冲突及恐怖袭击时有发生，全球各地发生的爆炸袭击事件和意外爆炸事故仍然历历在目，倘若预应力钢筋混凝土T 形梁因此损毁，将对人民生命财产安全和经济社会稳定发展带来重大损害.因此对预应力T 形梁的抗爆性能开展研究具有重要的实际应用价值.由于预应力T 形梁相关抗爆实验费用高昂，对试件损伤的观察不连续，且存在安全隐患，因此数值模拟方法特别受到重视.

迄今为止，国内外学者对预应力钢筋混凝土构件在单一冲击波荷载作用下的抗爆分析探究较多.李砚召等[1]在平面装药爆炸条件下，对后张无黏结部分预应力混凝土梁板柱形结构开展大比尺化相似模拟试验，分析得出预应力混凝土梁板柱形结构拥有良好的延性.娄凡[2]对承受爆炸波作用的两跨预应力混凝土连续T 形梁桥的动力响应特征及破坏模式，进行了试验及数值模拟探究，指出当梁跨中正上方发生爆炸时，梁发生局部冲切破坏.刘云飞等[3]利用ANSYS/LS-DYNA 软件对核电站预应力钢筋混凝土安全壳在内爆作用下进行了数值模拟，揭示了内爆作用下结构薄弱部位的应力集中现象.Cofer 等[4]对预应力钢筋混凝土T 形梁桥开展了爆炸试验并采用ABAQUS 软件进行了数值模拟对比研究，指出了跨中桥面上方发生爆炸会对梁产生严重的局部损伤.Choi 等[5]对在近距爆炸荷载作用下的无钢筋预应力混凝土板和有钢筋预应力混凝土板开展了试验与数值模拟对比研究，得到了预应力对增强混凝土板抗爆性能的影响规律.Chen 等[6]基于ANSYS/LS-DYNA软件，对爆炸荷载作用下的预应力RC 梁进行了数值模拟，分析得出预应力能有效延缓混凝土挠曲裂纹的出现和扩展，但提高预应力可能会发生梁支撑附近的斜向剪切损伤.然而目前，国内外学者对较大尺寸的预应力钢筋混凝土T 形梁受冲击波-破片群复合作用的抗爆研究非常有限，而破片群对构件的侵彻作用增强了爆炸物的毁伤威力，因此实际工程应用中应对冲击波-破片群复合荷载给予格外的重视.

截至目前，涉及到预应力钢筋混凝土T 形梁曲线形预应力筋的数值模拟基本是单根或多根二维平面内弯曲的，对于预应力筋是三维空间内弯曲的预应力钢筋混凝土T 形梁，在破片和冲击波复合作用下的损伤研究几乎处于空白阶段，因此对它的研究意义重大.本文利用有限元软件ANSYS/LS-DYNA先通过数值模拟与已有试验实测数据对比分析，验证了该数值模拟方法的有效性.分别对冲击波、破片群及二者复合作用3 种工况开展数值模拟，并分析预应力钢筋混凝土T 形梁的变形、受力和损伤效应.基于参数化分析方法，模拟分析张拉控制应力、混凝土强度、配筋率等因素对预应力钢筋混凝土T 形梁的抗爆性能影响.

1 有限元模型及数值分析方法

1.1 模型介绍

建立预应力钢筋混凝土T 形梁在冲击波-破片群复合作用下的有限元模型，如图1 所示.预应力钢筋混凝土T 形梁全长1 690 cm，上翼缘宽度为150 cm，翼缘板边缘厚度为16 cm，二者全长保持不变.腹板为变截面形式，梁两端各有长度215 cm 的部分为横截面形式不变段，截面横向宽度为48 cm，截面配筋及尺寸见图2（a）.梁中段长度为1 160 cm 的部分腹板厚度为24 cm 且保持不变，截面配筋及尺寸见图2（b）.梁中段腹板两端各存在一段长度30 cm的截面渐变段，该段通过实体单元逐层递减的方式实现腹板横截面尺寸渐变.同理，在T 形梁中部腹板与底部马蹄衔接处同样采用实体单元逐层递减的方式实现二者之间的尺寸渐变，马蹄部分宽度为48 cm.T 形梁两侧各有4 块钢筋混凝土隔板，根据其实际受力及变形情况，在隔板端界面设置相应约束，借鉴黄飞[7]基于弥散钢筋的方法，暂不考虑隔板内钢筋的作用，通过定义关键字 *MAT_JOHNSON_HOLMQUIST_CONCRETE，并适当增大混凝土破坏强度，借以弥补不考虑钢筋致使隔板整体强度下降的问题.本文通过利用多段折线来近似代替曲线形预应力钢绞线，其中，预应力钢绞线N1 在x-Oy 二维坐标平面内弯曲，预应力钢绞线N2、N3 在xy-z 三维坐标空间内弯曲.考虑到所研究的预应力钢筋混凝土T 形梁采用后张法有黏结方式施加预应力，本文不考虑钢绞线与混凝土间的黏结滑移作用，预应力钢绞线采用与混凝土耦合节点的方式传递应力应变，预应力钢绞线抗拉强度标准值ftpk=1 860 MPa.普通钢筋选用HRB335，采用与混凝土单元共节点处理.由于实际结构在梁两端处细部构造复杂，同时考虑主要受力及变形情况，本文将梁两端采用简支约束方式.考虑到隔板起着加强各根主梁间的横向联系增强结构整体性、提升主梁的横向刚度和稳定性以及提高梁体的抗扭刚度等作用，故隔板对梁体沿z 轴的侧向移动以及绕x 和y轴的转动起到了突出的约束作用，而对其他自由度的约束相对较弱.综上，基于实际工程情况，对隔板的端界面约束进行合理的简化处理，在其上施加沿z 轴的平动自由度约束以及分别绕x 轴和y 轴的转动自由度约束.

图1 预应力钢筋混凝土T 形梁有限元模型Fig.1 Finite element model of a prestressed reinforced concrete T-beam

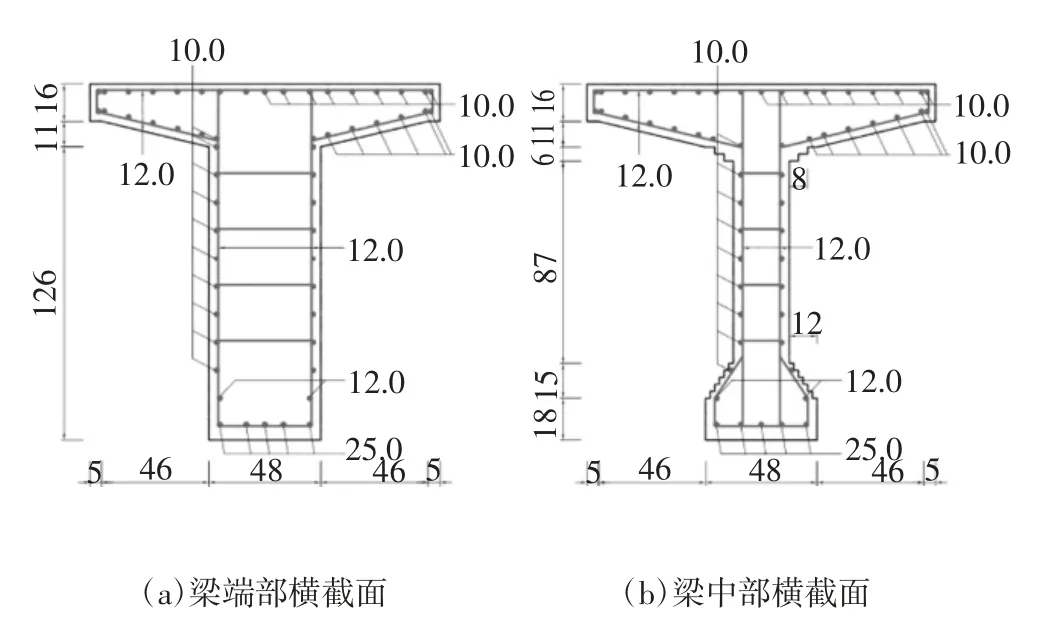
图2 梁横截面配筋及尺寸图（单位：mm）Fig.2 Cross-section reinforcement and dimension chart of T-beam（unit：mm）

炸药选用铵油（ANFO），尺寸为44 cm×44 cm×44 cm，质量为79.2 kg.由于本文中起爆点位于梁上方，炸药底侧破片在飞散过程中对结构物作用明显，而其他侧的破片飞散出去后对结构几乎无作用，因此本文只在炸药底侧布置破片.破片尺寸为2 cm×2.5 cm×2 cm.综合考虑时间成本和模拟效果，经反复试算，取空气域尺寸为220 cm×258.5 cm×156 cm，空气域边界面设置无反射边界条件.混凝土、锚具、底部支撑、炸药、破片和空气选用SOLID164 单元，钢绞线及钢筋选用BEAM161 单元.混凝土单元最大尺寸为3 cm，炸药单元尺寸为3 cm，空气单元尺寸为4 cm.混凝土单元数约为82 万，钢绞线及钢筋单元数共计约为7 万，隔板单元数约为4.3 万，空气和炸药单元数共计约17.4 万.

1.2 数值分析方法

T 形梁、空气、破片群和炸药之间的流固耦合相互作用的数值模拟，通过罚函数耦合算法来实现.破片群和T 形梁之间定义侵蚀接触，破片之间定义自动单面接触，时间步长比例因子取为0.67.考虑到避免采用单点积分所带来的沙漏模式，选用刚性沙漏控制方法，沙漏系数取0.03.数值分析过程共分两个阶段，即应力初始化阶段和冲击波-破片群复合作用阶段.

第一阶段（应力初始化阶段）：该阶段通过在T形梁上设置重力加速度的方式以达到施加重力荷载的目的.基于降温法使得钢绞线单元收缩，以此对混凝土施加张拉控制应力.采用关键字*CONTROL_DYNAMIC_RELAXATION 对此阶段进行控制，通过能量收敛准则判断T 形梁的平衡状态[8]，使结构在第二阶段开始前达到稳定状态.

第二阶段（冲击波-破片群复合作用阶段）：将T形梁在第一阶段末的应力应变状态作为第二阶段分析的初始状态，计算分析T 形梁在冲击波-破片群复合作用下的损伤状况及位移动力响应.综合考虑计算效果及时间成本选取计算时长[9].

1.3 材料本构模型

混凝土本构模型选用*MAT_CONCRETE_DAMAGE_REL3，此模型结合所定义的应变率曲线，能有效地考虑混凝土强度在不同应变率下的增强效应[10]，且混凝土单元应变率越大混凝土强度增强效应越明显，密度2 500 kg/m3，弹性模量3.63×104MPa，泊松比0.2，混凝土轴心抗压强度40 MPa.为避免计算全过程中因大变形导致混凝土单元负体积和畸形单元的出现，同时模拟真实工况下混凝土的压碎与剥落，将*MAT_ADD_EROSION 定义为其失效准则，参考文献[11]，并经多次试算验证，失效主应变取0.27，模拟效果最佳.

钢绞线采用*MAT_ELASTIC_PLASTIC_THERMAL 本构模型，密度7 800 kg/m3，弹性模量1.95×105MPa，泊松比0.3，屈服强度1 630 MPa.该模型模拟了材料各力学性能与温度变化的关系，同时结合定义的温度变化曲线，用降温法实现钢绞线的热胀冷缩，从而对混凝土施加预应力.

由于普通纵向钢筋及箍筋在数值模拟过程中处于高应变率状态，因此两者均采用*MAT_PL-ASTIC_KINEMATIC 本构模型，密度7 800 kg/m3，弹性模量2.06×105MPa，泊松比0.3，屈服强度335 MPa，其余材料模型参数参见文献[12].

铵油（ANFO）炸药采用*MAT_HIGH_EXPLOSIVE_BURN 模型及JWL 状态方程[13-14]描述，表达式为：

式中：P 为炸药爆轰压力；A 和B 为材料常数；R1、R2和ω 为试验拟合参数；V 为相对体积；E0为炸药单位体积的初始内能，其参数值详见表1.

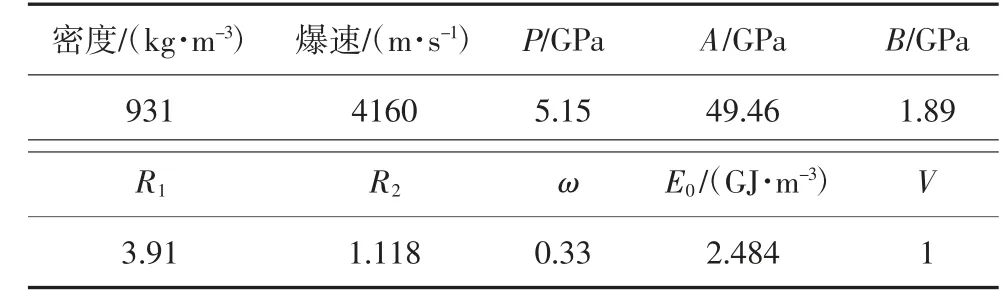
表1 铵油（ANFO）炸药参数Tab.1 Material properties of ANFO

空气采用*MAT_NULL 模型及*EOS_LINEAR_POLYNOMINAL 状态方程描述，其表达式为：

式中：pa为压力；C0～C6均为用户自定义常数；E0为单位体积初始内能；μ=-1 指相对体积.表2 列出了其参数值.

表2 空气参数Tab.2 Material properties of air

建立隔板部分数值模型时，采用弥散钢筋的方法直接对隔板钢筋混凝土整体建模，选用*MAT_JOHNSON_HOLMQUIST_CONCRETE 模型，经多次试算，材料参数取为：密度2 550 kg/m3，剪切模量1.7×104MPa，弥散钢筋后混凝土准静态单轴抗压强度60 MPa，该模型适用于承受大应变、高应变率和高压的混凝土工况[10].通过适当提高混凝土材料强度及密度，以弥补不考虑钢筋所带来的承载力降低问题.引入失效准则，以便控制大变形可能产生的单元畸变，失效主应变取0.27.

破片材料采用钨合金，考虑计算时间成本，破片取为刚体材料，忽略计算全过程中的变形及损伤，故采用*MAT_RIGID 模型，参阅文献[15]，密度为17 800 kg/m3，弹性模量为357 GPa，泊松比为0.303，破片质量为178 g.

2 数值模拟有效性验证

考虑到目前国内外对于冲击波-破片群复合作用下预应力钢筋混凝土T 形梁的试验研究还处于空白阶段，因此本文分3 个部分从不同角度验证所用有限元模拟方法的有效性.首先，开展预应力钢筋混凝土板在单独冲击波作用下的试验有限元模拟，验证了流固耦合算法及材料本构模型的有效性.其次，对落锤作用下预应力混凝土梁试验进行数值模拟，检验了用多段折线模拟曲线形预应力筋处理方法的可靠性.最后，模拟破片群作用下钢筋混凝土板的侵彻试验，并与试验数据对比，验证了破片飞散速度及侵彻深度的数值模拟参数的合理性.2.1 节和2.2 节所建立的有限元模型分别为无黏结预应力钢筋混凝土板和无黏结预应力混凝土梁，预应力筋单元与混凝土单元之间不进行耦合节点处理，而是分别建立混凝土预制孔道和预应力筋有限元模型，并通过在预应力筋与混凝土之间设置关键字*CONTACT_AUTOMATIC_BEAMS_TO_SURFAC -E 来模拟预应力筋与混凝土孔道壁之间的接触传力.

2.1 冲击波作用下预应力钢筋混凝土板试验验证

Choi 等[5]分别对近爆冲击波作用下的钢筋混凝土板（RC）、无钢筋预应力混凝土板（PSC）B 型与D型及预应力钢筋混凝土板（PSRC）B 型与D 型进行了抗爆性能及动态响应研究.本文选取预应力钢筋混凝土板（PSRC）D 型的工况进行数值模拟验证.

试验中预应力钢筋混凝土板（PSRC）D 型采用后张无黏结法施加预应力，钢绞线屈服强度为2 040 MPa，极限强度为2 400 MPa，单位质量为1.101 kg/m，每股6 根.混凝土抗压强度为40 MPa.板的迎爆面和背爆面各有一层钢筋网，钢筋直径为13 mm，钢筋中心间距为100 mm，钢筋网与板表面的间距为50 mm.板放在置于地下的钢架上，板四周用钢板壳固定.25 kg ANFO 炸药位于板中心点上方1 m 处并悬挂在木架上.板的配筋如图3 所示.

依据试验实际工况建立数值模型，单元类型、材料本构、接触设置和耦合算法均与第1 节相同，板背爆面中点竖向位移以向下为负.

图4 为D 型PSRC 板背爆面中点竖向位移时程曲线图，由图4 可知板背爆面中点竖向位移数值模拟峰值为-7.88 mm，由文献[5]可知相应的峰值位移试验实测值为-7.96 mm，两者相对误差为1.01%，位移峰值模拟精度很高.从图可见板背爆面中点竖向位移数值模拟峰值出现时间与试验值相比较早，考虑到数值模拟时试件四周钢板壳对试件的约束效果是理想状况，而实际试验中试件会受到人为安装操作误差等不确定因素影响，以及实际炸药外形并不是理想的长方体，因此以上因素会对板背爆面中点竖向位移数值模拟峰值出现时间有一定的影响，但数值模拟中位移时程曲线的变化态势及最终位移值与试验测试结果基本相同，因此本文所采用的流固耦合算法及材料模型能较准确地模拟炸药冲击波对预应力试件的破坏作用.

2.2 预应力混凝土梁落锤冲击试验验证

李砚召[16]等对3 根无黏结部分预应力混凝土梁开展了落锤冲击试验，并测试其动态位移响应与极限承载力.本文选取落锤质量为90 kg、下落高度H=5 m 的工况进行有限元模拟验证.

试验梁尺寸长×宽×高为2 600 mm×220 mm×160 mm，选用C50 强度等级混凝土，截面受拉区配筋为2ϕ12，受压区配筋为2ϕ8，箍筋配筋为ϕ6＠100，保护层厚度为20 mm.钢绞线抗拉强度为1 860 MPa（与1.1 节所述钢绞线相同），形式为开口向上的抛物线，最低点处保护层厚度为40 mm，两端穿过端截面形心.试件配筋见图5.

图5 试件配筋图（单位：mm）Fig.5 Reinforcement diagram of test piece（unit：mm）

图6 为试验梁底部跨中位移时程曲线实测值与模拟值对比图，由图6 可知梁跨中峰值位移模拟值为45.2 mm，文献[16]中与其对应的实测值为46 mm，误差为1.74%，由此可知峰值位移模拟精度很高.此外位移时程曲线模拟值与实测值在上升阶段几乎一致，在下降阶段二者走势相同，且在t=40 ms 时数值吻合较好.图7 显示了试件跨中上表面混凝土压应变时程曲线对比情况，数值模拟所得的试件跨中上表面混凝土压应变峰值为4.52×10-3，参阅文献[16]可知其实测值约为4.42×10-3，相对误差为2.26%，故二者吻合良好.经观察可知二者整体变化规律和态势一致，模拟效果较好.综上，本节验证了用多段折线模拟曲线形预应力筋处理方法的可靠性.

图6 梁跨中位移Fig.6 Displacement of beam’s middle

图7 梁跨中上表面混凝土压应变Fig.7 Concrete’s compressive strain on top surface of beam’s middle

2.3 破片群对混凝土板侵蚀试验验证

Linz[17]等对不同尺寸钢筋混凝土板开展了在冲击波-破片群复合作用下的抗爆试验，获得了破片群对混凝土板的侵彻及损伤实物和实测数据.本节对其中板厚为10 cm 的工况进行数值模拟验证.

由文献[17]可知试验板尺寸为：长160 cm，宽80 cm，厚10 cm，板中有上下两层钢筋，钢筋直径均为6 mm，钢筋长向间距200 mm，短向间距150 mm，上层钢筋保护层厚度20 mm，下层钢筋保护层厚度16 mm.TNT 炸药位于板中心点上方2.1 m 处，形状是直径及高度均为200 mm 的圆柱，炸药底部附有346 个直径为8 mm 的钢球.

经有限元数值模拟所得到的破片速度时程曲线见图8.破片对混凝土板的侵彻作用全过程分3 个阶段，炸药驱动破片使其速度猛然增加，经过空气中的飞散阶段后破片到达试件表面，此后破片开始侵彻试件，同时破片速度急剧减小，最后趋于稳定.由计算结果可得破片到达板表面时的速度为1680.63 m/s，参阅文献[17]可知相应试验实测值范围为1 650～1 780 m/s，因此破片侵彻速度数值模拟结果十分吻合.图9 为破片侵彻深度数值模拟塑性应变云图，破片侵彻深度模拟值为24.1 mm，文献[17]中所述试验测量值范围为20～25 mm，故破片侵彻深度模拟效果精确度很高，同时验证了破片飞散速度及侵彻深度的数值模拟参数的合理性.

图8 破片速度时程曲线Fig.8 Speed time history curve of fragment

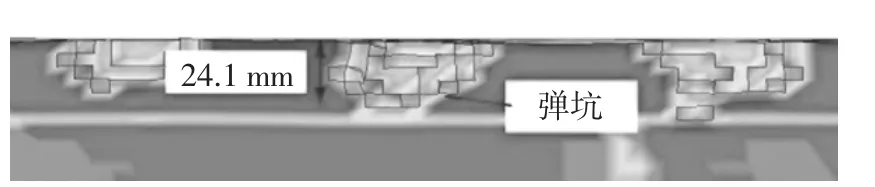
图9 试件塑性应变云图Fig.9 Plastic strain cloud diagram of specimen

3 冲击波作用、破片群作用及二者复合作用对预应力T 形梁的损伤分析

为探究预应力T 形梁分别在冲击波单独作用、破片群单独作用及二者复合作用下的损伤和位移响应，本节共分3 种工况分别进行有限元数值模拟对比分析，详见表3.预应力T 形梁的配筋方式与1.1节所述相同.

表3 数值模拟工况Tab.3 Numerical simulation conditions

3.1 变形与损伤对比分析

GK-1 中梁的塑性应变云图见图10（a），由图可知冲击波产生的空气超压使T 形梁中段上翼缘板产生明显较平滑的向下弯曲渐变曲面，同时只在翼缘板上表面个别点位处及翼缘板下表面局部产生破损.此外，由于爆炸冲击作用，腹板中产生的拉应力流使梁在梁长方向关于中心对称的两侧腹板中出现斜向高应变带，而梁整体并无明显破坏现象.产生上述现象的原因是，炸药爆炸后会产生近似球面的冲击波并向四周传播，冲击波波阵面与翼缘板接触面较大，处于炸药爆心正下方的梁翼缘板板面所受冲击波超压最大，同时，冲击波超压向两端递减.

图10（b）所示为GK-2 中梁的塑性应变云图，由于该工况下只考虑破片群单独作用（即只在空气与破片群间定义流固耦合关键字，空气与梁间不定义流固耦合关键字），因此数值模拟过程相当于破片群对试件的撞击和侵彻作用，因此梁中段部分的上翼缘板及腹板都有明显侵彻破坏现象，同时因为不考虑冲击波作用，故在梁上翼缘板的损伤段并没有产生较平滑的向下弯曲渐变曲面.

GK-3 中梁的塑性应变云图见图10（c），由图可知，在炸药正下方的梁区段内，上翼缘板和腹板均有明显破坏现象，但相对于GK-2 梁损伤程度略微较轻，产生此现象的原因是：当考虑冲击波与破片群复合作用时，冲击波与T 形梁之间存在相互作用，冲击波波阵面到达梁上表面后会发生反射，反射部分的冲击波会对破片群起到一定程度的阻碍作用，使破片到达梁上表面时的动能与GK-2 相比较低，故破片群的侵彻作用相对减弱，由于冲击波的存在，使梁上翼缘板同时承受冲击波球形波阵面冲击作用和破片群侵彻作用，因此相较GK-2，GK-3 中梁中段部分的翼缘板及腹板既有明显侵彻破坏现象，又产生较平滑的向下弯曲渐变曲面.

图10 试件塑性应变云图Fig.10 Plastic strain cloud diagram of specimen

3.2 位移响应对比分析

图11 为GK-1、GK-2、GK-3 三种工况下T 形梁底部中点O 竖向位移时程曲线对比图（位移方向以竖直向下为负）.考虑到研究目的是探究前20 ms 内T 形梁，分别在GK-1、GK-2、GK-3 三种工况下初始阶段瞬时位移动态响应间的大小关系，加之计算时间成本较为高昂，故取20 ms 时的位移为峰值位移，进行位移动态响应对比分析.由图11 可知，冲击波单独作用下梁底部中点O 竖向位移峰值为-29.83 mm；破片群单独作用时，梁底部中点O 竖向位移峰值为-33.59 mm，明显大于GK-1 中相应数值，相对增加幅度为12.6%，这是因为冲击波单独作用时，梁并无明显破坏，而在破片群单独作用下，梁中部翼缘板及腹板处的混凝土、纵向钢筋和箍筋均破坏较严重，使得梁横截面抗弯和抗剪刚度明显减小，梁的承载能力降低，因此GK-2 中的位移峰值大于GK-1.二者复合作用下梁底部中点O 竖向位移峰值为-40.5 mm，大于GK-1 和GK-2 的情况，相对GK-1 增加35.43%，相较于GK-2 增幅为20.27%.由此可见，冲击波和破片复合作用下，T 形梁的竖向位移动态响应峰值大于两种荷载单独作用时的工况.参阅文献[18]可知，冲击波-破片复合作用时，冲击波比破片群先到达梁表面，而冲击波驱动破片过程中会受到破片群的阻挡而发生绕流现象，导致冲击波作用在梁表面的超压峰值相较GK-1 减弱，反射的冲击波使到达梁表面的破片群动能相较GK-2减小，因此导致冲击波-破片对梁的复合作用效果小于两种荷载单独作用效果的线性叠加.此外由图11可见在7.5～10.0 ms 间GK-1 位移时程曲线下降速度快于GK-2 和GK-3，原因是GK-1 中梁无明显毁伤，冲击波超压与梁接触作用很充分，故位移增加速率较快，GK-2 和GK-3 中由于破片群的侵彻作用，使梁翼缘板损伤严重，翼缘板混凝土剥落显著，因此，冲击波超压会从T 形梁翼缘板破损处透过，使得冲击波波阵面与梁上表面接触面积减小，作用力降低，故其位移增加速率较慢.综上可知，冲击波-破片对T 形梁的复合作用效果大于单一荷载作用效果，但小于两种荷载单独作用效果的线性叠加，故对预应力T 形梁进行抗爆设计时，要考虑冲击波-破片群复合作用的实际工况.

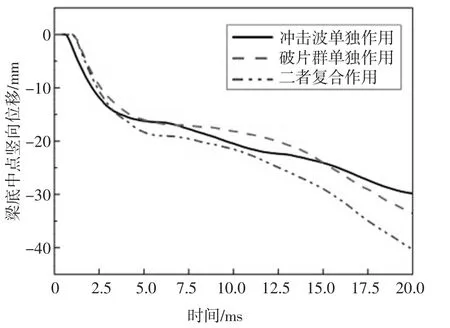
图11 梁底中点O 位移时程曲线Fig.11 Time-history curve of midpoint O displacement at the bottom of the beam

4 冲击波-破片群复合作用下预应力T 形梁的参数化分析

4.1 预应力筋的张拉控制应力

预应力筋的张拉控制应力的大小直接影响着T形梁横截面初始应力分布状态，进而影响T 形梁的极限承载力及变形能力.因此为研究张拉控制应力大小对冲击波-破片复合作用下预应力T 形梁的抗爆性能影响，本节分别对张拉控制应力等于0.75ftpk、0.65ftpk、0.55ftpk、0.45ftpk、0.00ftpk（预应力钢绞线抗拉强度标准值ftpk=1 860 MPa）的5 种工况分别开展数值模拟分析计算，所得T 形梁底部中点O 竖向位移时程曲线对比图、梁底面纵向中轴线A-A 上各点位移包络图（在梁底面纵向中轴线A-A 上每隔205 cm选取一点为本文后续研究梁底面A-A 位移包络图使用）及梁底面横向中轴线B-B 上各点位移包络图（在梁底面横向中轴线B-B 上每隔6 cm 选取一点为本文后续研究梁底面B-B 位移包络图使用）见图12（位移以向下为负）.

由图12（a）可知，张拉控制应力为0.75ftpk时，梁底中点O 竖向位移峰值为-4.05 cm；0.65ftpk时，其值为-4.53 cm，相较0.75ftpk增加11.85%；0.55ftpk时，位移峰值为-4.77 cm，相较0.75ftpk增加17.78%；0.45ftpk时，位移峰值为-4.93 cm，相较0.75ftpk增加21.73%；0.00ftpk时，其值为-6.82 cm，相较0.75ftpk增加68.4%，可见在0.00ftpk～0.45ftpk之间提升张拉控制应力值可以十分显著地提高T 形梁的抗弯刚度，减小梁底中点O 竖向位移峰值；在0.45ftpk～0.65ftpk之间提升张拉控制应力值时，T 形梁的抗弯刚度有一定的提升但并不明显；在0.65ftpk～0.75ftpk之间提升张拉控制应力值时，T 形梁的抗弯刚度提升较为明显.另外，0.75ftpk与0.65ftpk工况在0～11 ms 间二者位移时程曲线走势几乎一致，在11 ms 后，由于张拉控制应力为0.65ftpk时梁截面预压应力小于0.75ftpk，因此0.65ftpk时梁底中点O 竖向位移增加速率更快.0.55ftpk与0.45ftpk工况，二者位移数值不同，但位移时程曲线走势及外形轮廓极为相近.综上，实际工程中当考虑通过提升张拉控制应力提高预应力T 形梁抗爆性能时，要在适合的区间内选取张拉控制应力值.

由图12（b）可知：沿T 形梁底面纵向中轴线AA 上各点位移峰值分布基本规律为从中心处向两端逐渐减小.从图12（c）可见：沿T 形梁底面横向中轴线B-B 上各点位移峰值分布基本规律为从中心处向梁边缘处逐渐增大，产生这一现象的原因，是由于本文所研究的预应力T 形梁中有三根预应力钢绞线，其中预应力钢绞线N1 仅在二维平面内（即在x-O-y 坐标平面内）弯曲且水平段延伸长度较短，用来提供竖直向上部分的预应力数值较大，预应力利用率更高，而钢绞线N2 和N3 是在三维空间内弯曲的（即在x-O-y 坐标平面内弯曲的同时也在x-O-z 坐标平面内弯曲），但是N2 与N3 并不关于x-O-y 坐标平面对称，并且预应力钢绞线N2 和N3 的水平段延伸较长，用来提供竖直向上部分的预应力数值较小，二者预应力利用率与N1 相比较低.此外，随着张拉控制应力数值降低，T 形梁跨中底面横向中轴线B-B 上各点位移值整体有增大态势.

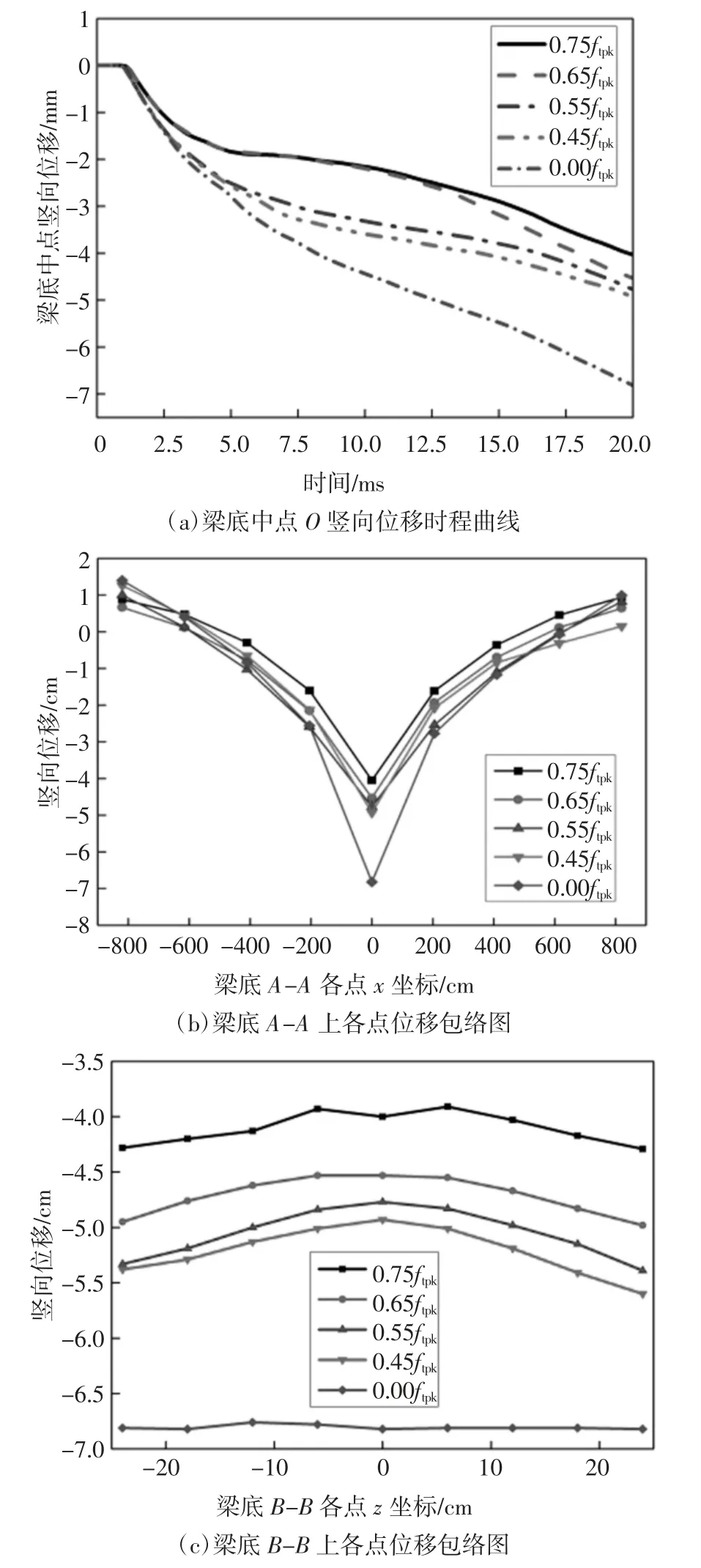
图12 5 种张拉控制应力下位移动态响应Fig.12 Dynamic response of displacement under five kinds of tensile control stress

4.2 纵向钢筋配筋率

为探究纵向钢筋配筋率对预应力T 形梁抗爆性能的影响，同时考虑到梁跨中部分处于炸药爆心正下方，所受冲击荷载最大，损伤最为严重，故选取T形梁跨中截面的纵向钢筋配筋率，并通过改变底层纵向钢筋ZJ-1（参见图1（b））的直径共分4 种纵向钢筋配筋率工况进行参数化分析，并保持张拉控制应力为0.75ftpk，混凝土强度不变为40 MPa，工况1：纵向钢筋配筋率0.004；工况2：纵向钢筋配筋率0.006；工况3：纵向钢筋配筋率0.008；工况4：纵向钢筋配筋率0.01.4 种工况下T 形梁底部中点O 竖向位移时程曲线对比图如图13（a）所示（位移方向以向下为负）.

图13（a）显示出4 种纵向钢筋配筋率下，T 形梁底部中点O 竖向位移时程曲线的变化趋势基本相同，随着纵向钢筋配筋率的提高，T 形梁底部中点竖向位移峰值逐渐减小，纵向钢筋配筋率为0.004 时，位移峰值为-4.55 cm；纵向钢筋配筋率为0.006 时，位移峰值为-4.05 cm，较纵向钢筋配筋率0.004 时减少10.99%；纵向钢筋配筋率为0.008 时，位移峰值为-3.75 cm，较纵向钢筋配筋率0.006 时减少7.41%；纵向钢筋配筋率为0.01 时，位移峰值为-3.42 cm，较纵向钢筋配筋率0.008 时减少8.8%.图13（b）和（c）显示出的沿T 形梁底面纵向中轴线A-A 和横向中轴线B-B 上各点位移峰值分布基本规律及产生该现象的原因均同4.1 节.因此，提高预应力T 形梁底层纵向钢筋的配筋率，对构件的抗爆性能有较好的增强效果，同时减小了T 形梁底部中点O 的位移峰值.

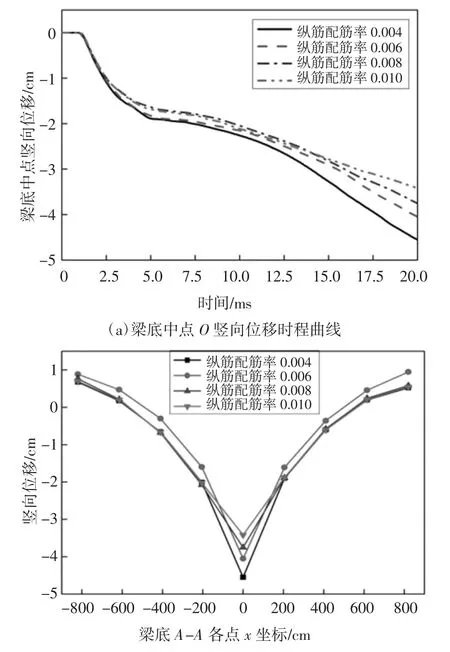
图13 4 种纵筋配筋率下位移动态响应Fig.13 Dynamic response of displacement under four longitudinal reinforcement ratios

4.3 箍筋面积配箍率

面积配箍率是决定预应力T 形梁抗剪承载力的重要因素之一，同时影响其抗爆性能.由于T 形梁两端加密区和中部非加密区的箍筋间距不同，故面积配箍率不同，考虑到本节采用改变箍筋直径的方式调整面积配箍率，因此选取跨中非加密区面积配箍率进行参数化分析，并保持张拉控制应力为0.75ftpk，混凝土强度为40 MPa，纵向钢筋配筋率不变为0.006.

图14（a）表示当T 形梁非加密区箍筋面积配箍率分别为0.004、0.006、0.008、0.01 时梁底中点O 竖向位移时程曲线对比图.20 ms 时4 种面积配箍率对应的位移值分别为-4.72 cm、-4.05 cm、-3.55 cm 和-3.51 cm.经分析可知：T 形梁底部中点O 的位移峰值随面积配箍率的增加呈现出非线性减少，面积配箍率为0.006 时，相对0.004 时减少14.19%，面积配箍率为0.008 时，相对0.006 时减少12.35%，面积配箍率为0.01 时，相对0.008 时减少1.13%，可见当面积配箍率从0.008 提高至0.01 时，T 形梁底部中点O的位移峰值减少并不明显.这是因为T 形梁的抗爆性能受多方面因素的影响（见4.1～4.3 节），而提高面积配箍率只从其中一方面增强梁的抗爆性能.当在0.004～0.008 范围内提高箍筋面积配箍率时，梁的抗爆性能改变明显，当超出这一范围时，梁的抗爆性能受其他因素的影响更为突出，因此工程实际中要依据具体工况选取面积配箍率.沿T 形梁底面纵向中轴线A-A 和横向中轴线B-B 上各点位移峰值分布如图14（b）和（c）所示.

图14 4 种箍筋配箍率下位移动态响应Fig.14 Dynamic response of displacements at four stirrup ratios

4.4 混凝土轴心抗压强度

混凝土作为预应力T 形梁的主要材料，兼具直接承受荷载及保护内部钢筋和钢绞线的重要作用，因此为研究冲击波-破片复合作用下混凝土强度对预应力T 形梁的损伤与动态响应的影响及其影响规律，本节共分以下5 种混凝土强度工况分别进行有限元数值模拟，其他数值模拟参数均保持不变，工况1：混凝土强度为30 MPa，工况2：混凝土强度为40 MPa，工况3：混凝土强度为50 MPa，工况4：混凝土强度为60 MPa，工况5：混凝土强度为70 MPa.5 种工况下T 形梁底部中点O 竖向位移时程曲线对比图如图15 所示（位移以向下为负）.

从图15 可知：混凝土强度为30 MPa 时，梁底部中点O 竖向位移峰值为-4.21 cm；40 MPa 时，位移峰值为-4.05 cm，较工况1 减少3.8%；50 MPa 时，位移峰值为-3.99 cm，较工况1 减少5.23%；60 MPa 时，位移峰值为-4.04 cm，较工况1 减少4.04%；70 MPa时，位移峰值为-3.84 cm，较工况1 减少8.79%，各工况位移峰值较为接近，最大差值为0.37 cm.此外5种工况下T 形梁底部中点O 竖向位移时程曲线的变化走势及形状非常相似，其中出现了60 MPa 时的位移值大于50 MPa 时的位移值，产生这一现象的原因是：借鉴文献[10]可知随着混凝土应变率增大，混凝土动态增强因子DIF 随之增大，而破片群对T 形梁的侵彻作用相当于小体积物体对混凝土的撞击问题，因此会出现由于混凝土较高应变率所带来的较大DIF 值使得综合作用下，出现以上5 种工况中混凝土动态强度基本接近的现象.综上，工程实际中要合理地选择混凝土轴心抗压强度，此外，由于混凝土应变率效应的存在，预应力T 形梁底部中点O 竖向位移峰值并不会随混凝土轴心抗压强度的增加而呈现线性增加.

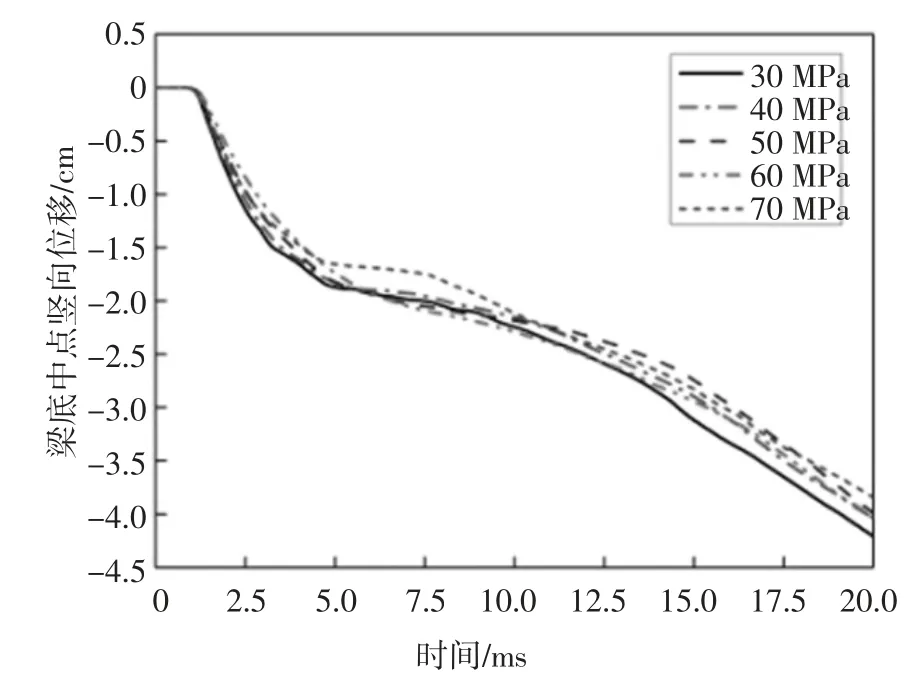
图15 5 种混凝土轴心抗压强度下梁底中点O 位移时程曲线Fig.15 Time-history curve of the midpoint O displacement of the bottom of the beam under the compressive strength of five kinds of concrete

5 炸药参数化分析

5.1 炸药比例距离相同

表4 数值模拟工况Tab.4 Numerical simulation conditions

图16 为预应力T 形梁在以上4 种工况下的塑性应变云图，经分析可知，冲击波-破片复合荷载对T 形梁的损伤作用体现为对上翼缘板的贯穿和对腹板的侵彻作用.随着ANFO 质量增大，虽然爆心与梁上表面的距离也在增加，但冲击波-破片复合荷载对梁上翼缘板的贯穿破坏范围在扩大.同时破片对腹板的侵彻深度在增加，爆心下方部分混凝土的应变值也在增加，高应变区域有扩大的趋势，其中当炸药质量为115.34 kg 时，炸药正下方腹板部分混凝土毁伤脱落十分严重，腹板内部纵向钢筋和箍筋裸露明显.同时，T 形梁跨中底部混凝土在高应力应变作用下失效严重，有明显剥落现象.

图16 炸药比例距离相同时塑性应变云图Fig.16 Cloud diagram of plastic strain at the same proportionof explosive

图17（a）为4 种工况下预应力T 形梁底部中点O 竖向位移时程曲线对比图，其中ANFO 质量为30.95 kg 时，位移峰值为-2.51 cm；质量为51.29 kg时，位移峰值为-3.75cm；质量为79.2 kg 时，位移峰值为-4.05 cm；质量为115.34 kg 时，位移峰值为-10.85 cm，其中工况4 相较于工况1 位移峰值增加332.27%，增幅巨大.由此得出结论：当保证炸药比例距离相同时，炸药质量的大小对预应力T 形梁的动态响应和毁伤效果的影响比炸药爆心到构件表面距离大小的影响更为突出.图17（b）及（c）所示的沿T形梁底面纵向中轴线A-A 和横向中轴线B-B 上各点位移峰值分布亦可反映以上结论.

图17 炸药比例距离相同时位移动态响应Fig.17 Dynamic response of displacement with the same proportion distance

5.2 爆心位置

当炸药爆心位于不同位置时，冲击波-破片的复合荷载对T 形梁的作用方式及破坏模式差异显著，因此，本节分别在T 形梁跨中翼缘板上方选取-1/2W W 为T 形梁上翼缘板宽度）、-1/4W、0、1/4W 和1/（W（即炸药爆心坐标z=-75 cm、z=-37.5 cm、z=0 c2m、z=37.5 cm 和z=75 cm）处共计5 种工况，对炸药爆心位置进行参数化分析，并保持其他各参数值均不变（5 种工况下爆心位置示意图如图18 所示），进一步研究当炸药爆心位于以上5 种工况中的位置时，T 形梁的位移动态响应及毁伤效果.对数值模拟数据结果进行整理，并作出T 形梁底面横向中轴线-B 上各点位移包络图，如图19 所示（位移方向以B向下为负）.

图18 5 种工况下爆心位置Fig.18 Schematic diagram of the position of the explosion center under five operating conditions

由图19 可见，当炸药爆心z 坐标值为-75 cm和-37.5 cm 时，T 形梁底面横向中轴线B-B 上各点位移峰值从靠近爆心一侧（爆心z 坐标为负值一侧）向远离爆心一侧（爆心z 坐标为正值一侧），近似呈均匀增加；当炸药爆心位于T 形梁面正上方（即爆心z 坐标为0 cm）时，T 形梁底面横向中轴线B-B 上各点位移峰值由底部中点O 向两侧近似逐渐增加；当炸药爆心z 坐标为37.5 cm 和75 cm 时，T 形梁底面横向中轴线B-B 上各点位移峰值从靠近爆心一侧（爆心z 坐标为正值一侧）向远离爆心一侧（爆心z坐标为负值一侧），同样近似呈均匀增加.此外，T 形梁底面横向中轴线B-B 上各点位移峰值整体均值，随着炸药爆心偏离中心点（即爆心z 坐标为0 cm 处）距离的减少而不断增加.出现以上现象的原因是：当炸药爆心偏离中心点（即爆心z 坐标为0 cm 处）位于梁面某一侧时，冲击波-破片的复合荷载主要作用在上翼缘板，而上翼缘板板面相对较薄，在破片群的撞击和冲击波超压复合作用下，靠近炸药爆心一侧的上翼缘板毁伤严重，翼缘板板面混凝土损伤失效发生剥落.爆炸后，上翼缘板被贯穿出较大尺寸的毁伤面，而远离炸药爆心一侧的翼缘板较为完好，冲击波超压会从靠近炸药爆心一侧的毁伤面透过T 形梁的上翼缘板，因此，冲击波超压对靠近炸药爆心一侧的上翼缘板作用力较弱，而对远离炸药爆心一侧的上翼缘板作用力较大，会在梁的横截面内形成扭矩使得T 形梁在20 ms 时，出现梁底面横向中轴线BB 上各点位移峰值从靠近爆心一侧向远离爆心一侧近似呈均匀增加的现象.同时，T 形梁底面横向中轴线B-B 上各点位移峰值整体均值，随着爆心偏离中心点距离的减少而不断增加.当爆心坐标z=-75 cm时，T 形梁的破坏及塑性应变云图见图20.