基于CR 全量非线性梁柱理论的平面剪切梁元

曾国良，颜东煌，陈常松†，董道福

（1.长沙理工大学 土木工程学院，湖南 长沙 410114；2.湖南联智科技股份有限公司，湖南 长沙 410019；3.江西省长大桥隧研究设计院有限公司，江西 南昌 330031）

结构分析经典理论认为：对于高跨比很小的细长梁，剪切变形与弯曲变形的比值较小，此时使用经典梁理论分析亦能得到满意的结果.但随着高跨比的增大，剪切变形在总变形中所占的比例将逐渐增大.当梁的高跨比较大（例如梁高h 与梁长l 关系满足h/l ＞1/5）时，剪切变形对梁总变形的影响不可忽略.为追求有限元分析的精度，需要在单元变形模式中考虑剪切变形效应.

在考虑剪切效应的梁元计算理论方面：Timoshenko 提出的两广义位移梁理论在初等梁（Euler-Bernoulli）理论的基础上取消直法线假定，将直梁理论推进至考虑剪切变形领域[1].随后深梁理论与有限元理论相结合，其中最简单的模式是文献[2]提出的线性插值单元，但其表征的单元具有曲率不变特性，且剪切刚度过硬，计算过程中还存在闭锁问题；文献[3]利用工程梁理论中的位移微分方程，将梁的弯曲变形与剪切变形分开考虑，导出了均匀梁的刚度矩阵；文献[4]则利用最小势能原理与横向位移三次插值函数（转角位移二次插值），消去内部自由度后得到深梁理论标准解答形式；文献[5]利用最小势能原理得到了考虑剪切变形的位移函数，并得到单元动力效应计算的相关刚度矩阵；文献[6]注意到Timoshenko 梁理论中挠度与转角的内在联系，提出了单广义位移深梁理论；文献[7]在两广义位移梁理论基础上，直接利用解析试函数建立深梁单元横向位移、转角及剪切应变的插值函数，进而导出了平面梁元动力计算刚度矩阵.上述方法基于增量分析理论，或者使用复杂的位移场函数，因此须以针对性方式提高其刚度矩阵精度方能得到更精确结果.

在考虑剪切效应几何非线性计算理论方面：基于空间框架结构计算理论的发展，文献[8]利用三维虚功增量方程结合三次位移插值函数（转角位移二次插值）分析了空间钢框架结构的几何非线性；文献[9]详细论述了考虑剪切变形影响的稳定插值函数的推导过程，并在随后的文献[10]中将其作为插值函数，基于UL 形状三维虚功增量方程，推导了考虑剪切变形影响的三维梁柱单元切线刚度矩阵并应用于空间钢框架的双重非线性分析，可以全面考虑弓弦效应、轴力与弯曲变形效应、剪切、扭转等空间耦合关系，并给出了算例，但文中未给出刚度矩阵的显式.文献[11]则借鉴初等梁的有限位移理论，利用Timoshenko 深梁的解析函数，分别更新了一般的基于稳定函数法的Saffan 理论、Brotton 理论、Fleming 理论.文献[12]推导了考虑剪切变形的拉-压杆刚度方程，其中的稳定函数包括了剪切变形对弯曲刚度的影响，并提出了采用幂级数展开式代替稳定函数的截断误差估计，文献[13-14]亦利用此项结论对空间框架进行了几何非线性验证，但该类文献皆未给出稳定函数展开式的简洁形状且未考虑剪切变形对梁柱理论“弓弦效应”的影响.此外由于空间薄壁结构的大量使用，其考虑剪切影响的相关理论亦大量发展，但其推导的刚度矩阵一般包含的维数较高[15-17].

基于弹性理论的几何非线性求解模式，经过多年发展已变得相对成熟[18-20]，尤其是基于增量方式求解当前时刻结构状态的方法更是被大多数软件采用.一般全量理论（节点力、非节点力全量及结构抗力全量）基于结构整体平衡条件，适用于多阶段、多工况结构连续施工有限元分析.关于结构抗力的全量计算，依据其利用的“刚度系数”的异同可分为基于切线刚度矩阵的全量算法[21-22]、基于割线刚度矩阵的全量算法[23].

事实上，很多非线性问题很难用有限元法的刚度矩阵和位移来精确表达内力[24]，因此在推导有限单元法时经常会碰触相关的近似问题，因此可寻求其他方式在单元级别进行求解：例如对悬链线索单元，则可通过柔性迭代[21]根据无应力长度及端点坐标得到单元内力；对于梁元则可在CR 坐标系下的单元级别上采用梁柱理论直接解析计算单元的全量抗力.

而在考虑剪切效应与实际超大跨度桥梁结构的几何非线性分析及现场实践方面，现有文献涉及较少，仅文献[24]针对主跨648 m 的南京长江三桥（主梁采用截面剪切形状系数μ 约为80 的薄腹宽翼缘钢箱梁）选取边跨落架、斜拉索第二次张拉及梁段起吊等三种典型工况，就施工控制过程中几何非线性和剪切变形的影响做了相应分析，并得到了一些具体的结论，但其有限元分析模式是基于增量型理论的.

基于上述求解梁元剪切效应理论及方法的特点，结合几何非线性增量求解理论现有成果，本文力求通过基于CR 法的全量（荷载无需分步施加）非线性求解方式，结合梁柱理论，得到全面精确考虑平面梁元轴力、弯曲、剪切及其耦合效应的简洁的高等梁元非线性分析快速求解方法.

1 考虑剪切效应的Timoshenko 梁理论

考虑如图1 所示笛卡儿坐标系中的弹性梁模型，其长度为L，宽度为b，高度为h.分析该问题时一般采用如下两类梁理论.

图1 梁坐标及尺寸示意图Fig.1 The figure of beam coordinates and dimensions

1.1 Euler-Bernoulli 梁理论

一般的Euler-Bernoulli 梁理论采用如下变形假定：

1）梁横截面在变形后仍保持平面，且始终垂直于中性轴，亦即直法线假定；

2）忽略转动惯量、剪切变形的影响；

3）不考虑轴向变形与横向（Z 向）变形的耦合作用.

基于以上假定的梁位移场可描述为：

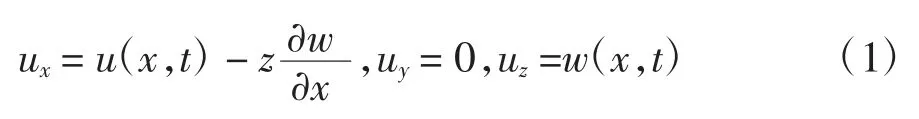
式中：x，y，z 表示单元内部各点位坐标值；ux，uy，uz表示沿三维坐标轴的线位移；w 表示单元各处的横向位移；t 表示时间度量.

对于细长杆件，一般将其横向剪切应变忽略，Euler-Bernoulli 梁理论可以给出足够精度的解.

1.2 Timoshenko 梁理论

相对Euler-Bernoulli 梁理论，Timoshenko 梁理论放松了横截面在变形后仍垂直于中性轴的假设，通过假定横向剪切变形为常量来计入横向剪切变形的影响，这种影响在短粗梁中显得十分重要[1].为了考虑简化的均匀剪切应变分布与实际剪切应变的差异，Timoshenko 引入了剪切修正系数[4]，此参数的确定受材料属性、截面几何参数及荷载与边界条件的影响.最终采用的梁位移场描述为：

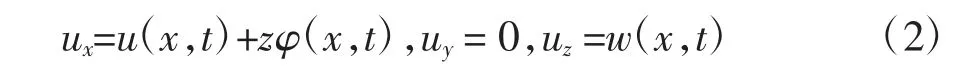
式中，φ 表示截面绕y 轴的转角.

由于本文不考虑结构动力特性，因而暂不考虑其他高阶梁理论，而是基于Timoshenko 梁理论，采用梁柱理论推导考虑剪切变形的稳定函数格式解，并提出相应的简洁且高精度拟合公式确保计算过程的稳定，使其最终适用于本文基于CR 法的全量计算理论.

2 基于CR 全量梁柱理论的几何非线性求解理论

如图2 所示，CR-TL 形式的全量求解方法中参考构形与现时构形分别约定为：以单元初始时刻（无应力）所处状态为参考构形，后续t 及t+Δt 时刻的计算皆以其为基准从而计算全量位移及内力，若需要对各时刻之间的增量求解，则利用不同时刻对应的全量结果进行累减即可得到.

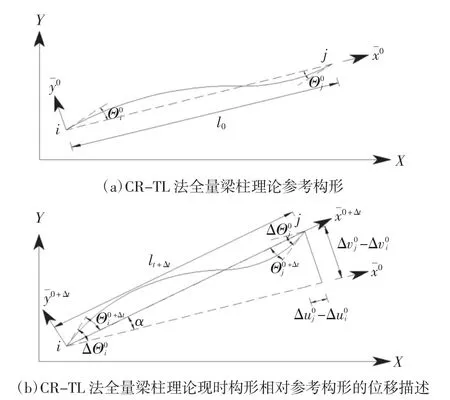
图2 CR-TL 全量梁柱理论坐标系统构成Fig.2 Co-ratational TL procedure system composition

如图3 所示，单元基于梁柱理论的CR 坐标[21]下的二阶平衡微分方程（小应变假设[25]）如下：

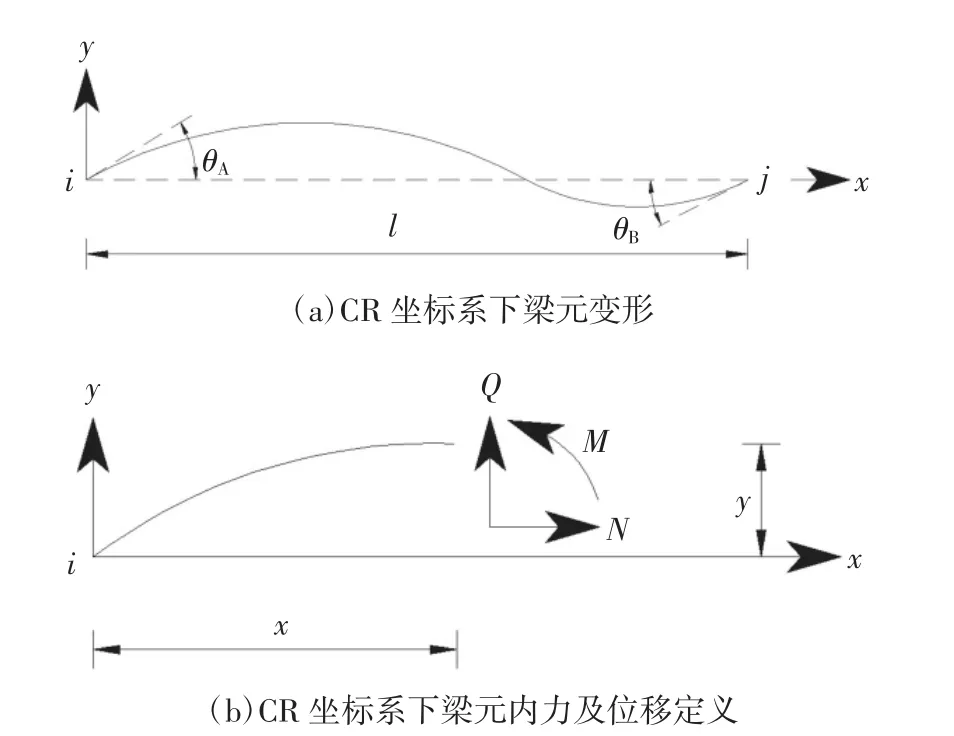
图3 基于CR 坐标的梁柱理论Fig.3 Beam-column theory based on Co-rotational procedure

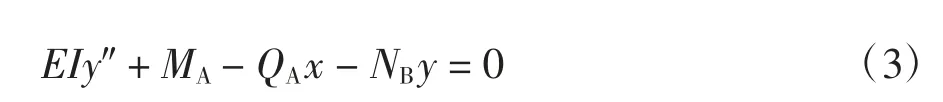
式中：EI 表示单元ij 的弯曲刚度；N、Q、M 则表示此单元的杆端抗力，其内力与位移符号皆按图中标注方向所示，并采用下角标A、B 对应单元ij 的杆端位置，另外采用i 表示单元弯曲线刚度.式（3）表示的梁柱刚度方程最终可用稳定函数表示为[26]：

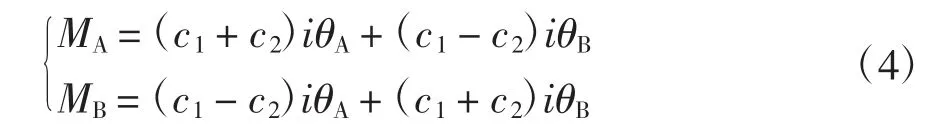
依据首末端的弯矩平衡方程可确定单元内的剪力；依据变形前后参数l0（单元无应力长度）、l（单元现时割线长度）并考虑“弓弦效应”可精确计算单元的轴力.文献[26]给出了不考虑剪切效应的具有明确截断准则的适用于-3.8≤NB/NE＜∞（NE为单元的欧拉临界荷载）范围的稳定函数幂级数解，本文亦采用相应思路并将其结果优化后为：

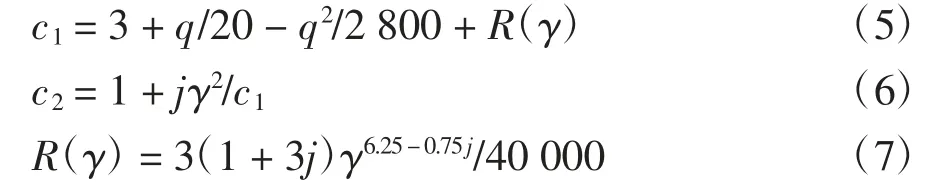
式中：j 为依据轴力NB确定的符号函数，当NB＞0 时取j=1，否则取j=-1，同时

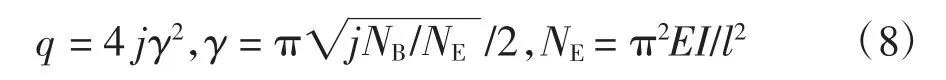
考虑梁柱构件的“弓弦效应”，则对单元的轴力修正量为[27]：

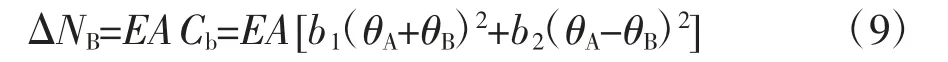
其中：

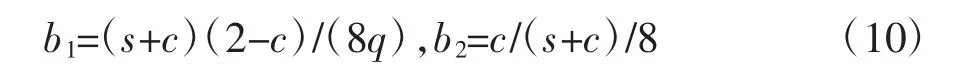
上述式中的系数s、c 均与单元的轴力相关，且有转换关系：

当轴力很小时（可设定为γ≤1.2e-3），对相关公式考虑截断误差影响后，可简化为：

上述基于梁柱理论的考虑梁元轴力、弯矩及其耦合效应的杆端抗力计算公式可由梁元“无应力状态”时刻作为起始计算时间节点，利用梁元CR 坐标下的杆端累计位移直接解析计算当前时刻的单元全量抗力，明显区别于增量理论常见的抗力逐步叠加方式，可实现无需多个荷载步约束条件下的非线性有限元精细计算，提高结构分析效率[28].

3 考虑剪切效应的平面二阶转角位移方程

Timoshenko 梁理论仍保留初等梁理论中的平截面假定，但放弃了直法线假定，从而克服了初等梁理论平衡方程中剪切应力（全截面内表现为剪力）不为零而剪应变为零的矛盾，使得剪切方向的本构关系在平均意义上（假定剪切应变沿横截面均匀分布，实际上剪切应力沿横截面的非均匀分布通过此剪切系数μ 考虑）得到满足.

仍采用图3 所示坐标系建立平衡方程.考虑剪切变形效应时，梁的法向位移（挠度）表示为两部分的叠加[14]，即：

式中：yb是由梁的弯曲变形引起的法向位移；ys是由梁的剪切变形引起的法向位移.

利用单元截面的弯矩平衡条件及小应变下的弯曲变形曲率计算公式，将式（3）改写，得到：

利用文献[25]同样方式可建立剪切变形引起的法向位移ys与总位移y 二次微分之间的相互关系.

经推导，上式最终亦可用结构类似前述式（4）所示的稳定函数.并依据首末端的弯矩平衡方程可确定单元内的剪力；依据变形前后参数l0、l 并考虑“弓弦效应”可精确计算单元的轴力.经详细演算，本文给出考虑剪切效应的具有明确截断准则的适用于NB/NE∈[-2.5，2.5]（NE为单元的欧拉临界荷载）范围的稳定函数幂级数解：

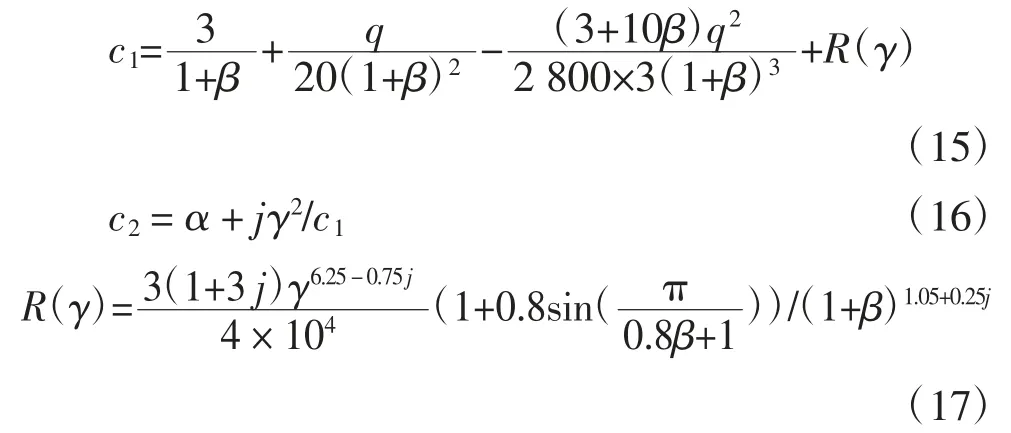
式中：当NB＞0 时取j=1，否则取j=-1；当γ≤0.1时，取R（γ）=0；另有系数β 定义为：

上式中，μ 表示截面剪切系数，G，A 分别表示材料剪切模量及单元横截面面积.此外：

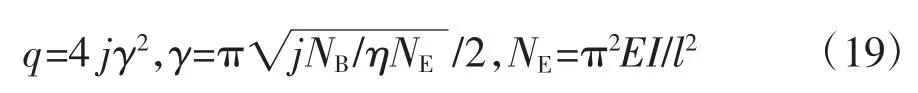
上式中参数η 表示为：

同理，考虑梁柱构件的“弓弦效应”后对单元的轴力修正量为：

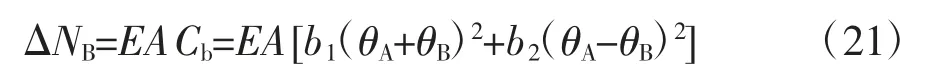
上式中参数u 计算方式为：

上述系列式中的系数s、c 同样均与单元的轴力相关，且有式（11）的转换关系.

当轴力很小时（经验证可设定为γ≤1.2e-3），有：

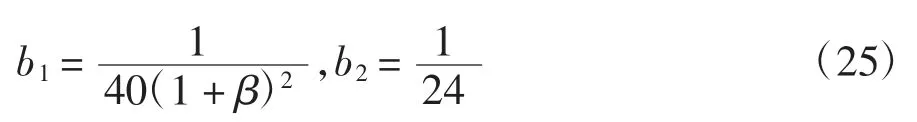
从上述求解平面剪切梁元问题过程可以看出：基于梁柱理论（稳定函数格式）解析方式可以逐单元直接求解梁元全量杆端抗力而无需进行力的叠加计算.实际上从后续验证实例还可发现，运用此类方法求解非线性问题时，无需求解得到复杂形状的切线刚度矩阵.形状复杂的各类刚度矩阵不仅求解过程繁琐，求解效率偏低，而且对最终的求解结果无改善效果.因此，本文确定的方法在求解该类问题时具有一定的特点及优势.

4 算例考证

为验证本文理论的正确性，同时验算其计算流程的可靠性，使用如下算例进行对比分析计算，并取其中部分结果与以往经典文献资料进行对比.

4.1 受集中弯矩作用的悬臂梁

如图4 所示，为验证本文CR 全量梁柱理论的正确性及快速求解效率，利用被诸多文献引用来验证程序大转动功能和数值方法的经典固端悬臂梁算例，将水平悬臂梁等分成20 个单元，其自由端作用一集中力偶M=K（2πEI/L）.表1 是本文采用不同方式的计算结果（Np表示荷载步数量）.

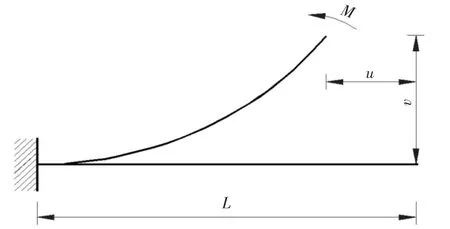
图4 受集中力偶作用的固端悬臂梁Fig.4 A fixed-end cantilever beam under the action of a concentrated couple

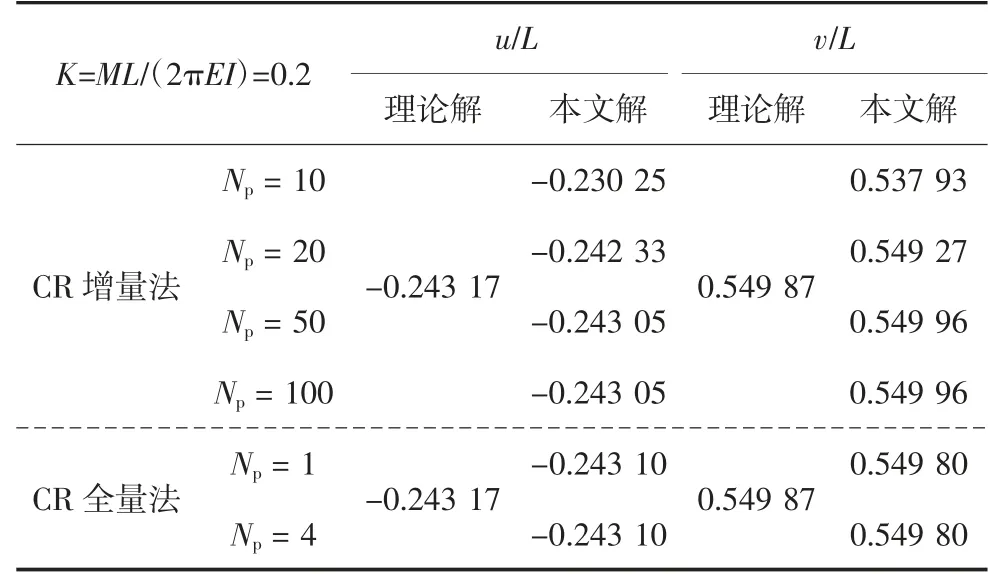
表1 受集中弯矩作用的悬臂梁自由端位移比较Tab.1 Comparison of the displacement of the free end of the cantilever beam under the action of concentrated bending moment

从表1 列出的对比结果可以看出：1）本文CR全量方法求解大位移问题时仅需要一个荷载步即可得到足够精确的结果.2）CR 增量方法在荷载步设定为足够大值时，其计算结果仍存在一定误差；而CR全量方法增大荷载步对计算结果无影响，这是因为CR 全量方法基于最终的平衡状态直接求解全量平衡方程，且精确考虑了梁元的“弓弦效应”影响.

4.2 三跨连续梁受集中荷载作用

如图5 所示的等截面单箱单室箱形三跨连续梁，其跨中作用一集中力P=2 000 kN，材料弹性模量E=37 000 MPa，泊松比λ=0.16，截面剪切系数μ=1/0.328 749.

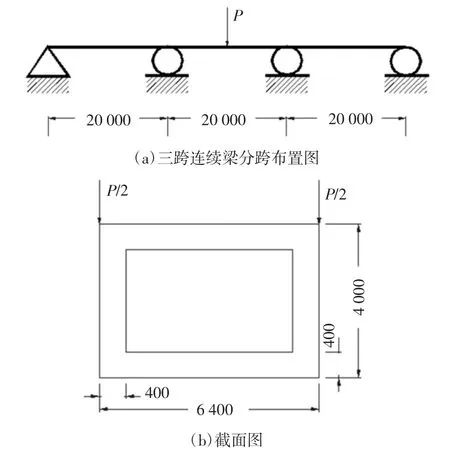
图5 三跨连续梁分跨布置及截面图（单位：mm）Fig.5 The figure of layout and cross section of three span continuous beam（unit：mm）

最终的计算及对比结果见表2.从表2 的对比结果可以看出，本文计算结果与参考文献计算结果一致，说明本文计算方法可靠.

4.3 Williams 刚架受集中力作用

如图6 所示的Williams 双杆体系（Williams Toggle Frame）.体系高度h=9.8 mm（0.386 in），半跨宽为l=328.75 mm；材料及截面属性为：弹性模量E=71 018.5 MPa，泊松比取λ=0.28，截面剪切不均匀系数取μ=1.2，截面尺寸为：19.13 mm×6.17 mm，面积A=118.05 mm2，截面绕弱轴弯曲，I=374.77 mm4.分析时每个杆件仍取5 个梁单元模拟，计算结果如图7 所示.

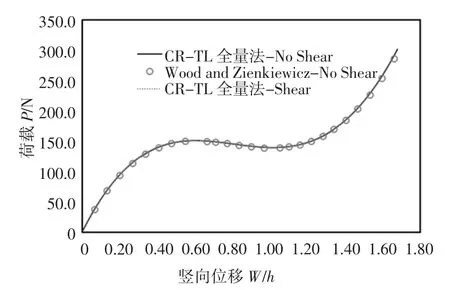
图7 Williams 刚架体系荷载-位移曲线（考虑剪切效应）Fig 7 Load-displacement curve of Williams frame system（considering shear effect）

从图7 显示的对比结果可以看出，采用本文考虑剪切效应的CR 全量理论结合GSP 法[12]处理非线性求解过程中路径跳跃问题，可以分析肘型刚架荷载-位移全过程变形特征，且精度较高.此外，本文跃越屈曲第一及第二临界点对应的荷载值分别为Pcr1=150.599 3 N，Pcr2=139.190 0 N；按本文考虑剪切效应时其相应临界荷载值为Pscr1=150.5002 N，Pscr2=139.034 2 N，本文计算结果与文献[14]计算结果非常接近.

4.4 特大跨度斜拉桥施工过程主梁剪切效应计算

采用某主跨818 m 钢箱梁斜拉桥及某主跨720 m 钢桁梁斜拉桥工程作为对比分析对象，在考虑与不考虑剪切效应条件下，选取其悬臂施工过程中部分计算结果，论证本文计算分析理论.其中钢箱及钢桁梁主梁斜拉桥部分构件的截面剪切形状系数μ 值对比分别如表3 及表4 所示.

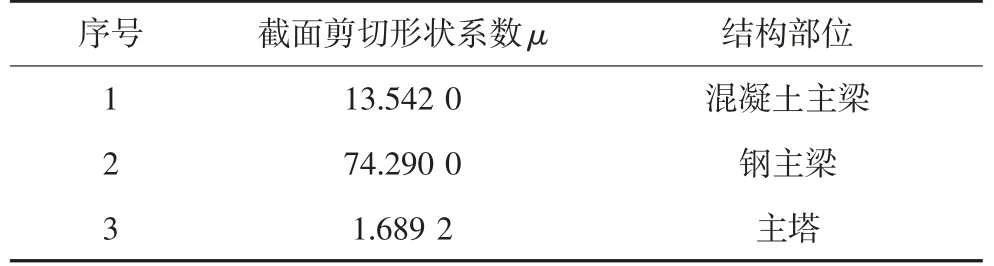
表3 钢箱主梁斜拉桥部分构件截面剪切形状系数μ 值对比Tab.3 Comparison of cross section shear shape coefficient μ value of some part of steel box girder cable-stayed bridge

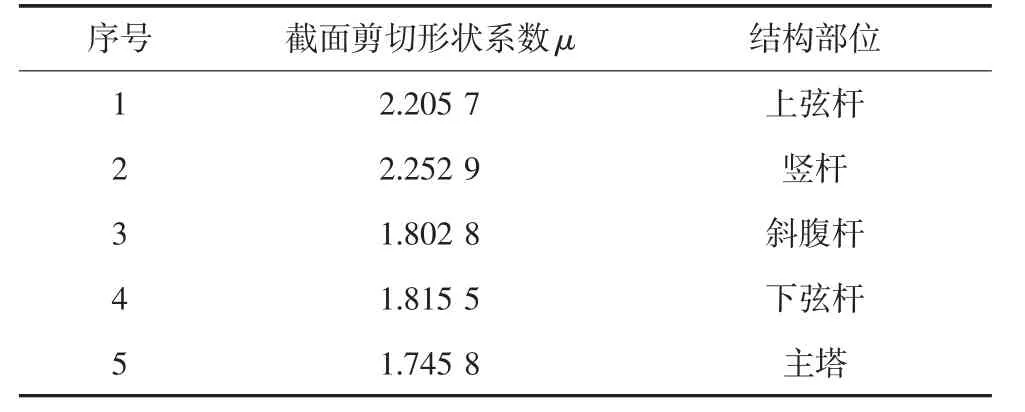
表4 钢桁主梁斜拉桥部分构件截面剪切形状系数μ 值对比Tab.4 Comparison of cross section shear shape coefficient μ value of some part of steel truss girder cable-stayed bridge

从上述两工程背景中结构代表性构件截面剪切形状系数对比可知：主塔构件由于几何尺寸布置相似，因此截面对应系数相近；混凝土尤其是钢箱主梁较桁式主梁截面剪切形状系数明显偏大.

假定上述两工程背景中主梁采用悬臂拼装法施工，限于本文篇幅，现分别选取第五号、十五号、二十五号梁段关键施工工况，采用以下两种计算模式进行分析对比.

Ⅰ：完全非线性且不考虑剪切效应；Ⅱ：完全非线性且考虑剪切效应.

选取中跨钢箱/桁主梁施工过程主梁悬臂端阶段位移进行对比，其结果如表5 所示.

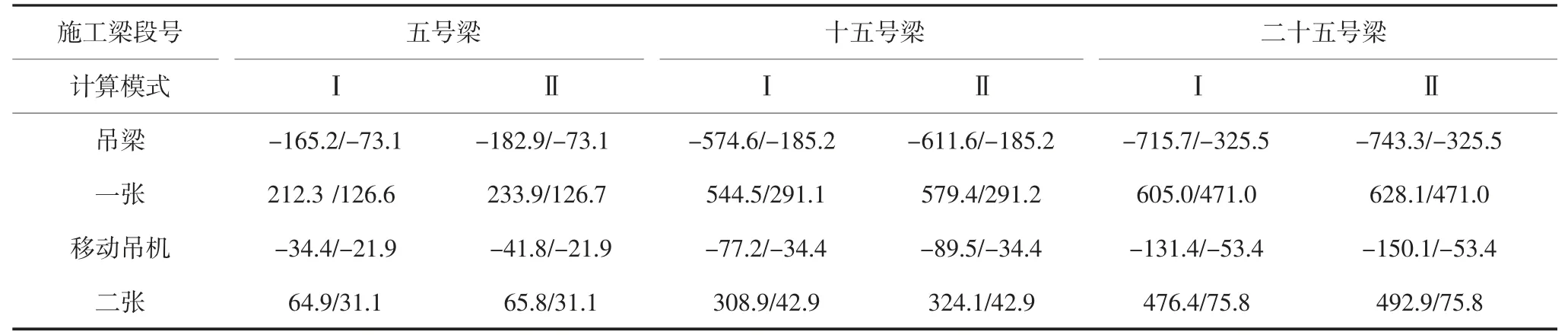
表5 中跨钢箱/桁主梁施工过程主梁悬臂端阶段位移对比Tab.5 Comparison of cantilever girder end displacement during construction of medium span steel box/truss main girder mm

从上述阶段位移对比系列表中可以看出：①钢箱式主梁是否考虑剪切效应对主梁阶段位移的影响较大，钢桁式主梁是否考虑剪切效应对主梁阶段位移的影响微小；②梁段施工过程中在弯矩变化较大工况皆存在一定量的剪切效应，若不考虑剪切效应，则相对间接提高了主梁的竖向刚度；③是否考虑剪切效应对钢箱主梁阶段位移的最大影响量为40 mm级别；④随着主梁悬臂长度的增加，剪切效应引起的位移比例值逐渐减小，悬臂根部附近处该值达到10%左右（剪切位移绝对值约20 mm）.

因此，是否考虑主梁剪切效应将显著影响施工过程中几何线形评估；同时根据本算例中基于非线性增量及全量理论计算时间对比结果看，相同条件下，利用本文全量理论可节约30%计算机时，加快分析进度.

5 结论

根据本文基于CR 全量非线性计算模式，利用梁柱理论建立的考虑梁元轴力、弯矩、剪力及其耦合效应的梁元分析理论及其验证结果，可得：

1）基于CR 列式法，考虑剪切变形效应的基于梁柱理论全量求解的稳定函数格式及采用简化的幂级数考虑梁元“弓弦效应”理论，可作为同类非线性计算理论的重要补充.

2）通过与经典算例结果的对比分析，验证了本文推导的考虑剪切变形效应的梁元及其求解过程的实用性及精确性，计算结果与相关文献吻合良好，说明本文方法可靠，可作为考虑剪切变形效应几何非线性有限元分析的基本方法.

3）通过两个不同类型超大跨度斜拉桥实际工程对比验证，本文计算理论可在保持计算精度的基础上节约大量计算机时.

4）本文暂未建立基于梁柱理论且考虑各因素耦合效应的三维空间梁元高精度分析理论，下一步可从理论分析方面进行再分析，从而建立少单元、少荷载步但高精度的空间梁元几何非线性快速精细求解理论.