一类具有标准发生率和双垂直传播的媒介传染病模型分析
2021-07-23刘晨窦霁虹李玉峰赵婷婷
刘晨, 窦霁虹, 李玉峰, 赵婷婷
(西北大学数学学院, 陕西 西安 710127)
1 引言
媒介传染病是通过一种被称为生物媒介载体传播的传染性疾病, 通常由病毒、细菌、原生动物或立克次体等引起的, 特别是蚊媒疾病, 例如疟疾、登革热、西尼罗河热等[1], 给人们的生活带来巨大的影响, 时刻威胁着人们的生命健康. 随着科学技术的迅速发展, 医学界不断尝试去解决长久以来困扰人们的疾病问题. 然而, 理论是实践的基础, 大量的传染病动力学模型推动着对传染病问题的研究. 人们更多地关注决定疾病爆发后是持续流行还是逐渐消亡的阈值, 即基本再生数[2], 从而能更好地控制疾病的传播.
根据文献[3-4] 可知染病媒介的繁殖后代中有部分携带病毒, 能够进行疾病的传播;在2014 年关于新生儿登革热的报告中, 表明新生儿的病因正是由于母婴垂直传播[5].因此, 在实际的病例中确实存在人群和媒介均具有垂直传播这种双垂直传播传染病的传播机制, 但现今对双方同时考虑垂直传播特征的疾病研究还为数不多.
因此, 本文建立了一类具有标准发生率和双垂直传播的媒介传染病模型, 并对其动力学形态进行理论分析证明与数值模拟, 进一步完善对媒介传染病模型的研究.
2 模型建立
假设在传染病流行期间, 该地区人群的迁移忽略不计, 同时不考虑因病死亡, 且人群的出生率和死亡率相等用µH表示, 则总人群维持于一个固定的常数N.SH(t),IH(t) 及RH(t) 分别表示易感者, 带病毒人群(简称患者) 及康复者在t时刻相应的数量. 对于媒介(如蚊子) 而言, 繁殖周期短, 产量大, 每日的出生量和死亡量都十分巨大,在无人为干扰的情况下, 媒介总数的变化量相对于该种群总数可忽略不计, 因此假设媒介总数也维持于一个固定常数M, 媒介的出生率和死亡率均为µM.SM(t),IM(t) 分别表示易感媒介和染病媒介在t时刻相应的数量.
根据媒介习性的不同, 将易感媒介每日接触人的频率记为a1, 染病媒介每日接触人的频率相对更高记为a2, 同时感染效率也有所不同[6-7], 将易感媒介接触一次患者获病的概率记为b1, 易感者接触一次染病媒介病的概率相对更高记为b2, 疾病的发生率均为标准发生率.r表示患者的康复率, 患者一旦康复可对该疾病终身免疫, 人群和媒介各自的垂直传染率分别为qH及qM. 可得此类媒介传染病传播的流程图如图1.
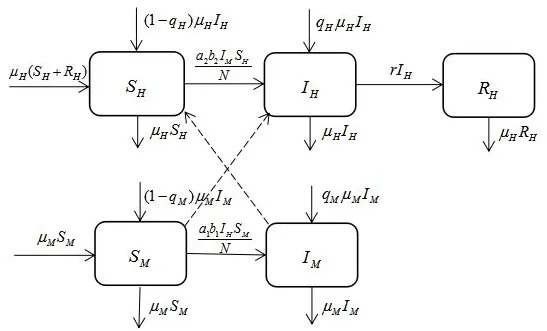
图1 媒介传染病的传播流程图
根据建模思想, 本文建立如下动力学模型:
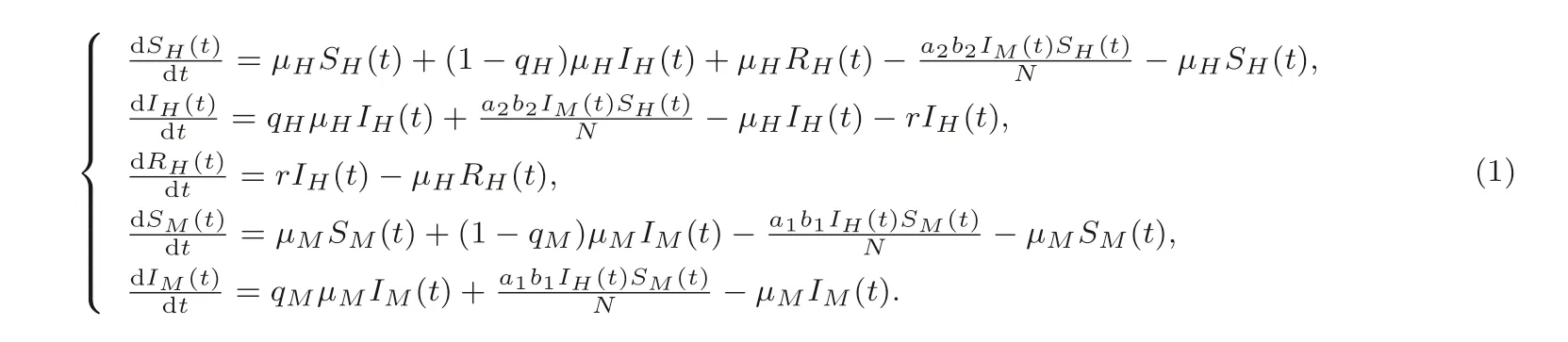
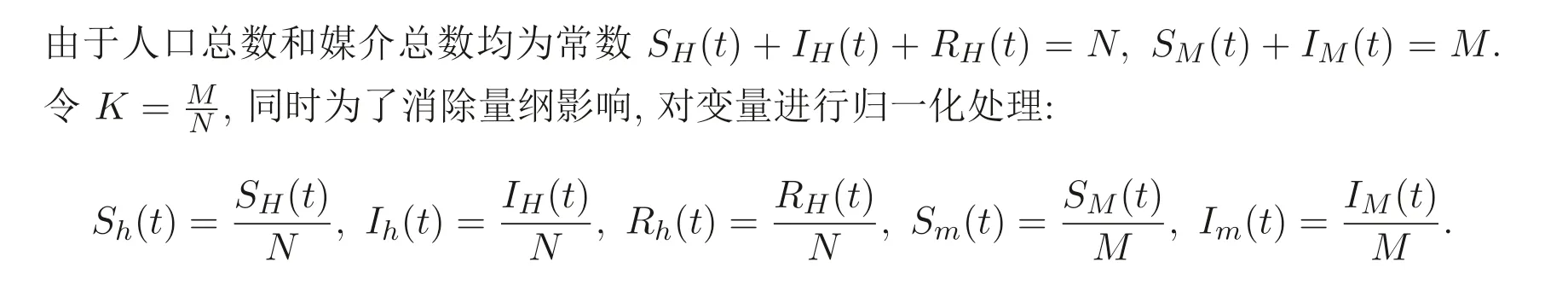
根据Rh(t) = 1−Sh(t)−Ih(t), Sm(t) = 1−Im(t), 对模型(1) 进行降维, 因此只需考虑如下系统:
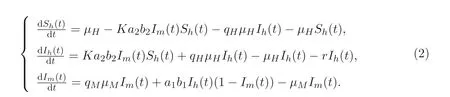
考虑到实际背景, 模型的解均为非负数, 本文仅在可行域Ω 中进行讨论,

3 基本再生数的计算
令模型(2) 右边各等式等于0, 易得该模型的无病平衡点E0(1,0,0). 本文采用Driessche 和Watmough 的第二代生成矩阵法[8], 给出基本再生数的表示.
令X=(Ih,Im,Sm)T,β1=a1b1,β2=a2b2, 则模型(2) 可等价为

其中,
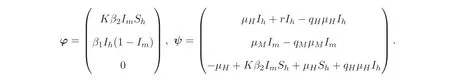
φ,ψ在无病平衡点E0处的雅克比矩阵分别如下:
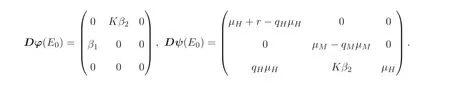

当基本再生数R0<1 时, 意味着平均每位患者在其患病期内导致新增患病人数不足一人, 疾病逐渐消亡; 反之, 当基本再生数R0>1 时, 意味着疾病持续蔓延.
4 平衡点的存在性
定理4.1若R0<1, 模型(2) 只存在无病平衡点E0(1,0,0); 若R0>1, 模型(2)存在唯一的地方病平衡点E∗(S∗h,I∗h,I∗m).
证明令模型(2) 右边各等式等于0, 计算得

当R0<1 时,Ih=0, 模型(2) 只存在无病平衡点E0.
5 平衡点的稳定性
定理5.1当R0< 1, 模型(2) 的无病平衡点E0(1,0,0) 是局部渐近稳定的;当R0>1 时, 则不稳定.
证明模型(2) 在无病平衡点E0(1,0,0) 处的雅克比矩阵为

对应的特征方程为

解得λ1=−µH<0.另外两个特征根由下面的方程决定

整理得

其中,c1=µM(1−qM)+µH(1−qH)+r, c2=(1−R20)µM(1−qM)[µH(1−qH)+r].
由c1> 0, 且当R0< 1 时,c2> 0, 根据Hurwitz 判据可知, 方程(7) 所有特征根均具有负实部. 因此, 无病平衡点E0是局部渐近稳定的; 当R0> 1 时,c2< 0, 则方程(9) 有一正根, 故无病平衡点E0不稳定.
定理5.2当R0<1, 模型(2) 的无病平衡点E0(1,0,0) 是全局渐近稳定.
证明构造正定的Lyapunov 函数
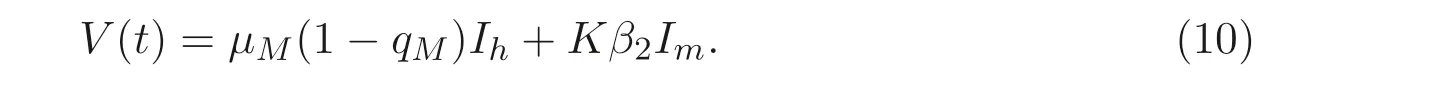
其沿模型(2) 轨线的导数为
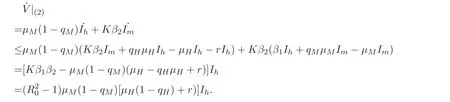
当R0<1 时, ˙V ≤0, 当且仅当Ih=0 时, ˙V=0. 此时Sh=1,Im=0, 故无病平衡点为唯一的不动点,{E0}是{Sh,Ih,Im ∈Ω : ˙V= 0}的最大不变集. 由LaSalle 不变集原理[9]可得, 当R0<1 时, 模型(2) 的无病平衡点E0是全局渐近稳定的.
定理5.3在R0>1 的基础上,当满足条件(H1)R20[µH(1−I∗m)−(µH+r)I∗h)]<µH时, 模型(2) 的地方病平衡点E∗(S∗h,I∗h,I∗m) 是局部渐近稳定的.
证明当R0>1 时, 模型(2) 在地方病平衡点E∗处的雅克比矩阵经矩阵变换为
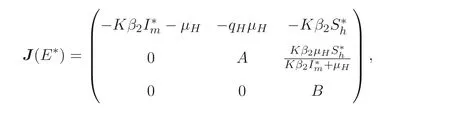
其中

经整理

由条件(H1), 得
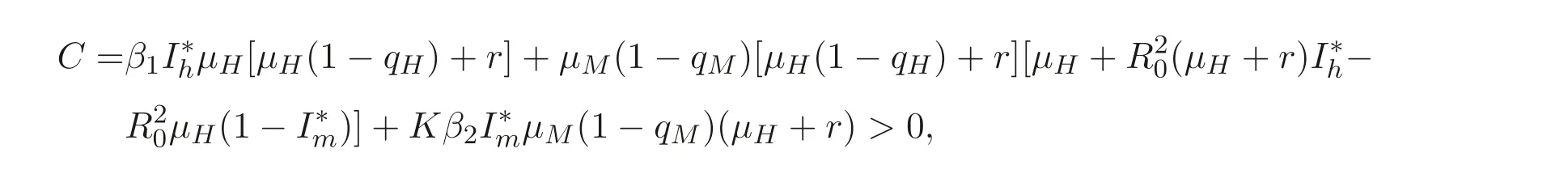
则B<0. 因此, 地方病平衡点E∗(S∗h,I∗h,I∗m) 是局部渐近稳定的.
定理5.4在R0> 1 的基础上, 当满足条件(H2)µH+r −2qHµH> 0 时, 模型(2) 的地方病平衡点E∗(S∗h,I∗h,I∗m) 是全局渐近稳定的.
证明根据文献[10] 及定理5.2 知, 当R0>1 时,E0不稳定, 则在Ω 内存在一个紧吸引子集Γ, 且模型(2) 存在唯一的地方病平衡点E∗, 故满足文献[11] 中定理3.3.7的条件, 下面证明q<0.
模型(2) 的雅克比矩阵的第二加性复合矩阵为
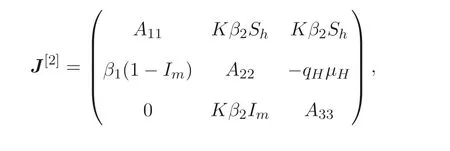
其中,

其中,

令(u,v,l)∈R3, 其范数‖·‖定义为‖(u,v,l)‖= max{|u|,|v|+|l|}, 相应于范数‖·‖的Lozinskiˇi 测度是µ(B),µ(B)≤sup{g1,g2}, 其中

将B22的每一列非对角元素取绝对值后加到相应列的对角元素上, 取其两个对角元素的最大值, 则

由条件(H2) 知,η=min{µH,µH+r −2qHµH}>0. 利用

则对所有满足初值的X0=(Sh(0),Ih(0),Im(0))∈Γ, 当t>t∗时, 有

又由Ω⊆R3是单连通, 故根据文献[11] 中的定理3.3.7 证毕.
6 数值模拟
为了对以上理论结果进行验证, 本文参考文献[6] 对参数进行适当地选取, 借助Matlab 软件进行数值模拟, 针对不同的基本再生数计算结果, 描绘出疾病的发展趋势.
(1) 选取参数K= 10,a1= 0.12,a2= 0.28,b1= 0.5,b2= 0.8,qH= 0.3,qM= 0.36,µH= 0.2,µM= 0.6,r= 0.25. 此时计算得R0= 0.9473< 1. 图2 为易感者比例Sh(t)、患者比例I(t) 及染病媒介比例Im(t) 随时间t的变化情况.
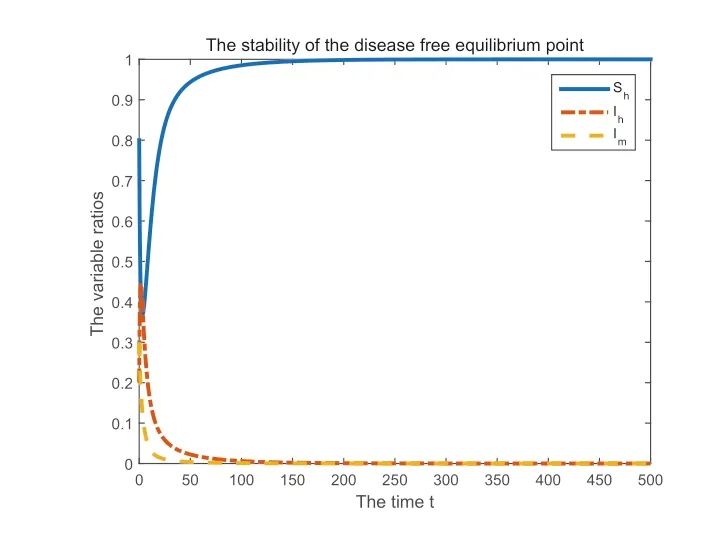
图2 无病平衡点的稳定性(R0 =0.9473)
(2)选取参数K=10,a1=0.12,a2=0.2,b1=0.5,b2=0.8,qH=0.3,qM=0.36,µH=0.2,µM=0.6,r=0.4. 此时计算得R0=0.6211<1. 图3 为易感者比例Sh(t)、患者比例I(t) 及染病媒介比例Im(t) 随时间t的变化情况.

图3 无病平衡点的稳定性(R0 =0.6211)
通过图2 和图3 可以直观地看出, 当R0<1 时, 易感者比例逐渐趋于1, 患者比例和染病媒介比例逐渐趋于0, 无病平衡点在可行域内是全局渐近稳定的. 另外, 通过比较两图, 可以发现当减小人群与媒介之间的接触率、增大疾病的康复率, 会引起基本再生数减小, 从而导致疾病更快的走向消亡.
(3) 选取参数K= 10,a1= 0.25,a2= 0.37,b1= 0.5,b2= 0.8,qH= 0.3,qM= 0.36,µH= 0.2,µM= 0.6,r= 0.08. 此时计算得R0= 2.0928> 1. 图4 为易感者比例Sh(t)、患者比例I(t) 及染病媒介比例Im(t) 随时间t的变化情况.
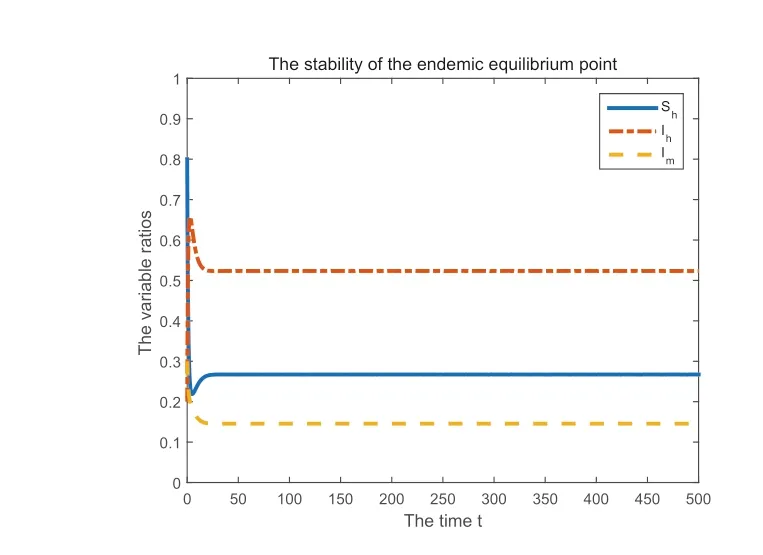
图4 地方病平衡点的稳定性(R0 =2.0928)
(4) 选取参数K= 10,a1= 0.12,a2= 0.28,b1= 0.5,b2= 0.8,qH= 0.3,qM=0.36,µH=0.2,µM=0.6,r=0.1. 此时计算得R0=1.2076>1. 图5 为易感者比例Sh(t)、患者比例I(t) 及染病媒介比例Im(t) 随时间t的变化情况.

图5 地方病平衡点的稳定性(R0 =1.2076)
通过图4 和图5 可以直观地看出, 当R0>1 时, 随着时间的推移, 易感者比例、患者比例和染病媒介的比例均趋于各自的一个稳定值, 可见地方病平衡点在可行域内是全局渐近稳定的. 另外, 通过比较两图, 可以发现若减小人群与媒介之间的接触率、增大疾病的康复率, 从而引起基本再生数减小, 则会导致当疾病发展到地方病平衡点时, 相应的患者比例会稳定在更小的数值.
进一步根据基本再生数的表达式
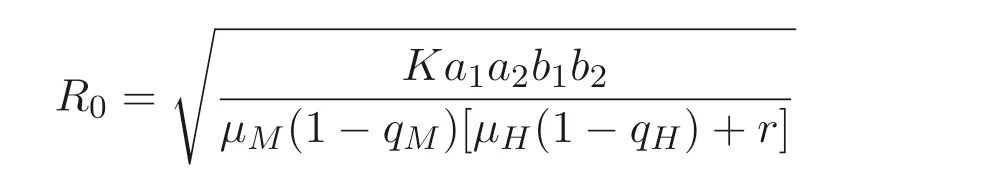
可知,R0与人群的垂直传染率qH及媒介的垂直传染率qM正相关. 因此, 相比宿主和媒介中一方具有垂直传播, 或双方均不考虑垂直传播的情况而言, 当加入双垂直传播特征时, 会引起基本再生数增大, 从而R0<1 时, 疾病消亡的时间会相对延长;R0>1 时,疾病到达地方病平衡点相应的患者比例有所提高.
7 结论
本文考虑到在媒介传染病中存在传播媒介和宿主均具有母婴垂直传播的实际情况,建立了一类具有标准发生率和双垂直传播的媒介传染病模型, 并对模型进行了定性分析和定量模拟, 从而达到了对媒介传染病进一步完善研究的目的. 最后, 通过计算机不仅实现了对模型的数值模拟, 验证了理论结果的有效性, 而且通过比较不同基本再生数下的疾病发展趋势, 直观地说明了采取减小人群与媒介之间接触率的相应措施, 或者采取有效的治疗方法提高康复率, 能够使得基本再生数降低, 从而可以达到控制疾病蔓延的效果, 此为实际应用提供了理论依据. 另一方面, 说明了相对于不考虑双垂直传播因素,增加该因素之后, 会引起基本再生数的增大, 从而导致疾病消亡的时间延长, 地方病平衡点对应的患者比例提高.
