含非线性项的不确定离散时滞系统鲁棒稳定性分析

孙延修, 潘斌

(1. 沈阳工学院基础课部, 辽宁 抚顺 113122; 2. 辽宁石油化工大学理学院, 辽宁 抚顺 113001)

1 引言

离散时滞系统的鲁棒稳定性问题已经取得了丰富的研究成果, 在实际控制问题中由于系统建模误差及工作环境的变化, 系统往往存在不确定性[1-2]. 针对系统的稳定性,鲁棒控制可以保证闭环系统具有一定的鲁棒性能, 受到了很多学者的关注并取得了一定的成果.

在实际控制系统中, 考虑系统状态的时滞性、参数的不确定性及系统的非线性扰动等因素具有较强的实际意义[3-4]. 文献[5] 针对范数有界的一类不确定离散时滞系统给出了鲁棒稳定性判定标准, 并设计出了基于状态反馈的鲁棒控制器, 文献[6] 针对非线性时滞系统, 利用线性矩阵不等式方法将最优化求解困难的问题转化成具有LMI 约束的凸优化问题, 并给出鲁棒预测控制器存在的充分条件及其表达式, 文献[7] 针对一类非线性离散时滞广义系统的观测器进行了研究, 并给出了观测器存在的充分条件, 从而使状态误差系统渐近稳定.

本文在基于文献[5] 的基础上考虑到系统的非线性扰动, 通过利用线性矩阵不等式方法对系统的鲁棒稳定性进行分析, 以LMI 形式给出了系统渐近稳定的充分条件, 并设计出状态反馈控制器使得系统渐近稳定.

2 系统描述

考虑如下不确定时滞系统

其中,x(k)∈Rn为系统状态向量,A ∈Rn×n,Ad ∈Rn×n, 为适当维数的常数矩阵,ΔA,ΔAd为参数不确定项, 满足如下条件:

其中,D,E,Ed为已知适当维数的常数矩阵,F(k) 为未知时变函数矩阵, 满足

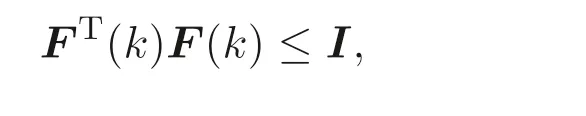
令非线性项

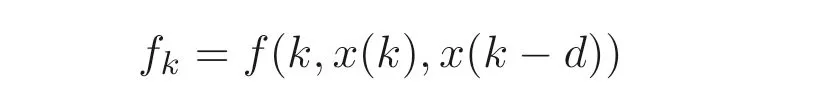
且满足

引理2.1[8]给定适当维数矩阵M,N和对称矩阵G, 对满足FT(k)F(k)≤I的矩阵F(k), 不等式G+MF N+NTFTMT< 0 成立的充要条件是存在实数ε> 0,使得

3 系统稳定性分析

考虑系统(1) 中非线性函数项所满足的约束条件, 利用线性矩阵不等式(LMI) 的方法, 可以得到不确定时滞系统渐近稳定的充分条件.

定理3.1若存在对称正定矩阵P,Q满足下列不等式

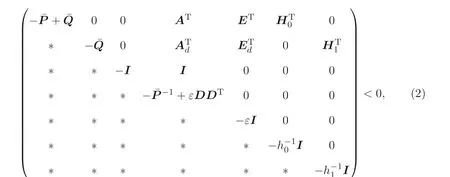
其中,P>0, Q>0, 证明V(x(k)) 沿系统(1) 的差分为负, 即

可以保证系统渐近稳定.

由于

即

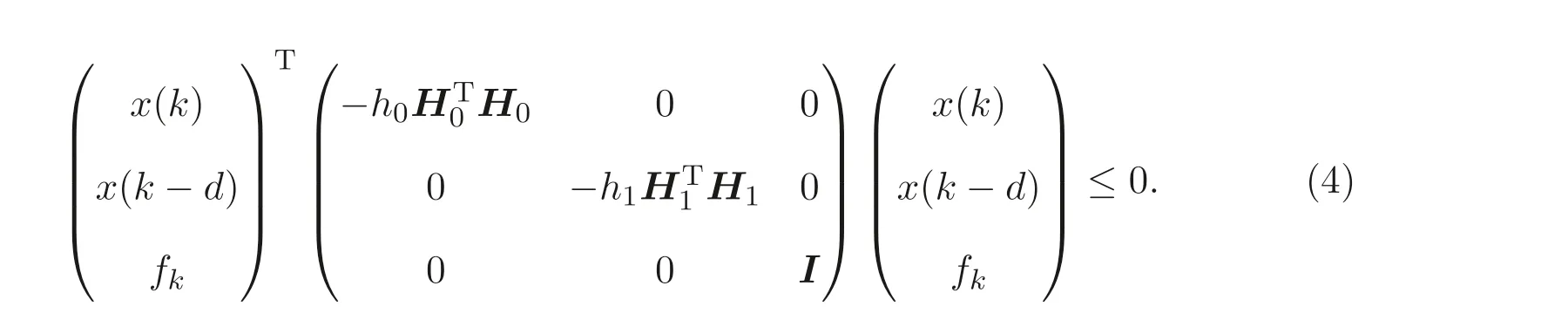
利用S-procedure, 将不等式(3)-(4) 结合起来等价于下列不等式成立:

根据Schur 补引理2.2 知,

其中,

根据引理2.1 可知,

即

根据Schur 补引理2.2 知,

同理, 不等式(8) 等价于下列不等式

通过以上推导, 命题得证.

4 鲁棒控制器设计

在实际控制系统中, 系统往往具有时滞性, 不确定性及外部扰动等特点, 考虑如下不确定时滞系统

其中,u(t)∈Rm是系统的输入, ΔA,ΔAd,ΔB为参数不确定项, 满足如下条件:

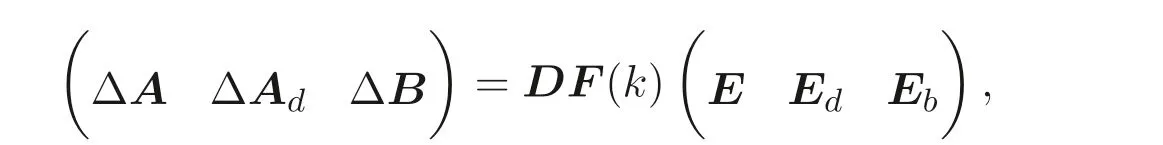
其它项满足系统(1) 中设定的条件.

设计一个状态反馈控制器u(k)=Kx(k), 使得如下闭环系统渐近稳定:

其中, ˜A=A+BK+ΔA+ΔBK,˜Ad=Ad+ΔAd.

定理4.1如果存在矩阵P>0, Q>0,K及正数ε>0 满足下列不等式

证明由定理3.1 可知, 闭环系统(11) 为渐近稳定的一个充分条件是

用A+BK替换不等式(2) 中的矩阵A, 同时用E+BbK替换不等式(2) 中的E, 结合定理3.1 的证明过程可得不等式(13) 等价于下列不等式成立:

其中,X=A+BK,Y=E+BbK.

5 结束语

本文针对一类含非线性项的不确定离散时滞系统的稳定性问题进行了研究, 在非线性项满足一定约束条件下进行了稳定性分析, 以线性矩阵不等式形式给出了系统渐近稳定的充分条件, 从而使得系统的稳定性条件便于实现. 同时, 进一步获得了闭环系统渐近稳定的充分条件, 设计出了不确定离散时滞系统的状态反馈控制器, 定理4.1 的理论证明保证了状态反馈控制器设计的有效性.