代数函数域上的局部恢复码
2021-07-23颜好胡万宝陈子星
颜好, 胡万宝, 陈子星
(安庆师范大学数学与计算科学学院, 安庆 246133)
1 引言
传统的大型存储体系依赖于通过块复制来提供系统的可靠性, 复制的缺点是存储开销大. 擦除编码技术以相当小的存储开销实现了更高的数据可靠性, 局部恢复码(LRC码) 是擦除编码的一种, 它极大地提高了分布式存储系统的可靠性和有效性[1].
虽然现代存储系统允许几个符号丢失的情况出现, 但到目前为止, 一个符号丢失的情况更常见, 因此系统应重点设计一个符号丢失的精确恢复. 在系统中一个符号丢失的精确恢复效率, 可以通过三个不同的指标来量化, 每个指标都与不同的存储系统和应用相关, 已经有许多论文在这三个指标下考虑精确恢复问题, 即读取位的数量[2]、恢复带宽[3-6]、局部化参数r(参与恢复过程符号的个数), 关注的是局部化参数r[7-8]. 对于一个局部恢复码, 如果一个符号丢失, 可以通过至多r个符号来恢复. 局部恢复码的精确定义如下[9]:
定义1.1设C是Fq上的[n,k]线性码,如果对于每个i ∈{1,2,··· ,n},存在r个元素的子集Ii ⊆{1,2,··· ,n}{i}和一个函数φi:Frq →Fq使得对于每个码字x ∈C有xi=φi(xj1,xj2,··· ,xjr), 其中j1 如果C是(n,k,r) LRC 码, 则C的最小距离满足 若(1) 式成立, 称C是距离最优的(n,k,r) LRC 码. 当r=k时, (1) 式是著名的singleton 界. 若等式成立, 即 则称码C是MDS 码. 每个坐标重复两次得到的长度为2k的线性码是局部化参数为1的LRC 码. 另外, 整个码字可以通过接收除丢失符号之外的k个符号来确定, 因此局部化参数1≤r ≤k[10]. 文献[7] 构造了一族最优的(n,k,r) LRC 码, 与传统的MDS 码一样, 在这族LRC 码中, 码长受到了字符集大小的限制, 即要求n ≤q. 为了突破这一限制, 自然地, 可以想到利用代数曲线或者代数函数域来构造局部恢复码. 文献[10] 利用了G-S 曲线和Hermite 曲线等有理光滑绝对不可约曲线构造了LRC 码. 因为代数曲线涉及代数几何等复杂数学知识, 诸如曲线映射, 描述起来甚是繁杂. 而对于在有理光滑绝对不可约曲线上构造的局部恢复码, 都可以等价地利用单变量的代数函数域来构造,使得描述更直接,码长也可以突破字符集的大小的限制.因此,相比文献[10]的方法,利用代数函数域构造局部恢复码更具实际意义. 接着, 将构造方法应用于广义Hermite函数域, 得到了一类广义Hermite 函数域上的局部恢复码. 进一步地, 通过构造子码的方式明显地改进了广义Hermite 函数域上的局部恢复码的最小距离的下界. 定义2.1设x ∈F是K上的超越元, 一个扩域F ⊇K使得F是K(x) 的有限代数扩张, 则称F/K是K上单变量的代数函数域. 设P是F/K的一个位(place),OP是它的赋值环,由于P是OP的一个极大理想,因此OP/P是一个域, 记为FP, 又由于K ⊂OP且K ∩P={0}, 因此OP →OP/P诱导出了K到OP/P的一个嵌入. 设F/K是满常域为K的代数函数域,PF是F中位的集合, 次数为1 的位称为有理位,g(F) 表示F的亏格. 定义2.3设G是F的除子, 黎曼洛赫空间定义为 它是K上有限维的向量空间,它的维数为l(G)≥degG+1−g(F),当degG>2g(F)−1时,l(G)=degG+1−g(F). 命题2.1设x ∈FK, 则deg(x)=0, deg(x)0=deg(x)∞=[F:K(x)]. 定义2.4设F′/F是函数域的代数扩张且P ∈PF, 如果F中存在P的一个扩张P′∈PF′, 使得分歧指数e(P′|P)=[F′:F], 则称P在F′/F是完全分歧的. 定义2.5设F′/K′是F/K的代数扩张, 对于一个位P ∈PF, 定义它关于F′/F的上范数为 命题2.2设代数函数域F=Fqs(x,y) 满足 其中p(y)∈Fqs[y], 设E=Fqs(y), 则 (a) [F:E]=qs−1,Fqs是F的满常域; (b)x,y的公共极点是Q∞; (c) (y)∞=qs−1Q∞, (x)∞=(qs−1+qs−2)Q∞; (d)F中有N=1+q2s−1个次数为1 的位, 其中一个是x的极点Q∞, 另外, 对于所有的α ∈Fqs, 有α1+q+α1+q2+···+αqs−2+qs−1=β ∈Fqs且存在qs−1个不同的元素λ ∈Fqs使得λqs−1+···+λq+λ=β, 因此对于这样的(λ,β) 存在次数为1 的位Pλ,β ∈PF使得x(Pλ,β)=λ且y(Pλ,β)=β. 定义2.6设F/Fq是亏格为g(F)的代数函数域,P1,P2,··· ,Pn是F/Fq中互不相同的有理位,D=P1+P2+···+Pn,G是F/Fq的一个除子使得supp(G)∩supp(D)=∅, 则关联D和G的代数几何码定义为 对于m ∈Z, 取G=mQ∞, 定义一点广义Hermite 码为Cm:=CL(D,mQ∞), 其中D是广义Hermite 函数域F/Fqs上次数为1 的位(Q∞除外) 的和, 码Cm称为广义Hermite 码. 命题2.3设dm是码Cm的最小距离, 则 (a) 若m=aqs−1,0≤a ≤qs, 则dm=n −m; (b) 若m=aqs−1+b(qs−1+qs−2),0≤a ≤qs −qs−1−qs−2, 且0≤b ≤qs−1,则dm=n −m; (c) 若m=q2s−1−qs−1+b,0≤b ≤qs−1, 则dm=qs−1. 在文献[10] 中利用有限域上的代数曲线构造局部恢复码要求K(X)=K(Y)(x) 满足方程xr+1+brxr+···+b0=0, 其中bi ∈K(Y). 本节利用代数函数域构造局部恢复码不受这一条件的限制. 下面介绍代数函数域上局部恢复码的构造: 设F/Fq,E/Fq是满常域为Fq的代数函数域,F为E的扩域且[F:E] =r+1,设S={P1,P2,··· ,Pm}是E中m个有理位的集合, 且每个Pi,i= 1,2,··· ,m在F/E中是完全分裂的, 即对于E中每个Pi都存在r+ 1 个次数为1 的扩张Pi1,Pi2,··· ,Pi(r+1), 设P={Pij,1≤i ≤m,1≤j ≤r+1}, 则|P| =m(r+1),P的划分A={A1,A2,··· ,Am}, 其中Ai={Pi1,Pi2,··· ,Pi(r+1)},i=1,··· ,m. 1.女子贫民院-Chiu Chi Yuan(石碑胡同(Shih Pei), Hsi Ssu Pai Lou) 设D是E中的除子使得supp(D)∩S=∅,f1,f2,··· ,ft是L(D) 在Fq上的一组基, 设x ∈F使得1,x,··· ,xr−1在E上线性无关,x(Pij) 对于每个Ai中的有理位是互不相同的, 其中i=1,··· ,m, 定义函数空间 定义映射 记这个映射的像为C(P,V). 定理3.1上述定义的码C(P,V) 是Fq上的(n,k,r) LRC 码, 若 则其参数为n=m(r+1),k=rt, d ≥n −(r+1)deg(D)−(r −1)deg(x)∞. 证明显然码长n=m(r+1), 下面证明fjxi,j= 1,··· ,t,i= 0,··· ,r −1 在Fq上线性无关, 若 由于1,x,··· ,xr−1在E上线性无关, 则 又由于f1,··· ,ft在Fq上线性无关, 则aij= 0, 从而fjxi在Fq上线性无关, 所以dimFq(V)=rt. 下证fj ∈L(D),fjxi至多有(r+1)deg(D)+(r −1)deg(x)∞个零点, 设零点的个数为|I|, 由于|I|≤deg(fjxi)0=deg(fjxi)F∞, 则 由于fj ∈L(D),则(fj)+D ≥0,即(fj)0−(fj)∞+D ≥0,又由于supp(D)∩S=∅,则(fj)∞≤D, 从而deg(fj)∞≤deg(D), 所以有 设g1,g2∈V,g=a1g1+a2g2̸=0,a1,a2∈Fq, 由于 则对于任意的Q ∈supp((r+1)D+(r −1)(x)∞) 有 所以从而deg(a1g1+a2g2)≤deg((r+1)D+(r −1)(x)∞), 即 所以fj ∈L(D),fjxi至多有(r+1)deg(D)+(r −1)deg(x)∞个零点. 下证eVA:(Pij) 是单射, 考虑 由于f ∈V至多有(r+1)deg(D)+(r −1)deg(x)∞个零点, 且 则f=0, 所以eVA是单射, 显然也是满射, 从而 由于C(P,V) 是线性码, 则最小距离d ≥n −(r+1)deg(D)−(r −1)deg(x)∞. 下面给出修复方案: 假设Pα ∈Ai,i ∈{1,2,··· ,m}对应的符号为Cα=f(Pα) 丢失, 令 其中0≤i ≤r −1, 设f ∈L(D),Pi是E中的位,Pij,j=1,··· ,(r+1) 是Pi的扩张,且deg(Pij)=1, 声明f(Pij)=f(Pi), 由f(Pi)∈Fq可知, 存在a ∈Fq使得 从而有f −a ∈Pi ⊆Pij, 因此 即f(Pij)=f(Pi). 对于任意的Pβ ∈Ai有 由于deg(δ(x))≤r −1, 且{x(Pβ)}Pβ∈Ai{Pα},i ∈{1,2,··· ,m}是互不相同的, 丢失的符号可以通过Ai中其余r个位置Pβ ∈Ai{Pα}对应的符号通过插值得到, 一旦δ(x)确定, 则丢失的符号为δ(x)(Pα), 因此C(P,V) 是(n,k,r) LRC 码, 其中参数为 下面将此构造方法应用于广义Hermite 函数域去构造局部恢复码. 考虑代数函数域F=Fqs(x,y) 满足 当s=2 时, 广义Hermite 函数域就变成了Hermitian 函数域. 设E=Fqs(y), 则[F:E]=qs−1, 设qs−1=r+1,l=qs, 由命题2.2 知, 设由Fqs带来的有理位的集合为S1={P1,P2,··· ,Pl}, 每个Pi,i= 1,2,··· ,l在F/E中是完全分裂的,Pi1,Pi2,··· ,Pi(r+1)是Pi上的有理位, 设F中有理位的集合为 则|P|=l(r+1),P的划分为A={A1,A2,··· ,Al}, 其中 矛盾, 因此1,y,··· ,yt在Fqs上线性无关. 又由于 则l(D)=deg(D)+1−g(E)=t+1, 从而1,y,··· ,yt是L(D) 在Fqs上的一组基. 由于[F:E]=qs−1, 则1,x,··· ,xr−1在E上线性无关,x(Pij) 对于Ai,i=1,··· ,l中的有理位是互不相同的, 定义函数空间V=〈xiyj,i= 0,··· ,r −1,j= 0,··· ,t〉, 定义映射: 记这个映射的像为C(P,V). 应用定理3.1 得到一类局部恢复码, 其参数如下: 定理4.1上述定义的码C(P,V) 是Fqs上的(n,k,r) LRC 码, 其中参数为 定理4.1 中最小距离的下界利用广义Hermite 码的一些性质在某些特殊的情况下可以得到改进. 事实上, 对于广义Hermite 码Cm, 选取适当的m使得V ⊆L(mQ∞),则C(P,V)⊆Cm, 由子码的性质得dLRC≥dm, 由于 则t ≤qs −qs−1−qs−2+2, 下面就以t=qs −qs−1−qs−2+2,q> 2 情况来探讨码C(P,V) 的最小距离的下界的改进思想. 定理4.2若t=qs −qs−1−qs−2+2,q>2, 则定理4.1 最小距离的界为 较(5) 式的距离改进了(q −2)qs−2. 证明取m=tqs−1+(qs−1−2)(qs−1+qs−2), 则C1(P1,V1)⊆Cm, 要证 只需证明xiyj ∈L(mQ∞), 其中i=0,··· ,r −1,j=0,··· ,t. 由 可得, (xiyj)0−(xiyj)∞≥−mQ∞, 从而有(xiyj)≥−mQ∞, 即(xiyj)+mQ∞≥0, 因此xiyj ∈L(mQ∞). 下面计算cm的最小距离dm. 若t=qs −qs−1−qs−2+2, 则 其中b=qs−1−2qs−2, 显然0 则dLRC≥dm=qs−1. 下面比较n −m与dm的大小. 当t=qs −qs−1−qs−2+2 时,n−m=n−qs−1t−(qs−1−2)(qs−1+qs−2)=2qs−2,而dm=qs−1, 因此较(5) 式的距离改进了qs−1−2qs−2=(q −2)qs−2. 证毕. 注4.1从定理4.2 可以看出, 当q>2 时, (5) 式的最小距离的界被明显地改进. 本文利用代数函数域构造出了局部恢复码, 并在广义Hermite 函数域上得到一类局部恢复码, 又通过子码的方式改进了广义Hermite 函数域上的局部恢复码的最小距离的下界. 本文针对的是一个符号丢失的精确恢复, 后面, 将扩展本文的构造方法至多个符号丢失的精确恢复, 以及构造代数函数域上具有多重恢复集的局部恢复码. 广义Hermite 曲线既是Kummer 曲线, 也是Artin-schreier 曲线, 因此更多的代数曲线可以得到更多的局部恢复码.

2 相关准备
2.1 代数函数域[11]



2.2 广义Hermite 函数域

2.3 代数几何码

3 在代数函数域上构造局部恢复码


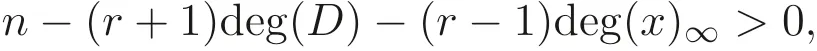















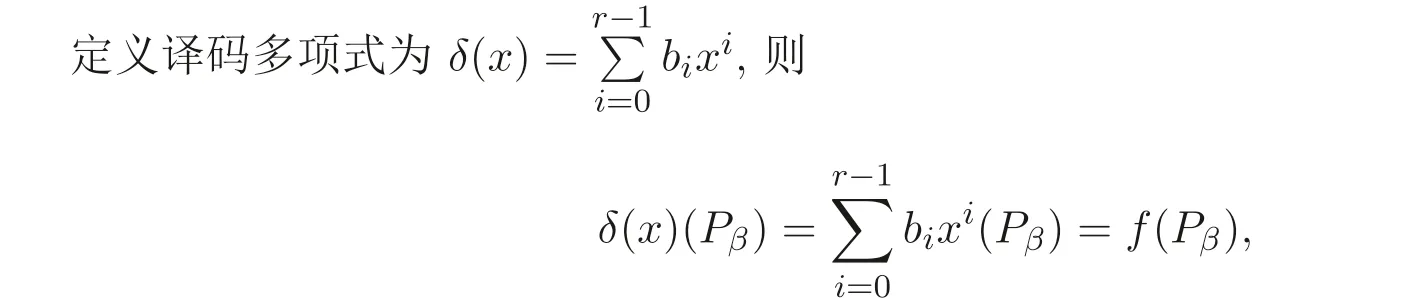

4 广义Hermite 函数域上的局部恢复码


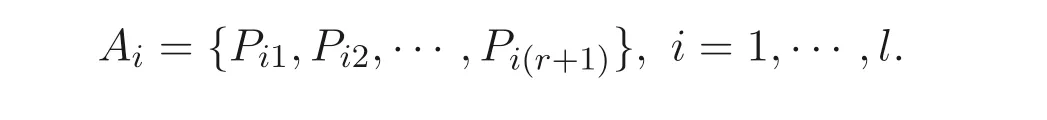



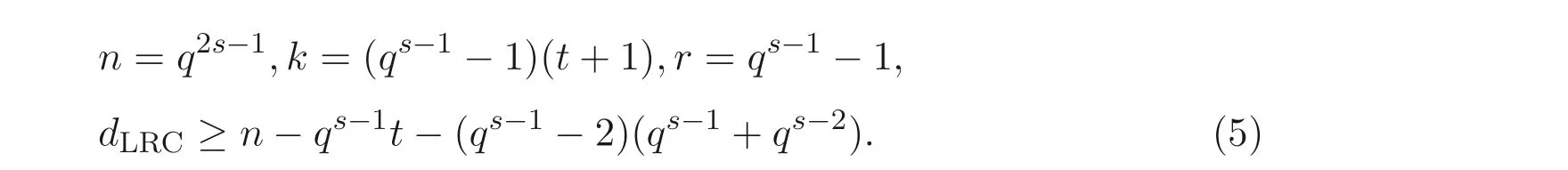






5 结束语
