基于遗传算法-支持向量机的滑坡渗透系数反演

胡 鹏，文 章，胡新丽，张玉明

（1.中国地质大学(武汉)环境学院，湖北 武汉 430074；2.中国地质大学（武汉）工程学院，湖北 武汉 430074；3.潍坊科技学院建筑与艺术学院，山东 潍坊 262700）

库水位的涨落改变坡体力学平衡和软化岩层，决定坡体内渗流场的变化，对库岸滑坡稳定性有着显著影响[1]。因此，研究库岸边坡渗流场变化对研究库岸边坡变形演化过程具有重要意义[2−4]。滑坡岩土体渗透系数的求解是研究滑坡渗流场及渗流场变化引起的多场响应的前提，常见的渗透系数获取方法有原位试验和室内试验。然而，大型滑坡岩性组成较为复杂，试验结果随取样位置不同而存在较大随机性，且难以对滑坡深部的岩土体进行原位试验，因此测试结果往往仅具有参考性，不能反映岩层整体的渗透性质，无法直接用于数值模拟应用。随着机器学习方法和优化算法的发展和应用，利用反演法求解渗透系数受到了许多学者的青睐。

构建变量之间的映射关系是参数反演的前提，支持向量机（support vector machine,SVM）模型已被证明在构建非线性函数映射关系上具有很高的精度[5−7]。Prasad等[8]提出了一种遗传算法和数值模型结合的全局优化方法，并应用于马西右岸运河（MRBC）项目区渗透系数和补给参数的估算。魏进兵等[9]建立了泄滩滑坡饱和－非饱和渗流有限元计算模型，结合滑坡体地下水位监测资料，采用BP（back propagation）神经网络反演泄滩滑坡各地层渗透系数。崔皓东等[10]利用三维渗流场有限元结合遗传算法，建立二滩高拱坝坝基渗流场反演模型，通过测点水位反演获得了坝基渗透系数。姜谙男等[11]利用支持向量机建立水头与渗透系数之间的映射关系，以识别误差目标函数为适应值，通过粒子群优化算法反馈搜索得到了渗透系数。倪沙沙等[12]针对糯扎渡高心墙堆石坝，通过支持向量机建立渗透系数与水头之间的映射关系，参照大坝测压点水头，利用粒子群优化算法对大坝渗透系数进行了反演。向家松等[13]对比分析了不同地下水监测频率和时长对滑坡渗透系数反演结果的影响。

此外，部分学者还将机器学习与优化算法结合的方法应用于反演岩土体力学参数和变形参数。李端有等[14]以清江杨家槽滑坡为例进行研究，提出了将均匀设计、遗传算法与BP神经网络结合起来应用于滑坡反分析的方法，依据实测位移对滑坡岩土体力学参数进行了反演。Su等[15]利用支持向量机建立了大坝的变形预测模型，通过粒子群算法实现大坝变形预测模型的参数优化。Sun等[16]在三峡库区三门洞滑坡力学参数试验和位移观测资料的基础上，通过BP神经网络构建滑坡岩土体力学参数与位移量之间的关系，在此基础上，利用遗传算法反演得到了滑坡岩土体的力学参数。

但现有研究大多是利用某一时刻的水位或变形来反演相关参数，而库岸边坡水位变化实际上是一个动态的过程，因此，本文利用动态监测水位建立了一个新的反演方法，其基本思想是：根据边坡岩性和水文地质试验，确定待求渗透系数的取值区间；利用有限元软件生成渗透系数与对应水位的学习样本，在此基础上，通过机器学习方法构建水位与渗透系数的映射关系；最后，代入实测动态水位求解相应的岩土介质渗透系数。本文利用该方法反演了马家沟滑坡岩土体的渗透系数，为马家沟滑坡渗流场研究提供参数支持。

1 学习方法简介

1.1 支持向量机

支持向量机是机器学习算法的一种，1964年由Vapnik等[17]在统计学习理论的基础上提出，该算法基于结构风险最小化原理，对高度复杂的非线性问题具备良好的适应性，可以用于解决分类和回归问题。

对于线性回归问题，假设n维空间训练样本集{Xi，Yi}（Xi∈Rn，Yi∈R，i=1，2，···，k，k为样本个数），构造最优线性函数：y=w·x+b，使得所有训练样本在精度ε内都能用该线性函数拟合，且使得所有样本点产生的总偏差最小，引入允许拟合误差松弛因子ξi、ξi∗，目标函数如下[15]：

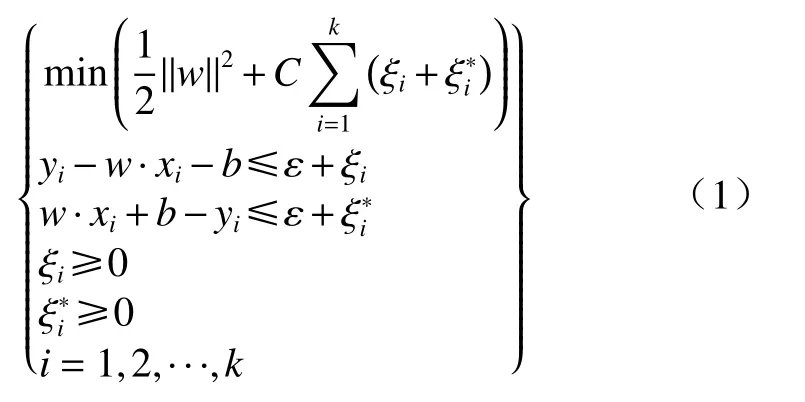
式中：C—惩罚因子，控制对超出误差ε的样本的惩 罚程度；

w—超平面函数法向量；

b—超平面函数截距。

通过构建拉格朗日函数，得到对偶形式：

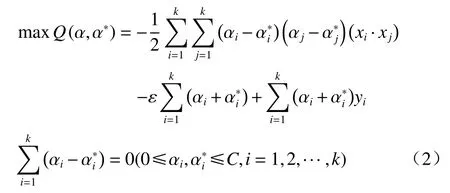
得到拟合样本集的估计函数公式：

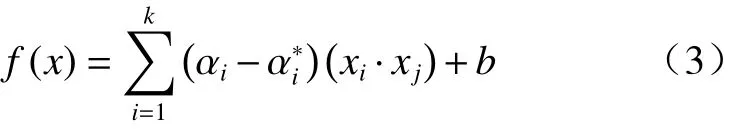
对于非线性回归问题，通过映射的方法将原始样本数据变换到高维特征空间（H），在高维特征空间中设计线性回归支持向量机，再通过原空间的函数内积运算，得到在原空间的非线性回归的估计函数。

不同的核函数能构造输入空间不同类型的非线性决策面，常见的满足Mercer条件的核函数主要有线性核函数、多项式核函数、多层感知机核函数（Sigmoid）、径向基核函数（Radial Basis Function,RBF）。其中，径向基核函数能实现非线性映射，参数较少且具有较宽的收敛域，适合作为通用模式识别的核函数。因此，本文使用径向基核函数。

1.2 遗传算法

遗传算法（genetic algorithm，GA）是一种基于自然选择机理的全局优化求解方法，20世纪70年代由美国学者Holland[17]提出，它模拟自然界中生物自然选择和遗传过程中发生的遗传、杂交和变异现象。遗传算法是一种基于“适者生存”的高度并行、随机和自适应的优化算法，通过复制、交叉、变异将解编码表示的“染色体”群一代代不断进化，最终收敛到最适应的群体，从而求得问题的最优解。其优点是原理和操作简单、通用性强、不受限制条件的约束，且具有隐含并行性和全局解搜索能力，在组合优化问题中得到广泛应用。

本文中，利用遗传算法优化寻找支持向量机学习效果最好的参数，即利用遗传算法优化支持向量机模型参数（遗传算法终止代数设置为50，初始种群数量设置为20，以向量机预测的渗透系数和样本渗透系数值差值最小为适应度函数，计算寻找最优的核函数参数），使得支持向量机模型达到最好的数据样本训练效果。

2 基于遗传算法-支持向量机（GA-SVM）的马家沟滑坡渗透系数反演

2.1 马家沟滑坡概况

三峡库区沿岸地质条件较复杂，滑坡、崩塌众多，对周边居民的生命财产安全有重大影响[18]。马家沟滑坡位于湖北省秭归县，在长江支流吒溪河的左岸，是三峡库区典型的库岸边坡之一（图1）。马家沟滑坡自2003年三峡库区初次蓄水至135 m后发生明显变形，坡体后缘出现大规模的拉裂缝；在2007年做了抗滑桩工程措施，但由于深层滑带的存在以及库水位的周期涨落作用，滑坡的变形并未停止[19−20]。中国地质大学工程学院胡新丽课题组对马家沟滑坡进行了充分的工程勘察和长期的野外综合观测，掌握了马家沟滑坡的地质情况和多年综合观测资料，具备良好的研究基础。马家沟滑坡东西向展布，整体呈缓坡型，平均坡度为15°；滑坡滑动方向为291°，基本垂直于长江支流吒溪河。滑坡纵向长度为540 m，前后缘宽度分别为150，210 m（图2）。

图1 马家沟滑坡全貌图（据文献[20]）Fig.1 A close-up view of the Majiagou landslide（from Ref.[20]）

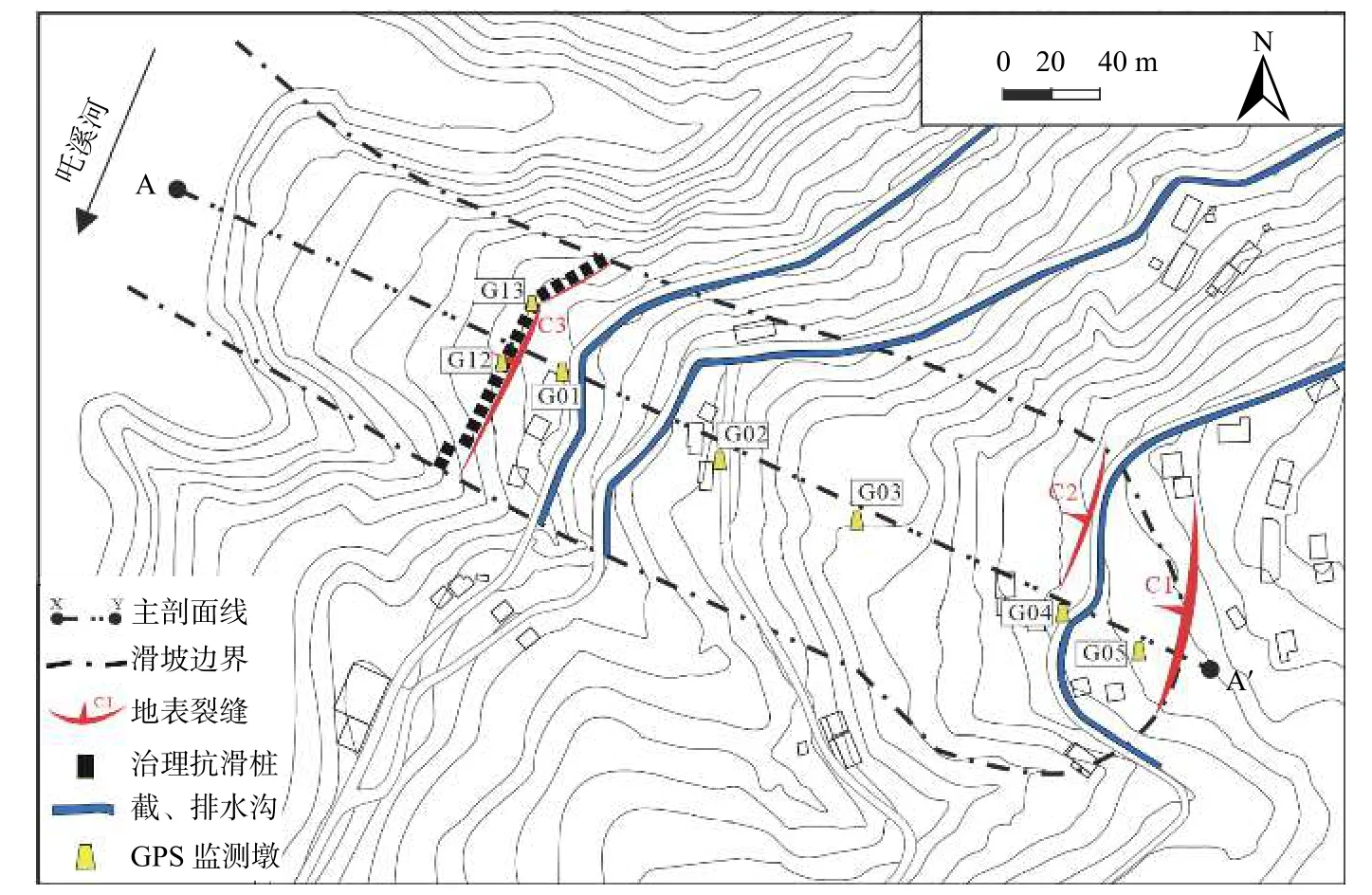
图2 马家沟滑坡平面图（据文献[20]）Fig.2 Map of the Majiagou landslide（from Ref.[20]）

滑坡前缘滑面位置在最低水位145 m以下，后缘高程为280 m。根据工程地质勘察，确定滑坡边界范围，计算出滑坡面积约为9.68×104m2，滑坡深层滑带深度约30 m，初步估计失稳体积约为2.52×106m3。

由图3可见，马家沟滑坡岩土体由第四系堆积物和下部的基岩构成。第四系松散堆积层广泛分布于坡体浅中层，一般厚度为8～15 m，总体上由滑坡后缘向前缘厚度递增；堆积物根据成因类型可以分为冲洪积物、崩坡积物、残坡积物，主要岩性为粉质黏土和碎石土；滑坡下部基岩地层主要是侏罗系上统遂宁组J3s，岩性以灰白色长石石英砂岩、细砂岩为主，夹有紫红色砂岩和粉砂质泥岩，力学强度较低，且泥岩夹层遇水易软化，是三峡地区易滑地层之一；岩层层面产状为270°～290°∠25°～30°，节理较发育，以微风化为主，上部岩石风化较严重，根据破坏模式和滑体成分，该滑坡属于顺层岩质滑坡。图中，G01、G02、G03、G04、G05为地表位移监测点，OFS1、OFS2、OFS3、JC1、JC3、JC6、JC8为深部位移监测点，JC1、JC3、JC8布设了水位计和渗压计，同时可以监测地下水位。

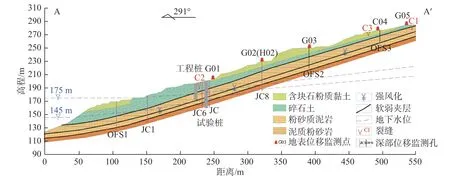
图3 马家沟滑坡剖面图Fig.3 Profile of the Majiagou landslide

2.2 马家沟滑坡模型的建立

选取马家沟滑坡主剖面的前半部分，利用有限元软件Geo-Studio建立马家沟滑坡二维模型（图4），模型水平长度为385 m，垂直高度为230 m。第四系堆积层主要由含块石粉质黏土和碎石土组成，由于黏土仅分布于坡面前缘小部分和坡体后缘潜水面以上部分，因此在数值模型中将该层岩性简化为碎石土。下部基岩依据风化程度，在数值模型中以软弱夹层为界将基岩地层分为两层，上层为风化较严重的砂岩夹粉砂质泥岩，下层为稳定基岩。因此，滑坡数值模型中岩土介质根据岩性从坡体表面向内分别概化为碎石土、砂岩夹粉砂质泥岩（强风化基岩）和稳定基岩三种不同的岩土材料[20]。

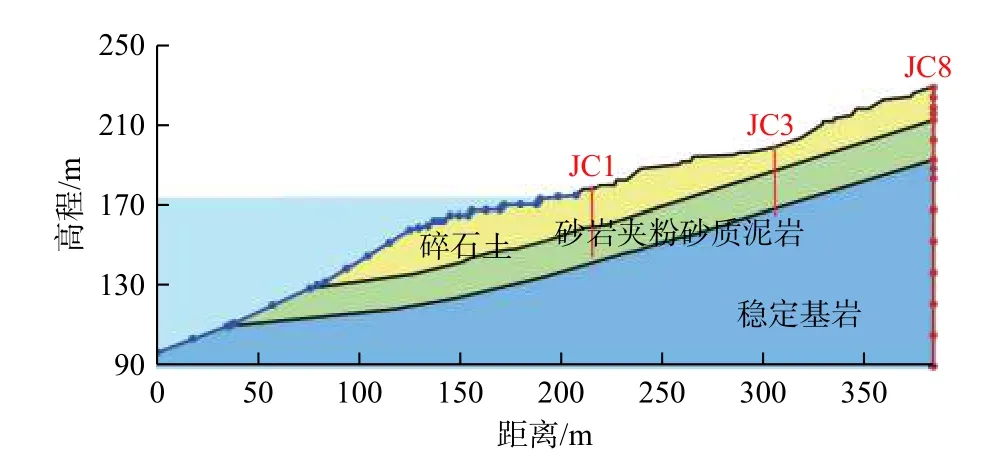
图4 马家沟滑坡数值模型Fig.4 Numerical model of the Majiagou landslide

各层岩土材料的非饱和渗流特性主要与渗透系数函数和土水特征曲线有关，模型中土水特征曲线选择软件中内置相应岩性的样本函数，输入饱和体积含水量（约为岩土层的孔隙率，见表2）得到，具体如图5所示。随后选择Fredlund和Xing方法估计渗透系数函数，结合土水特征曲线及饱和渗透系数得到渗透系数函数。数值模型左边界中库水位以下设置为定水头边界，水头大小等于随时间变化的库水位，右侧边界设置为定水头边界，水头大小等于随时间变化的监测孔JC8的水位，其他边界设置为无流量边界。在整个滑坡模型上有3个水位监测孔，从河岸往滑坡后缘依次为JC1、JC3、JC8（图3）。模型的初始水位根据库水位和三个观测水位相连而成，初始水位选择2013年1月16日马家沟滑坡初次监测的水位。

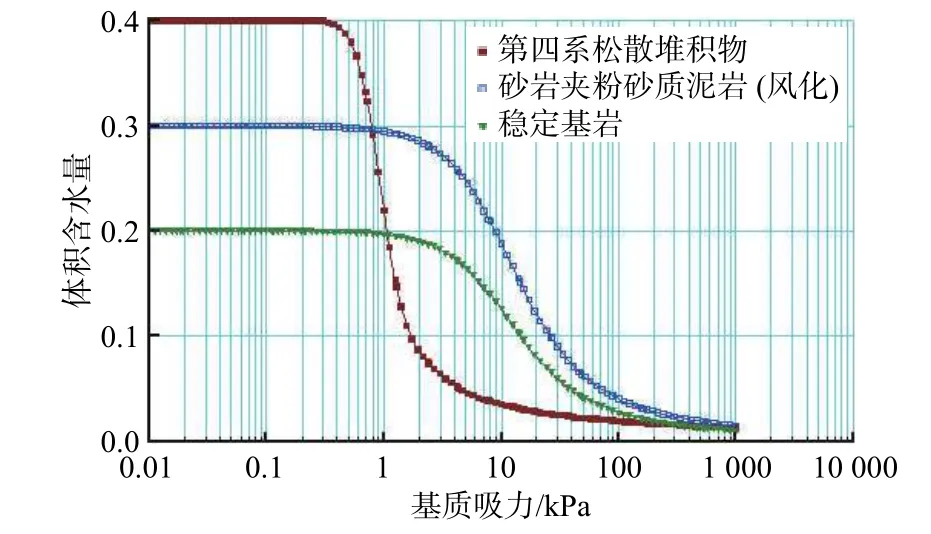
图5 马家沟滑坡模型土水特征曲线Fig.5 Soil-water characteristic curve of the Majiagou landslide

本文中地下水渗流问题的数学模型如下：

式中：kx、ky—x、y方向的渗透系数，土体非饱和时是体积含水量和基质吸力的函数/（m·s−1）；

H—总水头/m；

Q—施加的边界流量/（m3·s−1）；

mw—土水特征曲线的斜率；

γw—水的容重/（N·m−3）；

t—时间/s；

Γ1、Γ2—第一类、二类边界；

n—边界的外法向量方向；

T—导水系数/（m2·s−1）；

q—单宽流量/（m·s−1）。

根据马家沟滑坡的岩性剖面，待反演的岩土体岩性组成从地表向下依次为第四系松散堆积层（碎石土）、强风化砂岩夹粉砂质泥岩（含裂隙基岩）以及稳定基岩。图6为现场入渗试验布点情况，参考现场入渗试验结果（表1）中各试验段岩性对应渗透系数大小，结合文[20]中所取渗透系数范围和模型试算结果，给定三种岩土体的渗透系数数量级范围，见表2。

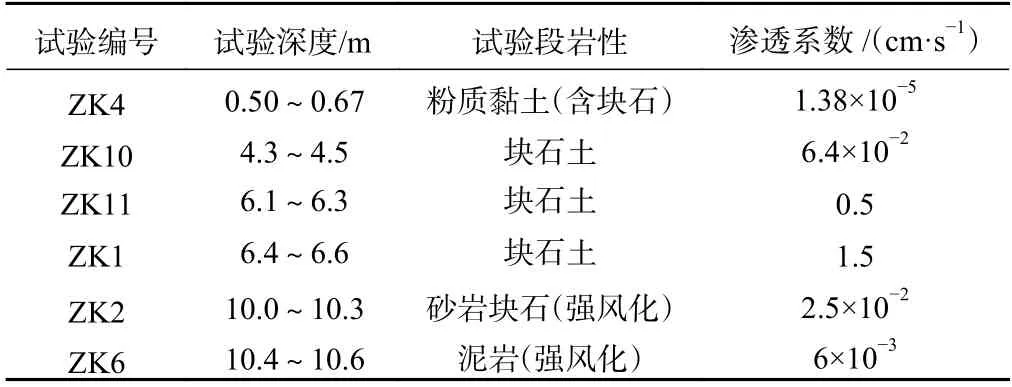
表1 马家沟滑坡入渗试验结果Table 1 Infiltration test results for the Majiagou landslide

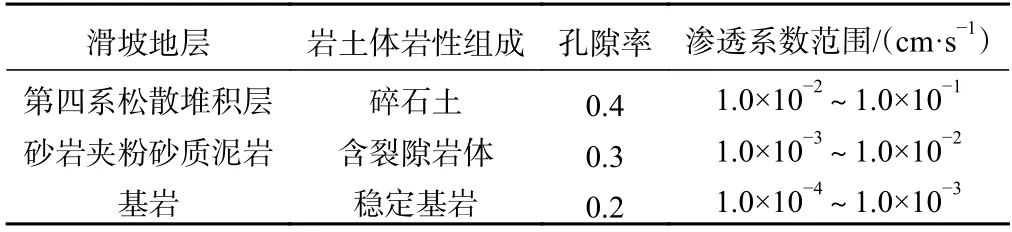
表2 马家沟滑坡岩土体渗透系数取值范围表Table 2 Range of K of rock and soil for the Majiagou landslide

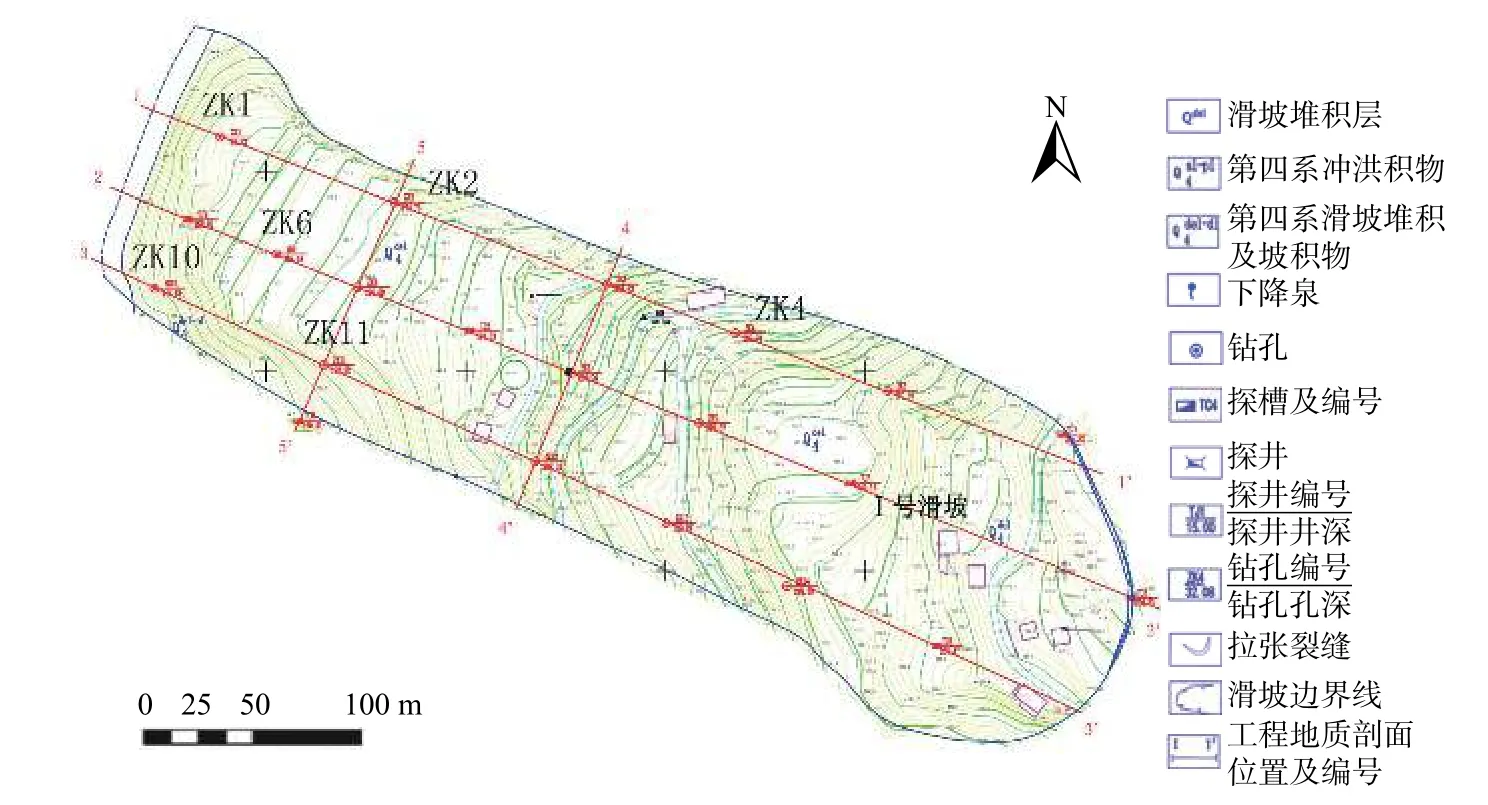
图6 入渗试验布点图Fig.6 Infiltration test location for the Majiagou landslide

依据滑坡不同岩土体渗透系数取值范围，设计碎石土K1（第四系堆积物）、含裂隙岩体K2（强风化砂岩夹粉砂质泥岩）、基岩K3（稳定基岩）3个因子，每个因子在取值范围内取5个值，利用SPSS设置正交试验25组（表3）。将构造的渗透系数组合代入有限元软件进行模拟计算，获取相应监测点JC1、JC3的水头值，得到25组渗透系数及其对应模拟水位值H1（JC1）、H2（JC3）的样本。

2.3 基于GA-SVM方法的滑坡渗透系数反演

将表3中的渗透系数-水位数据作为机器学习的样本，应用台湾大学Lin Chih-Jen开发的Libsvm（A Library for Support Vector Machines）工具箱[21]和李洋改进的LIBSVM faruto Version版本[22]，通过Matlab调用支持向量机模型进行计算，模型的训练效果见图7。图7（a1）（b1）（c1）分别表示K1、K2、K3训练过程中适应性曲线的变化，可以看到进化代数在20代之后，适应度值已基本接近于0，说明寻优的速度快，效果好；图7（a2）（b2）（c2）分别表示K1、K2、K3的训练效果，图中均方差（MSE）表示各数据误差平方和的平均数，其值越小表示预测值越接近实际值；线性回归决定系数（R2）表示自变量和应变量的相关关系，越接近于1，表示相关关系越强，预测性越好。可以看到，GA-SVM支持向量机反演渗透系数的方法具有较好的学习预测效果。

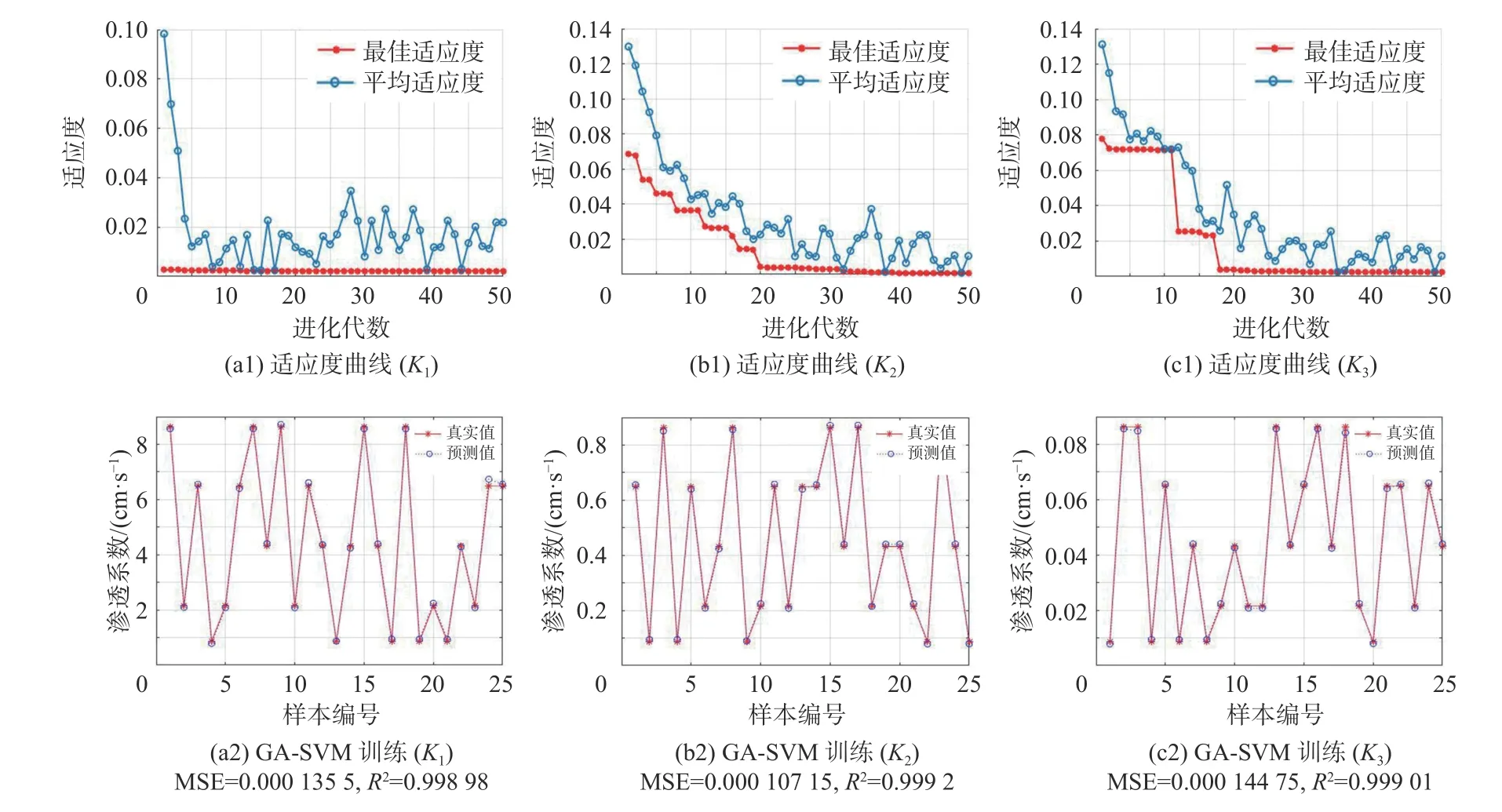
图7 支持向量机训练结果图Fig.7 Support vector machine training results

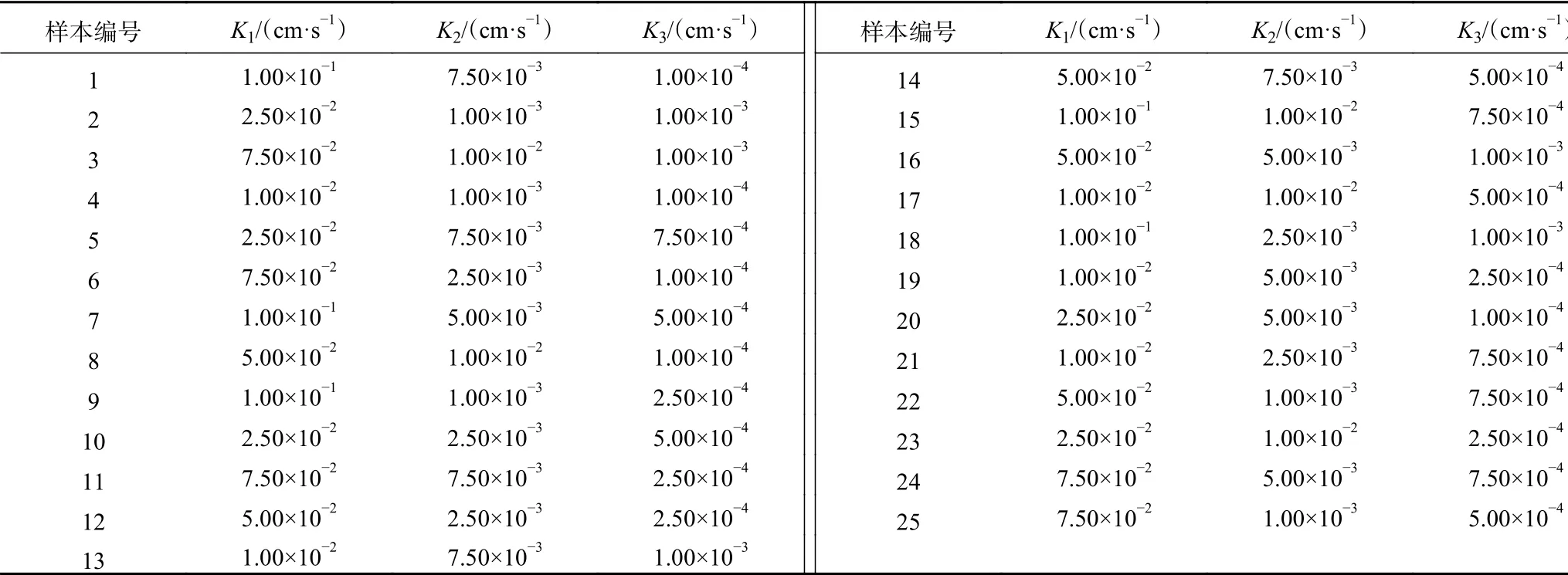
表3 数值模型计算方案表Table 3 Calculation schemes with the numerical model

将实际观测水位输入到训练后的支持向量机，得到滑坡岩土体的渗透系数（表4）。将基于支持向量机反演得到的滑坡岩土体渗透系数代入数值模型中，得到不同时刻的地下水水位。

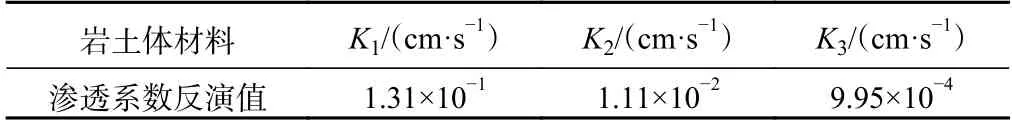
表4 滑坡岩土体渗透系数反演值Table 4 Inversion values of K of landslide rock and soil mass

图8为马家沟滑坡地下水水位监测情况，监测周期为2013年1月16日至2017年8月7日，监测频率约为2月/次。本文为了减小模型计算时间和数据量，选取2013年1月16日到2014年12月10日的监测数据来与模拟水位进行验证对比。

图8 马家沟滑坡地下水水位监测结果Fig.8 Monitoring results of groundwater levels of the Majiagou landslide

图9为马家沟滑坡钻孔监测水位与模拟水位对比结果，可以看出，滑坡体监测孔的实测水位值与模拟水位值很接近，说明反演结果比较可靠，基于GA-SVM支持向量机的反演方法具有良好的效果，准确可行。最终得到参数反演的结果为：K1=1.31×10−1cm/s，K2=1.11×10−2cm/s，K3=9.95×10−4cm/s。

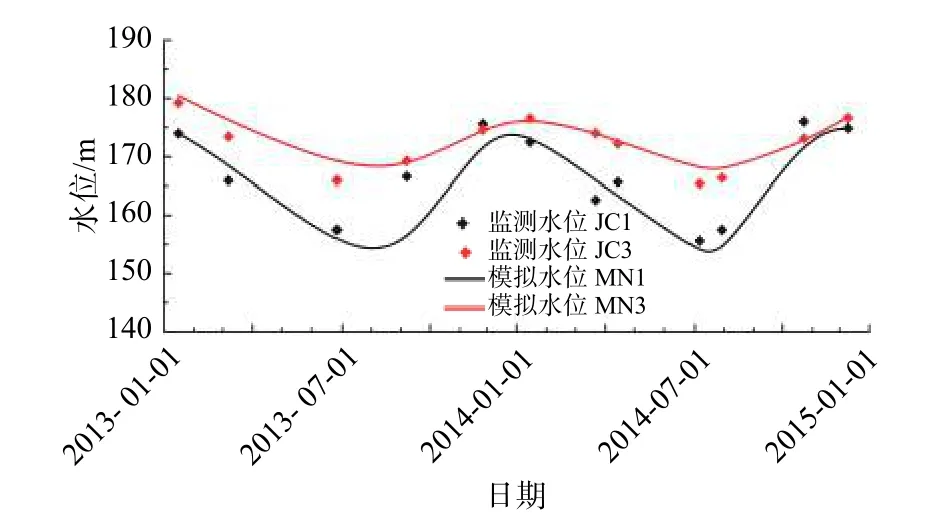
图9 监测孔地下水水位模拟值与实测值的对比Fig.9 Comparison of the measured values with the simulated values of groundwater levels

3 结论

（1）基于遗传算法优化的支持向量机（GA-SVM）方法具有收敛快、学习预测效果好的优点，构建的水位与渗透系数映射关系非常精准，且训练后的支持向量机具有很好的泛化预测能力，能够预测动态水位对应的岩土体渗透系数，代入实测水位，得到马家沟滑坡岩土介质的渗透系数：碎石土（第四系松散堆积物）K1=1.31×10−1cm/s；含裂隙岩体（强风化砂岩夹粉砂质泥岩）K2=1.11×10−2cm/s；稳定基岩K3=9.95×10−4cm/s。（2）通过代入反演所得岩土介质的渗透系数到数值模型中，计算模拟水位，并将其与实测水位对比验证，结果表明：模拟值与实测值拟合较好，说明反演结果可信度高，方法可行性强；同时，该方法可以给滑坡岩土体力学参数、强度参数的反演提供参考。