半干旱地区地表-地下水系统水热运移与裸土蒸发研究

马稚桐，王文科，赵 明，黄金廷，卢艳莹，侯昕悦，王 一

（1.长安大学水利与环境学院，陕西 西安 710054；2.西安科技大学地质与环境学院，陕西 西安 710054）

土壤蒸散发是自然界水循环和能量平衡的重要组成部分，其中，裸地蒸发约占年平均蒸发总量的60%，很大程度地影响着地下水的形成与生态环境的演化[1−3]。土壤蒸发的动力学过程极为复杂，尤其在干旱半干旱地区[4−6]，主要受到大气条件、水文地质环境、土壤水力性质和地下水位埋深等因素的影响[7−8]。然而，近年来随着地下水位埋深的不断下降，造成了土壤盐碱化、荒漠化、生态脆弱化等一系列地质环境问题[9−12]，加剧了水资源的无效蒸发。开展不同水位埋深条件下的土壤蒸发与水分运移研究，可为生态环境保护和水资源合理开发利用提供理论依据。

国内外学者对土壤蒸发及水分运移过程进行了许多研究，杨建锋等[13]通过数值模拟方法，发现当地下水位埋深小于极限深度时，地下水在土壤水运移过程中扮演着重要的角色。Wang等[14]利用室内观测数据，基于水热耦合模型指出了地下水位不仅控制着表土蒸发过程，还能显著地改变剖面温度和水分分布特征，并对气候变化产生一定的影响。Hernandez-Lopez等[15]利用室内监测装置分析了一定水位埋深条件下土壤蒸发过程，发现水位埋深大于75 cm时近地表范围出现连续的干层，导致蒸发量急剧减少。Li等[16]基于一个封闭的室内试验，发现潜水蒸发过程受昼夜温差的影响，土壤表层附近的水汽转化使得日间蒸发量比夜间更小。Zeng等[17]将场地监测数据与水汽热耦合模型相结合，估算了土壤剖面的水分分布规律，提出干燥锋的昼夜变化是控制蒸发与降雨入渗的关键因素。Kamai等[18]应用土壤水汽传输模型，发现土壤蒸发的动力学阶段受水位埋深的控制，向上运动的水分直接影响着蒸发量的大小。

虽然，前人对于土壤水运移、蒸发量的变化特征进行了广泛的研究和验证，但结合以往研究可知目前针对不同地下水位埋深条件下土壤水通量分布及其对蒸发影响的研究较少。本文以鄂尔多斯高原毛乌素沙漠为研究区，利用原位变水位蒸渗仪监测数据，结合数值模型，建立了考虑水汽热耦合运移的数值模型，对土壤蒸发量进行估算，分析了土壤水的水分运移规律，探讨了水位埋深对土壤蒸发的影响，在此基础上深入解析了土壤蒸发的动力学阶段。

1 试验区概况

研究区位于毛乌素沙地中南部，属于典型的干旱半干旱地区，地下水位埋深约1～30 m[19]，降雨稀少，蒸发强烈，植被稀疏，生态环境极其脆弱，尤其在地下水浅埋区，蒸发是地下水消耗的主要途径。据气象站资料：该区多年平均气温5.6 ℃；年均日照时数2 600 h；年均降水量386.1 mm，主要集中在7—9月，占全年降水量的67.2%；年均蒸发量2 109.2 mm。

原位试验基地位于内蒙古乌审旗河南乡国家气象站，由2个不同地下水位埋深的变水位蒸渗仪组成。蒸渗仪埋深高度分别是305 cm（深埋深）和190 cm（浅埋深），直径60 cm，底部密封，有效防止了地下含水层的渗漏。填充介质为均匀的风积沙，该介质的毛细上升高度约为50 cm[2]。气象站提供气温、相对湿度、降雨、净辐射、气压、风速、风向等数据，时间间隔为1 h。本研究采用高精度的时域反射仪5TM（Decagon Inc,±0.02）探头对土壤体积含水率和温度进行监测，探头分别布设在剖面3，10，100 cm处。地下水位埋深使用水位监测计DI501（Diver Inc.,±0.05%）进行记录，初始水位埋深分别位于地下约2.9，0.8 m（图1），深埋深水位随时间缓慢升高，水位埋深稳定在约290 cm；然而，浅埋深水位波动明显，波动范围在0～80 cm，地下水位受降雨和蒸发的交替影响呈逐渐上升的趋势，最高地下水位可达土壤表面，随着前期降雨的影响，地下水位埋深逐渐减小。所有监测数据以5 min间隔自动记录。试验期选取蒸发较为强烈的时段2017年8月1日—10月12日。

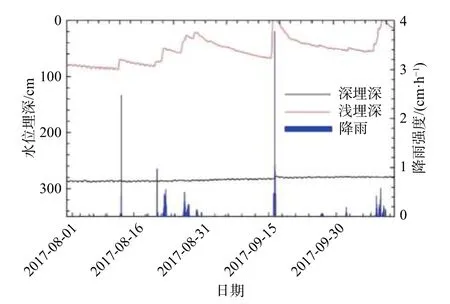
图1 监测期地下水位埋深的变化图Fig.1 Variation in water table depth during the monitoring period

2 数学模型建立

2.1 基本方程

Simunek等[20]基于有限单元法开发出关于水、汽、热耦合模型（HYDRUS-1 D），可用于模拟水、热和溶质在一维变饱和介质中的运动。土壤水流质量方程为[21]：

式中：qm—土壤水通量/（cm·s−1），通量为正值说明水 分运移方向向上，负值说明水分运移方 向向下；

ql—液态水体积通量/（cm·s−1）；

qv—汽态水体积通量/（cm·s−1）。

其中液态水体积通量为：

式中：Klh—等温液态水渗透系数/（cm·s−1）；

KlT—非等温液态水渗透系数/（cm2·s−1·K−1）；

h—水头/cm；

T—土壤温度/℃；

z—土壤深度/cm。

van Genuchten[22]提出关于非饱和渗透系数的经验公式，表达式为：

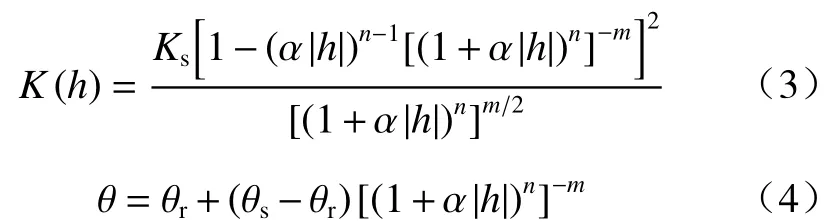
式中：n,m—拟合参数，m=1−1/n；

θs—饱和含水率；

θr—残留含水率。

汽态水体积通量为：

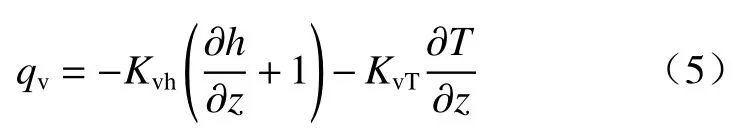
式中：Kvh—等温汽态水水力传导系数/（cm·s−1）；

KvT—非等温汽态水水力传导系数/（cm2·s−1·K−1）。

2.2 初始条件与边界条件

本研究将土柱模型概化为一维水流模型，不考虑侧向和地表径流。模型剖面高度分别设为305，190 cm，节点步长为1 cm，分别有305，190个节点。初始条件由8月1日土壤剖面不同深度的实测值经过插值得到。由于蒸渗仪底部封闭，将下边界条件设为隔水边界；大气边界作为上边界，其通量由水能平衡方程确定[23]：

式中：ρvs—地表的水汽密度/（kg·cm−3）；

ρva—大气密度/（kg·cm−3）；

rv—土壤水汽的空气动力阻力/（cm·h−1）；

rs—地表阻力/（cm·h−1）。

对于热传输，上边界设为第一类边界类型（Dirichlet type）：T(0,t)=Ttop，下边界设为第二类边界类型（Neumann type）：,z为土壤深度。

3 结果与分析

3.1 模型验证

图2和图3为2种水位埋深条件下土壤含水率和温度的实测值与模拟值。剖面浅层土壤含水率受气象因素影响波动明显，当降雨发生时，含水率迅速增大。由于包气带的滤波作用，深层土壤含水率波动不明显，且对降雨的响应出现滞后效应[24]。经模拟结果与实测结果对比，深埋深条件下含水率的平均均方根误差（RMSE）和决定系数（R2）分别是0.012，0.91，浅埋深条件的对应值分别是0.013，0.96，温度误差在3 ℃以内，实测值和模拟值吻合度较好，可用于实际模拟应用。

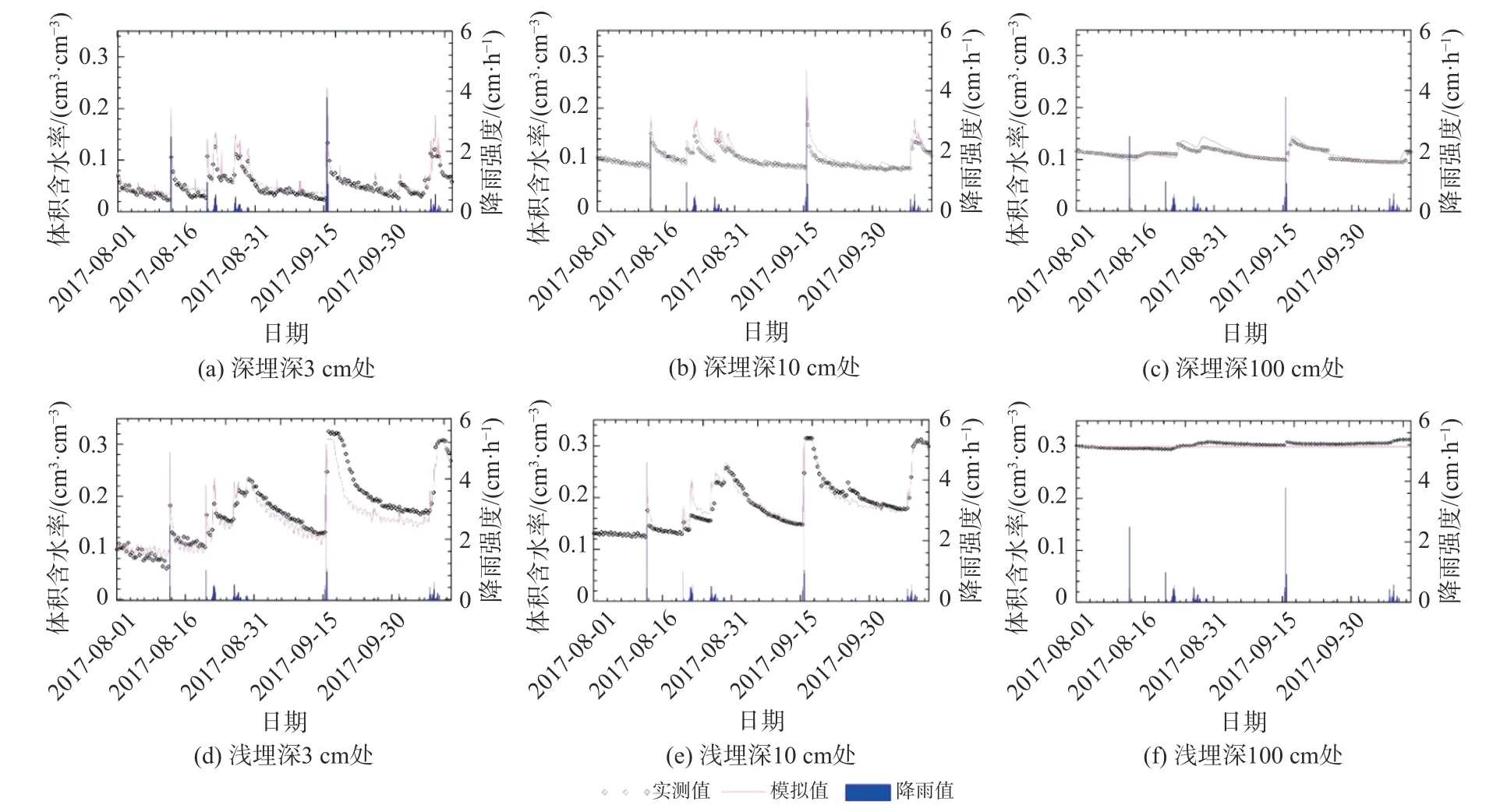
图2 土壤含水率实测值和模拟值随时间的变化Fig.2 Variations of the measured and simulated soil moisture

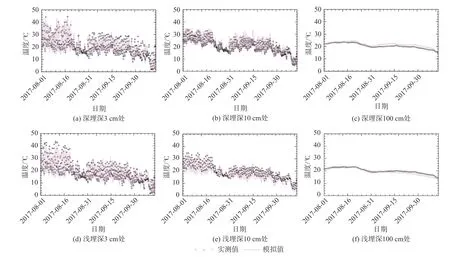
图3 土壤温度实测值和模拟值随时间的变化Fig.3 Variations of the measured and simulated soil temperature

3.2 不同地下水位埋深下土壤水的运移规律

水头是土壤水运动的主要驱动力，蒸发条件下当水位埋深较大时，包气带内存在随时间变化的零通量面，位于零通量面以上的水分向上运移[25]。由图4可知，地表以下0～100 cm土壤水头位于−300～−30 cm之间。降雨发生时，浅层的土壤水头迅速升高，伴随着降雨入渗，剖面深部土壤水头也逐渐升高，随着蒸发的持续，土壤剖面的水头呈逐渐降低的趋势，因此深埋深条件下，地下10～35 cm包气带存在一个随时间变化的零通量面；当降雨发生时，零通量面迅速抬升，接近地表；降雨结束后，零通量面逐渐回落。然而，对于浅水位埋深的土壤总水头，由于水位埋深很浅，包气带的水头值整体很高，剖面不存在零通量面。零通量面的存在使得土壤蒸发过程变得复杂，其位置直接影响着蒸发的强度和可持续性[7−8]。

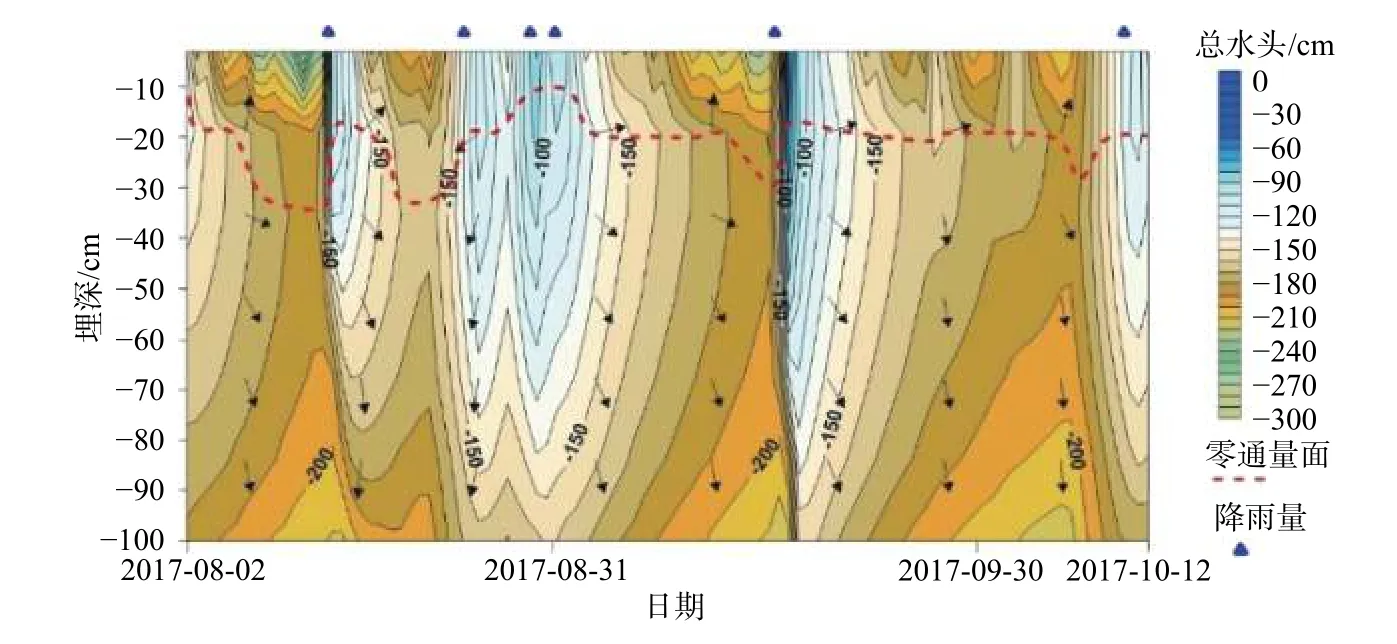
图4 深埋深条件下土壤水头的时空分布Fig.4 Spatial and temporal distribution of hydraulic head under deep buried condition

选择蒸发强烈的时段8月3—31日，通过模拟结果对比分析，图5为两种水位埋深情景下土壤水的运移规律，虚线表示通量为零的面，其两侧的水分向相反方向运动，将虚线通常定义为干燥锋[17]。由于深埋深剖面60 cm以深土壤水均向下运移，因此仅选择地下0～60 cm以内的土壤水通量。从图5可以看出，水位埋深对近地表土壤水的运动影响较大，蒸发条件下，发现在地表以下18 cm以浅，深埋深剖面存在孤立的干燥锋区域，同时，位于零通量面以下土壤深层（地下18 cm以深）出现连续的干燥锋，干燥锋的出现改变了土壤水的运动方向，阻断了土壤水向上运移；然而，与深埋深情景相比，浅埋深剖面土壤水均向上运移，当到达地表时开始蒸发。

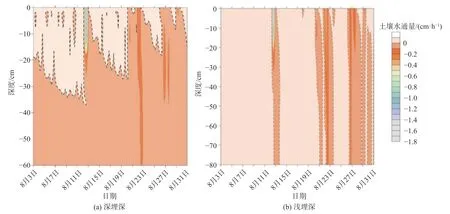
图5 土壤水通量时空分布图Fig.5 Spatial and temporal distribution of soil water flux

3.3 土壤剖面水头与温度梯度的分布特征

水分在土壤内的运移受水头梯度和温度梯度的共同驱动，为了分析驱动力对土壤水运移的影响机制，两种水位埋深情景下剖面水头梯度和温度梯度分布如图6所示，从整体上看，受太阳辐射的影响，近地表处包气带水头和温度梯度变化很大，呈稀疏和密集交替的变化趋势。

对于深埋深情景，蒸发条件下，位于零通量面以上的近地表区域出现孤立的干燥锋区域，见图5（a），此时该区域内水分受正水头梯度驱动作用向上运移，然而浅层包气带水分含量很低且热容较低，导致土壤剖面出现较大的负温度梯度，因此受正水头和负温度梯度的共同驱动，土壤水总体向下运移，见图6（a）、图6（b），说明水位埋深较大时，近地表范围的温度对水分运移过程起着重要的作用，改变了土壤水分仅受水头驱动时的运动方向，进而影响着土壤的蒸发过程；然而，位于零通量面以下的深层区域水分主要受负水头梯度驱动向下运移，这种现象与Zeng等[17]在室内观测与模拟得出的结果相似。对于浅埋深情景，蒸发条件下土壤剖面不存在孤立的干燥锋，水分以向上运移为主，受毛细上升力的作用，土壤整体含水率较高，相较于正水头梯度作用，负温度梯度对水分运移的影响很小，降雨发生时水分以向下运移为主，见图6（c）、图6（d）。上述现象表明不同水位埋深条件下土壤水表现出截然不同的水分运移过程，其中，水头和温度梯度决定着土壤水的运移方向。当水位埋深较大时，温度效应对水分运动起着重要的作用，而水位埋深较浅时，温度的影响可以忽略。

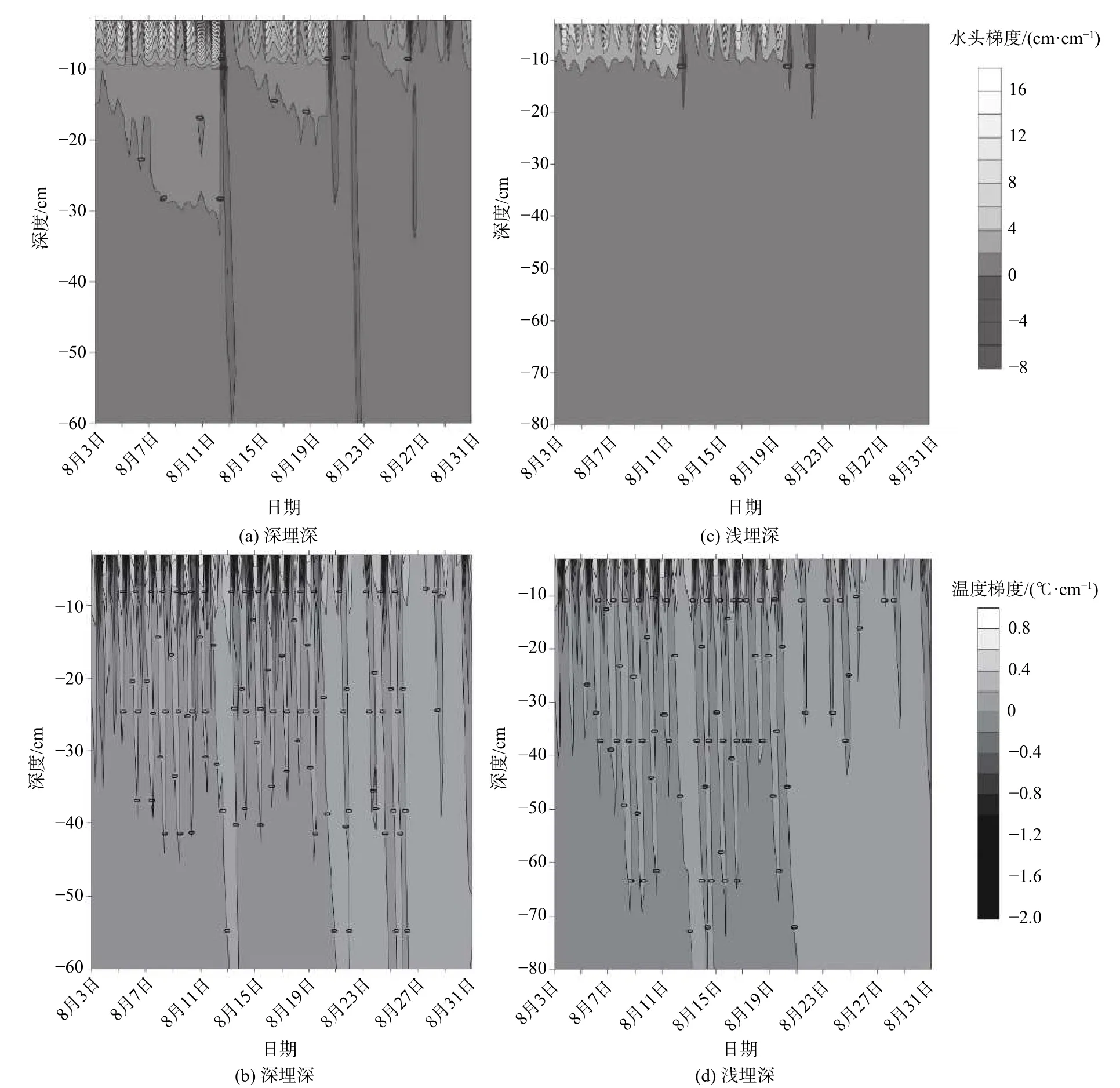
图6 土壤剖面水头和温度梯度时空分布图Fig.6 Spatial and temporal distribution of head and temperature gradients

3.4 水热运移对裸地蒸发的影响分析

深埋深条件下，土壤的累积蒸发量为4.1 cm；浅埋深条件下，为17.2 cm（图7）。浅埋深条件的累积蒸发量是深埋深的4倍多。量级差异主要是因为水位埋深不同时，土壤内部水热运移导致土壤水与地下水对蒸发贡献的输运机制不同，相比于深埋深条件，浅埋深水位更接近于土壤的毛细上升高度，地下水对土壤蒸发的贡献较大。

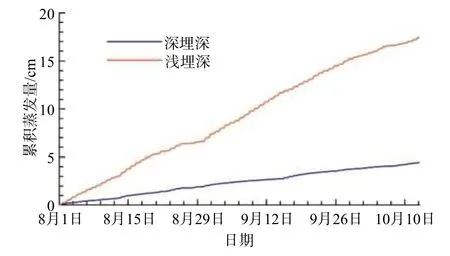
图7 不同水位埋深下土壤的累积蒸发量Fig.7 Cumulative evaporation under different depths of the water table

Lehmann等[26]利用砂质样品提出一个适用于细粒介质的蒸发特征长度bmax表达式，用于估计维持水力连接性的最大地下水位埋深：

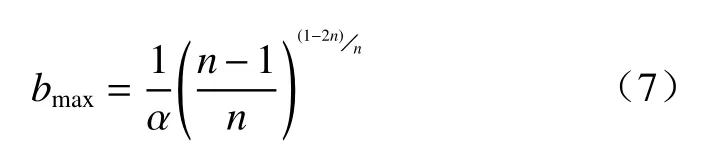
式中：α、n—van Genuchten模型的形状参数。

针对本次研究的风积沙介质，bmax计算值约为82.5 cm。试验监测期间，浅埋深水位小于蒸发特征长度，因此本研究中浅埋深对应的蒸发过程属于蒸发动力学第一阶段，土壤表面与地下水位或干燥锋之间存在连续的土壤水输运路径，即当地下水位埋深小于毛细上升高度时，包气带水与地下水存在强烈的水分交换，地下水受水头梯度驱动直接贡献土壤蒸发，正如Shokri等[27]通过室内研究指出，蒸发动力学第一阶段主要受毛细力的驱动作用。对于深埋深情景，地下水位埋深远大于土壤的蒸发特征长度，土壤蒸发进入动力学第二阶段，即当地下水位埋深大于毛细上升高度的1.6倍时，地下水不再直接贡献土壤蒸发，此时温度在土壤蒸发过程中扮演着重要作用，影响了土壤水的相态转变，包气带内部干燥锋区域的出现使得地下水与包气带水的水力连接断开，阻止了土壤水的向上运移。进一步证实水热运移是影响土壤蒸发动力学过程的关键因素。

4 结论

（1）本文以半干旱地区毛乌素沙漠为研究区，立足原位监测和数值模拟，将土壤-包气带-地下水看作一个整合的系统，揭示了土壤内部复杂的水热迁移转化，发现不同水位埋深条件下，土壤内部的水分分布规律明显不同，这是因为土壤水运动受不同水热耦合作用的控制，剖面不同深度的水头和温度梯度共同驱动着土壤水的运移方向和分布特征。

（2）在深埋深情况下，地下水位埋深大于毛细上升高度，地表以下10～35 cm深度出现随时间变化的零通量面，位于零通量面以上的土壤水向上运移参与蒸发；受近地表负温度梯度的影响，土壤剖面产生相互孤立的干燥锋，阻断了水分向上运移，进而抑制了土壤蒸发，温度效应在土壤水运动中扮演着重要角色。

（3）当地下水位埋深小于毛细上升高度时，地下水与包气带水之间具有较高的水力连接性，地下水在毛细力驱动下直接贡献蒸发，温度对水分运动的影响可以忽略。

（4）不同水位埋深条件下，土壤水的运移过程在水热耦合的控制下处于不同的蒸发动力学阶段，研究进一步表明，当水位埋深大于毛细上升高度的1.6倍时，地下水不再直接参与土壤蒸发，研究结果为解决半干旱地区无效蒸发等关键问题提供了参考。