井内嵌入同轴多孔与固体圆柱地下水渗流流型分析
2021-07-23雷海燕戴传山
朱 琳,雷海燕,马 非,戴传山
(天津大学中低温热能高效利用教育部重点实验室,天津 300350)
垂直于圆管外的绕流现象是自然界较普遍存在的流体力学现象之一,如卡门涡街。在多孔介质渗流层内垂直于圆管外的绕流问题也是石油钻探、地下水开采[1]、地热能开发、流化床等许多工业领域经常遇到的物理现象,如地热井筒与热储层的耦合传热问题[2],甚至在临床医学研究中也有相关的微血管外的间质渗流研究[3]。在饱和多孔介质内嵌入物体,被嵌物体外的绕流、传热传质问题在很多工业应用领域中有广泛的应用。针对多孔介质内嵌有简单几何形状的物体结构,若能获得其物体外部的绕流与热质扩散的问题的简单表达形式的理论解析解,对指导类似结构下的工业设计有重要的作用。
Pop等[4]首次获得了考虑流体黏性耗散Brinkman模型圆柱外绕流的理论解析解。相对Pop等[4]研究的有渗流通过的多孔介质内嵌入圆柱的流场结构而言,多孔介质内开挖有一圆形孔洞,且孔洞内充满纯流体的空间结构下的流场理论解析解获得的比较早。Drost等[5]采用忽略惯性力仅考虑流体黏性力的Stokes流模型获得了无限大多孔介质内有一圆形孔洞的流场理论解析解,得出孔内平均流速与地层远端流速相比(即平均收敛因子)约等于2。Sano[6]进一步分析了圆形孔洞的存在对周围达西流的影响,得出在多孔介质渗透系数较低情况下,孔洞圆心处速度约是远端地层渗流速度的3倍等重要结论。这一结论随后得到了Momii等[7]在实验室内基于激光多普勒方法进行的实验验证。Raja等[8−10]进一步推导了有均匀渗流通过的不同渗透系数下多孔介质层内有一规则或微变形的圆形孔洞或球形孔洞结构下的流场内流体速度(即收敛因子α)分布理论解。
Li等[11]针对一种相对前人研究更为复杂的有渗流通过的无限大多孔介质内嵌一固体圆柱,且圆柱外包裹有水环的几何结构下的各区域流型结构进行了研究,其研究目的是获取多孔介质内嵌入细长吸收碳纤维捕捉流体内胶体颗粒物的机理。Sekhar[12]将流体环内固体替换为多孔介质,得出该几何结构下的流动问题理论解,分析了内、外多孔介质在不同渗流系数情况下,整体多孔介质表现出的宏观平均水文特征、局部速度分布以及流动阻力特性。
前人研究结果表明,有均匀渗流通过的多孔介质内嵌入固体圆柱、多孔层、有水环或无水环等复杂几何结构下流场的理论解析研究文献并不多见,应用领域或研究目的却比较广泛,如复合材料封井、井内流速观测[13]、控制污染物在地下水和土壤中的扩散[14]等。值得注意的是,前人最多只对3层结构,即无限大多孔介质-水环-环状多孔层/圆形固体进行了研究。本文借鉴以往的研究方法,对有渗流通过的无限大多孔介质流场内嵌入固体圆柱,且圆柱外部顺序包裹有多孔介质环、纯流体环的复杂几何结构下的流场速度解析解进行了理论分析,着重研究了不同渗透系数下的内外多孔介质、水环间隙情况等对圆柱外绕流流型以及纵横界面上的速度分布的影响规律。由于地下水渗流速度较小,以往研究中常不考虑由弥散效应引起的黏度系数的变化,即多孔介质内黏度系数与纯流体内的黏度系数视为相同[15]。此外,在井筒附近的地下水渗流可能会产生颗粒的沉积堵塞[16],但本研究忽略这一影响,认为局部渗透系数不变。本文研究结果对类似结构下的地埋管套管换热器、地下水污染物吸收装置设计、地下水测速装置研发等有一定的理论指导意义。
1 物理模型的建立与求解方法
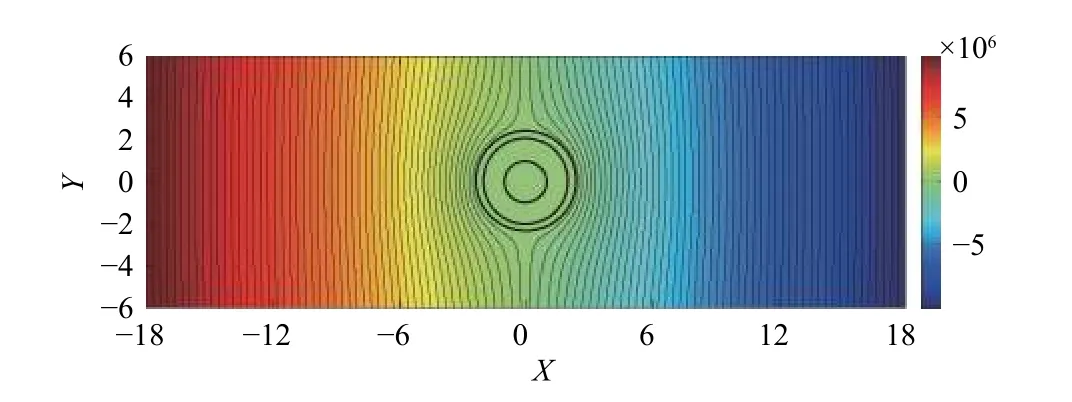
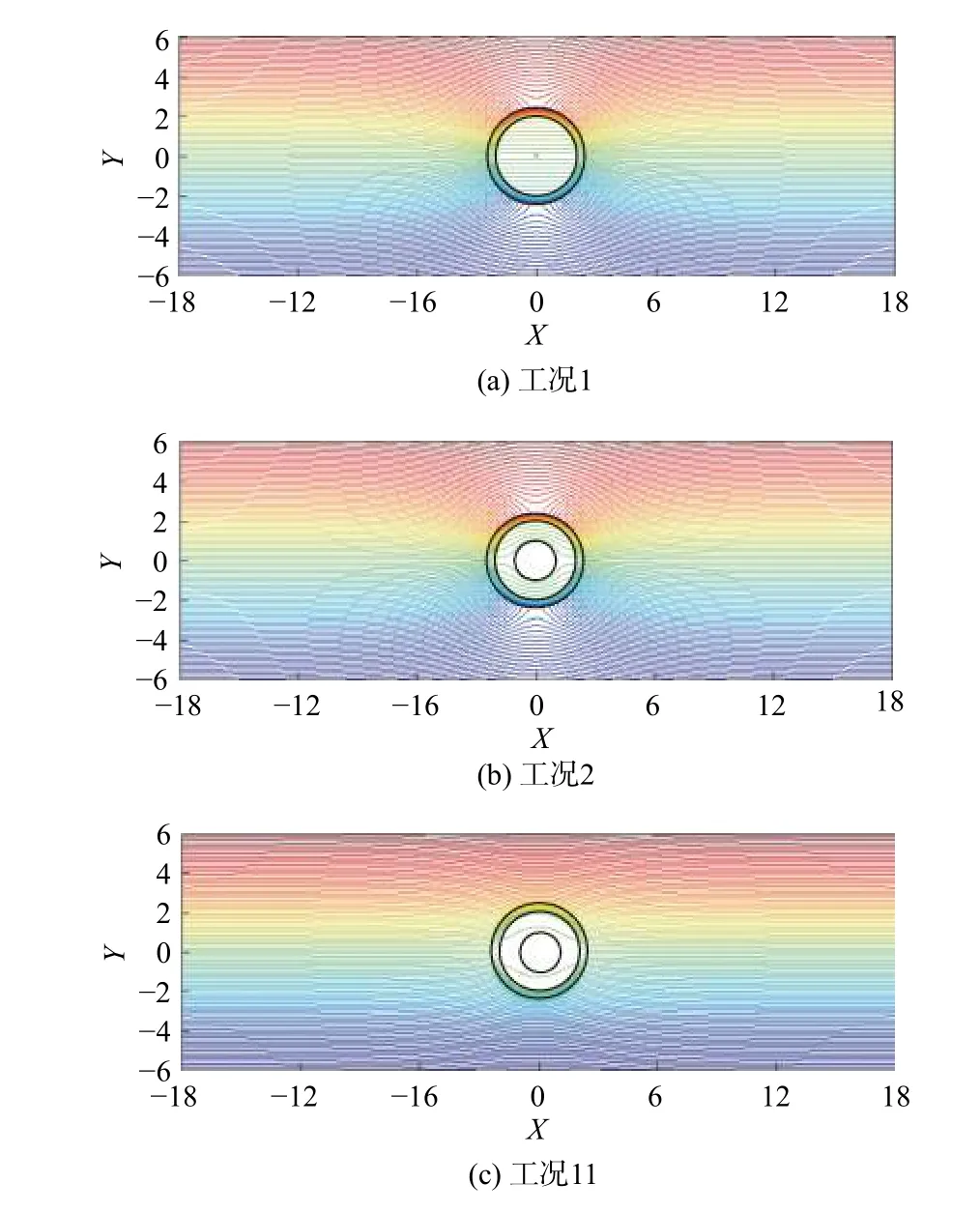
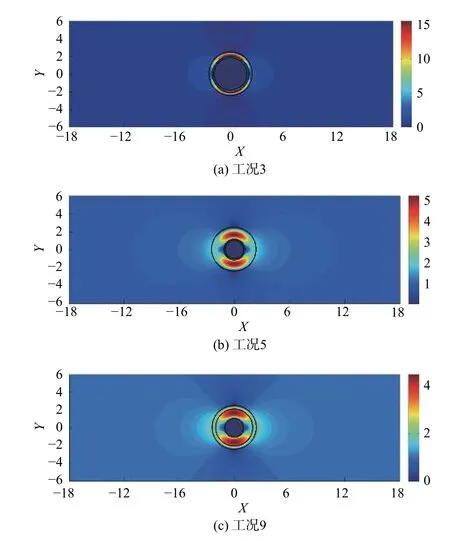
考虑无限大2D均质多孔介质(Pe)内有单向渗流,垂直井筒内另嵌入同轴均质多孔介质(Pi)与固体圆柱(S),在内外多孔介质之间有开放水环(Wen)的情况,假设多孔介质均为各向同性材料:渗透系数为ke的无限大多孔介质内有黏性流体稳定通过,绕过井中一包裹有渗透系数为ki的多孔层且半径为r0的圆形固体(图1)。水环区域(λ1r0 图1 物理模型示意图Fig.1 Schematic diagram of the physical model. 水环内、外多孔介质区由Brinkman方程[18]和连续性方程控制: 式中:µeあ—多孔介质内流体有效黏度系数; µen—水环内纯流体黏度系数,µeあ=µen=µ; en—水环; l=i、e—内部、外无限大多孔介质区。 速度矢量(V)、横纵坐标(x、y)、各点到固体圆柱圆心半径(r)和压力(P),进行无量纲化: 式中:U∞—无限远处的流速大小。 水环区控制式(1)(2)无量纲化: 多孔区控制式(3)~(4)无量纲化: 式中:χ2—渗透性能,χ2=r20/k。 由速度分量和剪切应力(T)的连续性[19−20],得到边界条件(每个边界条件都可以分解为切向和法向,切向剪切应力包含压力P): 引入极坐标系下的流函数(ψ): 式中:θ—速度分量Vθ与横坐标轴x夹角。 式(6)—(8)简化为: 结合无穷远处均匀流动条件ψe∞→−rsinθ,各区域式(13)(14)的解为: 式中:I1—第一类修正一阶贝塞尔函数; K1—第二类修正一阶贝塞尔函数。 其中系数A、B、C、D、E、F、G、H、M、N可由式(9)—(11)确定。 值得注意的是,若r0→0,解的形式与Sekhar[12]一致: 此外,若r0→0,λ1→0,解的形式为: 笛卡尔坐标系下的流速U: 为了验证计算方法的正确性,本文以Raja等[8]的计算模型为例,进行了程序正确性验证,该模型中包括纯流体孔洞部分的Stokes流模型以及外部多孔介质部分流动的Brinkman模型。输入参数与文献[8]一致,结果见图2。 图2 χe变化下纵向中心剖面(Y=0),横向中心剖面(X=0)无量纲速度分布图Fig.2 Dimensionless velocity distribution map of the longitudinal center profile(Y=0) and the lateral center profile(X=0) under the changes of χe 该计算模型对应于无限大多孔介质内有一孔洞的情况,即r0→0,λ1→0。其中,横纵坐标无量纲化:χe变化下经过圆心的纵、横剖面速度分布见图2。值得注意的是,无量纲化特征长度为孔洞半径r0c=λ2r0。随着χe的增加(渗透系数变小),孔洞的存在感变强,中心流速与远端流速比值αc变大到3,若χe为0(渗透系数极大),则αc→1。本文结果与Raja等[8]研究结果符合非常好。 在方法验证的基础上,对图1所示的多层结构模型进行理论求解。由于影响参数比较多,仅对不同半径、以及内外渗透系数变化情况下的流型结构求解。计算工况见表1。值得注意的是,为了更清晰地表示外部尺寸固定(即λ1/λ2为定值)情况下,内部圆柱尺寸的变化对于流场的影响,此处给出的r0是一组以r0=r02为标准的假设值(流场的变化只与λ1、λ2、χi、χe有关)。同理,整个流场均如式(5)所述,计算过程中使用相应的r0进行参数的无量纲化为了更加直观地看出不同参数的影响,在计算结果的整理中,横纵中心剖面坐标轴的无量纲化均以r02半径为准: 表1 不同工况的计算参数Table 1 Summary of calculation conditions under different parameters. 图3(a)(b)可以看出,固体半径r0的变化对水环外的多孔区几乎没有影响。但随着r0增大,水环内流速峰值变高,这是由于流体经过包裹有多孔层的固体结构时流动阻力变大(图4)。此外,r0变大,固体圆柱在多孔介质层中对流体的影响半径增大,逐渐呈绕流趋势,如图5(a)(b)。更进一步地,水环内的多孔区纵向剖面的平均流速值变小,横向剖面上的速度变大。这是因为该区域内部阻力变大,流入的流量越来越少,但绕流增加了横向剖面上的流速。另外,在r0极大的情况下(工况3),多孔层内流速急速下降到0,这是由于极薄多孔层对流场没有太大影响,如图6(a)。 图3 纵向、横向中心剖面无量纲速度分布图Fig.3 Dimensionless velocity distribution map of the longitudinal center profile and the lateral center profile 图4 典型工况下的压力云图(工况2)Fig.4 Pressure contours under typical working condition 2 图5 典型工况下的流线图Fig.5 Streamline diagram under the typical working conditions 以工况2为对比工况,分别研究参数λ1、λ2、χi、χe的变化对流型结构的影响。此外,由于绕流,流体在水环内横向剖面上的流速变化更为明显,因此水环内 流型变化主要用该剖面上的流速峰值分析。 图3(c)(d)为λ1变化下的中心剖面无量纲速度分布图。λ1的变化对水环外的多孔区(下文简称外多孔区)几乎没有影响。但是,随着λ1变小,水环内流速峰值先变高后变低,这是由于缝隙变大,进而剖面上速度分布展宽变大。即进入水环内多孔区(下文简称内多孔区)的流体变少,而水环内流量增加流速变大,直至流体几乎不通过内多孔区(工况5),见图6(b),且过程中随着展宽变大,水环内流量分配空间变大导致其流速峰值逐渐降低。类似地,由于缝隙变大,内多孔区阻力相对水环阻力变大,该区域流量降低流速变小,因此流场也更容易平稳。同时,λ1的减小会使内多孔层中的绕流效果相对增强,因此该区域流型平稳程度要耦合区域内流量大小和圆柱外绕流强度两种因素。 图6 典型工况下的速度云图Fig.6 Speed contours under the typical working conditions 图3(e)(f)为λ2变化下的中心剖面无量纲速度分布图。当λ2很大时,缝隙很大,极少流体流入内多孔区(工况6)。随着λ2的增大,水环内流速峰值先升高后降低,这是由于缝隙变大流速分布展宽变大,流体越来越少地进入内多孔层且水环内流量分配空间变大导致的。由于内多孔区阻力相对水环阻力增大,该区域平均流速成倍降低且流型变化趋势更平稳。λ2减小,意味着整个障碍物尺寸相对减小,因此,外部多孔介质区的流型会更加平缓。 图3(g)(h)为χi变化下的中心剖面无量纲速度分布图。χi的变化对外多孔区的流场几乎没有影响。但是,当χi极大时,流体几乎不进入内多孔区。随着χi的减小,水环内流速峰值降低。这是因为内多孔区渗透性加强,内多孔层阻力相对水环阻力变小,内多孔区流量变大水环内流量减小。同理,内多孔区横向和纵向剖面流速均相应变大,且变化明显。当内多孔区渗透系数极大时(工况9),见图6(c),水环与内多孔层之间的速度阶跃消失,出现“穿透”现象,这是因为内多孔层阻力与水环阻力同量级。 图3(i)(j)为χe变化下的中心剖面无量纲速度分布图。随着χe变小水环峰值降低,内多孔区流速越低流型越平缓,但外多孔区流速增大。这是由于内外多孔区渗透系数差变小,整体结构流型过渡更为平缓,水环内的加速效应相应减弱,内多孔区的流速相应降低。χe≤10时外多孔区流速变化趋势与χe较大时相反,这是由于与流体向水环内的渗透作用相比,水环外的绕流作用占了主导地位,见图5(c),流体极少进入内多孔区。 (1)水环内部参数如r0、λ1、χi的变化对外层多孔介质区影响很小;水环直径的减小会使外部流型更为平稳;水环外部流型主要受控于外部渗透系数,但由于障碍物的存在,渗透系数对外部流型的影响是非单调的函数。 (2)横向剖面上水环内的速度变化较大,固体圆柱r0减小,水环内峰值增加。内部与外部渗透系数同时增大,水环内加速效应减弱。水环间隙对水环内流速峰值影响较大。 (3)研究发现内部渗透系数增加到某一临界值情况下会出现“穿透”现象,横向速度剖面从阶梯形变为抛物线形。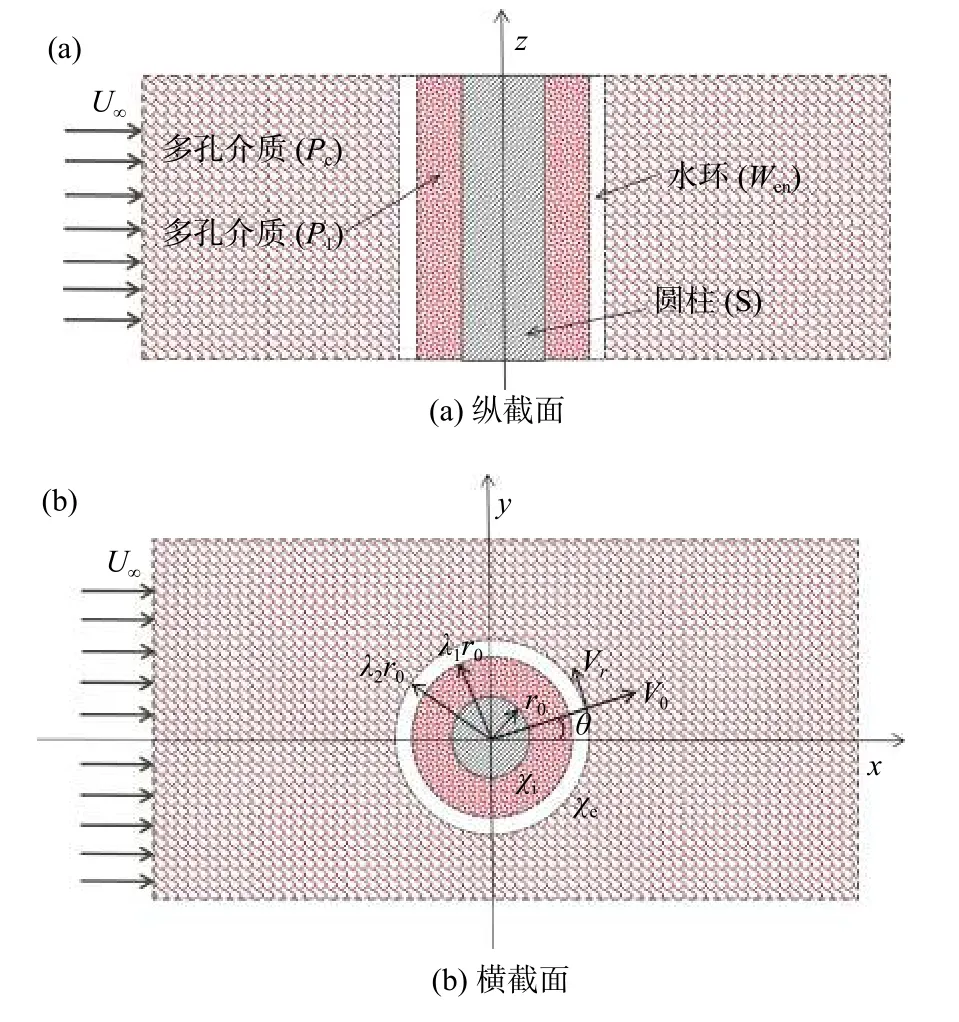


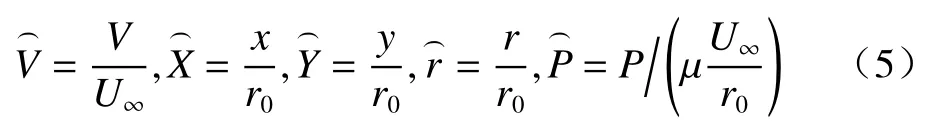


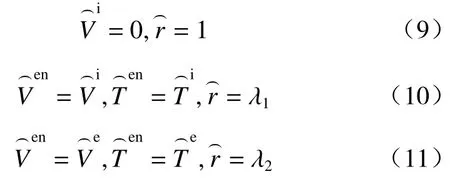
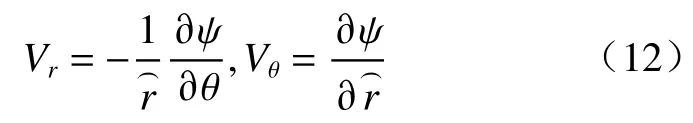

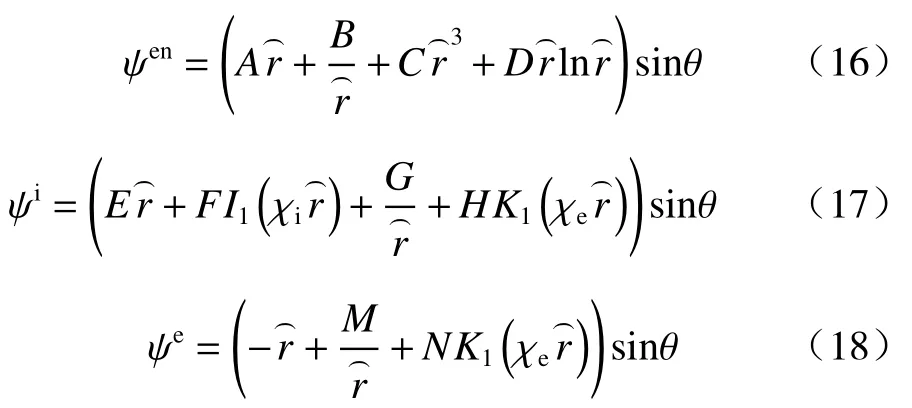
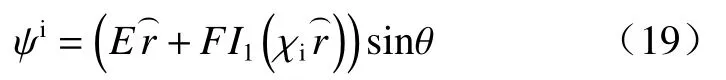
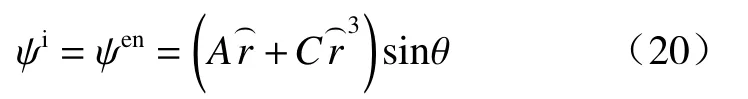

2 方法验证

3 多层结构计算结果

3.1 固体圆柱半径大小r0对流型结构的影响

3.2 λ1变化对流型结构的影响
3.3 λ2变化对流型结构的影响
3.4 χi变化对流型结构的影响
3.5 χe变化对流型结构的影响
4 结论
