考虑路面不平顺随机性的汽车过桥动力响应分析

谢娟娟， 李 晋， 田 震， 甄龙信， 谷 雨， 劳晓东， 张成光

(1. 周口师范学院 机械与电气工程学院，河南 周口 466000; 2.燕山大学 车辆与能源学院，河北 秦皇岛 066000)

随着城市的发展以及人们对出行效率的追求，各大城市早已开始规划起高架桥交通路线，不仅能提高利用空间，还能够实现市内快速交通，提高城市效率。由于公路路面施工、损坏及温度变形等原因，会对路面平顺性造成不同程度的影响，因此需要对路面的平顺性进行分级。在城市快速公路上，由于车速较快，对路面的平顺性要求较高，当车辆通过桥梁时，会对桥梁产生冲击荷载[1]，桥梁的动力响应与路面的平顺性会影响车辆的运行舒适性[2-3]，此时路面的不平顺相当于1个外部激励施加于车辆与桥梁系统上，而路面不平顺是1个随机过程，因此整个车辆-桥梁系统是1个随机系统，需要建立随机车桥耦合数学模型从概率的角度对车辆的响应进行分析。

车桥耦合振动研究已经开展了数十年，Fryba等[4]、Yang等[5]、雷晓燕等[6-7]以及夏禾等[8]从移动荷载解析解到车桥耦合数值解均作了详细的研究，取得了大量研究成果，在这些研究中，主要针对列车轨道桥梁系统。王贵春等[9]通过ANSYS有限元软件建立了车桥耦合振动模型，并基于福建长门大桥进行了不同车速及载质量的行车舒适性分析。韩万水等[10]将风、汽车、桥梁三者作为1个相互作用的系统，提出1个的风-汽车-桥梁系统空间耦合振动分析模型。胡昌斌等[11]路面板固化翘曲对车辆行驶舒适性的影响。

以上研究中，针对的是确定性车桥模型，为探讨车辆、结构参数及路面不平顺随机下的车桥系统振动，桂水荣等[12]将车辆简化为两自由度系统，并基于虚拟激励法分析了随机车桥振动，讨论了不同车速下随机响应的变化情况。Wu等[13-14]通过混沌多项式及KL展开法将桥梁处理为随机有限元，并将路面不平顺通过KL展开形式表达，进行了包括车辆荷载识别、路面不平顺程度对随机车桥系统的影响，桥梁变异性的影响等较为系统的研究。余志武等[15-16]采用概率密度演化方法对随机列车-桥梁系统进行了研究。概率密度演化方法最早由李杰等[17]提出，该方法是1个高效、精确的随机系统、可靠度分析方法，目前该方法已广泛应用于考虑结构参数或车辆参数随机的随机振动分析以及考虑地震激励、轨道不平顺激励等随机振动中。本文将基于概率密度演化方法，探讨其在考虑道路不平顺随机性的汽车-桥梁耦合振动分析中的可行性，并从概率的角度分析路(桥)面不平顺性对车辆动力响应的影响，从而为汽车过桥时的随机动力响应、平稳性分析或桥梁随机结构动力、疲劳响应分析提供理论依据。

1 汽车-桥梁耦合振动模型

1.1 车辆运动方程

一辆汽车以匀速运动在1个简支梁上行驶，如图1所示，其中车辆模型为1个质量-弹簧-阻尼体系，包含1个车体、2个轮轴和2个轮对，车体包含垂向位移和点头2个自由度，每个轮轴各有1个自由度，假设轮对与桥面密贴，因此，轮对无独立自由度，则整个车辆体系共有4个自由度。根据拉格朗日方程可以得到车辆的动力学方程为

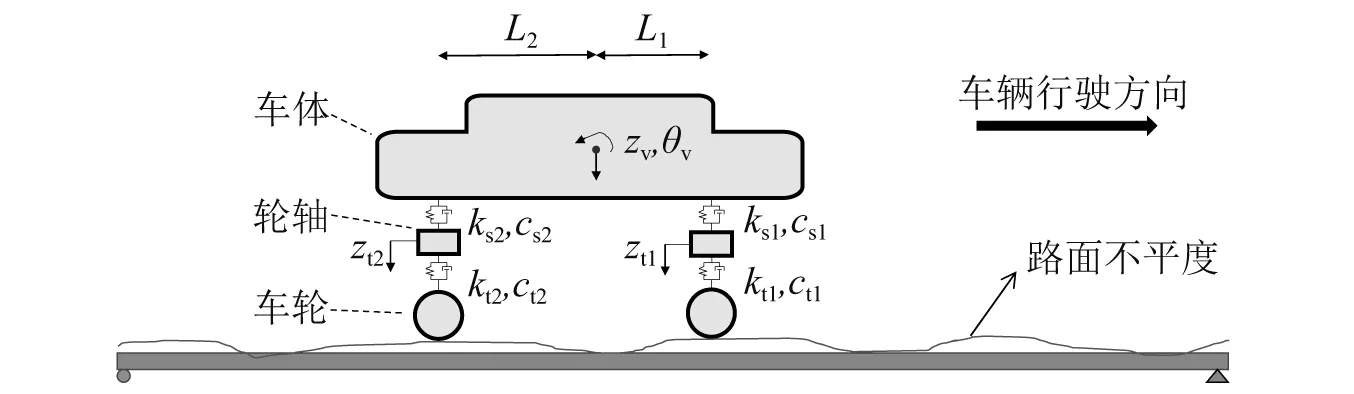
图1 汽车-桥梁模型

(1)

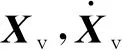
Mv为车辆的质量矩阵，可以表示为

Mv=diag[mv,Iv,mt1,mt2]

(2)

式中：mv和Iv分别为车体的质量和转动惯量;mt1和mt2分别为前、后轮轴的质量。

Kv为车辆刚度矩阵，可以表示为

(3)

式中:ks1和ks2分别为车体与前、后轮轴悬挂弹簧的刚度；L1和L2分别为车体重心到前、后轮轴的距离。

Cv为车辆阻尼矩阵，可以表示为

(4)

式中，cs1和cs2分别为车体与前、后轮轴悬挂弹簧的阻尼系数。

Fv为车辆荷载列阵，主要由车辆自身的重力以及轮轴与车轮间的悬挂弹簧力组成，可以表示为

(5)

(6)

(7)

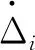
Δi=zti-zbi-zrou,i

(8)

式中：zti为第i个轮轴的垂向位移；zbi和zrou,i分别第i个轮轴位置处的桥梁垂向位移和路面不平顺。

1.2 桥梁运动方程

桥梁采用单跨简支欧拉-伯努利梁进行模拟。采用有限元方法建立桥梁模型，其中，每个结点包含垂向位移和转角2个自由度，将梁单元刚度进行组装得到总体刚度矩阵，随后可以得到桥梁的运动方程

(9)

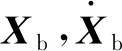
(10)

式中，Nb1和Nb2分别为前、后轮轴架构弹簧在桥梁上对应的插值形函数。

1.3 车桥耦合系统动力方程

将式(1)与式(9)联立，得到车桥耦合系统的动力学方程为

(11)

在得到系统动力学方程后，可以采用时程逐步积分法进行求解，由式(8)可知，式(11)中的荷载列阵为隐式函数，无法直接采用隐式积分进行求解，因此需要进行迭代求解。采用Newmark-β积分对式(11)进行迭代求解，迭代的收敛条件采用文献[19]中介绍的交叉迭代算法。

2 概率密度演化的随机振动理论

2.1 路面不平度模拟

路面不平顺是1个随机过程，根据Wu等的研究，路面不平顺是1个零均值的高斯随机过程，其中路面不平度功率谱可以表示为

Gq(n)=Gq(n0)(n/n0)-w

(12)

式中：Gq(n0)为道路不平度系数，根据道路不平度等级进行确定;n0=0.1 m-1，w为频率指数，一般取值为2;n为空间频率。

可以通过快速傅里叶变换将路面谱进行模拟，如式(13)所示

式中：Lc为路面不平顺长度，在本文中取3倍的桥上跨(进桥前，桥上，出桥后各1倍桥跨长度)；θk为一组独立的服从[0, 2π]的均匀分布随机变量。

2.2 概率密度演化方法

概率密度演化最早由李杰等提出，在余志武等研究中首次将该方法运用于考虑轨道不平度的列车桥耦合随机振动。在本文中，仅考虑路面不平顺随机。将式(11)写成一般动力学方程形式有

(14)

式中，Θ为基本随机变量参数。

则式(14)得到的解是存在、唯一且连续地依赖于随机参数Θ，为方便描述，将式(14)得到的解写成以下形式

X=H(Θ,t)

(15)

在X中包含多个响应量，如桥梁的位移、加速度以及车辆的位移、加速度等。将所需要分析的m个响应量记为Z=(Z1,Z2,…，Zm)T，将其表示为基本随机变量的函数有

(16)

式中，hz(Θ,t)=∂Hz(Θ,t)/∂t。

由于没有其他随机源，且已有的随机因素未消失，则车桥耦合系统能够满足概率守恒条件，根据李杰等的研究有

(17)

式中，pzΘ(z,θ,t)为联合概率密度函数。

由Reynold转换定理，结合式(16)和式(17)经过一系列数学变换即可得到广义概率密度演化方程

(18)

在实际计算中，可以依次计算单个需要的物理量从而简化计算，则式(18)退化为以下一维方程

(19)

式(19)的初始条件为

pzΘ(z,θ,t0)=δ(z-z0)Pq

(20)

式中：z0为确定性初始值; δ为狄克拉函数;Pq为附得概率。

概率密度函数随时的演化为

(21)

式中，npt为计算样本数量，在得到各个时间点响应的概率密度函数后，即可方便得到对应的均值、标准差等统计量。

考虑路面不平顺随机性的车辆-桥梁耦合振动的概率密度演化计算流程，如图2所示。

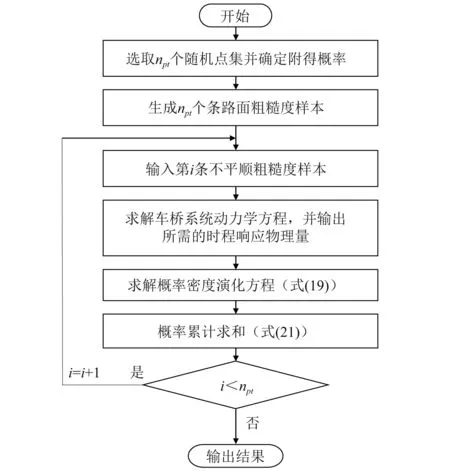
图2 计算流程图

3 方法验证

3.1 车桥系统验证

为验证车辆-桥梁耦合动力系统的可靠性，将计算结果与经典算例中的计算结果进行对比验证。在该算例中，有一辆两悬架汽车以20 m/s的车速经过一跨简支梁，桥梁的具体参数如表1所示，车辆的具体参数如表2所示。由于路面不平顺具有随机性，因此得到的响应结果也具有随机性，然而，由文献[20]可以知道，路面不平顺是1个零均值高斯随机过程，因此耦合系统响应的均值可以认为是零路面不平顺情况下得到的系统响应，因此可以将Wu等研究中均值响应结果与本文中不含路面不平度的结果进行对比。图3为本文计算得到的桥梁跨中位置竖向位移的时程曲线与经典算例的对比结果，可以看到，本文计算结果的趋势与经典算例的结果基本一致，最大挠度值略大于经典算例，但仍在可以接受范围内，因此可以认为本文的车辆-桥梁耦合系统振动是可靠的。

表1 桥梁参数

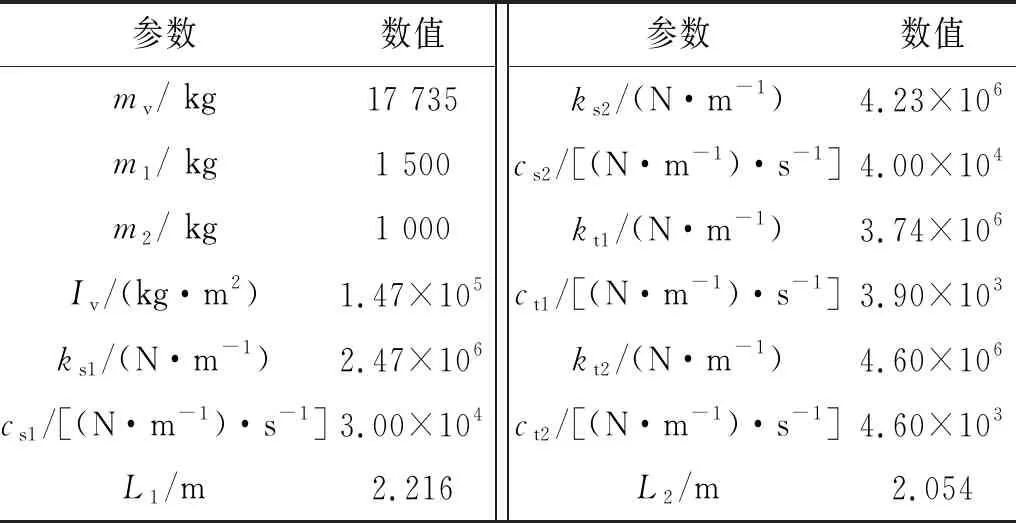
表2 车辆参数

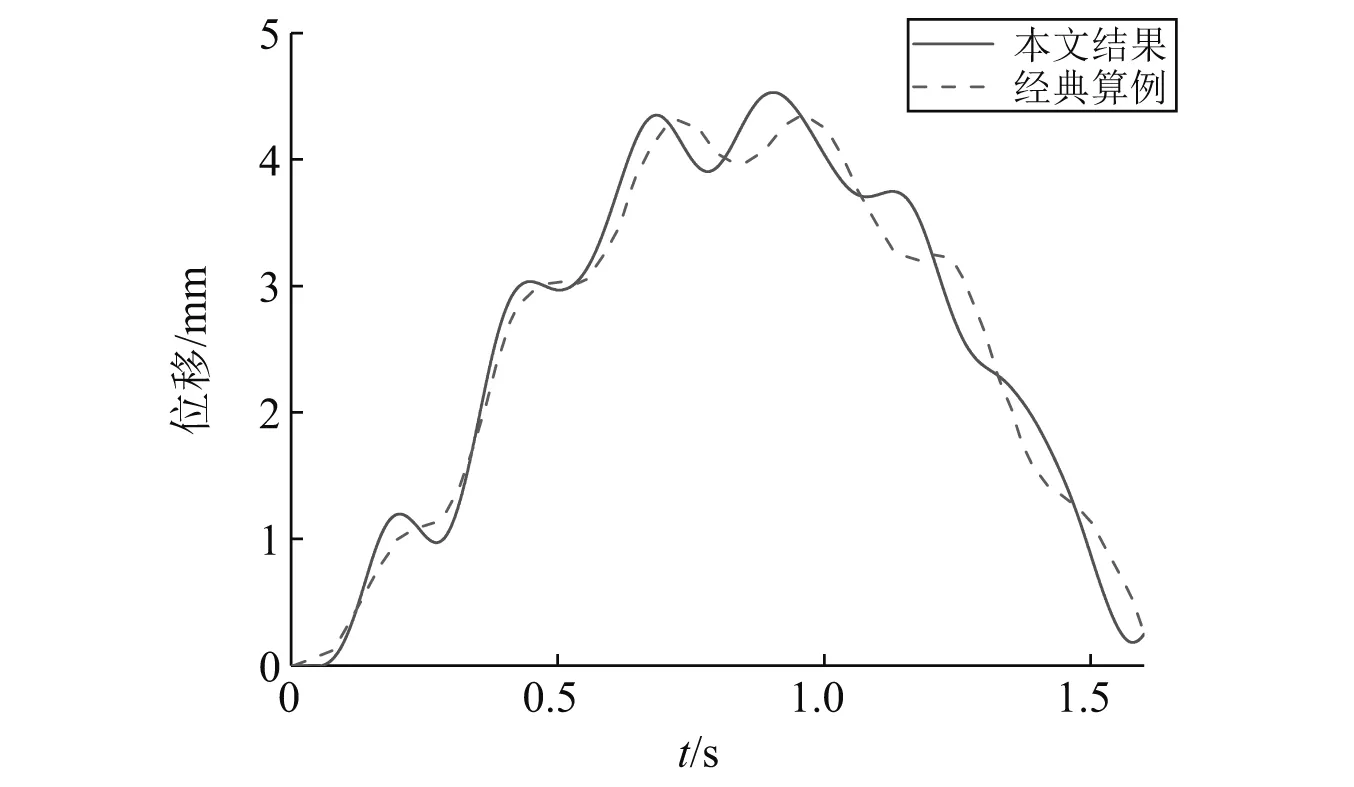
图3 桥梁跨中挠度对比

3.2 精度及效率验证

为探讨概率密度演化方法在车辆-桥梁随机振动中的适用性，将概率密度演化得到的车桥随机响应的结果与蒙特卡洛法(Monte Carlo simulation,MCS)进行对比，蒙特卡洛法是一种简单通用的随机分析方法，能够得到较为精确的解，但由于该方法需要大量的样本才能够达到稳定、准确的解，耗费过多时间，因此在工程分析中受到了一些限制。同样采用3.1节中的车辆及桥梁计算参数。桥上道路不平度为B级[21]，取路面不平度系数为0.64 mm2/m。蒙特卡洛法计算采用5 000条路面不平度样本，概率密度演化采用130条路面不平顺样本。图4为概率密度演化方法与蒙特卡洛法得到的桥梁跨中位置竖向位移时程曲线的均值及标准差的对比，可以看出在车辆刚进入桥梁时桥梁随机响应的变异性较小，随着车辆向前行驶，其变异性逐渐增大。此外，在桥梁响应均值方面，概率密度演化方法得到的结果几乎与蒙特卡洛法得到的结果重合，对于响应的标准差，概率密度演化方法得到的结果与蒙特卡洛法得到的结果非常接近，因此可以认为概率密度演化方法可以得到足够高的精度；蒙特卡洛法所采用的样本数量约为概率密度演化方法的38倍，概率密度演化方法的效率比蒙特卡洛法提高了1～2个数量级。

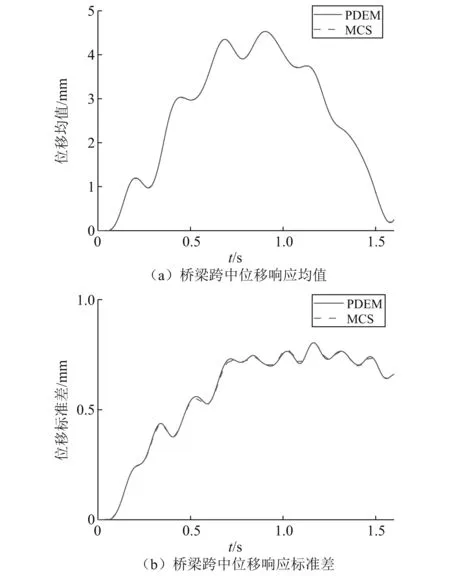
图4 随机响应对比

4 算例分析

由第3章中的内容可知，概率密度演化方法能够准确地计算车辆-桥梁耦合随机系统响应。为分析不同车速、不同道路不平度情况下的车辆随机响应，分别进行车速为5 m/s，15 m/s，25 m/s，35 m/s四种情况下的车辆-桥梁随机系统计算。两轴汽车是目前最为常用的汽车，在韩万水等、桂水荣等和Wu等的研究中均将该类型汽车作为研究对象进行讨论，因此本算例中车辆模型也选用两轴汽车，车辆与桥梁均采用第3章中的算例参数。道路不平度，即为不平顺的程度，根据GB/T 7031—2005《机械振动道路路面谱测量数据报告》，不同道路等级的不平度系数按均值取值，具体见表3。

表3 不平度系数

4.1 桥梁响应

图5为不平度B级、不同车速情况下车辆经过桥梁过程中桥梁跨中位移随机响应的时程曲线，其中横坐标为汽车前车轮驶过桥梁左边端点的距离。由图5(a)可以看出车速变化对桥梁均值响应没有明显影响；由图5(b)可以看出，车速在15 m/s和25 m/s情况下的桥梁响应接近，总体上桥梁响应标准差随车速增大而增大，且标准差的最大值出现的位置基本与均值最大值一致。高车速(35 m/s)工况下其桥梁响应标准差最大值较中速度(15 m/s)提高了68%。

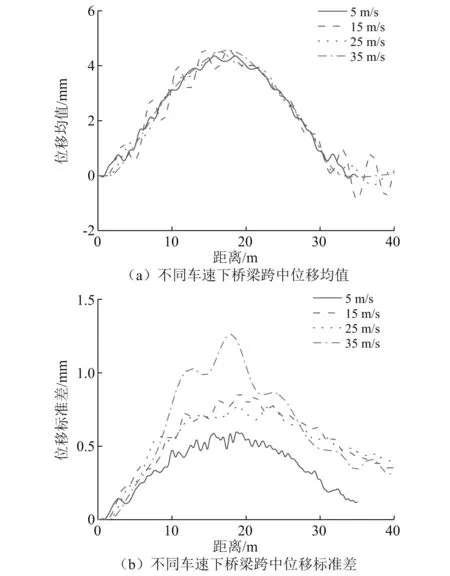
图5 桥梁响应与车速关系

在概率分布中，均值加减三倍的标准差基本涵盖了99.7%的概率值，为了分析不同道路不平度的路面不平顺随机激励下桥梁动力响应的概率最大值，采用均值加、减三倍标准差得到的响应最大值作为概率最大值。图6为不同路面等级情况下，不同车速通过桥梁时的跨中竖向位移概率最大值，可以发现，在不同道路等级工况下，位移概率最大值总体上都随车速增大而增大，在车速小于25 m/s时增长不明显，在车速大于25 m/s后增涨的幅值较大。在不同速度工况下，位移概率最大值随着道路不平度的加大而增大，道路等级为E即时，位移概率最大值相对于B级提高了216%～320%。

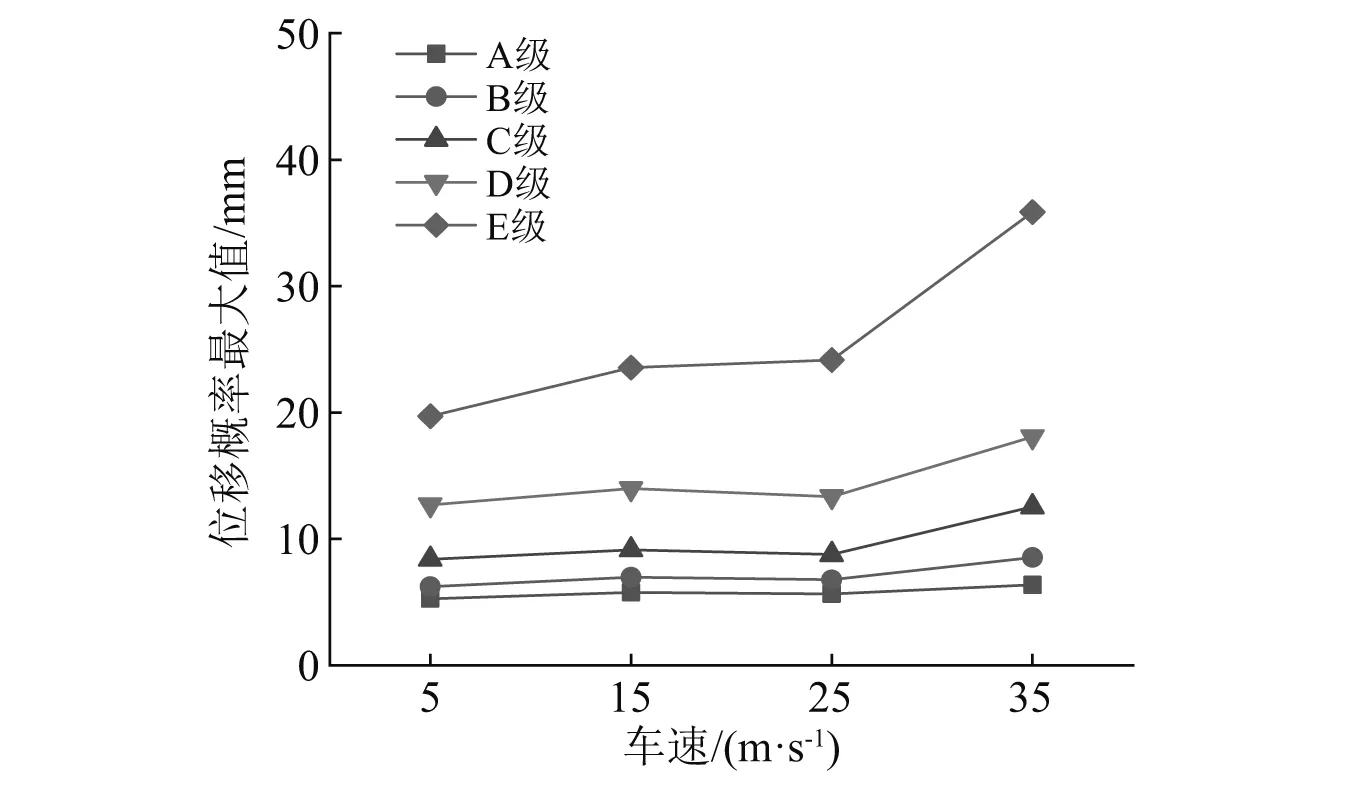
图6 桥梁跨中竖向位移概率最大值

4.2 车辆响应

图7为不平度B级、不同车速情况下车辆经过桥梁时的车体竖向位移响应的均值，其中横坐标为汽车前车轮驶过桥梁左边端点的距离。可以看出，汽车驶进桥梁的过程中，其竖向位移趋势为先增大后逐渐减小至零，其位移主要由桥梁的竖向变形引起。车辆的位移基本随着车速的增大而增大。此外，在低速(5 m/s)时，车辆位移响应震荡较为明显，在高速行驶(35 m/s)情况下，车体竖向位移响应明显增大，其最大值相较于其他车速增大了约24%。

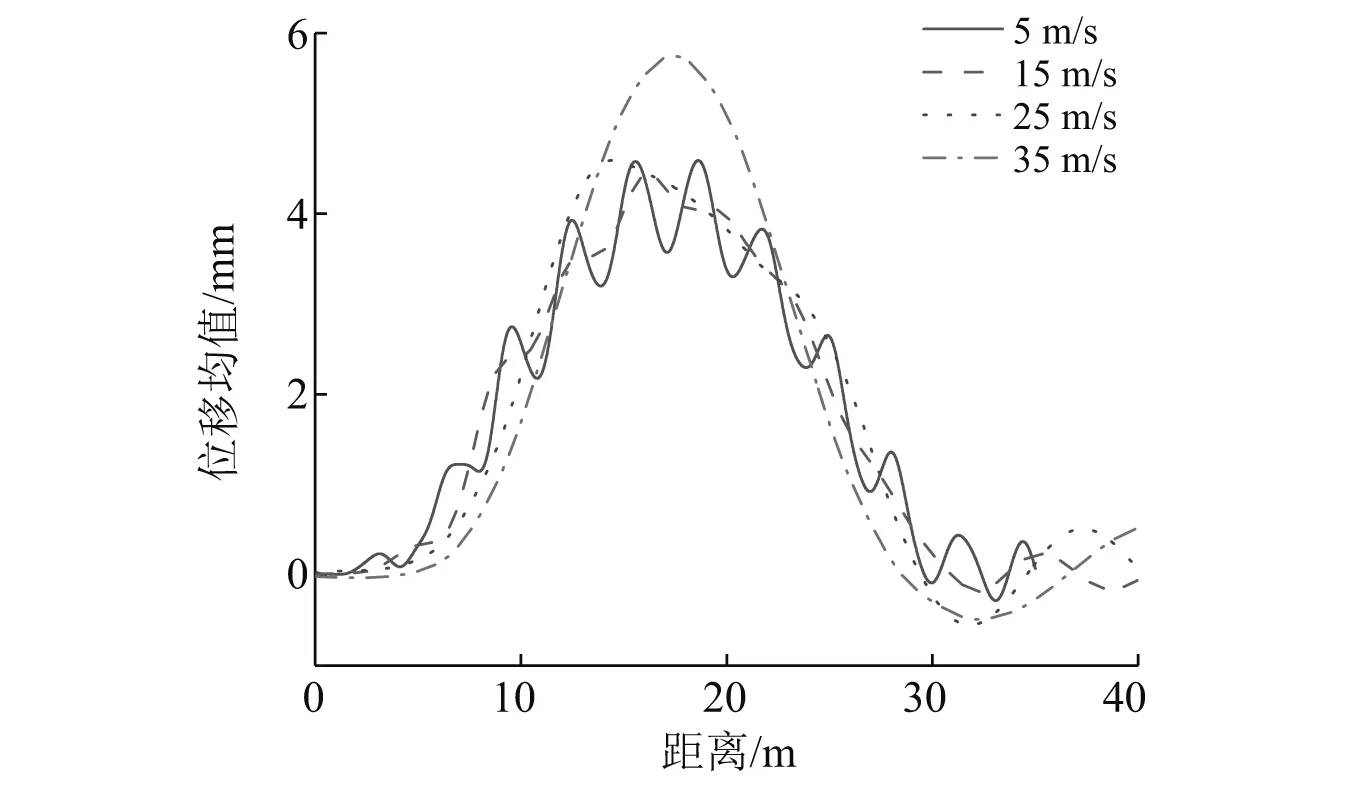
图7 车体竖向位移均值

图8为不平度B级、不同车速情况下列车经过桥梁时车体及悬架竖向位移的标准差最大值，可以看出车体位移的标准差基本随车速增大而增大，而悬架响应的最大值与车速没有明显关系，总体上看，悬架的竖向位移响应的标准差最大值与车体基本一致。

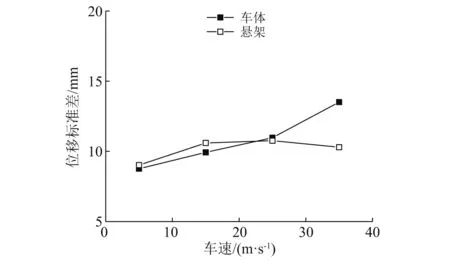
图8 车体、悬架竖向位移响应与车速关系

图9为不平度B级、不同车速情况下车辆经过桥梁时的车体竖向加速度均值时程响应，可以看出，车体加速度均值以零为中心进行震荡，车速越大，其震旦幅值越大，在车速超过25 m/s后，震旦幅值随车速增大明显增长。在高速行驶(35 m/s)情况下，车体振幅较大，且振幅频率减小。图10为不平度B级、车体与悬架标准差最大值随车速的变化情况，可以看出车体与悬架的标准差最大值均随着车速增大而增大，且悬架的增幅较车体大得多。总体上看，悬架的加速度标准差大于车体竖向加速度标准差。同时可以看出，车体竖向加速度均值响应基本沿着零进行小幅震荡，而其标准差大于其均值，这主要是由于路面不平顺为零均值随机过程，其均值响应接近无不平顺激励情况下的响应，其均值响应主要由桥面变形引起。悬架的竖向加速度响应的标准差较车体大，在高车速(35 m/s)情况下，悬架的竖向加速度标准差为车体的3.7倍。

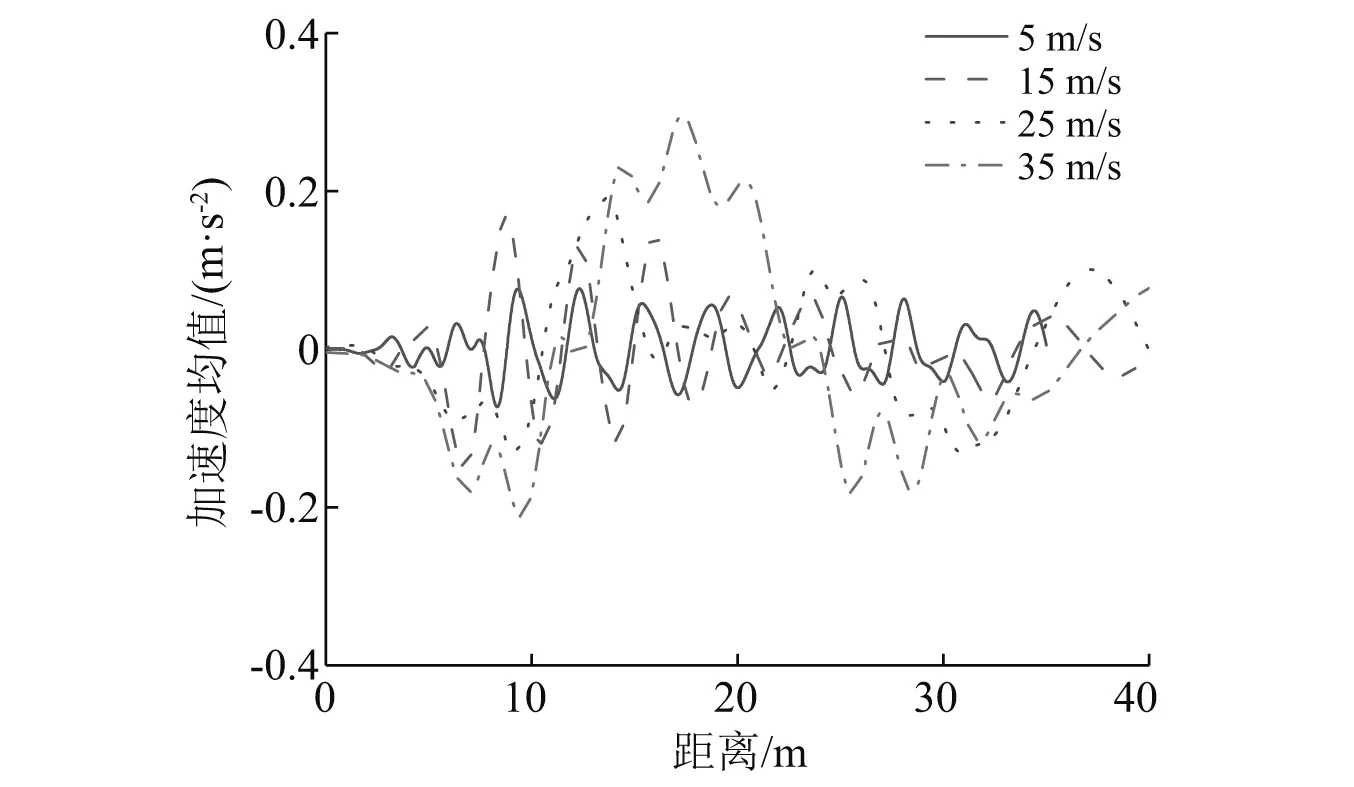
图9 车体竖向加速度均值

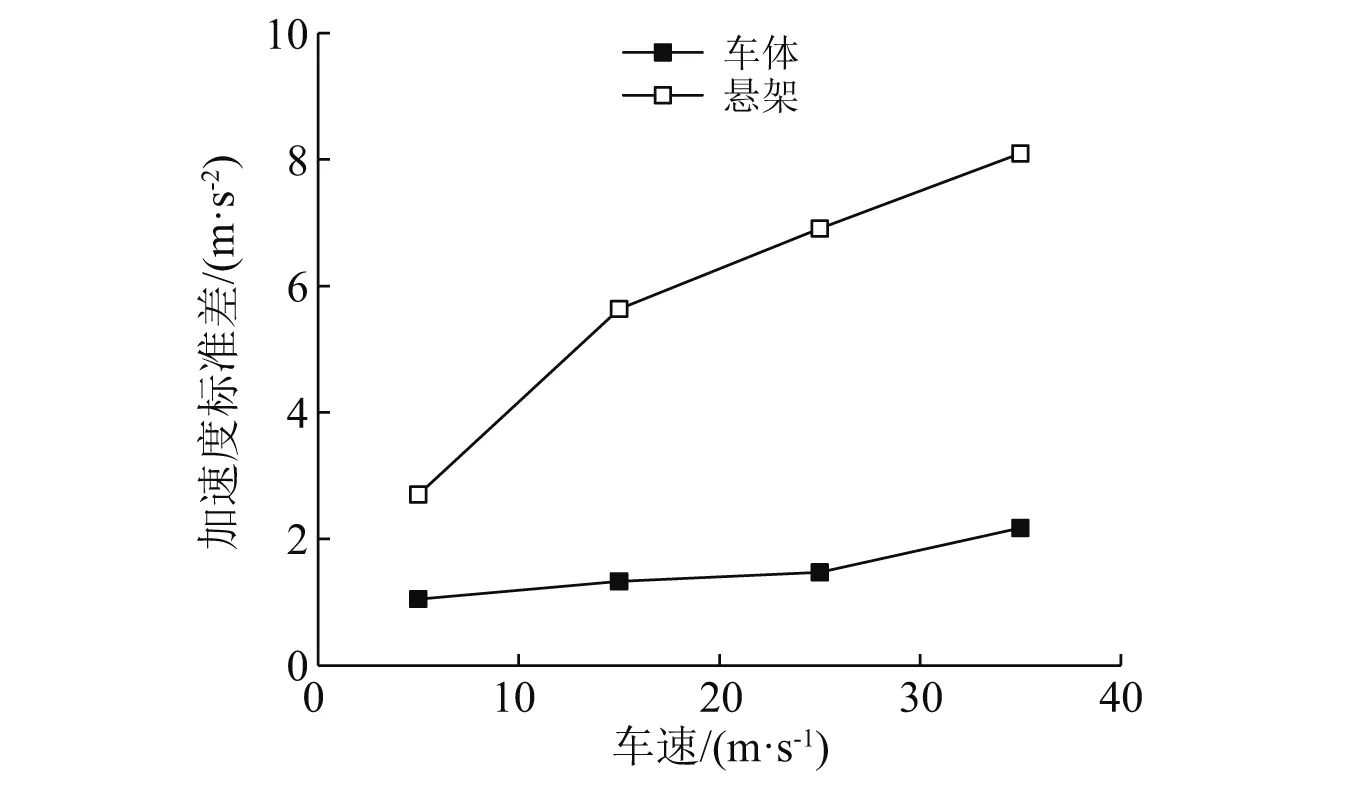
图10 车体、悬架竖向加速度标准差

图11为不同道路等级工况下汽车以不同速度通过桥梁时的车体垂向加速度概率最大值，可以发现，除了道路等级D和E以外，其他不同道路等级情况下，随着车速增大，汽车过桥的加速度基本上呈增大趋势。车体加速度随着道路等级变差而明显增大。

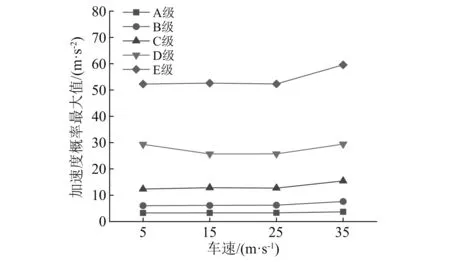
图11 车体垂向加速度概率最大值

5 结 论

通过引入概率密度演化方法建立了考虑桥面不平顺随机性的汽车-桥梁耦合振动模型，对比验证了模型的适用及效率，并对不同车速情况下系统随机响应进行了分析，得到主要结论如下：

(1)概率密度演化方法能够适用于考虑路(桥)面不平顺随机的汽车-桥梁耦合振动分析，与蒙特卡洛法的对比结果表明，在保证精度情况下，采用概率密度演化方法进行计算的效果能够提高1～2个数量级。

(2)车速对桥梁响应均值的影响不明显，总体上，随着车速增大，桥梁响应的标准差增大，高车速(35 m/s)下桥梁响应标准差最大值较中速度(15 m/s)提高了68%。不同道路等级工况下，桥梁位移概率最大值总体上都随车速增大而增大。在不同速度工况下，位移概率最大值随着道路不平度程度的加大而增大。

(3)在25 m/s车速以下，车速变化对车体位移响应均值影响较小，高速行驶(35 m/s)情况下，其位移响应均值较大，最大值相较于其他车速增大了约24%。而车体竖向位移标准差基本与车速随线性增大关系。车体竖向加速度响应的均值及标准差均基本随车速线性增大。除了道路等级D和E以外，其他不同道路等级情况下，随着车速增大，汽车过桥的加速度基本上呈增大趋势。车体加速度随着道路等级变差而明显增大。

(4)悬架的竖向位移响应的标准差最大值与车体基本一致，而其竖向加速度响应的标准差较车体大得多，在高车速(35 m/s)情况下，悬架的竖向加速度标准差为车体的3.7倍。