考虑含石量和坡度不同组分下颗粒流冲击刚性结构的力学模型研究
2021-07-22韩培锋苏有文
成 浩, 韩培锋, 2, 苏有文
(1. 西南科技大学 土木工程与建筑学院,四川 绵阳 621010; 2. 水利部山洪地质灾害防治工程技术研究中心,武汉 430010)
土石混合体(soil-rock mixture)是第四纪以来形成的,由一定工程尺度、强度较高的块石、细粒土体及孔隙构成的极端不均匀松散岩土介质系统;是一种介于均质土体和破碎岩体之间的复杂混合地质材料,在人类工程活动、地震和降雨等作用下,极易诱发滑坡或崩塌灾害[1-3]。据国家统计局最新统计[4],2005年—2017年间全国共发生地质灾害297 412起,其中滑坡和崩塌占比较高,而该类灾害物源体的内在因素(含石量)和外在条件(山体坡度)不同,则会造成不同程度的损失。图1(a)为2009-07-25T16:10国道213线汶川段彻底关大桥因山体滑坡,桥上7辆汽车连同桥面一起坠下河岸,导致都汶高速公路中断,造成6人遇难和12人受伤;此次灾害物源体的含石量及其所处的位置坡度均较大。图1(b)为2013-07-08T10:30都江堰市三溪村因山体滑坡,导致都汶高速公路中断,造成45人遇难和116人失踪;此次灾害物源体的含石量较小,但所处的位置坡度较大。

图1 山体滑坡后的现场照片
目前国内外学者对干颗粒介质冲击运动和冲击力学的研究主要集中在:①按冲击材料有滚石冲击力学模型和碎屑流(颗粒流)冲击力学模型。黄润秋等[5-6]研究认为影响落石运动特征最主要的因素是坡面形态和坡度,并对树木拦挡落石运动的能量消耗进行了探讨。何思明[7]在以典型滚石防护结构为原型的基础上研究了垫层材料的冲击特性,并推导了滚石冲击压力计算公式,为滚石防护结构设计提供了理论参考。Wang等[8]在对比分析多种形式的挡板及其挡流能力和挡流效果的基础上,提出了一种更加有效的新型弧形挡板阵列,从而为山区岩崩障板设计提供了实际的参考依据。Jiang等[9-10]通过实验研究了颗粒性质对冲击力的影响,揭示了碎屑流冲击刚性挡墙的物理机制,在定量分析了各个分力在总冲击力中的分布比例后,最后提出了碎屑流冲击力学模型。Adel等[11]通过数值模拟推导并验证了颗粒流对挡墙施加的平均冲击力学模型。②按被冲击对象有挡墙、棚洞等。Albaba等[12]利用数值模拟研究分析了碎屑流冲击挡墙过程中的微观力学机制。王东坡等[13]采用数值压痕试验,研究了棚洞顶板在滚石冲击下的动力响应,并提出了新型EPS垫层缓冲材料。
综上,学者们大多关注与坡面垂直的刚性结构冲击运动及其力学模型,而关于干颗粒流冲击与坡面非垂直刚性结构的力学模型研究较少。此外,在现场和文献调研中发现,在滑坡堆积体量级一致的情况下,含石量和坡度不同组分下对被冲击对象破坏影响有所差异。因此,在此研究背景基础上,采用离散元素法(discrete element method,DEM)构建三维DEM模型,研究含石量和坡度不同组分条件下的颗粒流对与坡面非垂直刚性结构的冲击力差异和冲击力学模型。
1 冲击刚性结构的DEM模型
1.1 Hertz-Mindlin无滑动接触模型
Hertz-Mindlin (no slip)接触模型是Cundall教授在学者Mindlin的基础上首次提出,目前广泛应用于解决准静力或动力条件下岩石力学运动问题,其计算性能准确、高效[14-16],如图2所示。图中:R1,R2分别为两颗粒的接触半径;P为接触圆半径;δ为接触变形量。

图2 理想状态的Hertz-Mindlin接触模型示意图
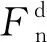
(1)
(2)
(3)
(4)
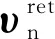
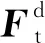
Ft=-Stδt
(5)
(6)
(7)

1.2 DEM模型建立
该模型主要由滑槽、料箱、刚性结构组成。其中:料箱和刚性结构沿滑槽中轴线设置,滑槽和刚性结构为全约束,保持静止状态;在整个颗粒流冲击过程中,忽略滑槽和刚性结构的弹性变形,只考虑颗粒与滑槽和刚性结构间的摩擦和碰撞作用。此外,颗粒流为固相,其整个运动过程都是在重力作用下进行,忽略外界阻力(如风力等)的影响。假定数值模型的几何尺寸为滑槽:长1 800 mm,宽350 mm,高300 mm;料箱:长400 mm,宽350 mm,高200 mm;刚性结构:长3 000 mm,宽2 000 mm,厚10 mm。颗粒密度2 100 kg/m3,滑体体积0. 028 m3,滑体总质量30 kg。
本文模拟试验的主要目的是针对干颗粒流冲击与坡面非垂直刚性结构这类灾害的动力学机制研究,同时考虑到颗粒单元在相互作用过程中的颗粒形状、时间步长等属性对模拟结果影响较大,故做如下假设:
(1)假定颗粒为有棱角形状的刚性颗粒,且颗粒的相互作用不会改变其几何形状,土颗粒的长宽高分别为7. 002 7 mm,5. 997 39 mm,4. 000 54 mm,单个块石颗粒如图3所示。
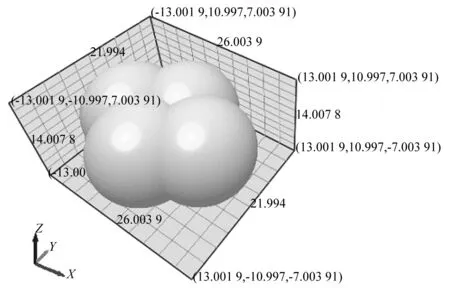
图3 模拟材料单个块石颗粒大样图(mm)
(2)有研究表明,时间步长设定在Rayleigh时间步长的5%~40%可以确保仿真过程的稳定[17];这里假定时间步长为6. 2661 6×10-5s。
综上,建立颗粒流冲击刚性结构的数值试验模型示意图,如图4所示。
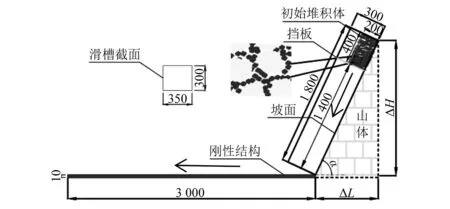
图4 冲击模型示意图(mm)
1.3 DEM模型计算参数标定
本文数值模拟材料参数是通过野外典型灾害点采集土石样品,开展了多组室内土工试验,对多组材料试验结果取平均值,并参考岩土材料等相关规范,最后获取了模拟材料的基本参数,如表1所示。数值模拟的接触参数则参照了前人的对于标定该参数的物理模型试验方法[18-22],通过对野外采集的土石样品,进行静摩擦因数与滚动摩擦因数的相关试验和数值模拟计算,并将结果进行对比,最后获得了颗粒接触的模拟参数,如表2所示。
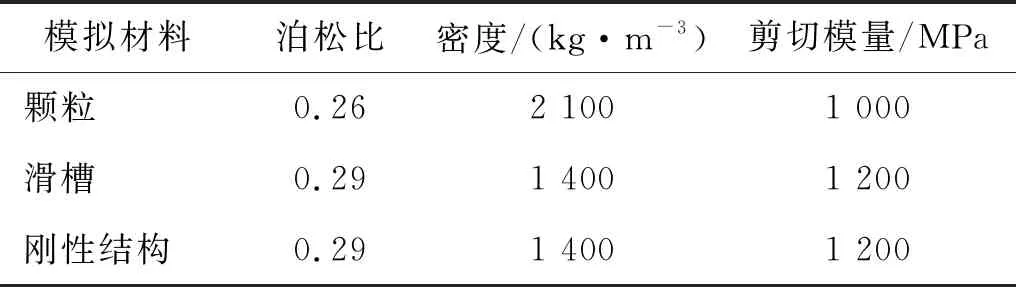
表1 材料属性
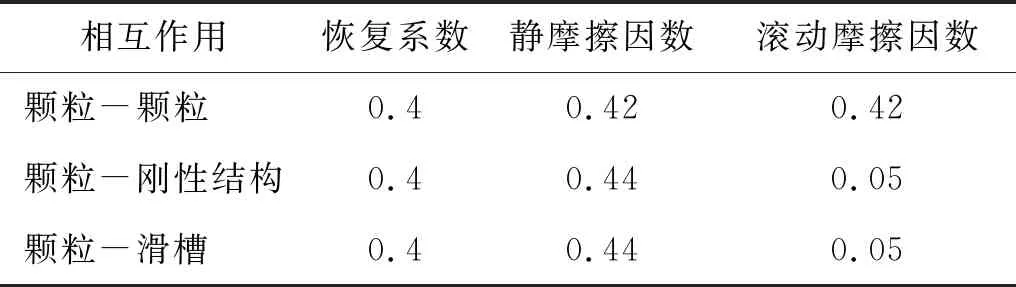
表2 接触属性
1.4 DEM模型试验设计
为探究颗粒流在含石量和坡度变化下冲击与坡面非垂直刚性结构的冲击动力学行为及冲击力力学模型。在进行数值模拟试验设计时,除了依据已有的野外调研资料外,对于坡度的选取还参照了樊晓一[23]对西南地区滑坡坡度分布特征的研究结论,对于含石量的选取则参照了舒志乐等[24]对土石混合体分形特性与含石量关系的研究结论,具体试验组分设计如表3所示。
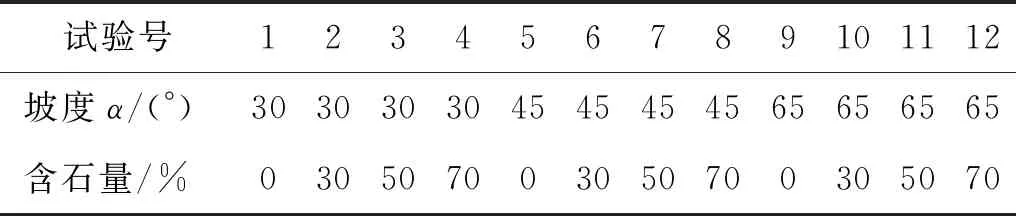
表3 冲击刚性结构试验组分设计
整个冲击过程的数值模拟分为三步:①设置参数和导入模型,生成初始堆积体;②打开料箱前缘挡板,堆积体在重力作用下对刚性结构施加冲击力的过程;③对模拟结果数据在线分析、导出数据计算分析及三维可视化整个冲击运动过程。
2 数值模拟结果与分析
2.1 颗粒流冲击过程分析
在数值模拟中发现,试验号12(坡度65°,70%含石量)组合下的颗粒流在冲击刚性结构时,冲击形式较为复杂,且速度变化较大,如图5所示。

图5 颗粒流冲击刚性结构过程
当t=0.86 s时,前缘颗粒以撞击形式冲击刚性结构,由于冲击较集中,可视为一个脉冲冲击;颗粒流以速度区分,前缘最大速度为5.11 m/s,中部次之,后缘较小,平均速度为3.74 m/s。其原因主要有:①前缘颗粒受约束较小,有很好的临空性和运动性;②后面颗粒在前面颗粒的阻挡下将一部分能量向前传递,从而持续性冲击。与垂直式刚性结构不同,在第一次冲击后,颗粒流不是爬升或回弹,而是弹跳后继续向前方运动。当t=1 s时,坡脚处底层颗粒速度急剧减小,这是由于底板阻碍形成的死区;后缘颗粒流在经过死区表层后冲击刚性结构,其作用面较大,可视为整体性冲击。当t=1.24 s时,只有部分颗粒对刚性结构翻滚撞击,速度由前缘向后缘递减。当t=2 s时,颗粒流的平均速度小于0.01 m/s,基本处于准静态堆积状态。
2.2 颗粒流冲击能量分析
冲击过程中能量的耗散反映了冲击力的内在变化。这里定义:动能耗散率Wk为t时刻颗粒流的总动能Kt与开始冲击时的总动能Ktol之比,可以写为
(8)
图6表明,随时间的推移,动能变化率曲线为先增长达到峰值后下降,直至动能耗完。在1.98 s,1.06 s,0.89 s后,含石量越大的动能变化率下降速度越快;可见含石量越大的颗粒流在冲击刚性结构时动能损失值越多。从曲线时程来看,坡度30°最大(0.35~2.69 s)、45°次之(0.35~1.73 s)、65°最小(0.35~1.5 s)。这就说明颗粒流随坡度的增大,就越早接触刚性结构,由于速度较快,则单位时间内的接触越频繁,能量消耗和动能损失值较大,对其冲击效果就越好。
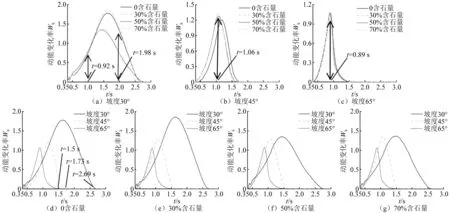
图6 颗粒流冲击刚性结构动能变化率时程
2.3 颗粒流冲击力时程与峰值分析
2.3.1 含石量对法向力时程与切向力时程的影响
图7和图8表明,随时间的推移,细颗粒土和土石耦合(指的是同一材料不同粒径代表土和石,在运动中的相互碰撞和能量传递效应,而非土石本构模型中的耦合)下的法向力时程与切向力时程走势均是先增长达到峰值,而后下降趋于准静态波动,最后形成残余力。法向力是颗粒流冲击刚性结构时竖直向上的力,法向力与切向力受刚性结构摩阻力的影响较大,当摩阻力大于其冲击力时,颗粒就会静止堆积;这就说明颗粒流冲击刚性结构是在某一时间段的连续性冲击。这里定义:冲击力时效是以最早出现冲击力的时刻为初始时间至最早出现稳定残余力的时刻为结束时间的时间段。由表4分析可知,基本上含石量较大的颗粒流冲击时效较短,单位时间内对刚性结构的法向力与切向力增大,其冲击破坏力有所增强。
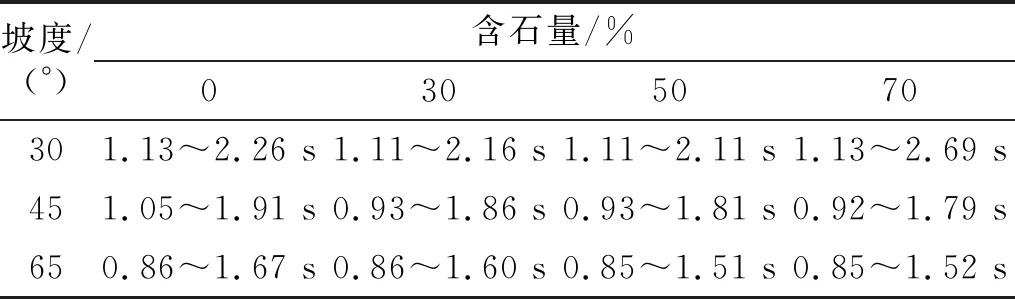
表4 法向力时效
由图7(j)~图7(l)、图8(j)~图8(l)可以观察到,土石耦合曲线出现了两次冲击力峰值;统计结果见表5。由于法向力与切向力的各自峰值差异相似,所以这里主要分析法向力。含石量对两次法向力峰值和峰值出现的时间均产生不同程度的影响,且两次峰值都随含石量的增大逐渐增大,第一次峰值较第二次峰值偏大约40%。

表5 坡度65°法向力峰值时刻及峰值
随着含石量增大,各冲击力程曲线波动越大;其中图7(l)土石耦合曲线逐渐波动到细颗粒土曲线的上方。这是因为含石量增大,颗粒间的空隙变大,促使颗粒间的碰撞次数增多,能量传递变得更加频繁。
。
2.3.2 坡度对法向力时程与切向力时程的影响
图7和图8表明,各冲击力时程走势均为先增长达到峰值,而后下降趋于稳定。随着坡度的增大,颗粒流冲击刚性结构的时间和峰值时间越早,法向力与切向力在下降阶段越显著且下降值增大;这就反映了坡度越大的颗粒流在冲击过程中,有效冲击较集中,其损失值就越多;坡度65°颗粒流的冲击力时程变化最强烈。坡度影响冲击力的原因主要是:①在坡面长度相同时,坡度越小的初始堆积体坡高也就越小,这就导致其重力势能和动能加速度随之减小,而在坡面运动过程中的摩擦耗能基本一致;②坡度越小时,颗粒的速度减小,其能量传递较弱,后缘颗粒在前缘颗粒的阻挡下还未冲击刚性结构就已静止堆积在坡面。
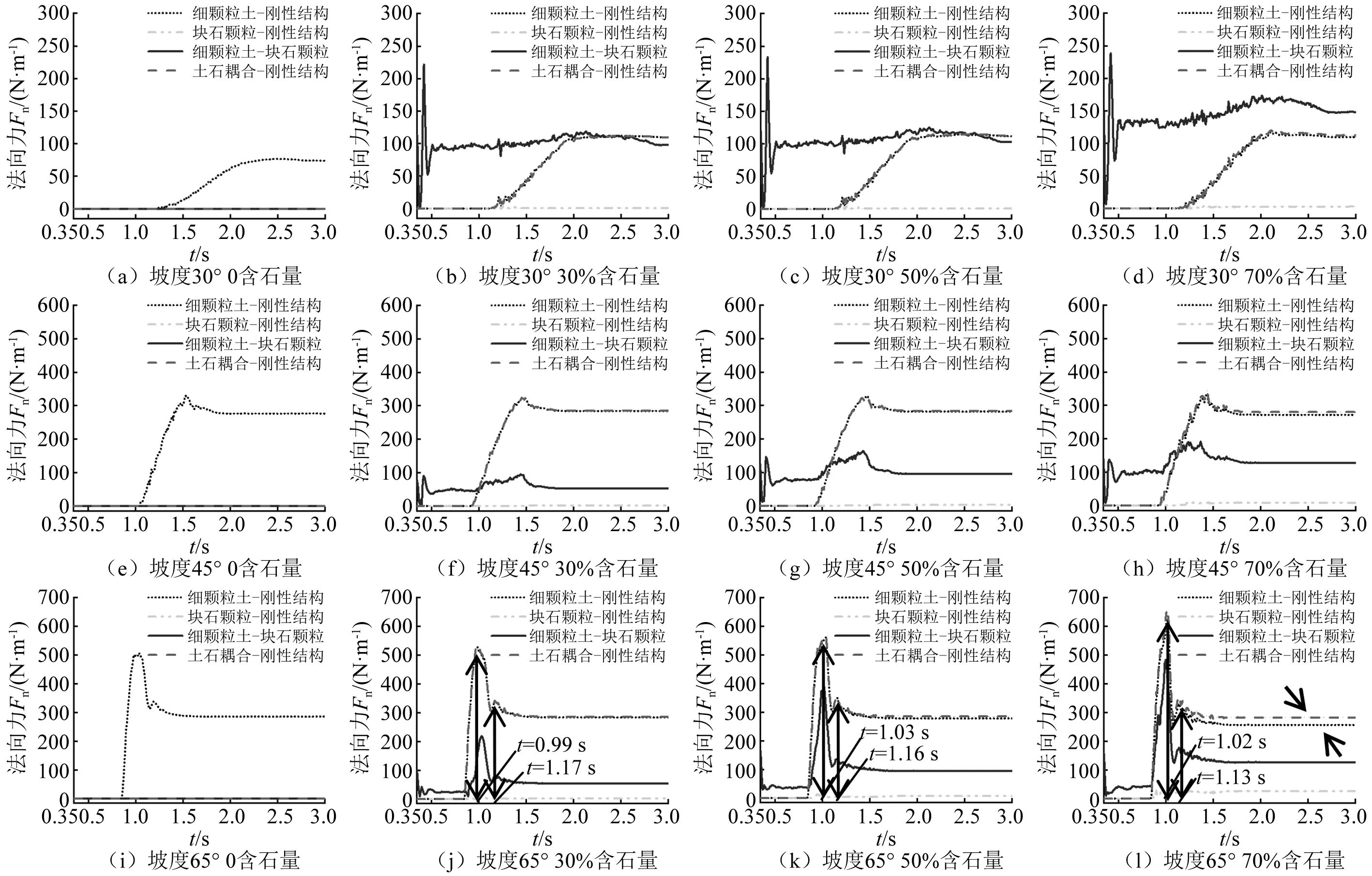
图7 不同组分条件下的法向力时程
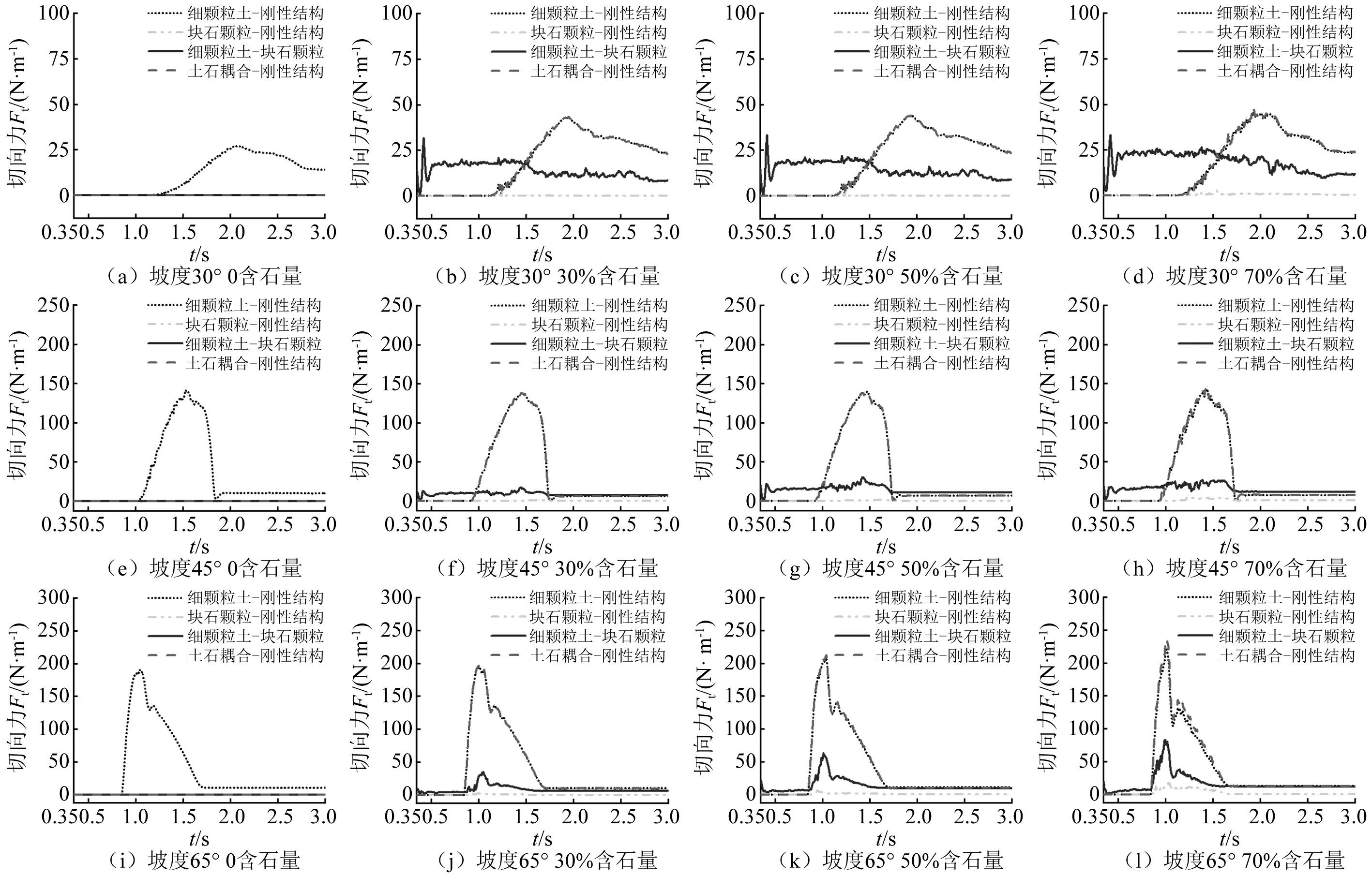
图8 不同组分条件下的切向力时程
2.3.3 含石量对冲击力峰值的影响
在冲击力时程分析中发现,土石耦合作用下的颗粒流比细颗粒土或块石颗粒单独作用对法向力峰值影响要大,其峰值范围依次是76.68~660.41 N/m,76.67~625.50 N/m,0~39.83 N/m。这是因为单独的细颗粒粒径较小,整体滑动性较好,以滑动冲击为主。单独的块石粒径较大,接触面积较小,以翻滚撞击为主。土石耦合作用下,细颗粒在块石位置不断更替产生足够的间隙下渗到颗粒流底部,形成一个较好的滑动带,包裹并携带块石运动;块石在运动中把自身一部分动能传递给周围的细颗粒,从而产生耦合效应持续性冲击刚性结构。所以后文重点讨论土石耦合作用下的颗粒流冲击。结合图9和表6分析可知,法向力与切向力峰值均随含石量的增大而增大,相应的峰值增幅越大;换句话说,含石量变化越大对冲击力峰值的影响程度越大。法向力远大于切向力,最大法向力为660.41 N/m,最大切向力为237.20 N/m。
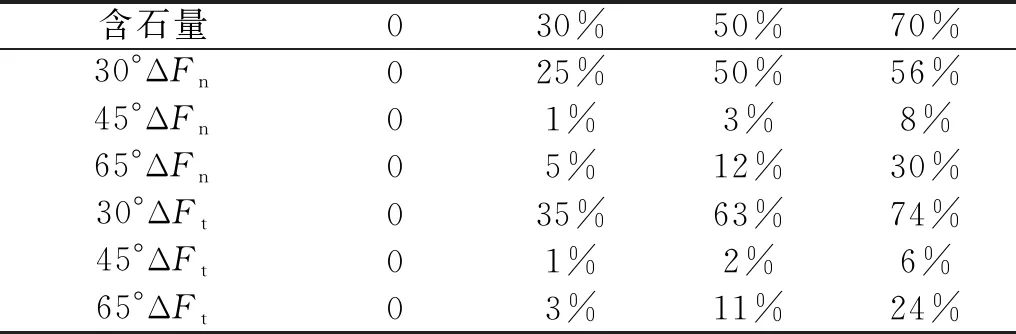
表6 含石量对冲击力峰值增幅的影响
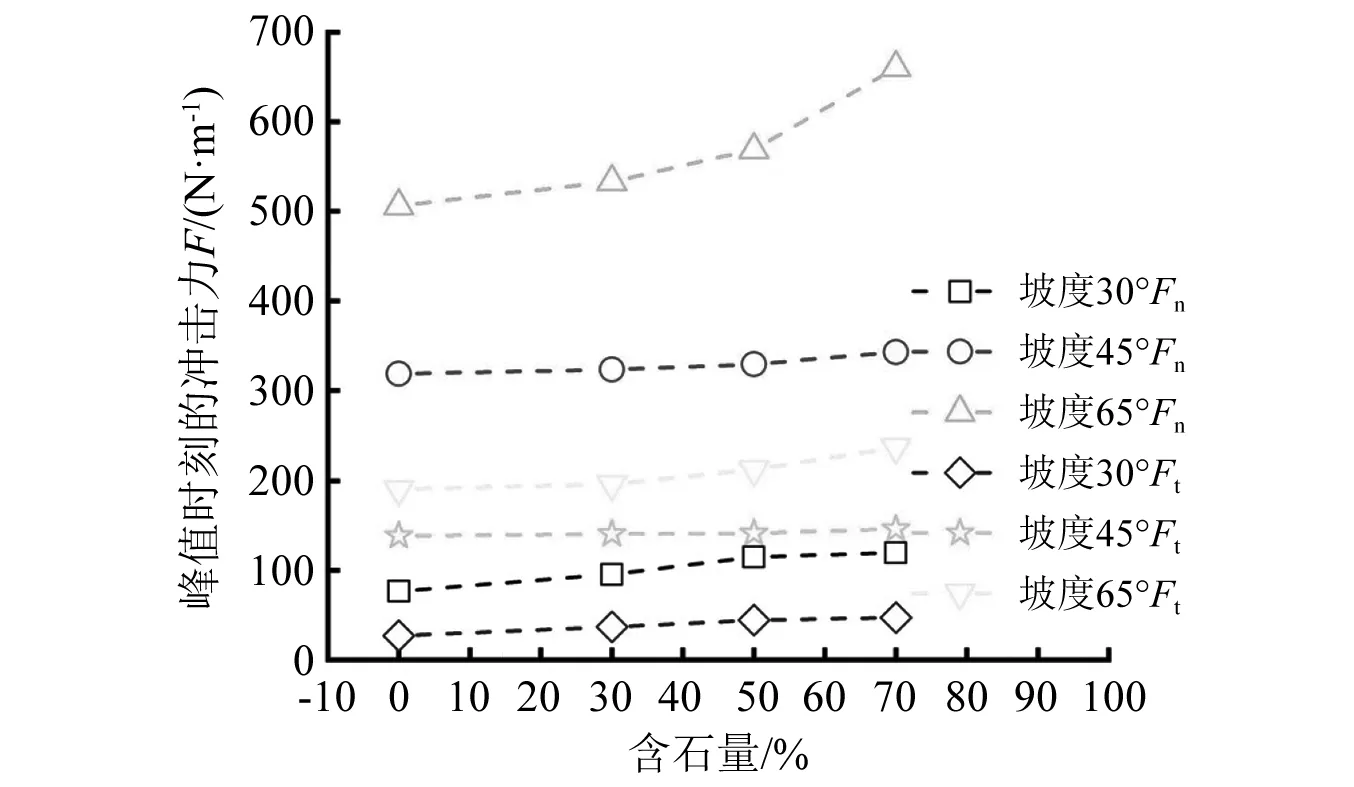
图9 峰值时刻的冲击力随含石量变化
2.3.4 坡度对冲击力峰值的影响
结合图10和表7分析可知,随着坡度的增大,颗粒流冲击力峰值曲线呈近似线性上升趋势,相应的冲击力峰值增幅越大。另外,对比表6和表7可知,含石量变化对冲击力峰值的影响程度远远小于坡度对峰值的影响程度。
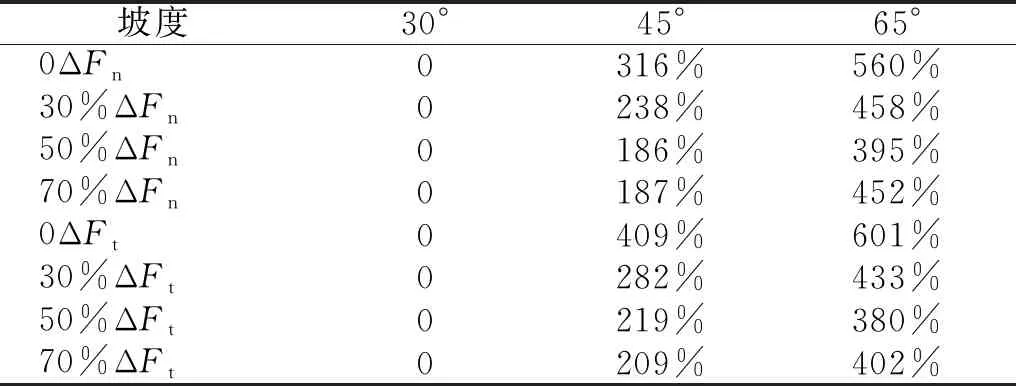
表7 坡度对冲击力峰值增幅的影响
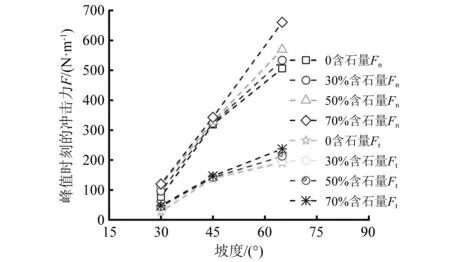
图10 峰值时刻的冲击力随坡度变化
2.3.5 峰值时刻的平均速度分布
图11表明,峰值时刻颗粒流的平均速度在0.18~2.24 m/s内变化,随着平均速度的增大,法向力与切向力均有不同程度的增大。可以观察到,峰值时刻的平均速度与法向力和切向力基本上沿坡度维度分布,当坡度达到最大时,平均速度、法向力和切向力离散最大。
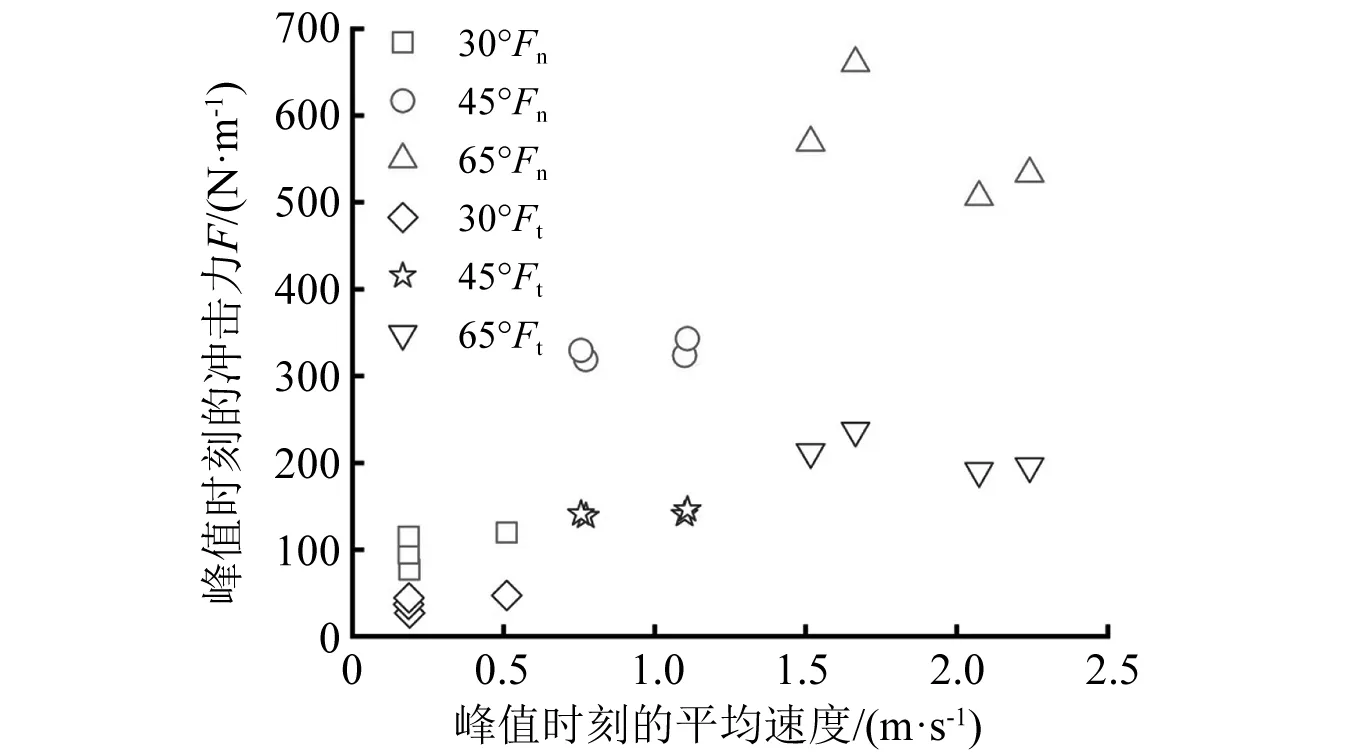
图11 峰值时刻的平均速度分布
2.3.6 峰值时刻的应力与压力分布
图12为峰值时刻刚性结构的应力与压力分布。分析可知,峰值时刻的应力与压力基本沿坡度维度分布,且随坡度的增大而增大,坡度对应力与压力的影响要大于含石量。随着法向力的增大,应力与压力都有不同程度的增大,当法向力最大时,应力与压力达到最大,分别为110.07 Pa,1 157.10 Pa。应力和压力与法向力的相关性系数R2分别为1和0. 977 61,这就反映了其相关性很好,换句话说,刚性结构的应力与压力主要取决于法向冲击力的大小。

图12 峰值时刻的应力与压力分布
3 冲击力学模型建立与分析
在对颗粒流冲击刚性结构的冲击过程、冲击能量、冲击力时程与峰值分析的基础上,进一步研究其冲击力学模型。在冲击力学模型建立与分析时,参照了Jiang等和Adel等的冲击模型。
Jiang等通过实验对干颗粒流冲击挡墙所产生的法向冲击力Fn进行力组分解
Fn=Fg+Fp+Fd
(9)
式中:Fg为死区重力和摩擦力共同作用的土压力;Fp为死区上流动层的静土压力;Fd为死区上流动层的冲击土压力。
其中,Fg是颗粒流在死区处形成的堆积体对挡墙产生的一个法向力,表达式为
(10)
式中:δ1为颗粒与滑槽基底的摩擦角;δ2为颗粒与挡墙的摩擦角;G为挡墙前堆积区颗粒流的重力。
Fp的表达式为
Fp=0.5kρgh2cosαw
(11)
(12)
式中:ρ为颗粒流密度,kg/m3;h为流动层厚度;α为坡度,(°);w为挡墙宽度m;k为被动土压力系数,Kwan等[25]建议直接取1;φ为颗粒流的内摩擦角。
根据Kwan等对死区流动层冲击土压力的推导Fd可以表示为
Fd=0.5ρv2CDAcosθ
(13)
式中:v为颗粒流流速,m/s;A为冲击受力面积,m2;CD为动土压力系数;θ为坡度,(°)。
CD可以表示为
CD=aFr-n
(14)
(15)
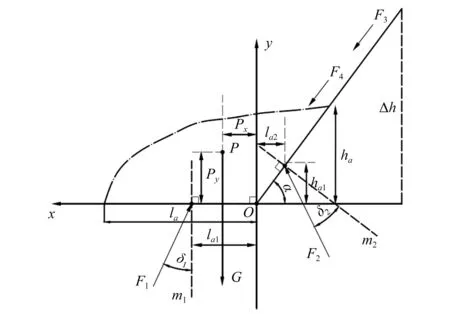
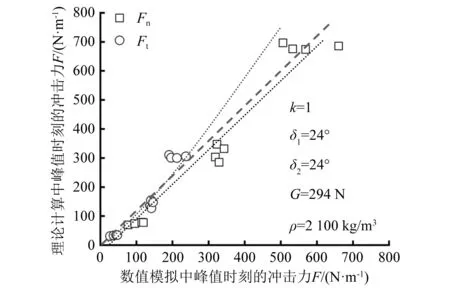
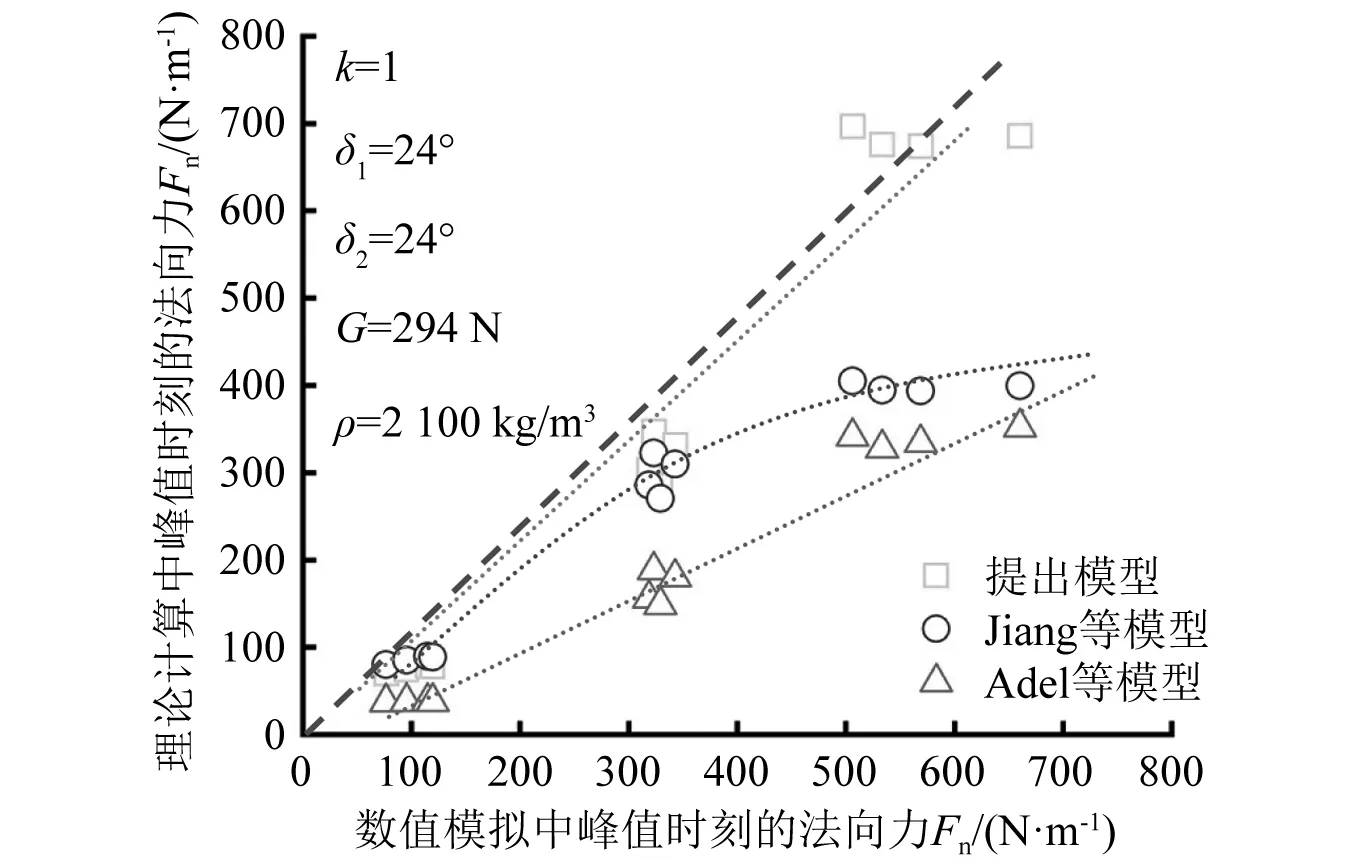
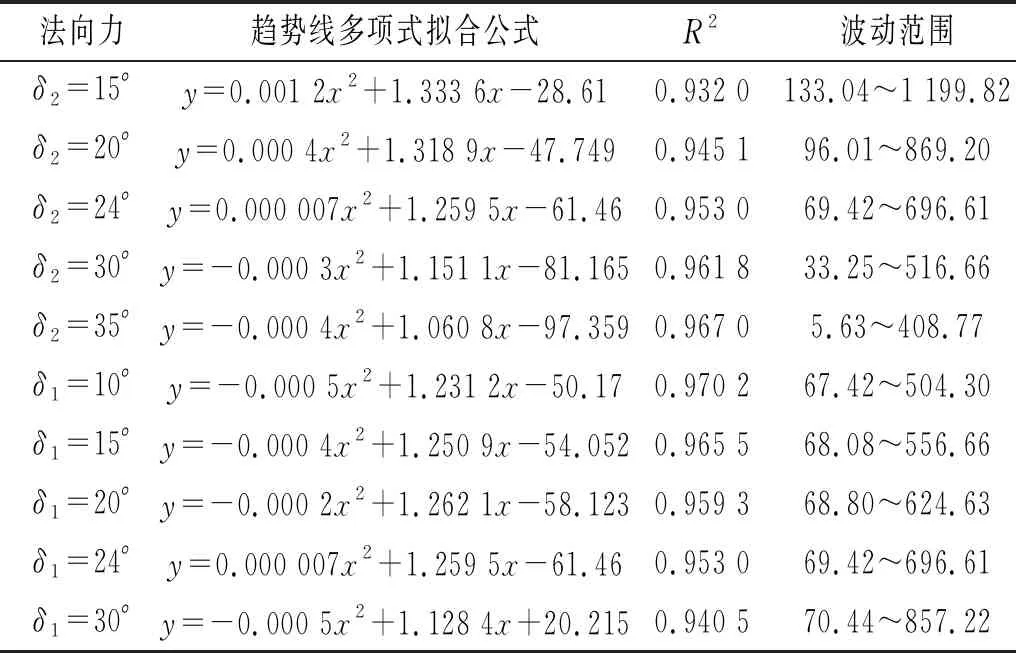
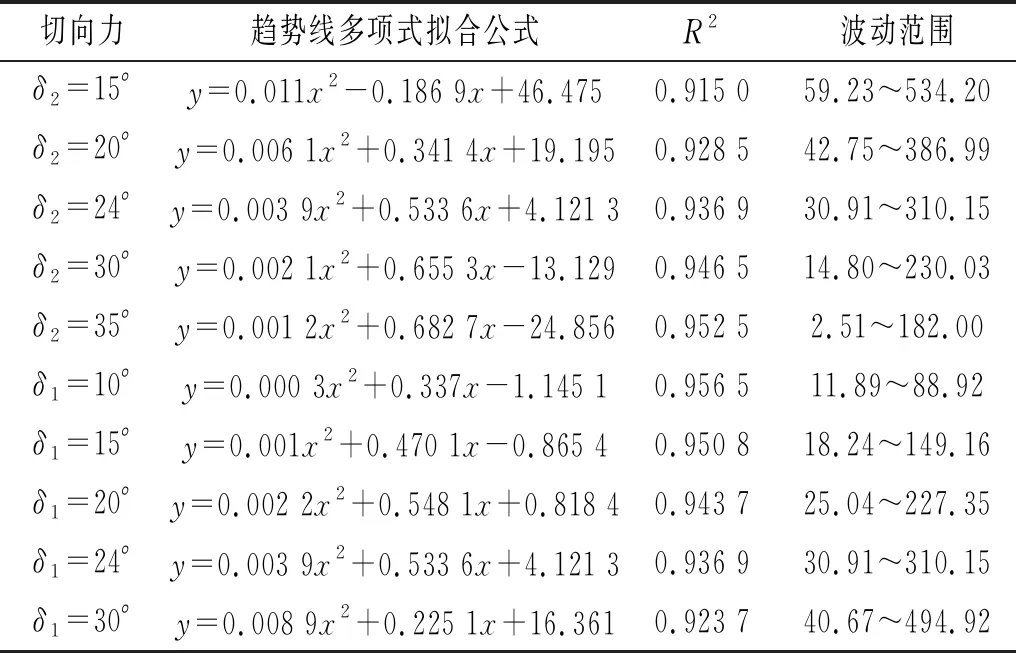
式中:Fr为弗劳德数;a和n为修正系数,当0.8 在另一个模型中,Adel等通过数值模拟计算验证了颗粒流对刚性挡墙造成的的平均冲击力,该模型总的法向力包含了死区的重力、滑槽基底的摩擦力和后续颗粒流对死区的冲击力Fs,其法向冲击力Fn表达式为 Fn=Fs+Gcosα(tanα-u) (16) (17) (18) 式中:φ2,φ1分别为峰值时刻颗粒流的体积分数,取0.6,0.4;u为库仑摩擦因数;h1,h2分别为颗粒流的平均流动厚度和表层稀释颗粒流的跳跃高度;v为颗粒流的速度。 3.1.1 峰值时刻冲击力公式推导 初始堆积体在重力作用下沿滑槽向下运动,在冲击刚性结构的过程中,达到最大冲击力的时刻称为峰值时刻。根据峰值时刻堆积体重心的位置坐标和几何形态,再运用静力平衡力学理论对刚性结构进行受力分析,进而建立冲击力学模型,如图13所示。图13中:P点为重心位置;Px,Py分别为P点的横纵坐标;G为重力;la1为冲击作用最大长度;F1,F2分别为刚性结构的反作用力和滑槽基底的反作用力;δ1,δ2分别为它们的摩擦角;F3,F4分别为颗粒流的冲击土压力和被动土压力;ha为峰值时刻堆积体的最大高度;α为山体坡度;Δh为初始堆积体的坡高。 图13 峰值时刻刚性结构的冲击受力模型 基于《理论力学》[27]静力平衡方程理论,根据力系平衡的充要条件,建立直角坐标系可得 ∑Fx=0 (19) ∑Fy=0 (20) ∑Mo=0 (21) 将图13中的冲击受力模型参数代入式(19)~(21),可得 F2sin(α-δ2)-F1sinδ1+F3cosα+F4cosα=0 (22) -G-F4sinα-F3sinα+F1cosδ1+ F2cos(α-δ2)=0 (23) -F1cosδ1la1+F2cos(α-δ2)la2+GPx- F2sin(α-δ2)ha1+0.5(F3+F4)la=0 (24) 通过计算可得到滑槽基底的反作用力F1;刚性结构的反作用力F2、最大法向力Fn、最大切向力Ft和最大作用距离la1的表达式为 (25) (26) Fn=F1cosδ1= (27) Ft=F1sinδ1= (28) (29) 3.1.2 峰值时刻冲击法向力与切向力分析 图14为数值模拟与理论计算中峰值时刻总的法向力、总的切向力结果比较。表8为总的法向力与切向力相关性检验计算结果。分析可知,法向力、切向力的相关性系数R2分别为0.953 0,0.936 9,可见二者的相关性R2越接近1,就代表其拟合越好。从趋势线斜率来看,法向力斜率较切向力斜率偏小,但二者斜率都无限接近平衡线;这就说明本文所提模型的法向力、切向力理论计算结果与数值模拟的结果基本相符。 图14 理论计算的冲击力结果与数值模拟结果比较 表8 法向力、切向力的相关性检验 图15为本文模型与Jiang等模型和Adel等模型在峰值时刻总的法向力计算结果比较。表9为多模型法向力相关性检验计算结果。分析可知,三者法向力的相关性系数R2趋于1,其拟合越好。从趋势线斜率来看,本文模型与Jiang等模型的法向力计算结果差异较小,而Adel等模型计算结果则较数值模拟结果明显偏小。这是因为在Adel等模型中,计算式(式(17))后续颗粒流对死区冲击所产生的力(Fs)偏小,最后导致计算式(式(16))总的法向力(Fn)偏小。此外,坡度变化对模型计算结果的影响不可忽视,本文模型和Adel等模型的计算结果与坡度基本呈线性正相关;而Jiang等模型则与坡度呈非线性关系,且随着坡度的增大,法向力增大的趋势变缓。 图15 多模型的法向力比较 表9 多模型的法向力相关性检验 考虑到滑槽基底摩擦角δ2对最大法向力与最大切向力的影响,δ2分别取15°,20°,24°,30°,35°;刚性结构摩擦角δ1取24°,计算结果如图16(a)、图16(b)所示。δ2,δ1变化对法向力与切向力的相关性检验见表10和表11。分析可知,随着δ2的增大,法向力与切向力逐渐减小,趋势线斜率逐渐减小,相关性系数R2拟合很好;从趋势线相较于平衡线的离散性来看,随着δ2的增大,当δ2<24°时,趋势线逐渐靠近平衡线;当δ2>24°时,趋势线逐渐偏离平衡线。 在滑槽基底摩擦角δ2取24°的基础上分析刚性结构摩擦角δ1对最大法向力与最大切向力的影响,δ1分别取10°,15°,20°,24°,30°的计算结果如图16(c)、图16(d)所示。结合图表分析可知,随着δ1的增大,法向力与切向力逐渐增大,相关性系数R2呈逐渐减小的趋势。从趋势线相较于平衡线的离散性来看,随着δ1的增大,当δ1<24°时,趋势线逐渐靠近平衡线,当δ1>24°时,趋势线逐渐偏离平衡线。可以观察到,法向力趋势线基本分布在平衡线附近,而切向力趋势线基本分布在平衡线下方;这就说明刚性结构摩擦角δ1对法向力的影响较小,而对切向力的影响则较大。这是因为在法向力的计算式(见式(26))和切向力的计算式(见式(27))中,当δ2取24°时,随着δ1的增大,cosδ1较大并随之减小,而sinδ1较小并随之增大,cos(δ1+α-δ2)势必减小。 图16 δ2,δ1变化对法向力与切向力的影响 进一步对比分析滑槽基底摩擦角δ2和刚性结构摩擦角δ1对最大法向力与最大切向力的波动范围及影响程度,分别取15°,20°,24°,30°,见表10和表11。数值模拟的法向力与切向力范围分别为76.68~660.41 N/m,27.18~237.20 N/m。分析可知,δ2和δ1无论谁单独增大,其理论计算的法向力波动范围相较于数值模拟范围均呈现出先减小再增大;而切向力波动范围相较于数值模拟范围则有所差异,分别表现为逐渐减小和先减小再增大。当δ1和δ2取值小于24°时,δ2的法向力和切向力波动范围大于δ1,说明δ2较δ1对法向力和切向力的影响显著;当δ1和δ2取值大于24°时,δ1的法向力和切向力波动范围大于δ2,说明δ1较δ2对法向力和切向力的影响显著。 表10 δ2,δ1变化对最大法向力的影响 表11 δ2,δ1变化对最大切向力的影响 综上所述,本文所提模型选取的滑槽基底摩擦角δ2为24°和刚性结构摩擦角δ1为24°的法向力与切向力计算结果与数值计算的结果基本吻合,同时与Jiang等模型和Adel等模型的冲击量级较为一致,说明颗粒流冲击非垂直刚性结构的模拟结果是有效可行的。 本文考虑含石量和坡度不同组分下开展颗粒流冲击与坡面非垂直刚性结构的数值模拟试验,在对冲击过程、冲击能量、冲击力时程与峰值、应力与压力分析的基础上,建立了峰值时刻冲击力力学模型,推导并验证了峰值时刻冲击力公式。得出以下主要结论: 含石量越大、坡度越大的颗粒流在冲击刚性结构时,动能变化率耗时越短,单位时间内动能损失值越多,法向力与切向力曲线波动越大。土石耦合作用下的颗粒流比细颗粒土或块石颗粒单独作用对法向力峰值影响要大。含石量对最大法向力与最大切向力的影响程度较坡度小。峰值时刻的平均速度、应力与压力大致沿坡度维度分布,刚性结构的应力与压力主要取决于法向冲击力的大小。所以,在野外监测滑坡或崩塌堆积体时,应该重点关注该类含石量较大、坡度较大的土石混合体斜坡。 本文所提模型选取的滑槽基底摩擦角δ2为24°和刚性结构摩擦角δ1为24°计算的法向力和切向力与数值模拟结果基本相符。在理论计算中,刚性结构的摩擦角δ1对切向力的影响较大,应当予以重视。当δ2和δ1取值在15°~30°内,取值小于24°时,δ2较δ1对法向力和切向力的影响显著;相反大于24°时,δ1较δ2对法向力和切向力的影响显著。3.1 峰值时刻冲击力公式推导与分析
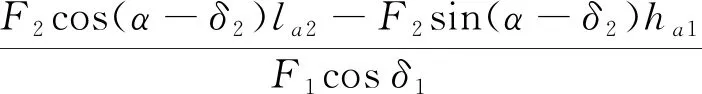


3.2 冲击力学模型参数分析

4 结 论
