采用机器学习方法评估流线型箱梁颤振临界风速

梅瀚雨， 王 骑,2， 廖海黎,2， 刘珉巍

(1.西南交通大学 桥梁工程系，成都 610036；2.西南交通大学 风工程四川省重点实验室，成都 610036)

现代桥梁结构向跨度更大、更柔的方向发展，这将使得其结构刚度小、阻尼低而对风荷载的敏感性逐渐增加。在大跨度桥梁抗风设计过程中，颤振性能是尤为关键的设计控制因素。对于流线型箱梁而言，由于其各方面气动性能优越(颤振、涡振等)且制造工艺成熟，目前已在多座大跨度桥梁中使用[1-4]。一般地，在桥梁设计初期，设计者可利用自由振动风洞试验或数值模拟计算流体力学(computational fluid dynamics, CFD)方法可以较为准确地评估桥梁断面的颤振性能。然而，目前风洞试验的成本较高、试验周期长，CFD技术仍存在精度不够、计算成本较大等问题。另一方面，基于Scanlan等[5]提出的线性自激气动力理论并结合断面的颤振导数，也可以在桥梁设计初步阶段较为快速地掌握其气动性能，但此类颤振分析方法推广至工业领域仍存在一定的障碍，例如：颤振导数的获取仍无法摆脱风洞试验。尽管公路桥梁抗风设计规范[6]或目前已有的一些快速预测流线型向量颤振临界风速的方法[7]较为便捷，但此类简化计算公式仍然存在参数识别困难、精度不足等问题。

机器学习方法是一种基于数据驱动的数据挖掘方法，近年来被学者广泛应用到风工程领域。顾明等[8]在2003年利用神经网络预测了某大跨屋盖表面平均风压；Jung等[9]利用神经网络识别了多种断面形式的颤振导数；Lute等[10]在2009年利用支持向量机识别了桥梁断面颤振导数并计算了颤振临界风速，相比于简化公式的计算结果，该方法在3座已建成桥梁上的预测精度更高；Wu等[11]利用基于元胞机优化的人工神经网络预测了桥梁断面在紊流下的加速度响应时程，其结果并不理想，究其原因在于人工神经网络模型不能有效挖掘输入时间序列的隐含信息；Yu等[12]利用Elman神经网络对短期风速进行了多步预测；李维勃等[13]利用径向基函数对冷却塔风场进行了重构；Huang等[14]基于BP神经网络并结合本征正交分解(principal components analysis,POD)，对建筑高层表面风荷载进行了预测；Li等[15]基于现场实测数据，利用决策树模型和支持向量机回归对大跨度悬索桥涡激共振事件分别进行了模态分类的模型构建和涡振响应回归模型的构建，其预测精度较高，该研究结果对于结构健康监测系统有极大的实用价值；李乔等[16]在2003年利用人工神经网络系统识别了桥梁断面的静力三分力系数，但由于当时人工神经网络模型的发展未得到充分的重视，其模型本身仍存在较大的提升空间，例如激活函数的选取、数据预处理的方式等。陈讷郁等[17]基于同济大学既有大跨度桥梁试验数据成果并利用人工神经网络，识别了扁平箱梁和倒梯形箱梁的三分力系数和颤振导数，其结果表明：人工神经网络模型对于三分力系数的预测精度符合预期，但对颤振导数的预测精度较差。

以上研究成果表明，机器学习算法可以有效地与风工程学科进行交叉，且研究结果对工程设计有较高的参考意义。然而，以上众多的研究均只考虑了单个机器学习算法，实际上，不同的算法所擅长的问题各不相同。另外，数据预处理、模型训练方法、算法超参数调优等问题的处理方式也不够完善。考虑到流线型箱梁断面相比于其他类型断面(例如：桁架梁、Π型梁等)更具有整体性，断面的试验模型更易于制作，且断面信息较易于量化描述，基于此，本文旨在利用机器学习算法所具有的强大的非线性映射拟合能力以及预测能力(或泛化能力)，分别采用4种典型的机器学习方法实现流线型箱梁断面的颤振临界风速预测，包括支持向量机回归模型、神经网络回归模型、随机森林回归模型和高斯过程回归模型，并基于评价结果进行最终的模型比选。本文结果表明：利用支持向量机回归建立的预测模型最优，且在实际桥梁断面上的预测精度最高。通过与现有规范中的颤振简化计算公式进行比较发现，本文的机器学习算法更为便捷，且其精度更能够满足工程设计需求。相比于前有的研究而言，本文的研究更具系统性，模型的选择和实现过程更为全面。因此，在本文建立的流线型箱梁断面颤振临界风速数据库的基础上，机器学习方法，尤其是支持向量机回归方法，能够在不进行风洞试验或者数值模拟计算的前提下，快速获取给定流线型箱梁断面颤振临界风速，且精度能够满足工程设计要求，这对于桥梁设计初期的抗风设计具有参考意义。

1 数据准备

1.1 风洞试验

本次试验以15种不同尺寸的典型流线型箱梁断面作为研究对象，断面长度L和宽度B分别均为1 100 mm和400 mm。选取了3种高度H=36 mm, 44 mm, 57 mm、即宽高比B/H分别为11， 9和7的三组断面，标记为FA组，FB组和FC组，每组断面设置5种不同的斜腹板倾角θ，分别为24°, 21°, 18°, 15°, 12°，未安装边缘栏杆的三组施工态断面(裸梁，记为Group1)如图1所示，从上至下标记为FA1～FA5；安装有边缘栏杆的成桥态断面(记为Group2)以及栏杆详图如图2所示(以FA1断面示例，其余断面均在相同位置安装相同尺寸的栏杆)。需要说明的是：栏杆的设置是为了交通安全需求考虑，其尺寸外形大同小异，本文的栏杆源于某大跨桥梁实际栏杆，具有普遍性。

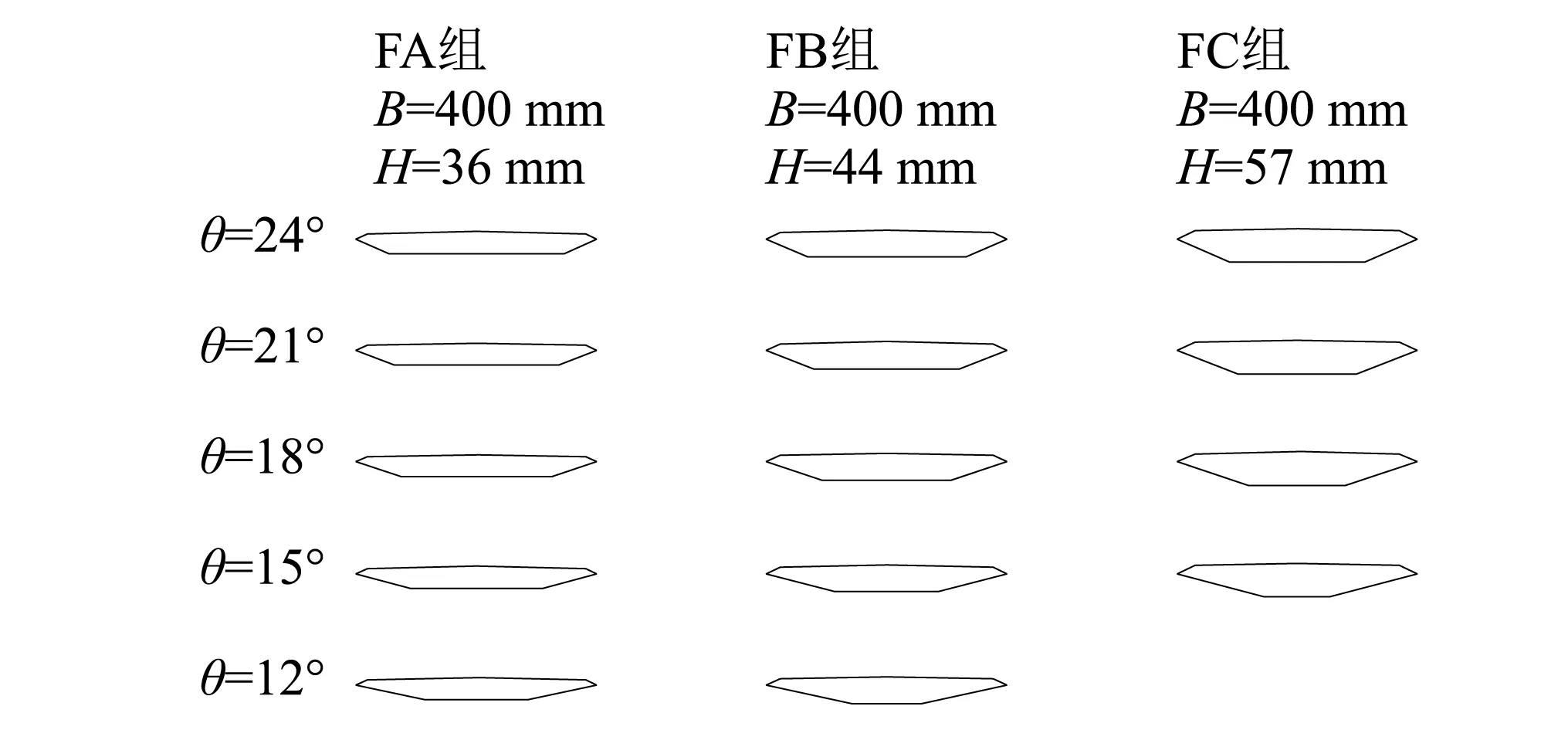
图1 流线型箱梁断面(Group1)示意图

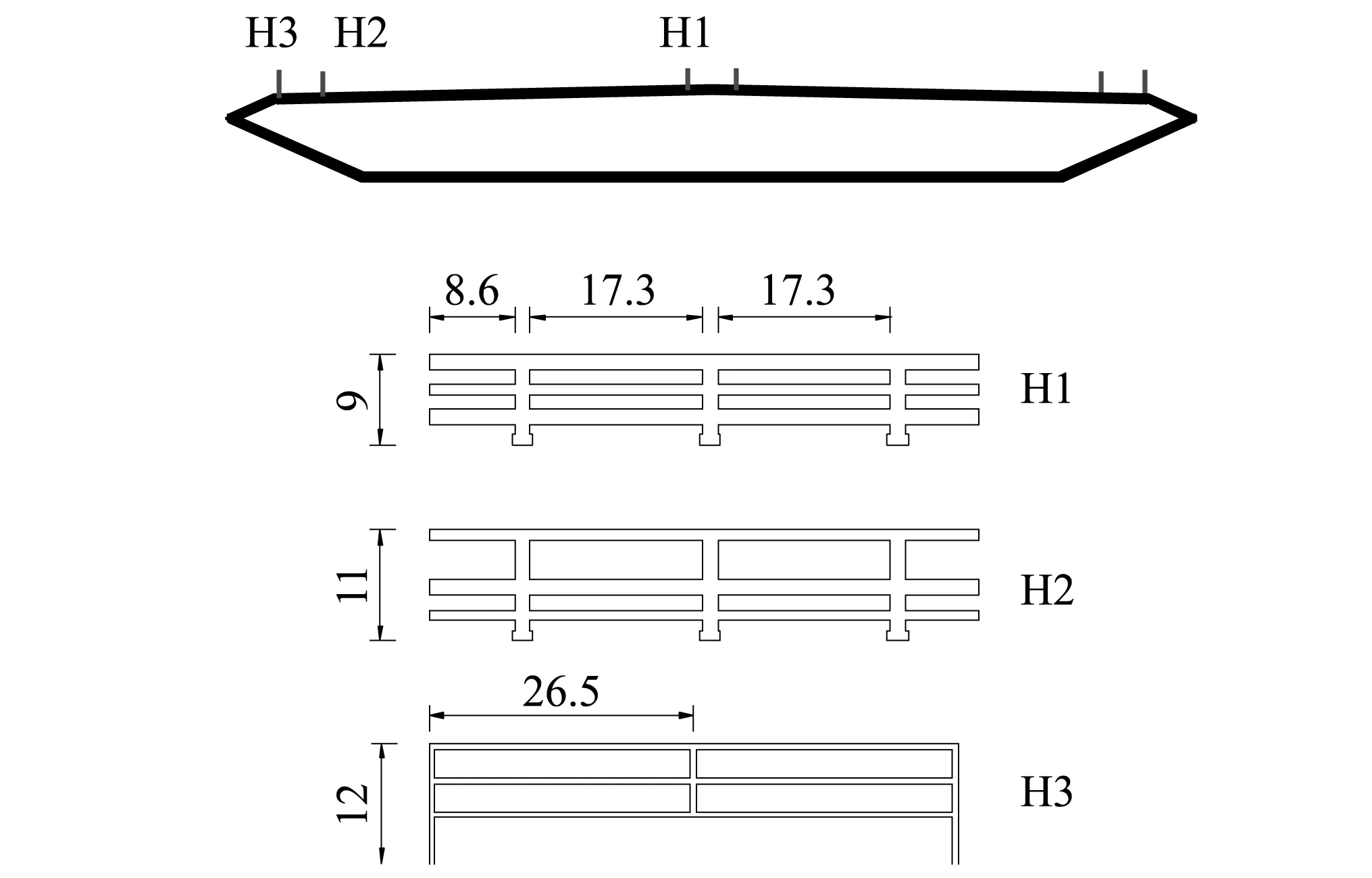
图2 栏杆模型详图(mm)

采用传统的弹簧悬挂节段模型系统进行动力试验，模型端部安装端板以保证二维来流，安装在风洞中的模型如图3所示。在 XNJD-2 风洞中进行了均匀流下节段模型自由振动风洞试验，试验过程中直接升高风速直至断面颤振发散以记录颤振临界风速Ucr。试验测试了不同断面在5个不同风攻角α=0°,±3°,±5°的颤振临界风速。

图3 安装在风洞中的节段模型

1.2 特征选择及数据处理

目前，特征参数的选取仍然依赖于先验知识的涉及。根据弯扭耦合颤振机理[18-19]，流线型箱梁断面的颤振临界风速除了与断面的气动外形有直接关系，还与一系列动力参数有关(这里仅考虑二维情况)，例如：模态频率、阻尼比、等效质量等。

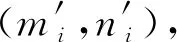
(1)

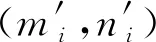
另一方面，与动力系统相关的参数包括竖向和扭转频率fv和ft，竖向和扭转阻尼比ξv和ξt，单位长度等效质量M和质量惯性矩Im。在节段模型风洞试验过程中，针对不同的模型选择不同的动力参数，以使机器学习算法感知范围更广，进而使得预测模型获得更强的鲁棒性。限于篇幅，部分试验模型动力参数见表1所示。

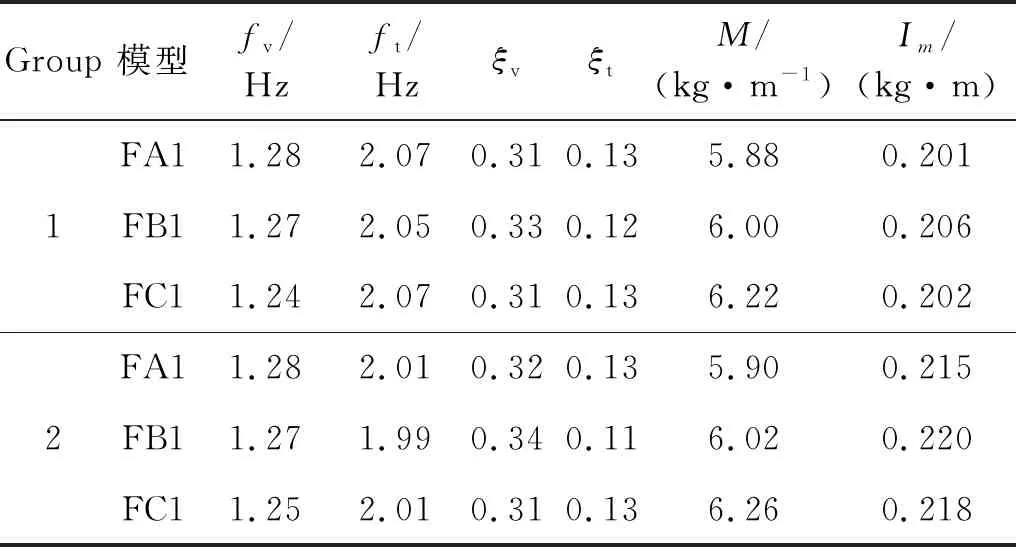
表1 动力试验参数

一般地，原始训练数据中，不同维度特征的来源及量级和量纲不同，会造成特征值的分布范围过大，训练效率较低。因此，必须先对样本数据进行预处理，才能获得较为理想的结果。本文选取标准归一化方法，将每一维度的特征都处理为符合标准正态分布。对于每一维度特征x，标准归一化后的新特征值可表示为

(2)

式中，μ(x)和σ(x)分别为每一维度特征值的均值和标准差。在标准归一化后，每一维度特征值都将服从标准正态分布。

值得注意的是：实际桥梁断面一般为对称结构，故顶点B和G、C和F、D和E坐标所暗含的信息是相同的。为了达到减少冗余输入信息和输入特征维度的目的，提高模型的泛化能力和收敛速度，只保留A、B、C和D点坐标作为输入特征。

综上：本文选取的Group1施工态断面输入特征包括4个顶点坐标，即8个特征，以及6个与动力参数相关的输入特征，总共14个输入特征。由于Group2的成桥态断面上的栏杆均设置相同尺寸，故输入特征维度与Group1相同，为14。Group1和Group2的输出目标均为颤振临界风速Ucr，即维度为1。

2 机器学习算法简介

2.1 支持向量机回归(SVR)

支持向量机回归(support vector regression，SVR)是基于支持向量机(support vector machine，SVM)分类模型发展起来的一种建立在统计学原理基础上的机器学习算法，广泛应用于统计分析或回归分析。其策略是基于间隔最大化(或添加惩罚参数C的软间隔最大化)并形成一个求解凸二次规划的问题，利用核技巧将输入特征空间映射到更高维的特征空间，进而利用线性回归方法来达到可以解决非线性问题的目的。该算法的优点在于最终的决策函数只由少数的支持向量所确定，且计算复杂度取决于支持向量的个数，这就使得该模型具有较好的鲁棒性。然而，SVR模型对于具有大规模训练样本的问题难以实施。相关的算法介绍及推导可参考文献[20-21]。本文选取高斯径向基函数(radial basis function，RBF)作为核函数(式3)

(3)

式中：K(x,x′)为核函数；γ为超参数；‖·‖为平方欧几里得距离。

2.2 神经网络(NN)

近年来发展迅猛的深度学习策略(deep learning)在人脸识别、机器翻译等领域应用广泛[22-23]，其核心思想正是基于神经网络算法(neural network，NN)，主要包括全连接前馈神经网络、卷积神经网络、循环神经网络等。神经网络模型具有极为强大的非线性映射能力，且随着训练样本、网络层数和神经元个数的增加，模型的性能逐渐提升，但这也导致了其参数规模过大、模型复杂度较高、模型训练成本较高等问题。本文选取回归分析最为常用的全连接神经网络对该问题进行处理。构造如图5所示的神经网络架构，输入神经元维度为20，包含两层隐含层，每层隐含层有64个神经元(为简洁起见，图中只包含8个隐含神经元)，激活函数σ(x)为ReLu函数，如下式所示。最后连接到含有一个线性激活函数的输出神经元以输出颤振临界风速Ucr。利用梯度下降法最小化如下损失函数(式5)并利用反向传播算法更新每个神经元的权值，最终获得最优回归模型。

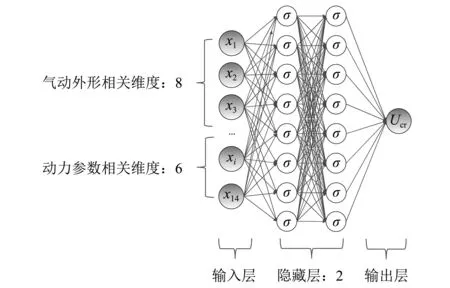
图5 全连接神经网络示意图

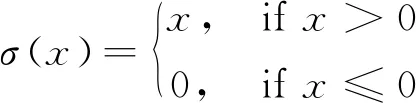
(4)

(5)

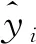
2.3 随机森林回归(RFR)

随机森林回归(random forest regression，RFR)是属于集成学习的一种机器学习算法[24]，其大致思路是训练多个决策树(decision tree)模型(弱模型)并打包组成一个强模型。基本思想是在训练阶段利用自助抽样从输入训练数据集中划分多个不同的子训练集来依次训练多个不同决策树，并在预测阶段将内部多个决策树的预测结果取均值得到最终的结果。相比于弱模型来说，该最终结果具有更强的鲁棒性和稳定性，且该算法对超参数的选取不敏感，对特征选择的依赖性较低，因此较为容易得到性能良好的模型。然而，随机森林方法容易在噪声较大的数据集上产生过拟合现象，即：在训练集上表现较好，在测试集上表现较差。同样地，本次模型训练将式(5)作为该模型的损失函数。

2.4 高斯过程回归(GPR)

高斯过程回归(Gaussian process regression，GPR)是基于统计学理论和贝叶斯理论发展起来的一种机器学习方法[25]，较为适用于处理高维度、小样本和非线性等复杂的回归问题，但当特征维度较高时，该算法表现性能较差。高斯过程回归的基本思想是假设任意有限个随机变量均满足高斯分布，其性质完全由均值函数和协方差函数确定。一般地，为简化计算，将均值设为0，协方差函数可以选择与SVR中相同的RBF核函数，通过极大似然估计可以实现对核函数中超参数的计算，并最终得到预测值。

3 模型训练

3.1 训练方法

本次训练的Group1和Group2断面数据集大小均为75，对两组数据集进行独立地建立机器学习模型。在划分数据集的过程中，数据的分布会显著影响最终的评估结果。一般地，训练集应与测试集互斥，即测试样本完全独立于训练集。将数据集按7 ∶3比例随机划分为训练集和测试集(“留出法”)。其中，训练集用来对模型进行训练，测试集用来对模型进行最终的性能评价。因此，训练集大小为52，测试集大小为23。

在数据量充足的情况下，利用经过多次随机划分的数据集进行训练和评估，“留出法”足以获得较好的模型构建。然而，考虑到数据样本量较小，且期望最大化利用数据样本，本次研究将以上留出法所得的训练集再一次划分为k个子集，其中k-1个子集用于训练，剩余子集(验证集)用于模型的超参数调整。即：总数据集划分为训练集、验证集和测试集。显然，模型总共经过k次训练和k次验证，基于k次训练的平均结果进行超参数调整并取最优参数组合作为最终模型的参数。此过程即为包含了“k折交叉验证法”的三步评估过程[26]。本文中取k=5。

3.2 参数优化

机器学习模型的参数取值直接影响到模型最终的表现性能，而机器学习算法中需要优化的参数较多，手动进行调整过于繁琐。常用的自动参数优化方法包括网格搜索法、随机搜索法、自助抽样等。本文采用网格搜索法进行参数优化，即：人为给定参数搜索范围并进行遍历搜索，选取最优的参数组合。4种机器学习模型具体的超参数搜索空间如表2所示。

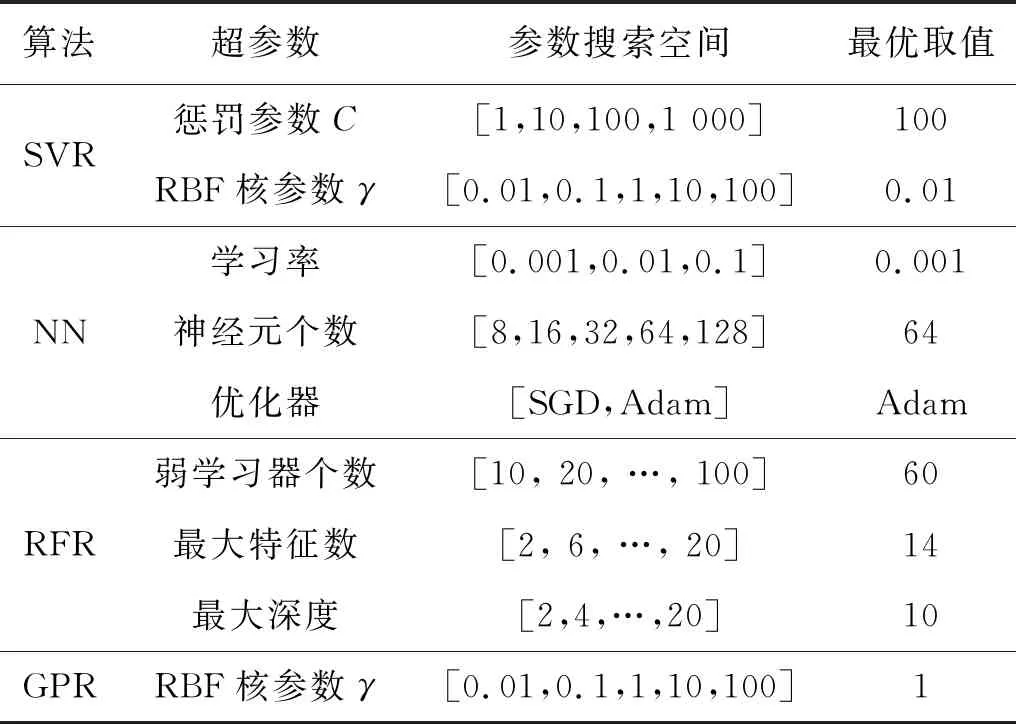
表2 超参数搜索空间

4 预测结果

4.1 评价指标

为了对4种算法的预测性能进行评估和对比，使用平均相对误差(average relative error, ARE)和最大相对误差(maximum relative error, MRE)2种评价指标，具体表达式如式(6)所示。

(6a)

(6b)

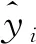
4.2 结果分析

基于Python平台，本文实现了以上4种机器学习算法并对测试集进行结果测试。测试集T的大小为23，记为T1～T23。图6和图7给出了不同机器学习算法在相同测试集上的预测结果。图8和图9给出了不同机器学习算法测试集上的平均相对误差(见式6(a))和最大相对误差(见式6(b))。

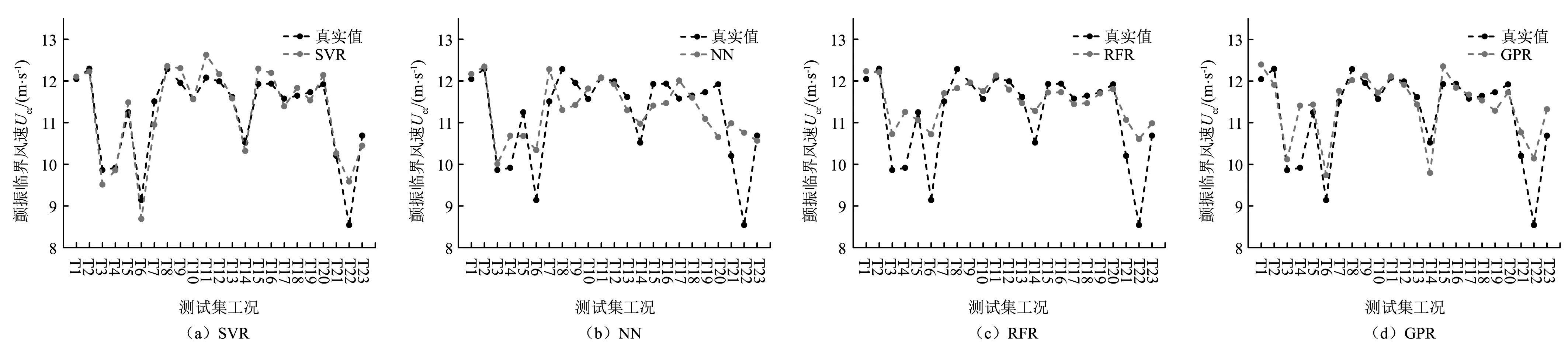
图6 不同机器学习算法施工态断面(Group1)预测结果

图7 不同机器学习算法成桥态断面(Group2)预测结果

从图6和图7可以看出，4种不同的机器学习算法在两组断面(施工态和成桥态)颤振临界风速的预测上整体表现性能较好。结合图8(a)和图9(a)来看，SVR在测试集上的预测ARE均最低(2.42%和5.43%)，而神经网络算法性能较差，ARE高达5.27%和13.84%。由图8(b)和图9(b)的MRE来看，误差趋势基本与图8(a)和图9(a)保持一致。

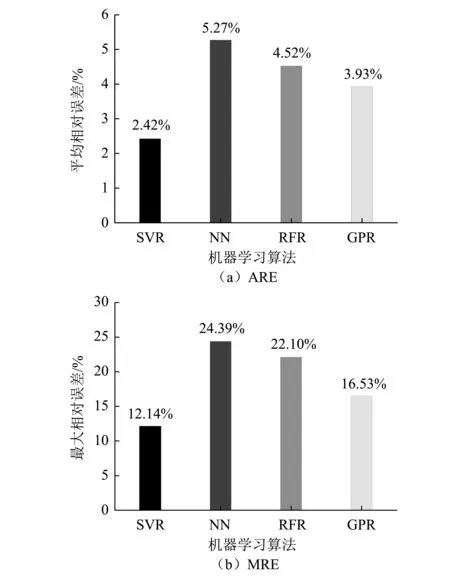
图8 施工态断面(Group1)预测结果相对误差

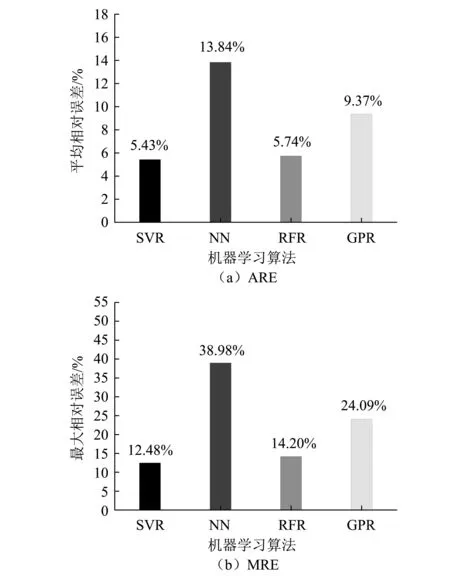
图9 成桥态断面(Group2)预测结果相对误差

经发现，以上4种算法最大误差基本都出现在FB2断面(斜腹板倾角21°)，且风攻角均为5°。探究其可能的原因有二：①大攻角引起的气动外形突变较大，由此导致的气动性能(颤振临界风速，施工态：8.54 m/s，成桥态: 4.71 m/s)与其他工况差异明显；②构建训练集所用的采样空间(即各个特征参数所覆盖的范围)不足以反映断面特性和动力参数与颤振临界风速之间的非线性映射关系，即存在局部变异点，进而导致机器学习算法无法深度感知该工况的特性。

总而言之，以上机器学习算法在两组断面(施工态和成桥态)的数据集学习结果均表现良好，尤其是SVR算法。对于其他3种算法而言，尽管预测精度不如SVR，但均在施工态断面(Group1)上有较好的表现性能。

4.3 对比研究

为了进一步展示机器学习算法在流线型箱梁颤振性能评估上的优越性，以下对比了JTG/T 3360-01—2018《公路桥梁抗风设计规范》中给出的3种不同颤振临界风速评估简化公式计算结果，包括Van der Put公式，Selberg公式和项海帆公式，如下所示

(7a)

(7b)

(7c)

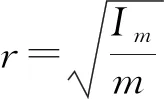
利用测试集中不同工况的动力参数，基于以上式(6)，可计算出测试集中对应工况0°±3°攻角下的颤振临界风速，并基于此得到颤振临界风速的平均相对误差。表3给出了3种颤振临界风速评估公式计算测试集工况所得的结果。

表3 规范中颤振评估公式计算结果平均相对误差

以上结果可以看出：3种不同的颤振临界风速计算公式预测结果较为一般，Van der Put公式计算Group1的结果平均相对误差最小，为16.08%；对于Group2，项海帆公式计算的结果平均年相对误差最小，为22.24%。显然，简化计算公式的结果与本文基于机器学习算法的预测结果相比，仍存在不小的差距。

为进一步验证本文提出的方法在实际桥梁上的表现性能，本文搜集了部分已建成桥梁成桥态断面风洞试验测得的颤振临界风速结果，并基于其断面尺寸和动力参数，利用本文提出的SVR算法进行预测。表4给出了4座已建成桥梁在3个不同风攻角下的颤振临界风速预测结果的平均相对误差。从表中可以看出，0°攻角下的颤振临界风速预测精度较高，均在4%以下；而对于±3°而言，其误差均在6%以下(仅苏通大桥超过6%，为6.02%)。由此可以说明：本文基于SVR的快速预测颤振临界风速算法具有较高的预测精度，可推广应用于实际桥梁颤振临界风速预估。

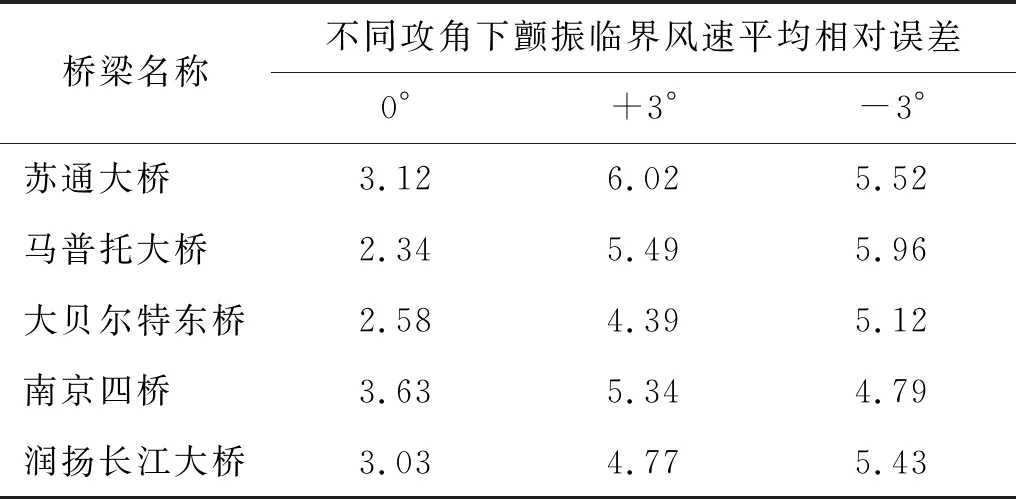
表4 SVR预测已建桥梁颤振临界风速的平均相对误差

至此可以看出，机器学习算法可以非常有效地预测不同流线型箱梁断面的颤振临界风速，且以支持向量机回归最佳。该算法相对于规范提出的简化计算公式而言，精度有较大幅度的提升，且在实际桥梁断面上表现性能较好。值得一提的是：本文训练模型的数据集大小仅为75，若能够收集到更多的以建或在建桥梁风洞试验结果并进行模型训练，该机器学习策略将可以有效地预测不同断面的颤振性能，进而可以提供桥梁设计者较高精度的流线型箱梁断面气动性能评估结果。

值得一提的是，本文所选取的流线型箱梁断面只包含施工态和设置了栏杆的成桥态，均未设置其他诸如检修车轨道、中央稳定板等附属设施，且未考虑栏杆透风率、检修车轨道高度、中央稳定板高度等因素的影响。文献[27-28]：以上措施会对流线型箱梁气动性能产生较大的影响。显然，增加以上输入特征维度将可以全面地考虑附属设施对颤振临界风速的影响。进一步地，机器学习方法可拓展到涡振响应预测、抖振响应预测等典型桥梁风致振动问题当中。这也是此类智能算法的优势所在。

5 结 论

本文基于4种机器学习算法(SVR，NN，RFR，GPR)，提出了快速预测流线型箱梁断面颤振临界风速的智能化策略。

(1)设计了预测流线型箱梁颤振临界风速的4种不同机器学习算法、训练方法及参数调优方法，基于风洞试验测得的两组断面颤振临界风速作为训练数据集，在测试集上的预测结果表明支持向量机算法在流线型箱梁断面颤振临界风速预测的问题上表现最优(平均相对误差施工态为2.42%，成桥态为5.43%)，神经网络模型最差(5.27%和13.84%)，其余2种方法次之，且平均相对误差均在5%和10%以下。

(2)对比公路桥梁抗风设计规范提供的3种快速计算颤振临界风速的简化公式计算结果和已建桥梁风洞试验结果可以发现，本文提供的机器学习方法精度远超过规范计算结果，且在实际桥梁上表现性能较好。

(3)作为基于数据驱动的预测方法，数据集的大小是提高机器学习方法精度的关键，未来可考虑扩展训练集并全面考虑诸如栏杆、导流板等附属结构对气动外形的影响，以达到更高精度的预测效果，进而满足工程设计需求并推广至工程应用。

(4)机器学习方法在诸多复杂非线性问题上的解决能力是较优的，但本文在算法实现过程中发现：建立良好的预测模型仍然需要注意模型类型的选取、数据集的质量、模型超参数的选取等问题。另外，机器学习方法属于“黑箱模型”，目前仍缺乏可解释性，且特征参数的选取较为依赖先验知识的干涉，这在推广机器学习算法至桥梁风工程领域时需要格外注意。