一种小型流体阻尼隔振器的设计与实验
2021-07-22黄子祥杨德权蒋圣鹏张志谊
黄子祥, 杨德权, 蒋圣鹏, 张志谊
(1.上海交通大学 振动、冲击、噪声研究所,上海 200240;2. 上海交通大学 机械系统与振动国家重点实验室,上海 200240)
惯性导航系统是一种利用陀螺和加速度计作为敏感测量元件的自主式导航系统[1]。系统本身具有高振动敏感性,并对安装空间和重量要求严格。设计一种小型轻量化被动隔振器,隔离对惯导系统等敏感元件的有害振动,具有较为重要的研究价值。这种被动隔振设计的本质是刚度系数和阻尼系数的设计[2]。
常见的弹性元件包括金属弹簧、波纹管、橡胶等,其中金属弹簧阻尼小,橡胶易受温度影响变性老化,而波纹管既可提供刚度,又可作为流体容器,广泛用于流体阻尼隔振器设计。如Honeywell公司为Hubble太空望远镜研发了一种波纹管型流体阻尼隔振器[3-4]。谢溪凌等[5]设计了以成型波纹管作为弹性元件的被动式隔振器,对于影响隔振性能的因素进行深入的实验分析。但这种波纹管型隔振器侧重于低频振动隔离,波纹管刚度不会太大,系统共振频率一般低于20 Hz。为获得较高的隔振频率,考虑到金属膜片刚度大的特点,可将其作为隔振元件使用。杨剑锋等[6]针对空间光学载荷在轨隔振问题,设计一种双层弹簧片隔振器,依靠中间层阻尼材料提供阻尼系数。陈涛等[7]采用冲压膜片设计了用于搭载光学遥感器的空间隔振器。朱海雄等[8]将带有周向交错条形孔的金属膜片,与下层的质量块、橡胶串联,构成双层隔振系统。值得注意的是,以上研究侧重于膜片式弹簧的应用,并未进一步分析膜片的弹性变形机理和尺寸参数的确定方法。
对于阻尼耗能,采用黏性流体产生阻尼的方式已经得到广泛应用。流体流动过程中的分子内摩擦及其与固体容器表面摩擦产生能量损失,在适当的温度和频率范围内,具有很强的耗能能力[9]。流体阻尼有两种主要工作方式:一种是间隙式流动,通过流体流经微小间隙时产生黏滞摩擦;另一种则是通过小孔节流作用实现耗能[10]。人们基于这两种流体阻尼结构,设计了各式流体阻尼器。早期是通过平行板间的相对运动产生阻尼,如Miyazaki等[11]为建筑物抗震设计的一种大型的黏滞阻尼墙结构。这种平行间隙的阻尼结构体积大,且阻尼效果较差。后来普遍采用在活塞上开设细长阻尼孔或环形间隙的方式来增强阻尼效果,目前的研究重点在于阻尼模型的建立。陈威[12]基于数值仿真,在相同过流面积条件下,比较孔隙式和间隙式阻尼器的阻尼力大小,结果表明间隙式阻尼器的输出阻尼力最大。而对于流体阻尼介质,目前工程应用上普遍采用硅胶和硅油。硅胶常作为一次性减振阻尼器的填充材料,由于导热性和黏温特性差的原因,不适宜长期使用[13]。对于温度、环境耐受性较强的硅油材料被逐渐应用到流体阻尼器的设计当中[14]。
本文研究一种以金属膜片作为弹性元件、由黏性流体间隙耗能产生阻尼的隔振器。其中膜片的有效直径较小,可提供105N/m量级的刚度,以实现高共振频率。为在高频共振条件下仍具备足够的阻尼比,以明显抑制共振,采用小间隙活塞式流体阻尼结构,性质稳定的二甲基硅油作为工作介质,为系统提供优良的阻尼耗能效果。采用薄板弹性力学理论分析金属膜片的受力变形。并通过隔振器动力学模型的建立,探讨隔振器的隔振效果和参数依赖性,力求隔振器尺寸尽量小、重量尽量轻。最后,通过实验模型验证隔振系统的振动传递特性。为高敏感器件提供一种结构紧凑、共振抑制显著的隔振方案。
1 隔振器结构
流体阻尼隔振器的基本构型如图1所示。采用环形金属膜片作为弹性元件,膜片中心与下端活塞固连。当上端连接杆位置垂向受力时,膜片发生法向弯曲变形,带动活塞做轴向运动。不妨将活塞的上、下端腔室分别称为上腔和下腔。当活塞下行时,上腔体积增大,下腔体积减小,下腔的流体受压,并通过活塞与壳体间的环形缝隙流入上腔,从而产生阻尼耗能效果。
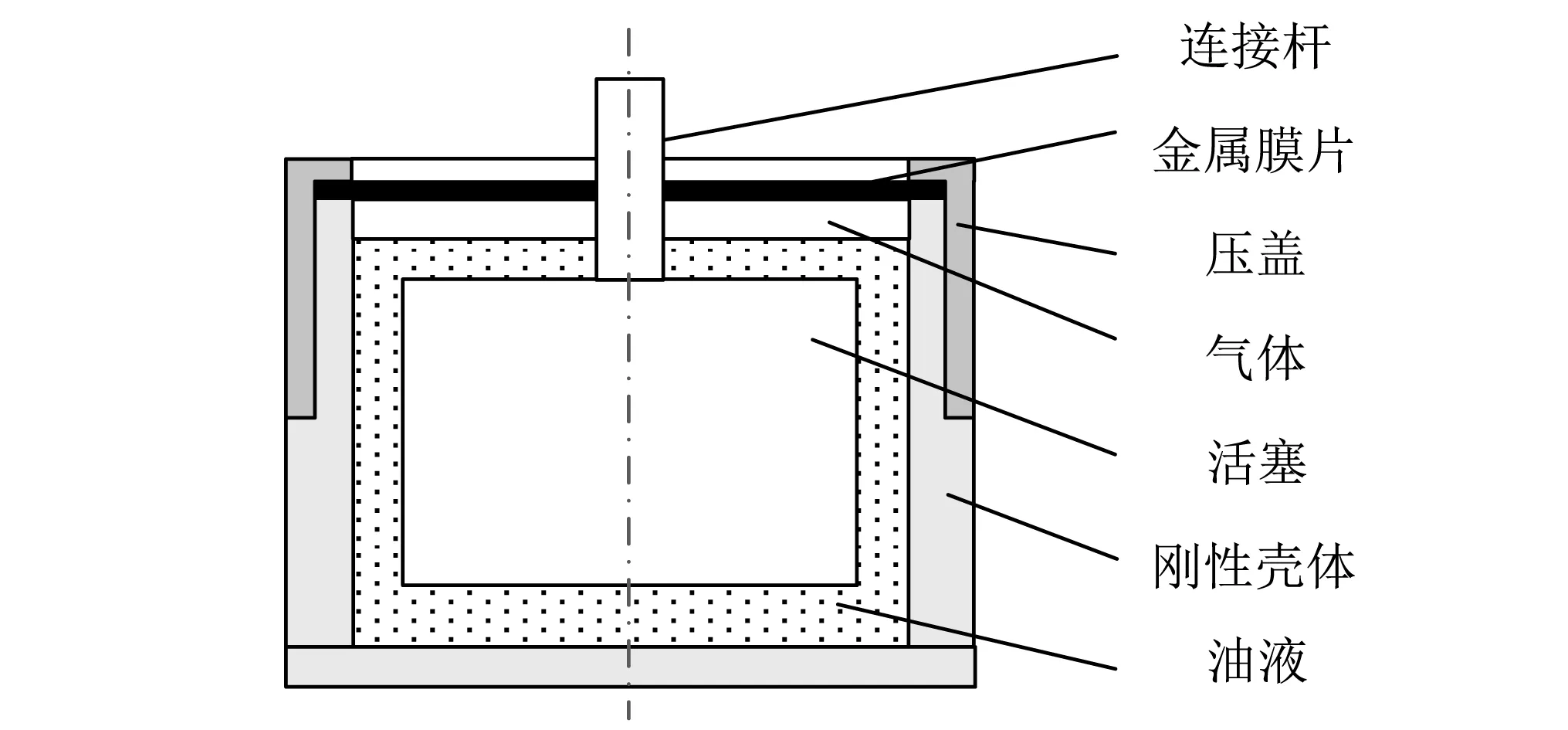
图1 隔振器结构示意图
注意到隔振器上腔留有一段空气。倘若完全充满油液,上腔体积变化量难以完全填满油液的流入量,膜片要发生相当程度的形变,刚度会过大。所以用体积模量较小的空气,来补偿上腔的体积变化。
隔振器的设计参数如下:隔振器高度<25 mm,直径<33 mm,质量<50 g。四个隔振器并联工作,负载质量为4 kg,安装频率约120 Hz,共振放大因子<6 dB,400 Hz处传递率<-12 dB。根据以上尺寸、重量及隔振性能要求,进行隔振器参数设计。金属膜片有效外径为18 mm,活塞长度为10 mm,二者受隔振器外形尺寸约束。而膜片的有效内径、厚度则根据安装频率确定。气腔高度不宜过小,此处高为1 mm,避免产生较大的附加刚度。为有效抑制共振放大因子,阻尼应尽量大,因此环形间隙宽度应尽量小(缩减至0.6 mm)。采用二甲基硅油作为流体介质,根据所需阻尼系数大小确定黏度。主要受力构件连接杆为不锈钢、膜片采用65Mn弹簧钢,其余构件材料均选用7072铝合金,使整体质量降至36 g。
2 隔振器动力学分析及运动传递特性
2.1 金属膜片法向弹性变形
金属膜片的内圆孔刚性固定在连接杆上,外圆由压盖拧紧固定。可将其简化成刚性圆与弹性圆环的组合,弹性圆外圆周固支,如图2所示的圆形薄板模型。其中交界圆半径为b,整体外半径为a,厚度为t。
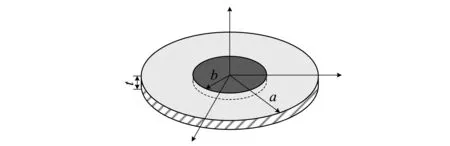
图2 复合圆板
只考虑法向振动的情况,由于形状、载荷及边界条件呈中心轴对称,圆板微元受力为图3所示。
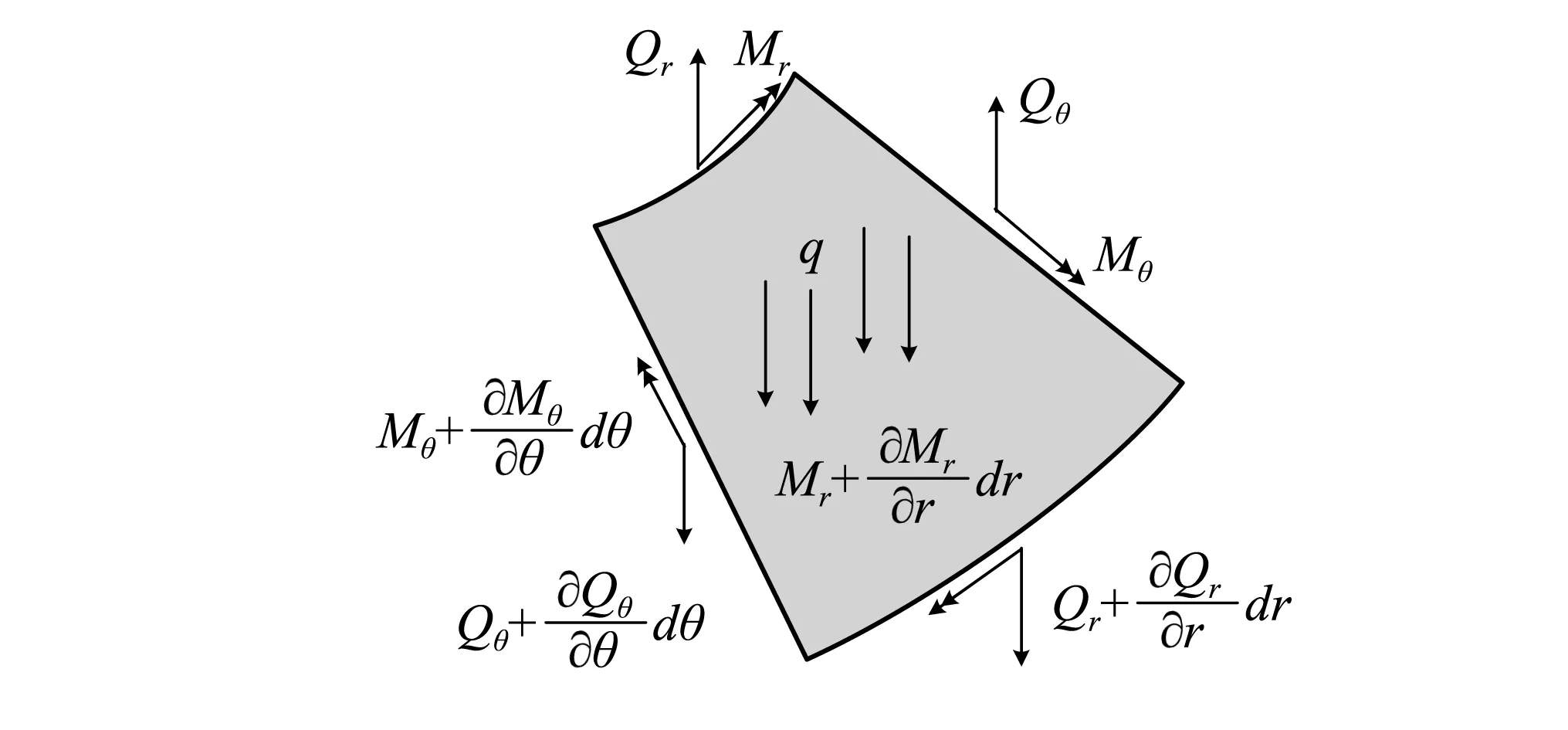
图3 微元体受力分析
图3中,Qr与Qθ,Mr与Mθ分别为作用在中面上的单位长度剪力和弯矩[15]。由微元的受力平衡可得出如下弹性薄板微分方程
(1)
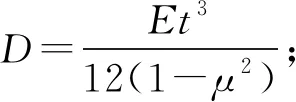
w=w0+w1=C1lnk+C2k2lnk+C3k2+C4+w1
(2)
式中:通解w0包含4个未知参数,可由边界条件得出;特解w1通常根据载荷q的作用形式得出。
当圆板传递法向振动时,主要有两种载荷作用形式。一种是等效到中心刚性圆上的垂向力F,一种是流体对弹性圆环的均布压力p,如图4所示。

图4 两种载荷作用形式
对于图4(a)的受力模型,由于结构的对称性,垂向力F与圆板弹性区任一圆周上的剪力Qr满足
(3)
式中,Qr有如下解析式
(4)
考虑到图4(a)无面力作用,可设通解w1=0,边界条件为
(5)
由此可得待定系数为
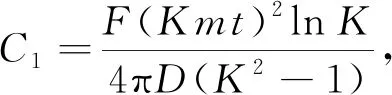
(6)
对于图4(b),载荷沿径向均布,取特解为w1=ηr4,代入式(1)解得η=p/(64D);边界条件为
(7)
由此解得待定系数为
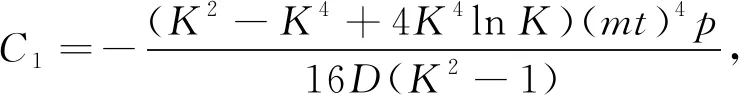
(8)
以上两组系数求取后,代入式(2)可得集中力作用下、均布压力作用下的金属膜片弹性变形表达式。这些推导的主要目的是,在2.2节中计算隔振器上腔的体积变化量和活塞下行量。
2.2 隔振器等效刚度和阻尼
如图5所示,将作用于隔振器连接杆端部的激振力简化为集中力F,活塞受力下行,膜片发生弯曲,活塞的位移量δ与膜片刚性区的下行量相等。下腔油液受压流入上腔,记下、上腔产生的压强为p1,p2。
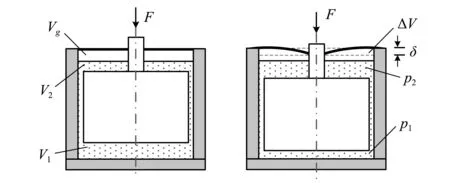
图5 隔振器受力变形
分别设上腔体积变化量为ΔV,流入上腔的流体体积为ΔVl,ΔVg为上腔空气受压缩的体积。假定流体不可压缩,且气液不互溶,则满足以下关系
ΔV=ΔVt-ΔVg
(9)
式中,ΔVl数值上等于环形间隙的油液流量Q的积分。
根据Streeter[16]的研究,与两侧压差有关,即
(10)
式中:vd为流体动力黏度;la为环形间隙的长度;h为环形间隙的厚度。将(p1-p2)前的系数项简记为λ,则有
(11)
气体压缩量则由体积模量定义
(12)
如图6所示,将活塞、连接杆的载荷等效移置到金属膜片上,则膜片的具体受力情况为:①膜片上方,刚性圆受集中力F;②膜片下方,刚性圆受等效集中力p1Acl-p2Acu,其中Acl为活塞下端面面积,Acu为活塞上端面与油液接触部分的面积;③膜片下方,弹性圆环面受均布载荷p2。
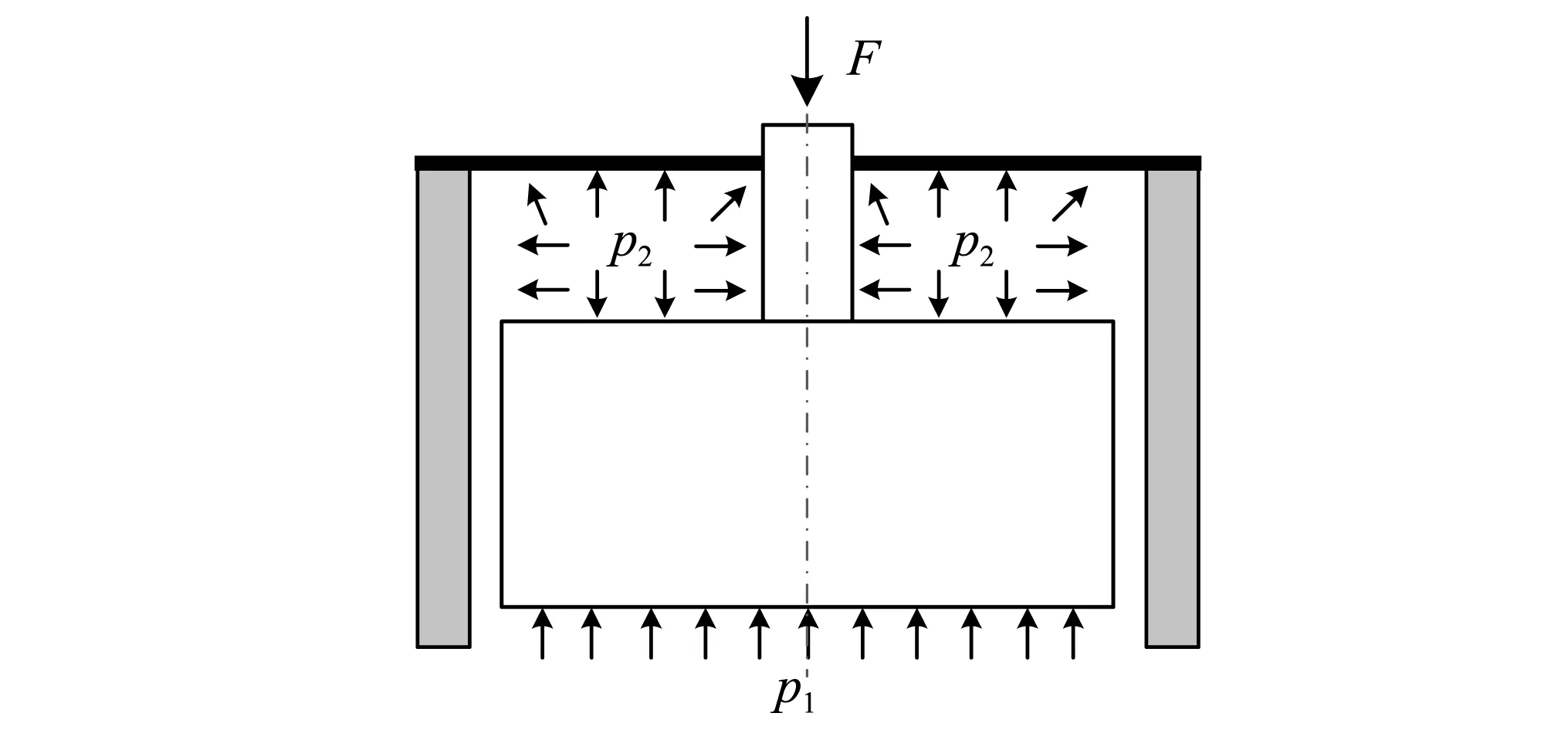
图6 隔振器内部受力示意
这里用到2.1节推导的挠度表达式。膜片变形可视为三种等效载荷①,②,③作用下的线性叠加,并可表示为腔内压力p1,p2与力F的线性组合,记为
ω(k)=∑ωi=λ1(k)P1+λ2(k)P2+λ3(k)F
(13)
特别地,将活塞的位移量δ表示为
δ=ω(K)=G1p1+G2p2+G3F
(14)
则上腔的体积变化量ΔV可积分得出
(15)
注意到ΔVl在数值上等于下腔体积的减少量,即
ΔVl=Aclδ
(16)
将式(12)~式(16)代入式(9)中,整理得如下关系式
H1p1+H2p2+H3F+H4δ=0
(17)
上述G1~G3,H1~H4与膜片参数有关。由于油液的不可压缩性,下腔油液的减少量等于上腔油液的增加量。联立式(11)与式(16),做拉氏变换,可得
Aclδs=λ(p1-p2)
(18)
联立式(14)、式(17)、式(18),消去p1,p2两个未知量,得到关于力F与其作用点变形量δ的关系式
(19)
整理得到隔振器动刚度表达式如下,其中常数项为等效刚度系数,s前的系数项为等效阻尼系数。
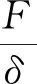
(20)
由式(20)可知,此构型的隔振器本质上是弹簧元件和阻尼元件并联的两参数模型。因此,可根据两参数模型的隔振特性设计隔振器参数。
2.3 两参数隔振模型的传递率特性
对于被动隔振器设计,常根据给定的隔振性能指标确定相应的隔振器设计参数。基于2.2节所得结论,不妨讨论刚度-阻尼并联的两参数系统振动传递特性。将传递率表达式记为
(21)
传递率极值对应为共振峰,则峰值频率比可通过求取极值点获得,令dT/dr=0,解得峰值频率比为
(22)
峰值频率要求为ωe附近,则有
(23)
共振放大倍数为
(24)
为使共振放大倍数不超过指定的Tlim,代入解得
(25)
若负载质量m给定,由式(23)、式(25)可获得符合要求的刚度系数km、阻尼系数cm。对于本文的研究对象,ζm=0.298 9,km=656 434 N/m,cm=484 N·s/m;在400 Hz处,传递率为0.238 9(<-12 dB)。
2.4 隔振器刚度和阻尼系数的影响因素
与刚度和阻尼系数相关的隔振器设计变量主要包含7个独立参数,即膜片有效外半径a、有效内半径b及膜片厚度t,环形间隙长度la、间隙宽度h,上腔气体体积Vg以及油液黏度vd。隔振器的设计参数选取在第1章中已有介绍,注意已选取参数应使算得的等效刚度ke与等效阻尼系数ce,尽量接近于2.3节中的两参数系统刚度、阻尼系数阈值km,cm。
下面讨论这部分参数的摄动对于等效刚度和阻尼的影响规律。将参数的变动率定义为:变动后的参数值与实际采用的参数值之比,如图7所示。
在图7(a)~图7(c)中,当金属膜片有效外半径a增大时,整体刚度下降,且由于环形间隙表面积增加,阻尼系数随之上升;而当膜片有效内半径b以及厚度t增大时,刚度增大明显,但不影响阻尼系数的大小。
在图7(d)、图7(e)中,隔振器刚度对于环形间隙长度la、间隙厚度h的变化不敏感。但阻尼系数受二者影响,与前者正相关,与后者呈负相关。
隔振器对于其他参数的敏感性见图7(f)、图7(g)。上腔空气体积Vg几乎不影响阻尼的大小,但当Vg较小时,刚度增大较为明显,这表明气体充足时,对刚度影响不大,但气体不够时,需要膜片产生很大的变形才能匹配下腔油液的体积变化。阻尼系数与油液黏度呈正比关系,而油液黏度对刚度几乎没有影响。
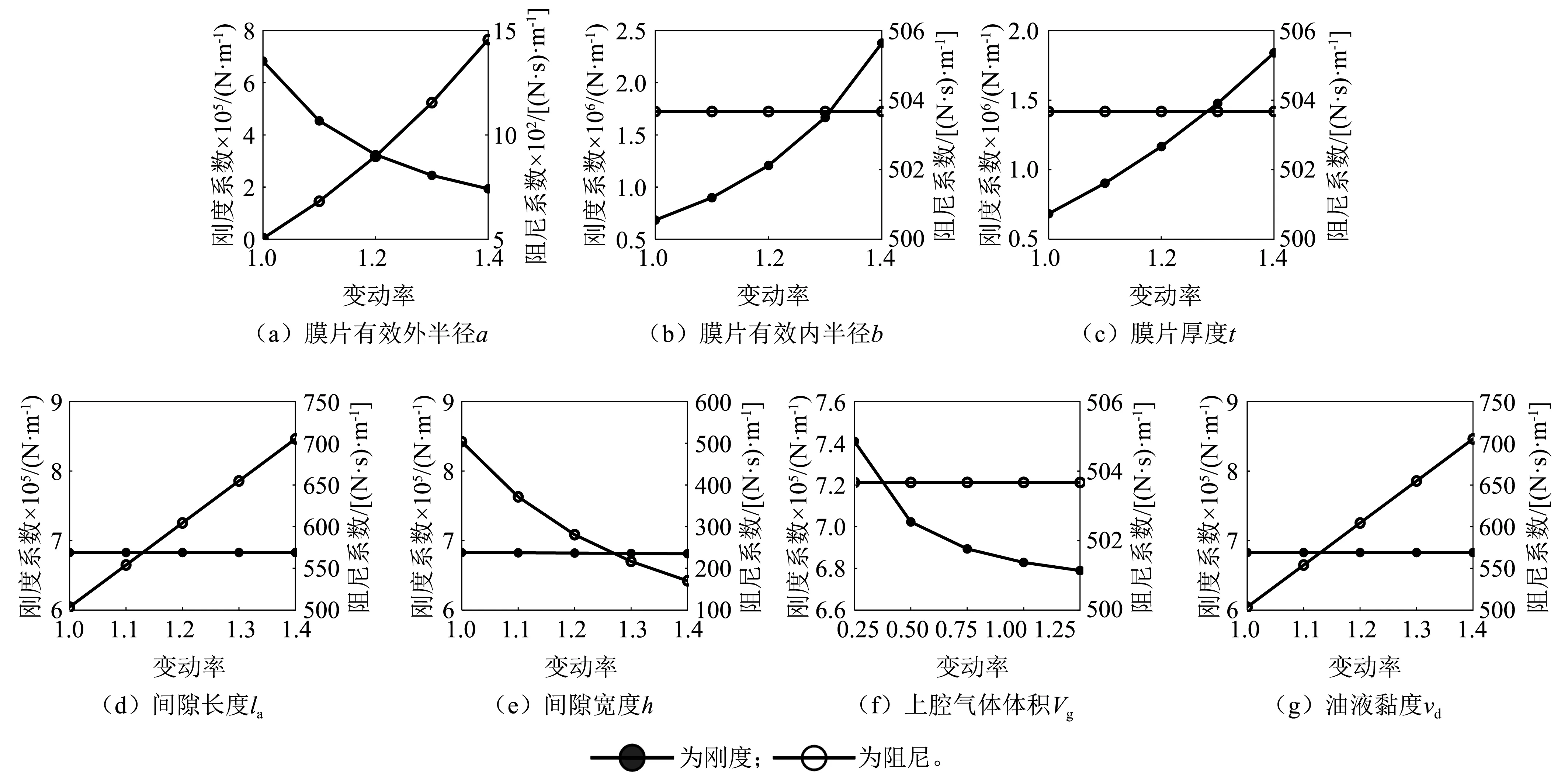
图7 隔振器参数变动对刚度及阻尼系数的影响
3 隔振系统振动传递特性测试
测试原理如图8所示,隔振系统包括4个流体阻尼隔振器和4 kg配重,用螺纹固定联接于振动台面上。布置单向加速度传感器1和2,分别测量振动台面和负载的加速度响应。通过外接的白噪声信号激励振动台产生垂向随机振动,激励频带为0~512 Hz,两个传感器测得的信号经计算机处理后得到频域的加速度传递率曲线。
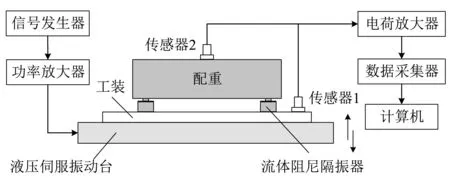
图8 隔振器测试原理图
对比理论计算曲线与实测曲线。二者的整体变化趋势吻合较好,如图9所示,但共振放大因子的理论值略小,表明阻尼系数的估算稍大。引起这一差异的原因可能是,在理论模型中,假定流速沿环形间隙轴向不发生变化,但流体存在出入口效应,实际上环形间隙的有效长度有所缩小。
在图9中,逐步增大油液黏度,阻尼系数提升,使得峰值频率略微减小,共振放大因子得到有效抑制,从21.6 dB降至5.9 dB。但阻尼系数的增加却拉高了曲线高频段,降低了高频区的隔振效果。因此,油液黏度不宜过大,才能兼顾共振峰的抑制与高频段的衰减。
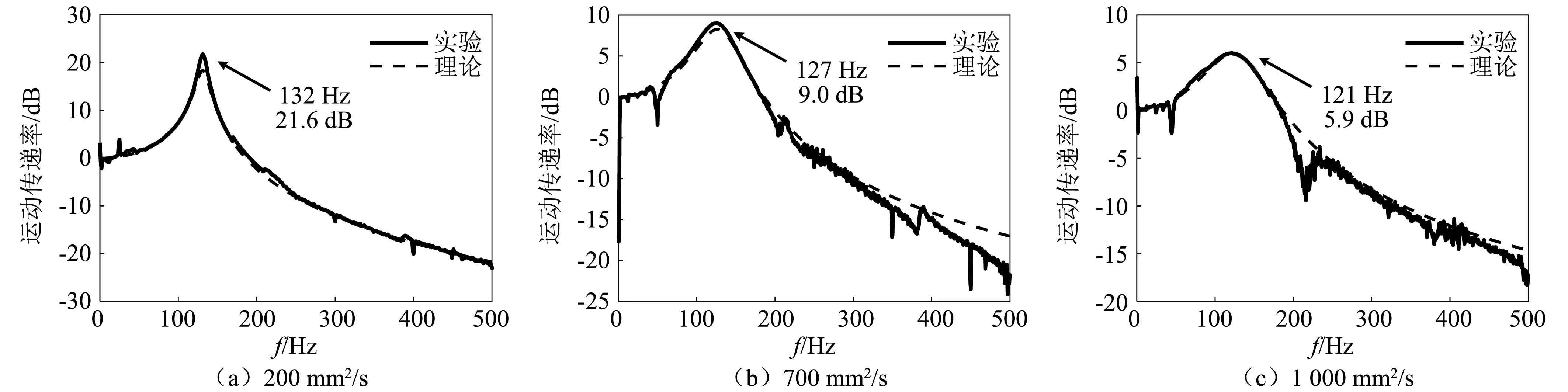
图9 运动传递率曲线
对于图9(c)1 000 mm2/s的传递率曲线,共振频率在120 Hz附近,且共振放大因子小于2,表明隔振器具有较大的阻尼。在220 Hz处出现较为明显的共振,该数值与振动台的固有频率接近。在400 Hz处高频衰减达到了-13 dB。满足对于隔振性能的要求。
4 结 论
将金属膜片结构与间隙式阻尼结构组合,设计的基于两参数模型的流体阻尼隔振器,满足小型轻量化要求,共振频率约120 Hz,共振放大因子约6 dB,400 Hz处衰减约-13 dB,共振抑制显著,高频衰减满足要求。文中提出的建模方法,可为黏滞流体阻尼隔振器设计提供参考。
