基于有限时间函数投影的电力系统混沌控制
2021-07-22张宏立
王 聪, 张宏立, 马 萍
(新疆大学 电气工程学院,乌鲁木齐 830047)
近年来,大规模的电网互联为电力生产和消费带来了极大的便利,但电力系统通常是由大规模的、地理位置分散的成百上千台发电机并行和同步运行组成,这些电机在大小和结构上各不相同,且涉及继电保护、自动装置、设施管理控制和时间调度装置等多种控制功能。因此,电力系统是一个典型的强耦合、高度非线性、多变量的动态系统,具有丰富的非线性动态特性,更易发生各类不稳定振荡行为。混沌行为作为其中一种复杂的动力学行为,会导致电力系统发生突发性的或情节严重的机电振荡,会导致系统大区域和大面积的停电事故,对电网的安全稳定运行造成了严重的危害。这些混沌振荡行为很难用传统的线性控制器来控制或抑制。因此,分析电力系统的混沌振荡机理,研究混沌振荡的有效控制方法是十分必要的。
电力系统的混沌振荡被认为是电压失稳的原因之一,为了有效地抑制电力系统的混沌行为,国内学者提出了大量的混沌抑制机制和方法。倪骏康等[1]研究了二阶电力系统的混沌动力学行为,并提出一种等效快速终端模糊滑模控制方法来实现混沌电力系统的稳定运行,该方法设计简单,减小了控制能量,降低了抖振;江世明等[2]针对互联二阶电力系统的混沌行为,基于非线性光滑函数,设计了一种新型滑模控制方法,该方法不需要被控对象的数学模型,且控制方法鲁棒性强;闵富红等[3]研究了施加功率扰动项的四阶电力系统的混沌动力学行为,并基于具有继电特性的切换函数设计了一种动态面滑模控制器,实现了混沌电力系统的快速控制;Luo[4]针对二阶电力系统发生混沌振荡的行为,基于无源控制理论设计了无源控制方法,设计自适应律使系统等效为无源系统,实现混沌控制,该方法对系统参数和外界扰动具有较好的鲁棒性;Ni等[5]研究了四阶电力系统的分岔及混沌行为,基于Lyapunuv稳定理论设计了一种简化控制器,该方法不仅简化了电力系统控制器的的设计,而且对系统参数的不确定性具有较强的鲁棒性;闵富红等[6]在2017年研究了含励磁环节的分数阶四阶电力系统的动力学行为,确定了系统产生混沌振荡的最低阶次,以及其他参数对系统动力学行为的影响,并基于分数阶系统稳定性理论和非线性反馈理论设计了同步控制器,有效的抑制了系统的混沌行为;Rajagopal等[7]推导了四阶分数阶电力系统的动力学模型,研究了其分岔及混沌行为,并提出一种自适应分数阶滑模控制混沌方法,有效地实现了混沌电力系统的控制;Karthikeyan等[8]研究了一类特定的智能电网的非线性行为,证明在一定条件下智能电网存在分岔及混沌行为,并基于滑模控制和PID(proportion integration differentiation)控制提出了混沌抑制方法;Min等[9]研究了受励磁限制影响的电力系统的混沌动力学行为,并设计一种新的自适应反推滑模控制器设计,用于消除差异的角度,使电力系统在稳定轨道上运行。
以上控制方法均在电力系统的分岔及混沌控制中取得了较好的效果,但以上控制方法均未考虑到实际工程需求,控制器设计较复杂或未考虑控制响应时间。研究电力系统的混沌行为,并且有针对性地提出相应的混沌控制策略,并考虑实际工程意义问题变得尤为重要。目前,利用有限时间稳定原理对系统进行控制的研究较多,但在电力系统的混沌控制中应用较少。Ni等[10]基于快速有限稳定性理论,提出了一种快速定时非奇异终端滑模控制方法,该方法能使混沌电力系统在有限的时间内实现稳定;同年,Ni等[11]针对三节点四阶电力系统的混沌行为,设计了一种固定时间的动态面高阶滑模控制方法,通过构造两个高阶滑模面并结合有限时间理论,实现了混沌控制;赵辉等[12-13]针对四阶电力系统的混沌振荡行为,基于有限时间稳定原理,分别设计了两种混沌控制器,有效的控制了电力系统的混沌振荡行为,并验证了所提方法的有效性和鲁棒性;刘利花等[14]证明了Watts-Strogatz 型小世界发电机网络的系统参数处于某些范围时,会出现混沌振荡,并基于反馈控制和有限时间稳定理论设计了有限时间控制器,实现了发电机网络的振荡控制。
为了提高电力系统的混沌控制效果,简化控制器的设计,缩短控制响应时间,本文提出了一种基于有限时间稳定理论和函数投影同步思想的混沌控制方法。借鉴混沌同步思想,并结合有限时间理论,将混沌电力系统与理想状态电力系统在有限时间内实现完全同步,间接实现电力系统的混沌控制。数学理论及仿真结果表明,该控制器能在有限时间内有效地实现了混沌电力系统的控制,且对外部干扰具有较强的鲁棒性。
1 理论基础
函数投影同步是将驱动系统和响应系统按照给定的尺度函数α(t)实现同步[15],给出如下的混沌系统
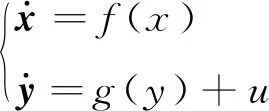
(1)
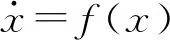
e=x-α(t)y
(2)
式中,α(t)为尺度函数。
假设1α(t)不等于0,且在[0,+∞]内连续,可导且有界。
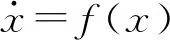
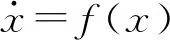
(3)
有限时间稳定理论指的是不稳定系统在短时间内被控制到稳定态[17]。有限时间稳定控制是一种能对非线性系统实现有效控制的方法,能使受控系统变量在有限时间内收敛到平衡点,而且控制器中含有分数幂项,这也大大增加了控制器的鲁棒性能和抗干扰性能。有限时间控制可以使函数投影误差系统在有限的时间内达到平衡点,不仅减少了控制响应时间,也更具有实际工程意义。
函数投影同步误差为
(4)
式中:ei(t)∈Rn投影同步误差的状态量;f:D→Rn是D~n维空间D⊆Rn中的一个连续函数,且初始f(0)=0。
定义2如果存在一个时间t*,使混沌电力系统和稳定运行电力系统的误差系统满足
lim‖ei(t)‖=lim‖xi(t)-α(t)yi(t)‖=0
(5)
‖ei(t)‖=0,t>t*,i=1,2,…,N
(6)
式中: ‖·‖为范数,则混沌电力系统与稳定电力系统在有限时间内实现了同步。
定理2若存在一个正定连续函数V(x)满足
(7)
式中:m>0;0<ξ<1是常数,则对于任意的初始时间,关于V(t)的如下不等式均成立
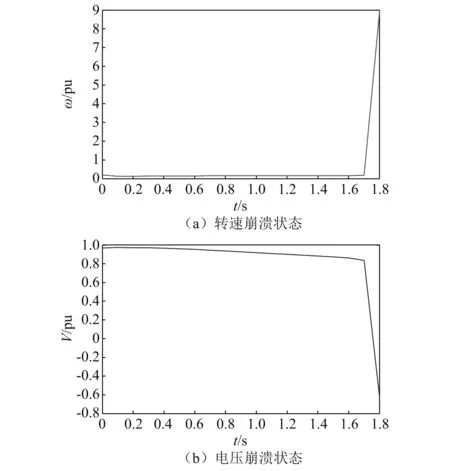
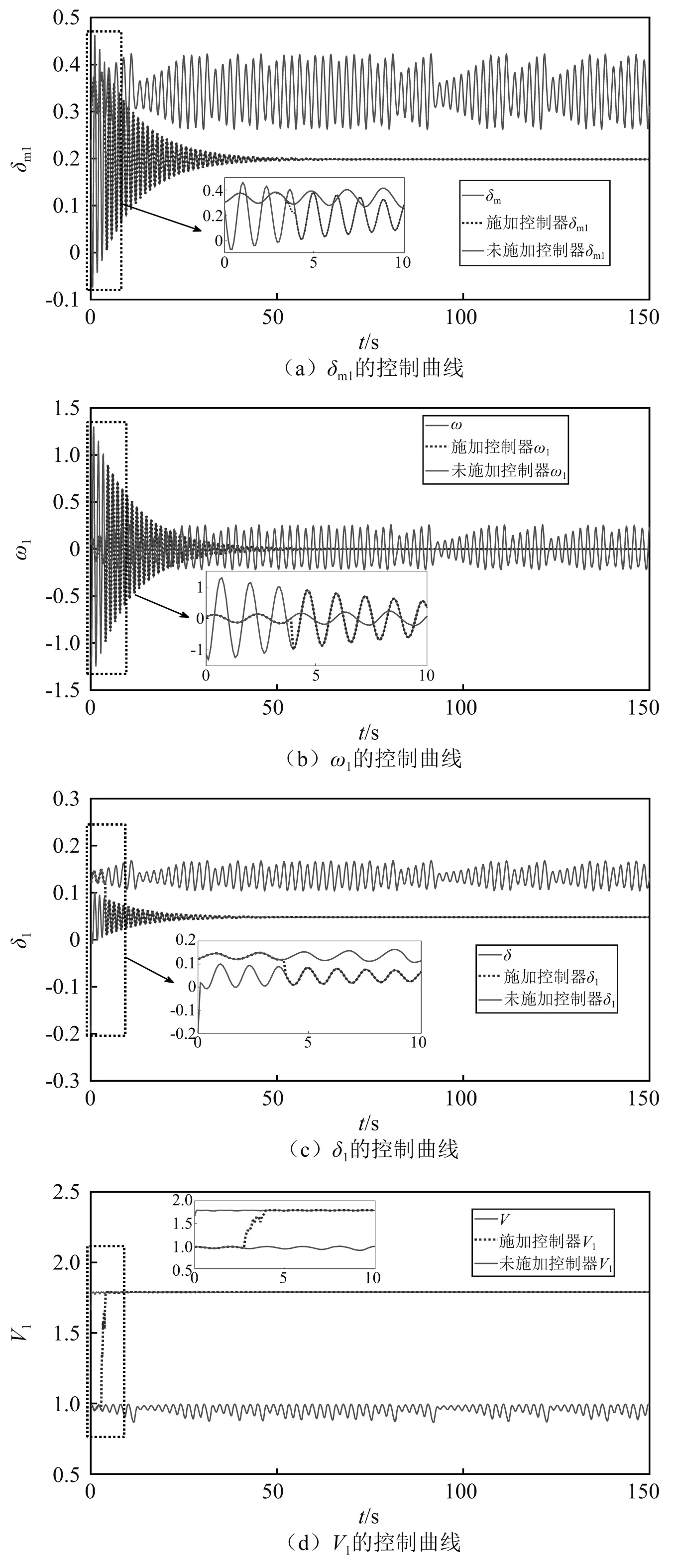
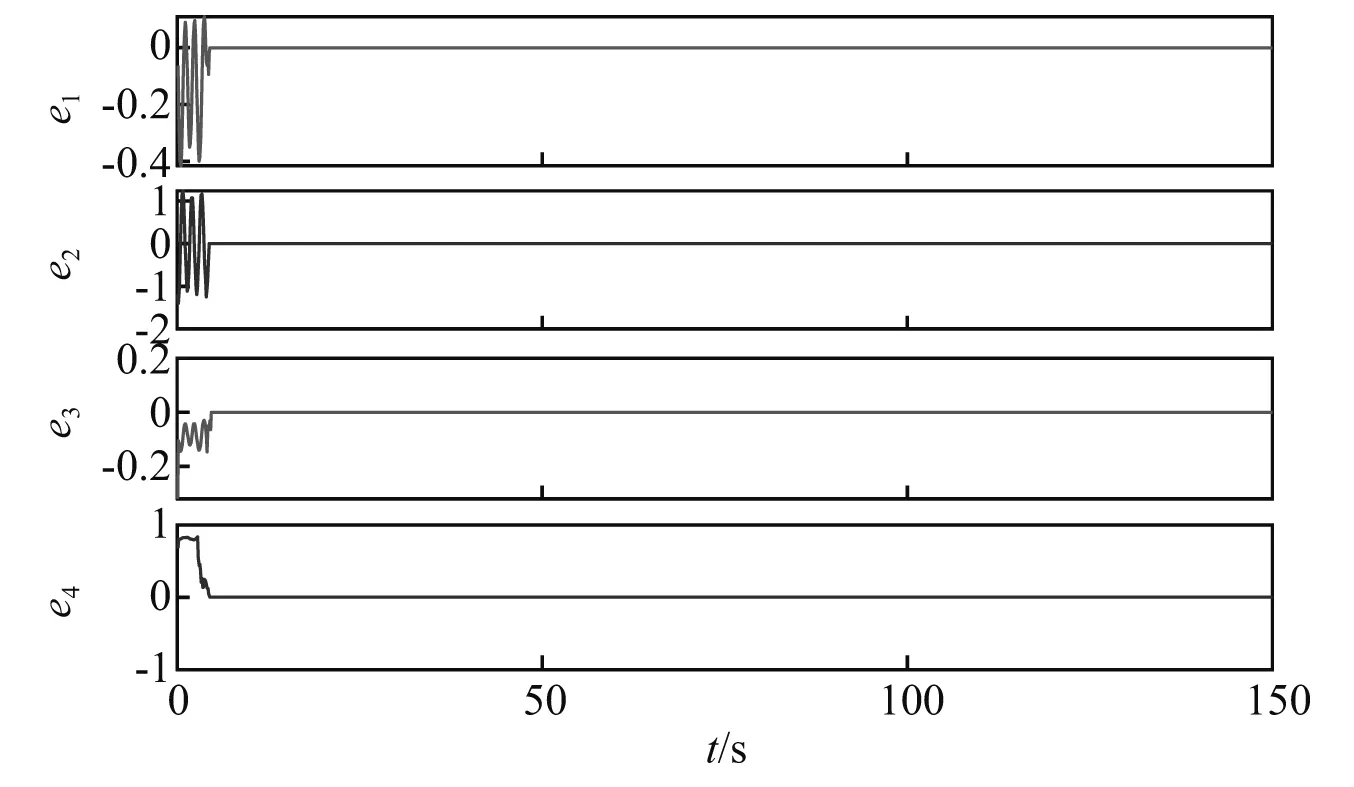
V1-ξ(t)≤V1-ξ(t0)-m(1-ξ)(t-t0),t0 (8) V(t)≡0, ∀t>t1 (9) 电力系统通常用包含系统参数的高维非线性动力方程组表示,本文以文献[18-19]提出的三节点四阶电力系统作为研究对象,系统模型如下 (10) 式中:δm为最大功率角;ω为转速;δ为功角;V为电压;Q1为系统的控制参数。 研究表明,对于四阶电力系统,随着控制参数Q1的变化,系统会经历倍周期分岔、霍夫分岔、鞍形分岔及混沌现象等,若参数变化到一定程度,则会出现电压和转速崩溃现象。当Q1=11.379时电力系统为混沌状态,其相轨迹图、状态变量时序图、庞加莱截面和功率谱图见图1。当Q1=11.4时系统电压崩溃,见图2。 由图1(a)和图1(b)可以看出,混沌运动的状态变量都处于不规则的周期混沌状态, 由图1(c)可以看出,庞加莱截面表面呈现密集的点且具有层次结构,映射的结果反映了电力系统的非线性混沌特征。混沌运动是有界非周期运动,由图1(d)可以看出,功率谱为连续谱该信号包含高直流分量和低频分量,功率谱出现宽带噪声,是典型的混沌行为特征。从图2可以看出,随着Q1的变化,电压幅值和转速变化缓慢,随着Q1时间变化,电压突然下降,发电机角速度突然上升,使电力系统处于崩溃状态。以上结果表明,在电力系统处于混沌状态时,系统电压、功角等均处于无规则的运动状态,严重威胁电网的稳定运行。 图1 Q1=11.379,电力系统为混沌状态 图2 Q1=11.4,系统崩溃状态时序图 有限时间函数投影控制是基于有限时间稳定理论和Lyapunov稳定理论,借鉴函数投影同步思想,提出的电力系统混沌控制方法。该方法通过设定理想运行状态的电力系统为驱动系统,混沌状态的电力系统为响应系统,并给定尺度函数,将混沌电力系统的控制问题转化为混沌系统的同步问题。针对同步误差设计控制器u,使驱动系统和响应系统的状态同步误差为0,即混沌电力系统在控制器u的作用下运行于稳定状态,同时结合有限时间理论,设计控制器u使响应系统和驱动系统满足在有限的时间内同步误差趋于0。 当Q1=11.379时系统为混沌状态,当Q1=0时系统运行在稳定状态,稳定运行时各个状态量随时间的变化曲线,如图3所示。 图3 稳定运行时各状态量随时间的变化曲线 选取当Q1=0时的电力系统作为驱动系统,如下 (11) 选取当Q1=11.379时,处于混沌运行状态的电力系统作为响应系统,如下 (12) 式中,u1,u2,u3和u4为待设计的控制器,则有限时间函数投影同步误差如下 (13) 式中,α(t)为尺度函数。对函数投影同步误差进行求导得 (14) 定理3对于混沌电力系统系统式(12),设计如下的控制器可使系统实现有限时间函数投影同步控制。 (15) 式中,0 证明:构造Lyapunov函数 (16) 对Lyapunov函数进行求导得 (17) 将式(11)、式(12)和式(13)代入式(17)得 (18) 又有 (19) 所以 (20) 由以上分析可知,混沌电力系统在控制器式(15)的作用下,可在有限时间内实现函数投影混沌控制。 仿真参数设置:选取驱动系统的初始条件为[δm(0),ω(0),δ(0),V(0)]=[0.3,0,0.2,0.97]; 响应系统的初始条件为[δm1(0),ω1(0),δ1(0),V1(0)]=[0.3,0,0.2,0.97], 尺度函数选择α(t)=sin(t)+2,E为0.5,仿真时间为150 s。 为了验证该方法的有效性,在3 s时投入同步控制器,图4给出了施加控制器后的各个状态变量随时间的变化曲线。 由图4可以看出,投入控制器后混沌电力系统的四个状态迅速响应,在极短的时间内与稳定电力系统的状态达到同步,运行于稳定运行状态。由图4(a)~图4(d)的控制曲线及对应的局部放大图可以看出,在投入同步控制器前,电力系统处于混沌运行状态,施加控制器后,施加控制器的混沌电力系统的系统状态迅速与稳定运行状态达到同步,混沌电力系统进入稳定运行状态,而未施加控制器的混沌电力系统,仍运行于混沌状态。 图4 施加控制器的混沌电力系统的时间序列图 图5给出了有限时间函数投影同步误差随时间变化曲线,由图5进一步可以看出,对响应系统施加控制器后,函数投影同步误差在极短的时间内即可达到0,表明混沌电力系统在投入控制器后能迅速的同步于稳定状态的电力系统,实现了混沌控制。 图5 误差随时间的变化曲线 为验证该控制方法的鲁棒性,对受控混沌电力系统施加干扰n(t)=0.001cos(0.2πt),将干扰施加到系统式(12)的第一个状态方程。选择在3 s时投入同步控制器,图6给出了有限时间函数投影同步误差随时间变化曲线,图7给出了施加控制器后的各个状态变量随时间的变化曲线。 图6 含外部扰动时误差随时间的变化曲线 由图6可以看出,对受到外部干扰的混沌电力系统施加控制器后,误差信号仍可经过短时间的振荡后衰减到零。由图7进一步可以看出,在有外部噪声干扰的情况下,施加控制器后,混沌电力系统的各状态仍能迅速的与理想状态达到同步。仿真结果表明,所设计的有限时间函数投影控制器对外界干扰具有较好的鲁棒性能。 图7 含外部扰动时施加控制器的混沌电力系统的时间序列图 有限时间函数投影同步是利用函数投影同步思想使混沌电力系统稳定运行于理想状态,又结合有限时间理论保证了控制响应时间。该方法结合了有限时间控制的快速性及函数投影同步控制的设计简单等优点,不仅具有很好的控制效果,缩短了控制器响应时间,提高了控制器的快速性,而且该方法不需要确定平衡状态,根据函数投影同步的思想仅需要选择合适的驱动系统,灵活性更强。 本文以四阶电力系统为研究对象,利用含有功率扰动项的四阶电力系统模型,通过绘制相图、状态序列图、庞加莱截面以及功率谱图研究了功率扰动项对系统运动状态的影响,验证了电力系统在一定条件下会发生混沌行为,且当扰动幅值达到某一值时会引起系统的电压崩溃。为了提高电力系统的混沌控制效果,简化控制器的设计,缩短控制响应时间,本文基于有限时间稳定理论和函数投影同步思想,设计了有限时间函数投影混沌控制器,将混沌电力系统与理想状态电力系统在有限时间内实现完全同步,间接的实现了电力系统的混沌控制。理论上证明了该控制器的正确性,数值仿真进一步验证了所设计控制器可快速、有效的实现电力系统的混沌控制,并验证了该控制器对外部干扰的强鲁棒性。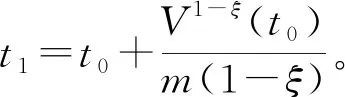
2 混沌电力系统

3 混沌电力系统有限时间函数投影同步控制
3.1 控制器设计及稳定性分析
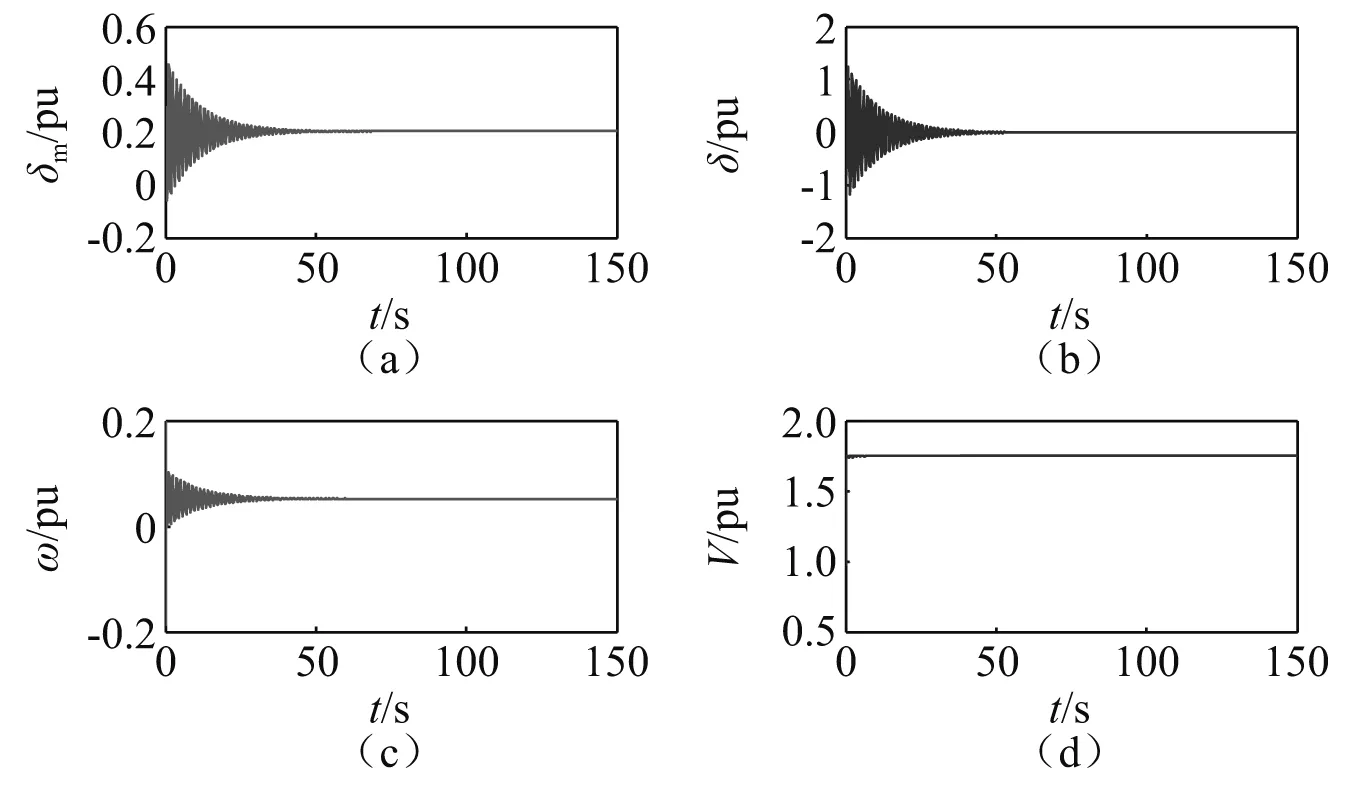

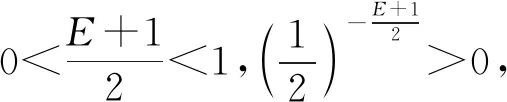
3.2 数值仿真

4 结 论
