侵彻条件下岩石类材料RHT模型参数敏感性分析

聂铮玥， 彭 永， 陈 荣， 蔡镇清， 李付刚

(国防科技大学 文理学院，长沙 410073)

RHT(Riedel-Hiermaier-Thoma)模型广泛应用于岩石、混凝土类材料在高应变率、大变形问题中的动态力学响应模拟[1]，国内外学者基于RHT模型开展的爆炸冲击、弹体侵彻等研究都取得了比较理想的结果[2-4]。目前多数研究的重点在于，针对混凝土材料，基于实验数据对部分参数或模型进行修正与改进[5-8]。然而，当RHT模型应用于岩石材料时，由于不同种类岩石间的力学性能差异明显，一般需通过理论分析与力学实验相结合的方法来确定模型参数，不宜直接采用某种特定岩石或混凝土材料的参考值[9]。此外，RHT模型参数多达34个，获得参数所需力学实验包括物理性质测定、静态力学及动态力学等多种类型，使得参数确定比较复杂。因此，对模型中参数进行敏感性分析，甄别敏感性较强的参数，可以优化模型参数确定方案，提高数值模拟的效率。

对于RHT模型参数敏感性的研究相对较少，李洪超等[10-11]采用LS-DYNA数值软件并通过正交试验的方法，模拟分析了RHT模型中的部分复杂参数对大理岩及红砂岩霍普金森杆(split Hopkinson pressure bar, SHPB)压缩实验应力-应变曲线结果的敏感性，通过极差分析，给出了影响明显的材料模型参数排序。该方法实验设计合理，且能够在全局上获得拟合SHPB冲击曲线的最佳解。但由于SHPB冲击曲线结果将受材料物理性质影响而具有一定离散性，且不同应变率条件下获得的SHPB冲击曲线也将不同，因此该方法有一定局限性。刘殿柱等[12]同样利用正交试验法，以侵彻深度为评价指标，利用Autodyn软件对弹丸侵彻混凝土问题进行了部分参数的敏感性分析。该方法简明直观，但根据侵彻深度变化趋势图对敏感性进行排序时，由于部分参数影响相对不显著，因此结果具有一定主观性。辛健[13]通过模拟TNT在土中的爆炸过程，采用单因素变量法，得到了以损伤面积为评价指标的参数敏感度结果。该方法简洁直观，但参数水平设置情况通常有限，且RHT模型中参数并非完全独立，因此分析结果可能存在一定误差。为客观评价模型参数的敏感性差异，需要对计算参数矩阵进行合理设计与分析。同时，上述研究结果表明，针对TNT爆炸、SHPB试验与侵彻问题，RHT模型材料参数的敏感性不同。因此，针对特定问题，需要进行相应的参数敏感性分析，不能直接采用其他物理问题的敏感性分析结果。

针对实心弹体中低速正侵彻单层半无限厚岩石靶体问题，本研究基于ISIGHT软件中的优化拉丁超立方设计 (optimal Latin hypercube design，Opt LHD)算法设计了参数试验矩阵，保证了设计矩阵具有较优的空间填充性。采用LS-DYNA软件对侵彻过程进行了大量数值模拟，获得了不同参数组合条件下的仿真结果。然后以弹体侵彻深度、弹体质量损失率及靶体损伤度为评价指标，分析了模型参数的交互效应及主效应。最后通过建立侵彻深度、弹体质量损失率及靶体损伤度与参数间的响应面模型，定量计算了RHT模型中参数的贡献率。

1 RHT模型简介及参数分类

1.1 RHT模型介绍

RHT模型由Riedel等[14]提出，可以反映材料的应变率效应、失效面及损伤演化等特点。RHT模型包括状态方程部分及本构方程部分，如图1所示。

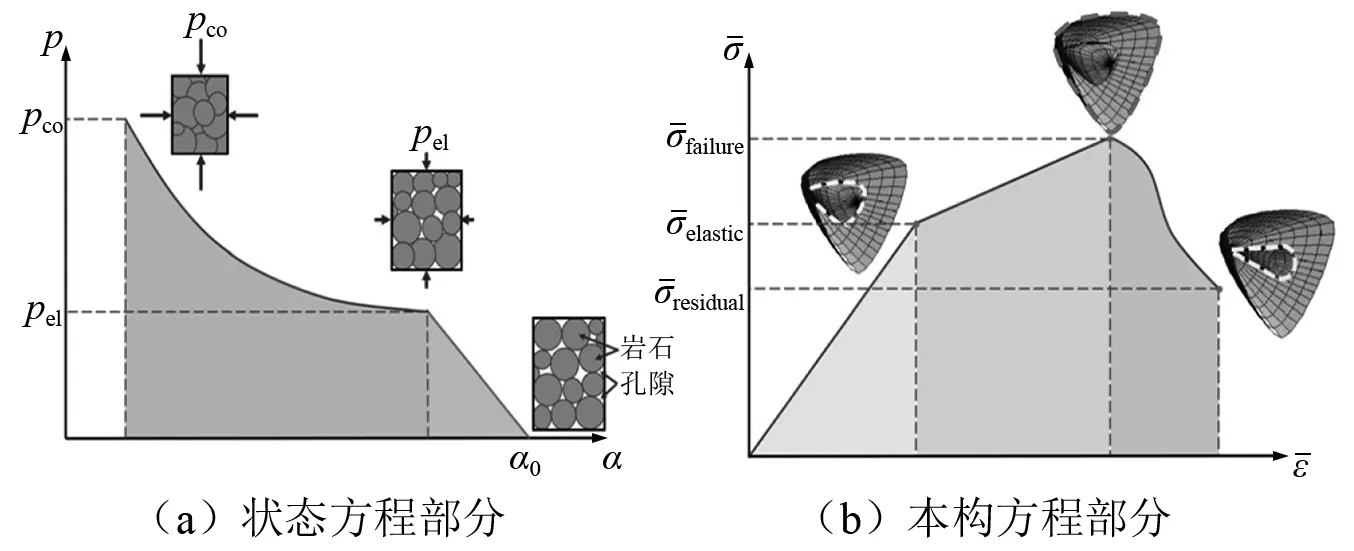
图1 RHT模型原理图

状态方程采用Herrmann[15]提出的P-α状态方程，以描述多孔及疏松介质中孔隙从压碎到压实的过程。本构模型由3个发展阶段组成，随着应力增加，材料首先经过弹性阶段到达弹性屈服面，此后材料发生塑性变形并进入线性强化阶段，材料表现出应变硬化特征，直至到达失效面。当等效应力强度超出失效应力强度后，材料开始出现累积损伤量，进入损伤软化阶段，最后到达残余强度面[14-16]。

根据RHT模型原理，基于参数物理意义，可对34个参数进行初步归类，如表1所示。

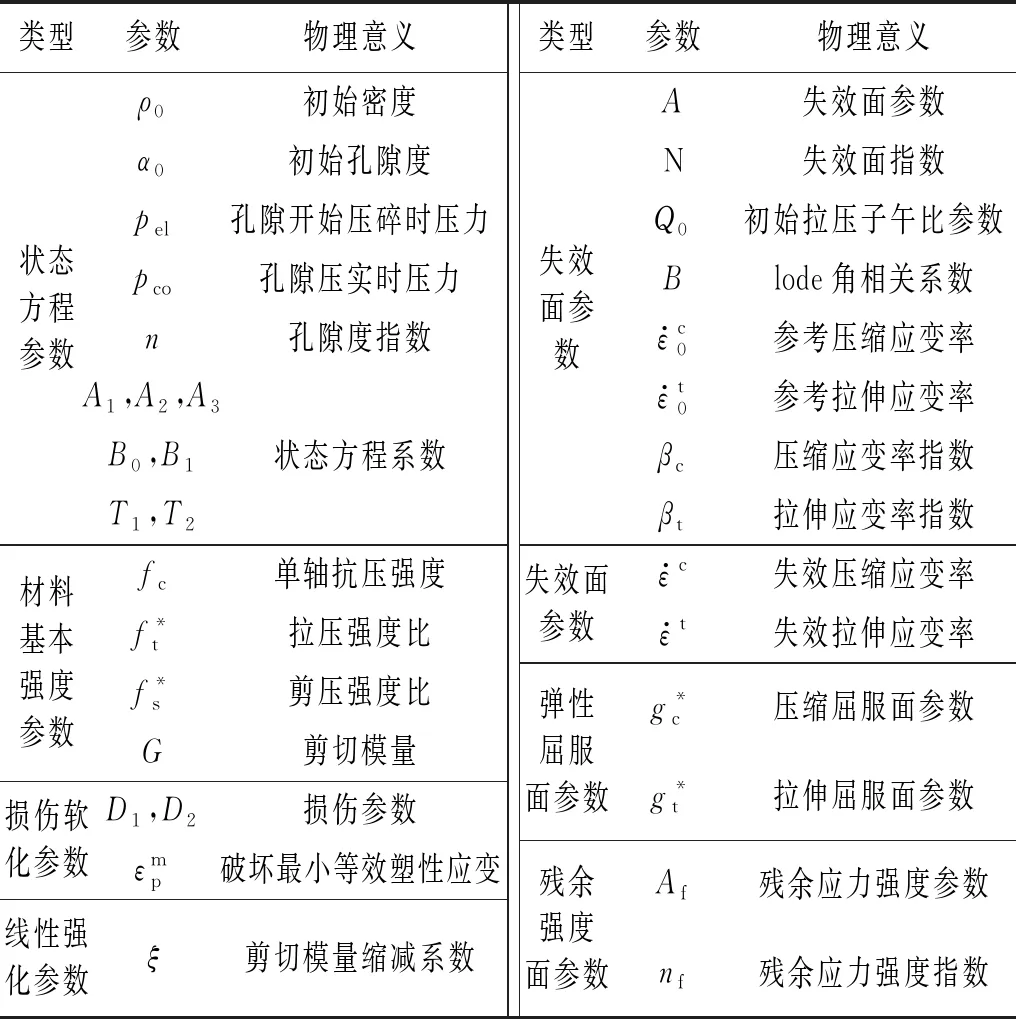
表1 RHT模型参数分类

1.2 参数分类及范围选取

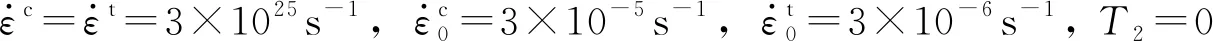
根据Rankine-Hugoniot方程及Mie-Grüneisen状态方程可以求得部分参数间关系为

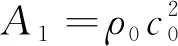
(1)

式中：c0为材料声速；s为材料参数，其值可以通过平板撞击试验中测定的材料冲击波速度和波后粒子速度结果线性拟合确定。其余参数间亦存在下列关系[17-18]

pel=fc/3
βc=4/(20+3fc)
βt=2/(20+fc)

(2)

因此，可将c0，s，fc作为主定参数，而A1，A2，A3，B0，B1，T1，pel，βc，βt作为其从属参数处理。综合各参数定义及式(1)、式(2)，主定参数、从属参数及定值参数的具体分类如表2所示，其中主定参数共计21个。

表2 主定参数、从属参数、定值参数分类

本研究针对岩石类材料，参考花岗岩、玄武岩、砂岩、千枚岩、大理岩、片麻岩共六种岩石的相关指标值[19]，确定了部分主定参数的取值范围。对于材料参数s的取值范围则根据岩石材料的平板撞击试验结果确定[20-23]。对于无法直接确定的其余主定参数，则利用C30/37混凝土RHT模型参数值作为基准值，并设置参数变化范围为基准值的-80%～80%。所有主定参数的取值范围如表3所示。

表3 主定参数参考取值范围

2 敏感性分析数值实验设计

2.1 参数矩阵设计

ISIGHT是一款可以灵活设计并调用各项软件进行计算，进而对结果进行后处理的计算机辅助优化软件[24]。本研究利用ISIGHT中的试验设计(design of experiments, DOE)功能，采用优化拉丁超立方设计算法(Opt LHD)进行参数矩阵设计，从而保证试验点具有较好的空间填充性及均匀度。

根据RHT模型中21个主定参数设计参数矩阵，为满足后续的交互效应及主效应分析，以及建立响应面模型的精度需求，参数水平个数的设计需满足最小采样点数。对于一阶、二阶响应面模型，其最小采样点数分别通过式(3)、式(4)计算

Smin,1=M+1

(3)

(4)

式中：Smin为最小采样点数；M为试验设计的主定参数个数。

因此，考虑到最小采样点数要求及计算成本，基于上节中的主定参数范围，利用Opt LHD算法设置了400个采样点，获得了图2所示的参数设计矩阵。

图2 主定参数设计矩阵

2.2 数值实验设计

利用LS-DYNA有限元软件对实心弹体中低速正侵彻半无限厚单层岩石靶体问题进行仿真。为节省计算时间，采用1/4对称模型进行仿真实验，尺寸及网格设计如图3所示，弹体在靶体中心处以600 m/s的初速度垂直向下侵彻。靶体的上表面设置为自由边界，下表面设置为无反射边界，以近似模拟半无限厚条件。

图3 模型尺寸及网格设计(mm)

弹体的材料选择为硬度较大的 30CrMnSiNi2A 钢，使用Johnson-Cook模型描述其材料力学性能，模型参数如表4所示。靶体材料采用RHT模型，其中主定参数为参数设计矩阵值，其余参数确定如1.2节所述。

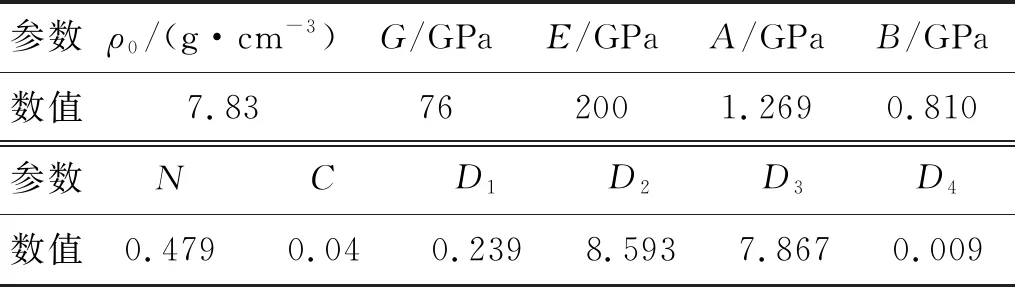
表4 弹体Johnson-cook模型参数[25]

3 RHT模型参数敏感性分析方法

为了定量描述参数敏感性大小以及参数变化对评价指标(即响应量)的影响规律，需对参数的交互效应、主效应以及参数对响应量的贡献率进行分析。参数的交互效应可以反映某一参数变化对响应量的贡献随其他参数的取值不同而发生变化的情况。参数交互效应显著则此时参数作用非独立。当交互效应不显著时，则通过参数主效应分析，可得到参数对响应量的影响规律。通过建立参数与响应量之间的近似模型，进一步计算各参数贡献率，评价参数的敏感性大小。

3.1 交互效应、主效应分析原理

参数交互效应及主效应的计算是先通过式(5)得到主定参数xi与响应量y之间多项式(以二次多项式为例)

(5)

式中：xixj为参数交互项；εi为误差项。

对式(5)微分可得

dy=c1dx1+…+2cn+1x1dx1+…+
c2n+1d(x1x2)+…+εi

(6)

当式(6)中交互项为零或值很小时，可得到各参数的主效应。线性项的主效应为

Mxi=cidxi

(7)

二阶项的主效应为

(8)

当交互项不可忽略时，则参数间的交互效应如式(9)所示

Mxixj=cmd(xixj)

(9)

3.2 参数贡献率计算原理

为了计算各个参数的贡献率，需建立样本点和评价指标之间的近似模型。首先通过式(10)将各主定参数值归一化至[-1,+1]，以消除21个主定参数自身数值大小的影响。

(10)

主定参数的贡献率采用响应面模型方法来计算，模型可分为多元一次回归模型、多元二次回归模型等，表达式分别为

(11)

(12)

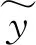
(13)

3.3 评价指标选取

如图4所示，不同参数条件下，弹体侵彻深度、弹体磨蚀程度及靶体损伤程度均不同。因此，分别选择侵彻深度H、弹体质量损失率及靶体损伤度D作为评价指标，进行参数敏感性分析。

图4 不同工况下的仿真结果

其中，侵彻深度根据计算结果直接获得。弹体的质量损失率通过提取弹体单元体质量变化曲线计算得到。而对于靶体损伤度的表征，则是通过将侵彻过程中已经删除的单元损伤度定义为1，并提取剩余所有单元的损伤度进行累加获得。典型靶体的全模型损伤分布如图5所示。

图5 工况41全模型的损伤情况

4 RHT模型参数敏感性结果

数值模拟获得的有效工况共计355个。剩余45个工况则因为参数取值不合理，导致计算时靶体单元体中出现复杂声速，或由于靶体强度过低，弹体将贯穿靶体而不采用。提取各工况的侵彻深度、弹体质量损失率及靶体损伤度作为敏感性分析的评价指标进行后续分析。

4.1 参数交互效应分析

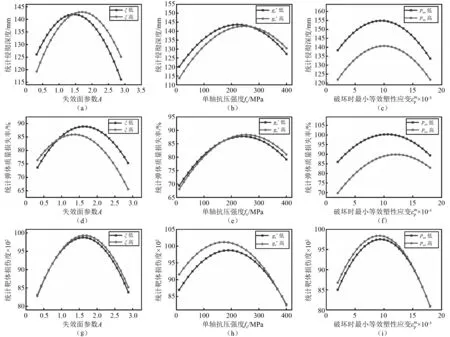
图6 对于不同评价指标的部分参数间的交互效应图

因此，对于同一评价指标，不同参数之间的交互效应不同。同时，对于不同评价指标，某两个参数之间的交互效应也可能存在差异。为了进一步描述参数之间的交互效应，取21个主定参数进行总体参数间交互效应分析。

SPSS(statistical product and service solutions)软件是一个功能强大的统计分析软件，通过SPSS软件可以对参数交互效应进行计算，并获得相应的显著性结果(significance，Sig)，当Sig值小于0.05时，说明此时参数交互效应显著，参数间将互相影响，反之则不显著。结果表明：当评价指标为侵彻深度时，21个主定参数组合的交叉效应Sig值为0.296>0.05；当评价指标为弹体质量损失率时，交叉效应Sig值为0.397>0.05；当评价指标为靶体损伤度时，交叉效应Sig值为0.995>0.05。因此，对于侵彻深度、弹体质量损失率与靶体损伤度而言，总体主定参数组合间的交互效应均不显著。

4.2 参数主效应分析

为了研究参数变化对评价指标的影响规律，针对各评价指标进行参数主效应分析，结果如图7～图9所示。其中，横坐标表示参数取值从低水平(对应1)依次变化至高水平(对应2)，纵坐标表示计算得到的评价指标的统计值。对于侵彻深度与靶体损伤度，各主定参数的主效应均呈非线性及非单调性变化。当各主定参数从低水平值变化至高水平值时，侵彻深度及靶体损伤度均将先增大后减小。对于弹体质量损失率，除了材料参数s外，其余参数对指标的主效应亦呈非线性及非单调性变化。而当s值增加时，弹体的质量统计损失率将降低。

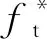
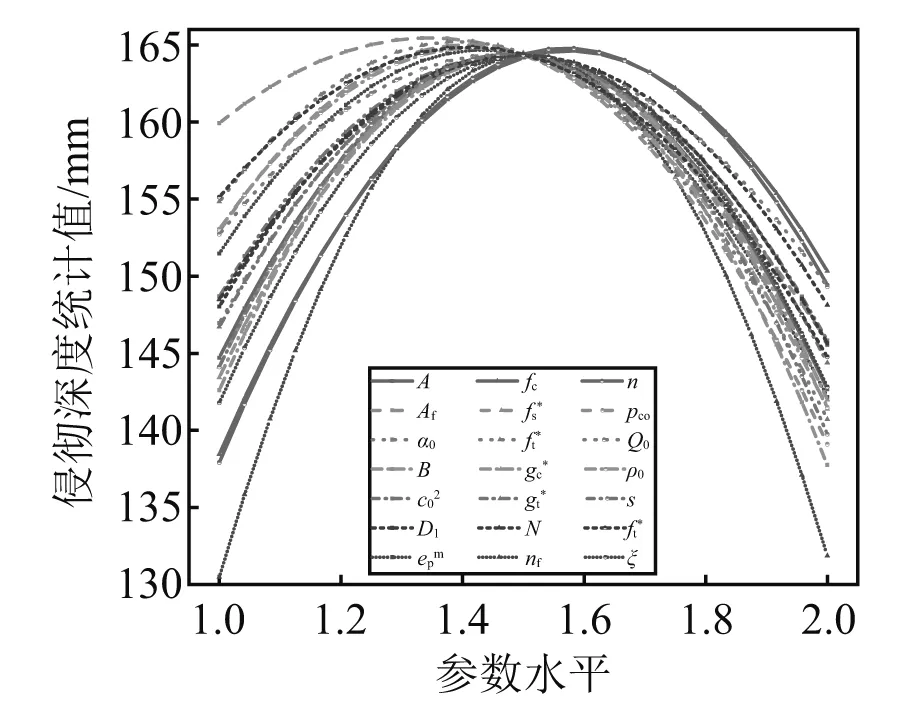
图7 侵彻深度主效应图

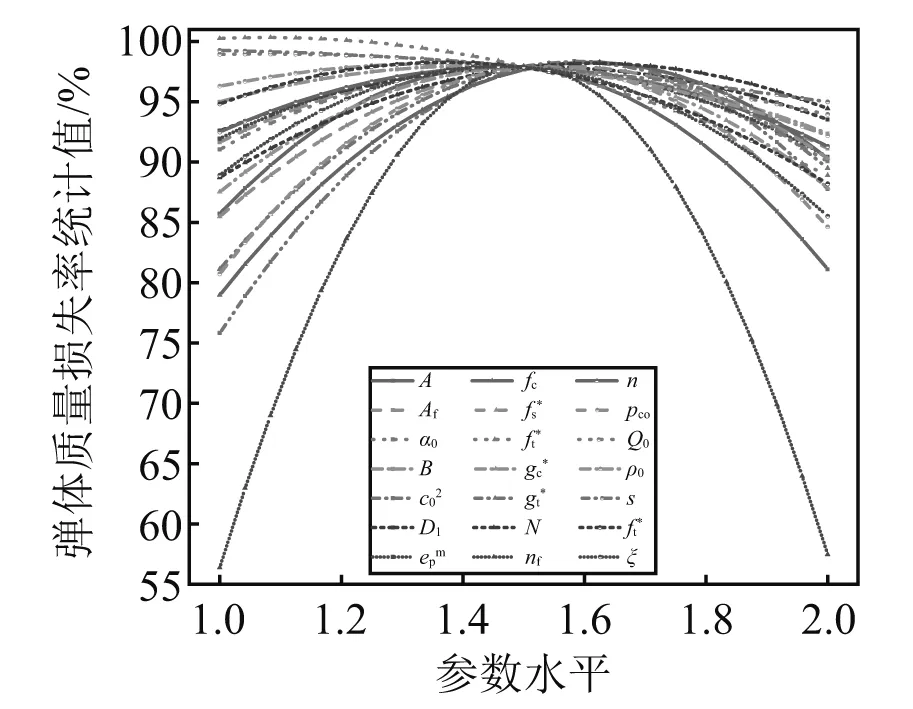
图8 弹体质量损失率主效应图

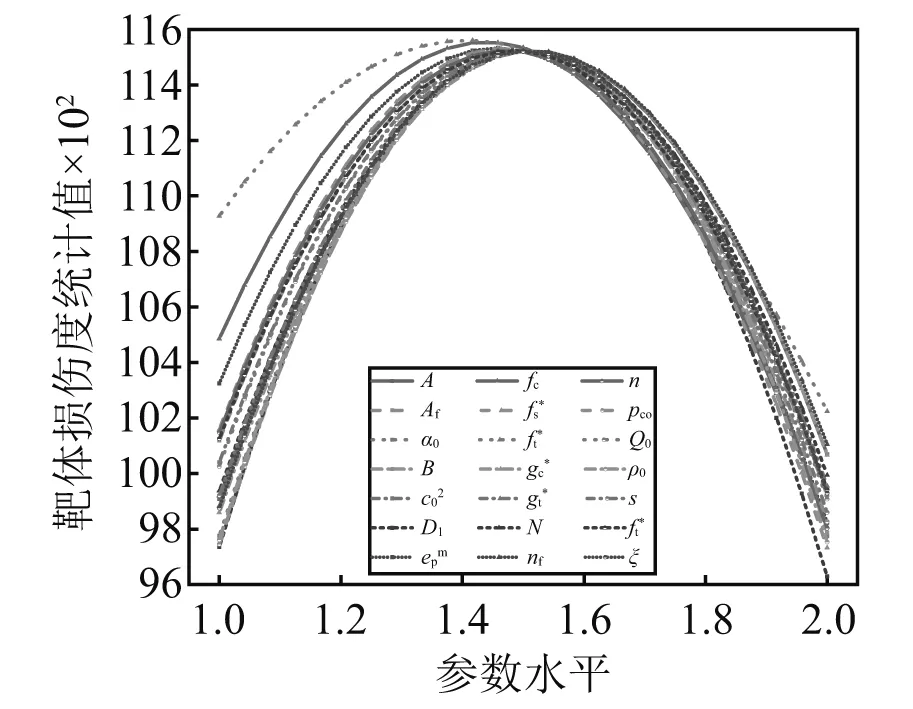
图9 靶体损伤度主效应图

4.3 近似模型及参数贡献率分析

分别建立一阶、二阶、三阶响应面模型，并利用355个侵彻深度、弹体质量损失率及靶体损伤度结果进行误差分析，结果如图10所示。其中，平行于横坐标的水平线表示用于计算的所有样本点的评价指标的实际平均值，对角线表示实际值与模型预测值相等的情况，点越靠近对角线则表明模型预测越精确。同时，为了定量评价各响应面模型对所有实际评价指标值的回归拟合效果，计算各模型的可决系数R2(coefficient of determination)如表5所示，当R2越接近1，则回归拟合效果越好。由图10可知，对于侵彻深度、弹体质量损失率及靶体损伤度，均为一阶响应面模型误差显著大于二阶与三阶响应面模型，即主定参数与评价指标间的函数关系具有较强的非线性。同时，由于二阶模型与三阶模型的可决系数差异较小，考虑到三阶响应面模型较二阶模型更为复杂，故选择二阶响应面模型进行后续参数贡献率计算。

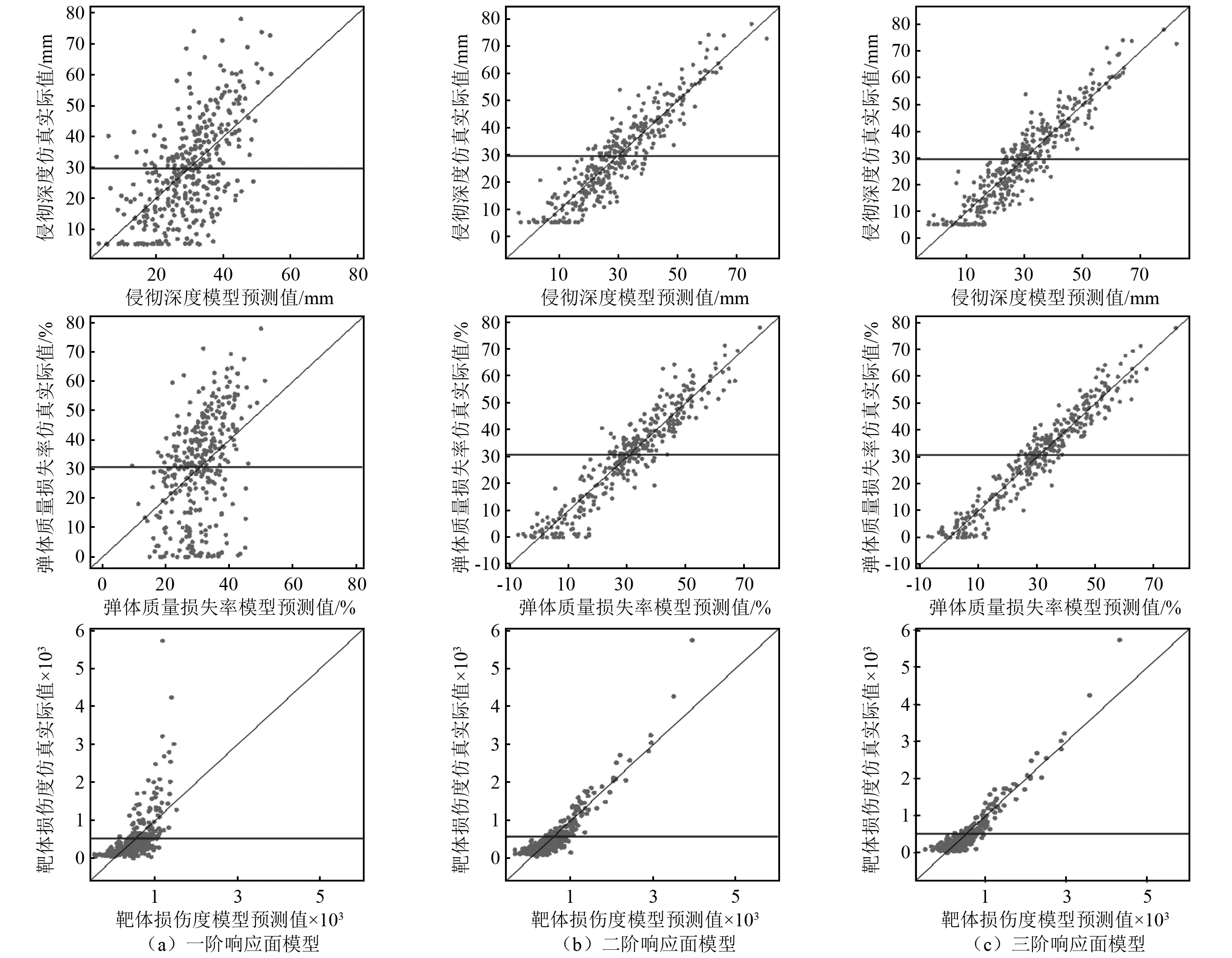
图10 各阶响应面模型误差分析图

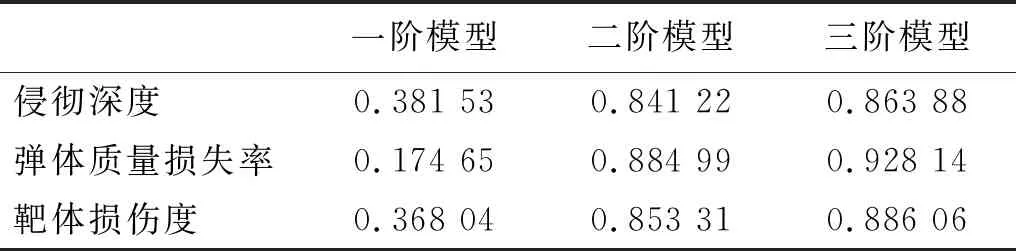
表5 各阶响应面模型可决系数R2结果

基于二阶响应面模型，分别对侵彻深度、弹体质量损失率及靶体损伤度计算各参数项的贡献率，并提取绝对值较大的前21项，如图11所示。结果表明，对于侵彻深度及靶体损伤度而言，参数二次项对评价指标的影响普遍较一次项及交互项大。对于弹体质量损失率而言，贡献率较大的参数项同样以二次项居多。

为了较全面地衡量各主定参数的贡献率情况，按下式计算各个主定参数总体贡献率

(14)

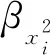
表6 各主定参数总体贡献率

5 结 论

本文针对弹体侵彻半无限厚岩石靶体问题，利用优化拉丁超立方设计算法设计了参数试验矩阵，并进行数值模拟。根据355个有效结果，以侵彻深度、弹体质量损失率及靶体损伤度为评价指标，对21个主定参数进行了参数敏感性分析，并得到了以下结论：

(1) 主定参数间存在一定交互效应，且不同参数之间的交互效应不同。同时，对于不同评价指标，参数间的交互效应亦存在差异。取21个主定参数对侵彻深度、弹体质量损失率及靶体损伤度进行总体参数组合间交互效应分析，其结果均为交互效应不显著。

(2) 对于侵彻深度与靶体损伤度，各主定参数的主效应曲线均呈非线性及非单调性变化。随着参数水平值增加，侵彻深度及靶体损伤度的统计值均将先增大后减小。而对于弹体质量损失率，材料参数s的值增加时，弹体质量统计损失率将降低。其余参数的主效应则与侵彻深度和靶体损伤度相似。

(3) 对于不同评价指标，各参数的主效应不一致。对于侵彻深度及弹体质量损失率而言，残余应力强度指数的主效应最显著。此外，当参数水平变化时，各主定参数间的主效应相对显著情况将发生变化。