改进变分模态分解包络谱分析在自动扶梯轴承故障诊断中的应用
2021-07-22张毅郝高岩刘璇
张毅,郝高岩,刘璇
(1.北京市轨道交通建设管理有限公司,北京 100068;2.城市轨道交通全自动运行系统与安全监控北京市重点实验室, 北京 100068;3.北京博华信智科技股份有限公司,北京 100029;4.洛阳轴承研究所有限公司,河南 洛阳 471039)
自动扶梯电动机、齿轮箱、驱动轴等关键部件的轴承故障时有发生,属于典型的旋转机械类故障,通常在关键部位安装振动传感器获取振动数据并通过带通滤波和包络解调等方法识别故障[1-2]。对于轴承等关键部件的早期故障,故障冲击特征易被淹没在其他高幅值的设备运转噪声中,且由于信号的随机性和非平稳性,常规的带通滤波和包络解调方法仅为近似平均方法,无法真实刻画实际信号特征。
目前,信号的自适应分解技术由于摆脱了傅里叶分析、小波分析[3]等固定基函数的缺陷,可针对原始非平稳信号自适应选择分解模式,经验模态分解(EMD)[4-5]方法的分解效果高度依赖极值点的查找、极值点的拟合方法以及迭代的结束条件,且缺乏一定的数学理论基础,这些条件决定了EMD方法的鲁棒性不佳。
变分模态分解(Variational Mode Decomposition,VMD)方法克服了EMD方法的不足[7],在轴承故障诊断中应用广泛:文献[8-12]利用包络熵对变分模态分解参数进行优化,但包络熵计算复杂,且没有考虑信号相关性;文献[13]对分解层数和惩罚因子的影响关系进行分析,利用分量信号的能量之和占原信号能量的比值判断分解效果,从而找出变分模态分解的最佳分解层数,但其无法准确确认惩罚因子;文献[14]仅利用峭度指标作为寻优适应度函数,导致出现了过分解问题。综上分析,本文提出新的适应度函数寻优算法对变分模态分解的分解层数和惩罚因子进行寻优,并通过自动扶梯电机轴承的真实故障数据进行验证分析。
1 变分模态分解及工作原理
变分模态分解可理解为将原信号分解为具有一定中心频率和带宽的子信号,其主要步骤为[9]:
1)对每一个模态分量uk,求得实信号的解析信号。
2)将uk与具有中心频率ωk的复指数信号相乘,把各模态分量的频率搬移到基带。
3)通过调制信号的高斯平滑度方法估计各模态分量的带宽,即梯度的L2范数。
以上过程转换为约束变分问题,即
(1)
式中:uk为分解得到的第k个模态分量;ωk为第k个模态分量的中心频率;δ(t)为脉冲函数;f为原信号。

(2)
(3)
(4)
式中:α为带宽惩罚因子;τ为双上升步长;λ为拉格朗日乘子;ε为误差因子,f(ω)为信号频域。
重复(2)—(4)式进行更新,满足迭代停止条件时结束循环[7],得到K个IMF分量。
2 基于改进变分模态分解的包络谱分析
2.1 蜻蜓优化算法
蜻蜓优化算法(Dragonfly Algorithm,DA)是一种新型智能优化算法[15],该算法模拟蜻蜓的生活习性并将其归纳为5类行为方式:分离、对齐、内聚、寻找食物和远离天敌。
根据蜻蜓行为方式进行蜻蜓位置的更新迭代[16],计算公式为
Xt+1=Xt+ΔXt+1,
(5)
ΔXt+1=(sSi+aAi+cCi+fFi+eEi)+wΔXt,
式中:ΔXt+1为位置更新步长;t为当前迭代次数;s为分离度权重;Si为第i个个体的分离度;a为对齐度权重;Ai为第i个个体的对齐度;c为内聚度权重;Ci为第i个个体的内聚度;f为食物因子;Fi为食物位置对第i个个体的吸引力;e为天敌因子;Ei为天敌位置对第i个个体的排斥力;w为惯性权重。
引入Lévy飞行随机游走方法进行蜻蜓位置更新,即
Xt+1=Xt+Lévy(d)ΔXt,
(6)

(7)
Γ(x)=(x-1)!,
式中:d为维度;r1,r2为[0,1]范围内的随机数;β为常数,此处取值为1.5。
2.2 基于DA优化的变分模态分解
变分模态分解的实际使用中,需要人为确定分解层数K和惩罚因子α,因此,本文结合蜻蜓优化方法构造新的适应度函数,提出自适应的变分模态分解方法,主要步骤为:
1)对蜻蜓优化算法参数进行初始化,初始化群体个数为20,迭代次数为10;蜻蜓位置初始化,初始化K∈[2,10],α∈[500,10 000],两者在该范围内随机取值;初始化位置变化步长。
2)计算各权重值,根据初始值随机初始化初始参数s,f,w,a,c,e。
3)采用相关系数与峭度的乘积构造适应度函数,即
Ti=max(ciki);s.t.ki>3.2,
(8)
式中:ci为第i个分量的相关系数;ki为第i个分量的峭度,为避免相关性很大而信噪比较小的情况,仅考虑峭度大于3.2的分量。
4)依据(6)式更新蜻蜓位置,迭代蜻蜓位置及步长,满足最大迭代次数后停止程序。
5)采用最优的K和α进行变分模态分解,对分解后适应度最大的分量进行希尔伯特包络分析并计算包络波形的频谱,观察包络谱中是否存在明显的轴承故障特征频率。
3 轴承故障数据验证
采用凯斯西储大学轴承故障数据进行算法验证,使用1 750 r/min转速工况下驱动端6205-2RS深沟球轴承的数据,其外圈故障特征频率为104.7 Hz,内圈故障特征频率为157.5 Hz。为验证算法在实际工况下的有效性,分别在外圈、内圈原始信号中加入-15,-10 dB的白噪声信号。
3.1 外圈故障
轴承外圈故障振动信号的时域波形及其包络谱如图1所示,故障特征频率被淹没在噪声中,包络谱中也无法有效提取轴承故障特征频率。

图1 轴承外圈故障振动信号的时域波形及其包络谱Fig.1 Time domain waveform and envelope spectrum of bearing outer ring fault vibration signal
对轴承外圈故障振动信号进行变分模态分解,采用新构造的适应度函数进行蜻蜓寻优,确定分解参数K=6,α=5 200,分解所得IMF分量如图2所示,各分量的相关系数、峭度及其乘积见表1。分析可知IMF4分量的适应度值最大,且其时域波形中有一些冲击成分,因此选择IMF4分量进行包络解调,从图3所示包络谱中可明显观察到轴承外圈故障特征频率及其2倍频。

图2 轴承外圈故障振动信号变分模态分解所得分量(K=6,α=5 200)Fig.2 VMD components of bearing outer ring fault vibration signal(K=6,α=5 200)
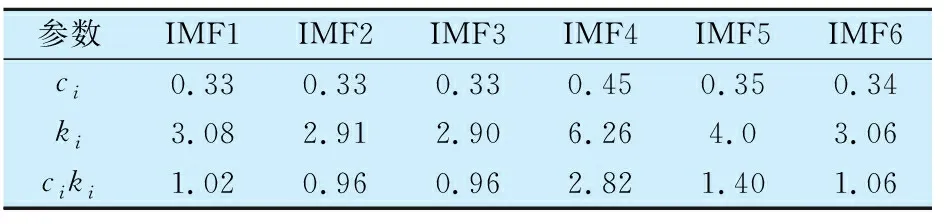
表1 轴承外圈故障振动信号各IMF分量的相关系数及峭度(K=6,α=5 200)Tab.1 Correlation coefficient and kurtosis of IMF of bearing outer ring fault vibration signal(K=6,α=5 200)

图3 轴承外圈故障振动信号IMF4分量的包络谱(K=6,α=5 200)Fig.3 IMF4 envelope spectrum of bearing outer ring fault vibration signal(K=6,α=5 200)
3.2 内圈故障
轴承内圈故障振动信号的时域波形及其包络谱如图4所示,同样无法发现轴承内圈故障特征频率。采用新构造的适应度函数进行蜻蜓寻优可得K=4,α=8 820,变分模态分解所得IMF分量如图5所示,各分量的相关系数、峭度及其乘积见表2。分析可知IMF3分量的适应度值最大,其包络谱如图6所示,可明显观察到轴承内圈故障特征频率及其2倍频(315.7 Hz)、3倍频(473.1 Hz)。

图4 轴承内圈故障振动信号的时域波形及其包络谱Fig.4 Time domain waveform and envelope spectrum of bearing inner ring fault vibration signal

图5 轴承内圈故障振动信号变分模态分解所得分量(K=4,α=8 820)Fig.5 VMD components of bearing inner ring fault vibration signal(K=4,α=8 820)

表2 轴承内圈故障振动信号各IMF分量的相关系数及峭度(K=4,α=8 820)Tab.2 Correlation coefficient and kurtosis of IMF of bearing inner ring fault vibration signal(K=4,α=8 820)
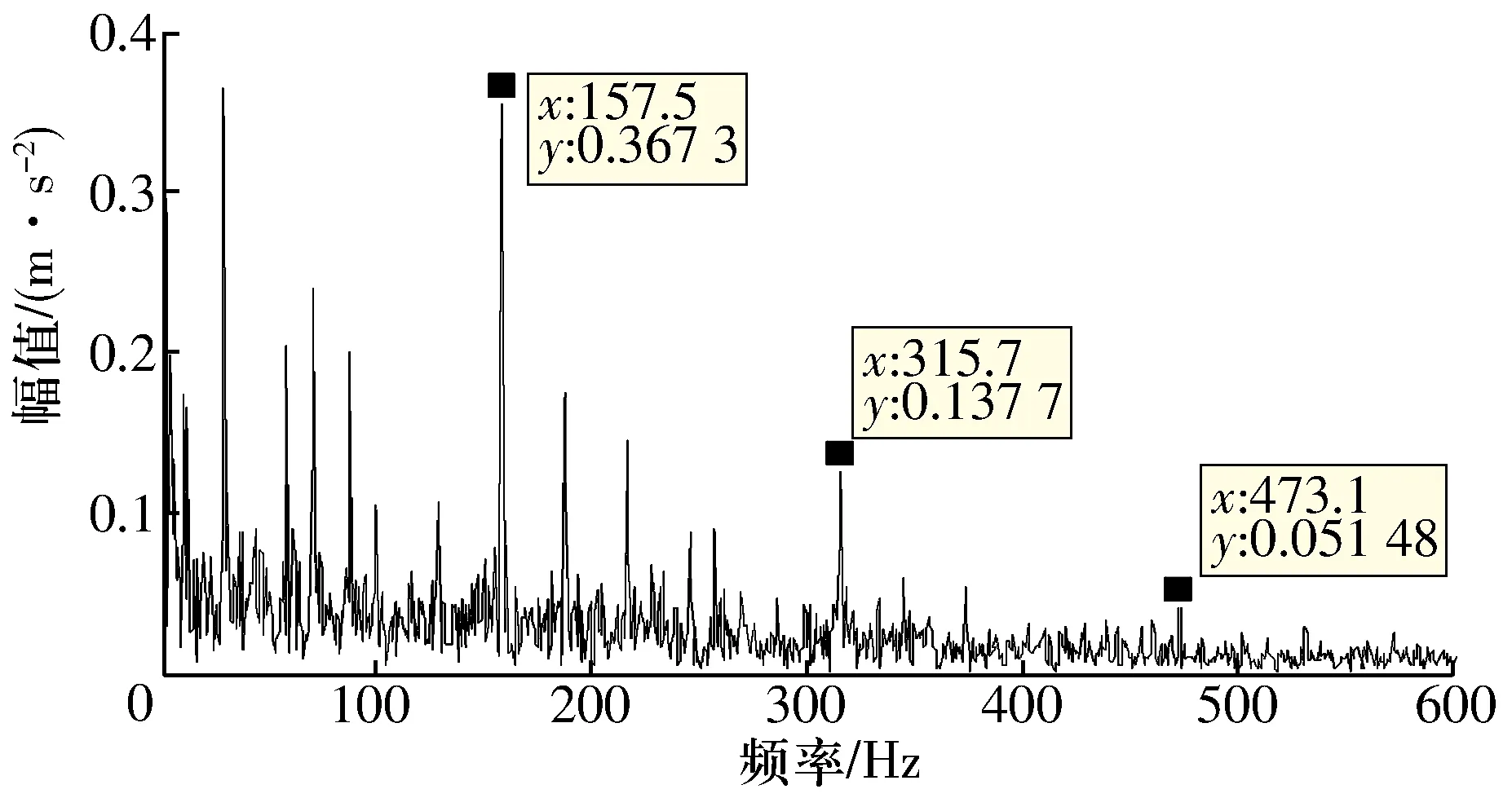
图6 轴承内圈故障振动信号IMF3分量的包络谱Fig.6 IMF3 envelope spectrum of bearing inner ring fault vibration signal
3.3 对比分析
为验证本文所提适应度函数的优越性,仅采用峭度作为适应度进行寻优,得到外圈故障(K=9,α=4 880)、内圈故障(K=9,α=5 500)的最佳参数并选择峭度最大的分量进行包络谱分析,结果如图7所示。由图7可知:可以观察到轴承外圈故障特征频率104.7 Hz但幅值相对较低,而其2倍频则被噪声淹没;轴承内圈故障特征频率157.5Hz相对明显,但同样观察不到其倍频特征;本文所提适应度函数兼顾了轴承故障冲击信号特征及与原信号的相关性,能更好的反映轴承的故障特征。
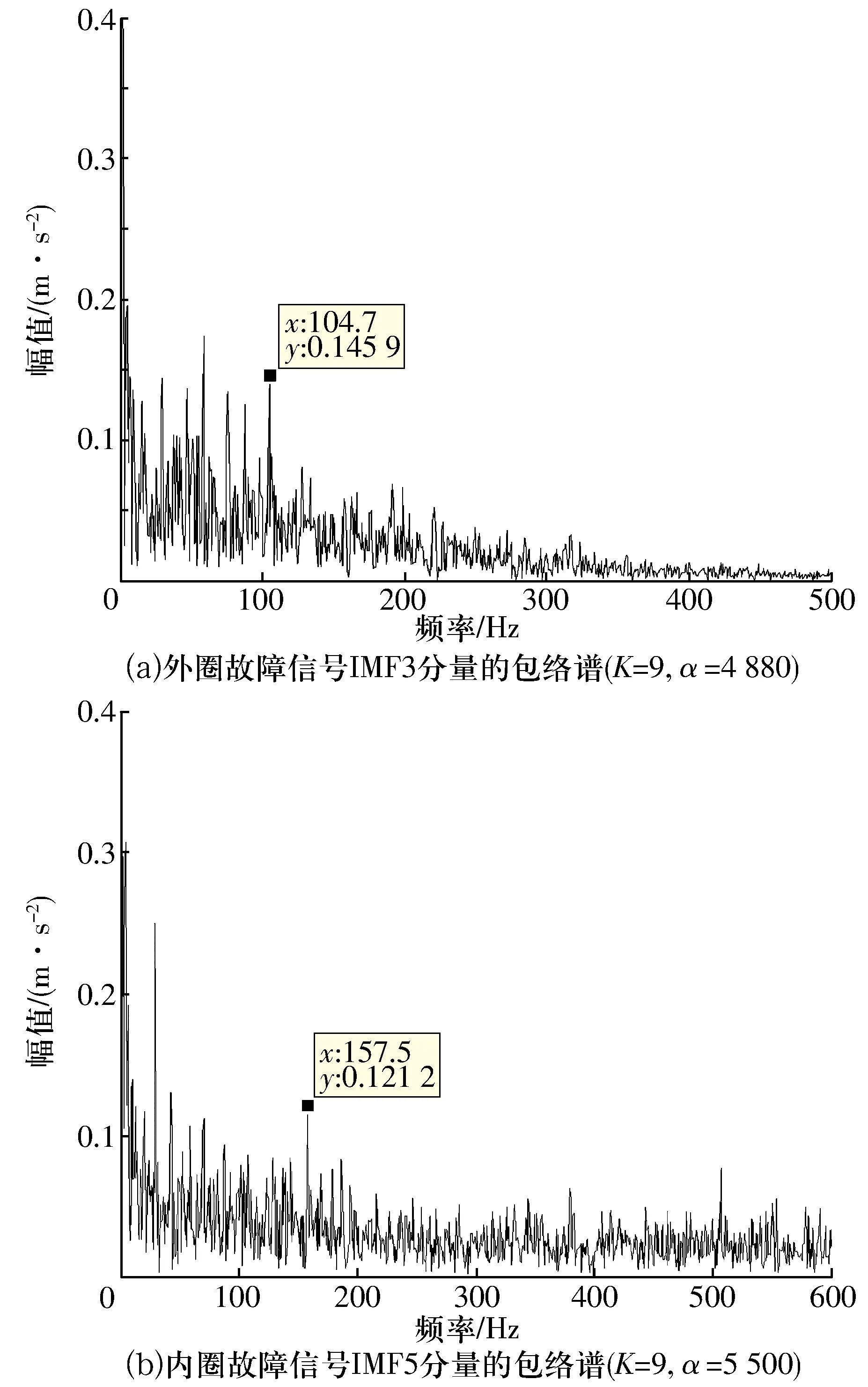
图7 峭度作为适应度函数时的故障特征提取结果Fig.7 Fault feature extraction results of kurtosis as fitness function
4 自动扶梯电机轴承故障诊断
对某自动扶梯电机轴承故障进行诊断分析,自动扶梯类型为单驱动,运行速度0.51 m/s,电动机实际转速778 r/min,转频12.97 Hz。轴承型号为6310,在运行转速下轴承外圈故障特征频率为39.516 Hz,内圈故障特征频率为64.217 Hz。
采集电机轴承机壳处的振动加速度,采样频率12 800 Hz,采样点数16 384,所采集振动信号的时域波形及其频谱、包络谱如图8所示,从图中无法有效判别轴承状态,故障特征频率淹没在噪声和变频器干扰(78 Hz为间隔的高频成分)中。

图8 自动扶梯电机轴承振动信号的时域波形及其频谱、包络谱Fig.8 Time domain waveform,spectrum and envelope spectrum of vibration signal of escalator motor bearing
采用改进的变分模态分解方法,以新构造的适应度函数进行蜻蜓寻优获得最优的分解参数为K=4,α=5 800。采用最优参数进行变分模态分解,所得分量如图9所示,各分量的相关系数、峭度及其乘积见表3。分析可知:IMF2分量的适应度值最大且其时域波形中具有明显的周期性轴承故障冲击特征。

图9 自动扶梯电机轴承振动信号变分模态分解所得分量Fig.9 VMD components of vibration signal of escalator motor bearing
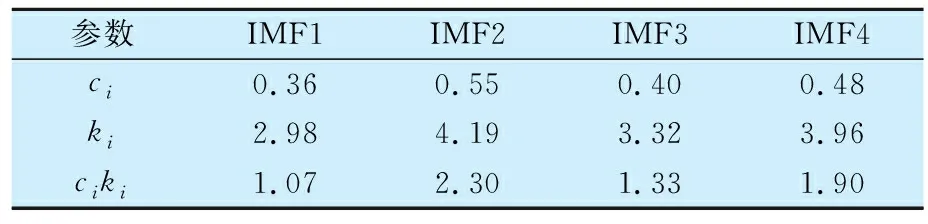
表3 自动扶梯电机轴承各IMF分量的相关系数及峭度Tab.3 Correlation coefficient and kurtosis of IMF of vibration signal of escalator motor bearing
对IMF2分量进行希尔伯特包络解调分析,结果如图10所示,从包络谱中可明显观察到40.63,80.47,121.1,160.9,201.6 Hz频率处存在明显谱峰,与自动扶梯电机轴承外圈故障特征频率及其倍频相近,因此判定自动扶梯电机轴承存在外圈故障,与拆机检查结果一致,说明本文方法有效可行。

图10 自动扶梯电机轴承IMF2分量的包络谱Fig.10 IMF2 envelope spectrum of vibration signal of escalator motor bearing
5 结束语
结合蜻蜓优化算法,以相关系数与峭度的乘积作为适应度函数,对变分模态分解的分解层数和惩罚因子进行寻优,新构造的适应度函数兼顾了峭度指标的冲击敏感性和IMF分量与原信号的相关性,避免了仅通过峭度为适应度函数易出现的过分解问题。
试验台数据以及自动扶梯电机轴承的分析结果表明,改进变分模态分解与包络谱分析相结合的方法能够在低信噪比情况下充分提取轴承故障特征信息,在轴承故障诊断中具有较好的应用前景。
