汽车动力总成悬置结构设计方法的研究
2021-07-22夏彰阳丁行武卜继玲贺新峰
夏彰阳,丁行武,卜继玲,贺新峰
(1.株洲时代新材料科技股份有限公司,湖南 株洲 412007;2.中车时代电动汽车股份有限公司,湖南 株洲 412007)
随着汽车行业竞争的加剧,汽车产品的开发需要兼顾成本与周期,各种高效、低成本的设计方法已成为重要的研发手段[1-4]。仿真技术作为常用的设计方法,能有效缩短产品设计周期、提高产品性能和减少昂贵样件试制次数[5-8]。
汽车动力总成悬置(简称悬置)作为连接发动机与车架的弹性部件,其性能直接影响汽车的操纵稳定性和平顺性[9-11]。悬置各向刚度是影响悬置性能的主要因素之一,为了使悬置各向刚度符合设计要求,需要对悬置中的橡胶区域进行优化设计,这是悬置设计的重点和难点[12-13]。目前国外厂家采用多次迭代优化实现产品结构设计,而国内厂家主要通过产品性能试验不断修改悬置结构以满足设计要求。因此,提升设计能力已成为悬置结构研究的重点工作。
本工作以某汽车悬置为研究对象,采用仿真技术对其结构进行优化设计,得到三向刚度符合要求且应力较低的悬置结构。
1 悬置结构设计要求
本工作前期完成了悬置固有频率和解耦率的匹配优化[14-18],提取悬置三向(弹性主轴x,y和z向)线性刚度,其x,y和z向线性刚度分别为125,213和65 N·mm-1。
为满足车架和动力总成支架的设计空间,悬置结构如图1所示,其中悬置外套与动力总成支架固定连接,悬置芯子与车架固定连接,两者通过橡胶主簧实现连接,可有效隔离由动力总成激励引起的车架或车身的振动和噪声。橡胶主簧采用Yeoh模型的橡胶材料,其材料参数C10,C20和D1分别为0.60,0.03和3.30×10-4。

图1 悬置结构示意Fig.1 Diagram of mount structure
2 悬置结构设计
根据悬置结构技术要求,对其进行包括拓扑优化、参数优化、形状优化及限位设计的设计方法研究,具体设计流程如图2所示。

图2 悬置结构设计优化流程Fig.2 Optimization process of mount structure design
2.1 拓扑优化
在产品设计前期,运用拓扑优化方法可以得到合理的悬置材料布局,为悬置结构设计提供概念方案。
2.1.1 数学模型
连续体拓扑优化的方法主要有变密度、变厚度和均匀化方法。本工作采用变密度方法展开拓扑优化设计,其基本思路是引入一种相对密度为0~1的材料,将连续结构体离散为有限元模型后,以每个单元的密度为设计变量。这样,悬置结构的拓扑优化问题转化为单元材料的最优分布问题。
以材料体积为目标函数,悬置各向线性刚度为约束条件,设计空间内各单元相对密度为设计变量,则悬置结构拓扑优化的数学模型为:
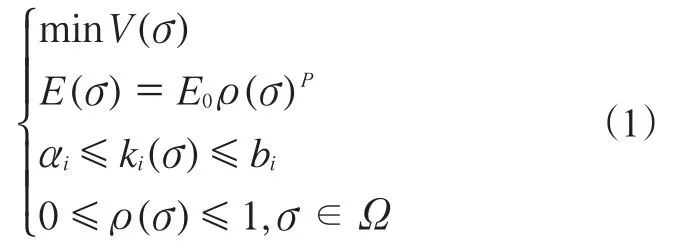
式中:V(σ)为目标函数,σ为与设计有关的变量;E(σ)为材料弹性模量与材料密度相关的函数,E0为材料弹性模量;ρ(σ)为与材料密度相关的函数,P为惩罚因子;ki(σ)为某方向线性刚度,αi为线性刚度下限,bi为线性刚度上限,i=x,y,z(3个弹性主轴方向);Ω为材料区的体积。
2.1.2 初始模型
在进行悬置结构拓扑优化过程中,必须先确定拓扑对象的设计空间和非设计空间。设计空间为需要拓扑优化的区域,非设计空间为拓扑优化过程中的固定区域。由于悬置芯子和外套为装配部件,因此定义其为非设计空间,橡胶主簧定义为设计空间[19-20]。
悬置结构拓扑优化初始模型如图3所示。图中,黄色区域为悬置外套与支架配合位置,对其施加固定约束;蓝色区域为悬置芯子内孔表面,通过参考点与其耦合约束,对参考点施加位移载荷,提取参考点的反作用力,即可得到线性刚度。
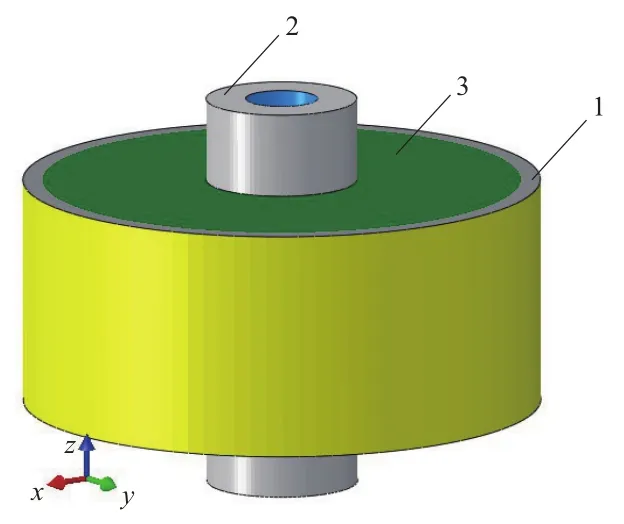
图3 悬置结构拓扑优化初始模型Fig.3 Initial model of mount structure topology optimization
2.1.3 优化结果
基于式(1)的数学模型,将悬置线性刚度约束波动范围调整为±20%。考虑工艺因素,添加了拔模约束和对称约束,拔模方向和对称平面均参考图3所示的坐标系,原点为模型中心点。同时,为得到比较均匀的材料分布,添加了最小尺寸约束。基于TOSCA Structure软件对悬置结构初始模型进行拓扑优化,其数学模型如式(2),优化结果如式图4所示。
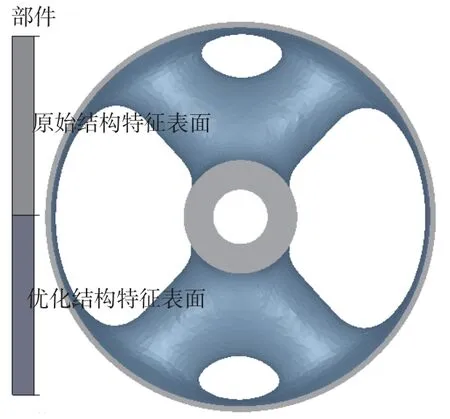
图4 悬置结构初始模型优化结果Fig.4 Optimization result of mount structure initial model
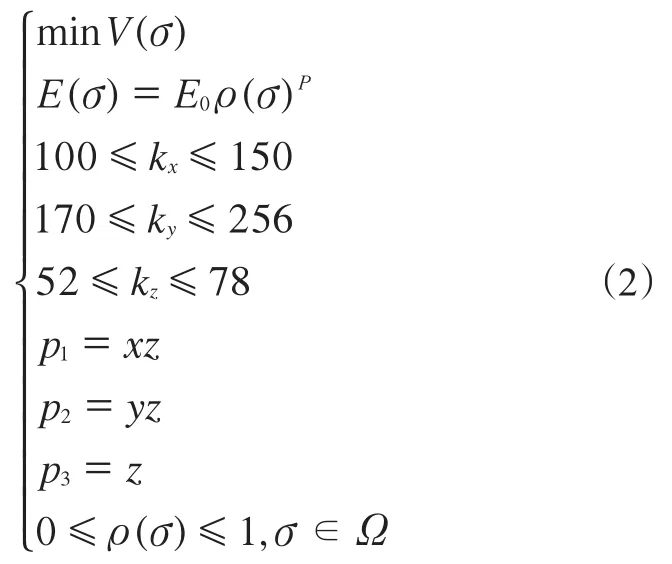
式中:p1为平面对称约束1,沿xz平面中心对称;p2为平面对称约束2,沿yz平面中心对称;p3为拔模方向,沿z向。
由于悬置y向线性刚度大于x向线性刚度,导致优化结果中悬置在x向的材料分布小于y向的材料分布。同时悬置概念结构方便添加限位,可作为原始设计方案。
2.2 参数优化
确定悬置概念结构后,进一步参数化悬置结构的关键尺寸,通过优化参数值来实现悬置各向线性刚度的匹配。
2.2.1 参数化模型
根据悬置结构特点,选取橡胶主簧关键尺寸[包括橡胶层轴向高度(H)、宽度(L)和角度(θ),如图5所示]进行参数化处理。
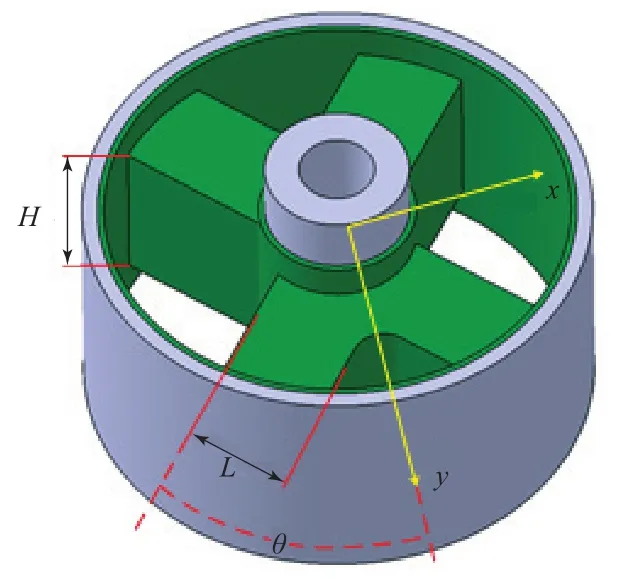
图5 悬置结构参数化尺寸示意Fig.5 Parametric dimensions of mount structure
以悬置三向线性刚度最小为目标函数,H,L和θ为设计变量,根据悬置实际尺寸约束设计变量取值范围,得到优化数学模型为:

在Abaqus软件中建立参数化模型,并计算悬置三向线性刚度,集成Isight优化平台[21]。按照式(3)定义优化目标和约束范围,采用多岛遗传算法对悬置结构进行参数优化,具体流程见图6。

图6 悬置结构参数优化流程Fig.6 Optimization process of mount structure parameters
2.2.2 优化结果
通过迭代寻优计算,优化后橡胶主簧H,L和θ尺寸分别为27.3 mm,17.3 mm和39.9°,悬置三向线性刚度优化结果如表1所示,优化后悬置x,y和z向刚度偏差分别为2.00%,0.05%,2.46%,均小于3%,满足技术要求。

表1 悬置三向线性刚度优化结果Tab.1 Optimization results of mount three dimensional linear stiffness N·mm-1
2.3 形状优化
通过上述优化设计,初步确定了悬置结构的尺寸,为了延长悬置的使用寿命,需通过形状优化降低其最大主应力。
2.3.1 形状优化模型
根据参数优化结果,计算悬置在各个方向的应力水平,确定其最大主应力位置,如图7所示。
由图7可知,悬置的标记区域内存在一定程度的应力集中,形状优化时将标记区域定义为优化区域。基于以上有限元分析结果,通过TOSCA Structure软件形状优化模块自动修改优化区域表面几何节点位移,以悬置三向最大主应力最小为目标,进行形状优化,数学模型如式(4)所示。
在施工之前,施工单位需要对施工周围建筑的桩基结构进行充分的了解,掌握地下管线的分布情况,同时做好自然条件的勘察工作,保证计划的合理性。如若在施工过程中发现问题,要及时记录并分析,积极寻找解决问题的方法。施工时要对开挖工作进行实时检测,保证每一步工作的安全合理,同时可以对安全问题进行规避。如若在开挖过程中出现严重的变形,则需要先对深基坑进行加固处理,防止水土对施工造成不必要的影响。基坑围护结构分为3种:加固型、支挡型和混合型。土钉墙属于加固型,经济适用,因而在基坑维护中应用广泛。

图7 悬置三向应力云图Fig.7 Nephograms of mount three dimensional stresses

式中,sx为x向加载最大主应力,sy为y向加载最大主应力,sz为z向加载最大主应力,nd为优化区域表面几何节点位移,V0为悬置优化前体积,V为悬置优化后体积。
2.3.2 优化结果
悬置三向最大主应力迭代曲线如图8所示。
从图8可以看出:y和z向加载时,悬置最大主应力有明显的降低;x向加载时,悬置最大主应力基本不变。基于形状优化的计算结果,进一步改进悬置应力集中区域的结构特征。

图8 悬置三向最大主应力迭代曲线Fig.8 Iteration curves of mount three dimensional maximum principal stresses
2.4 限位设计
经过拓扑优化、参数优化以及形状优化,悬置在满足刚度设计要求的同时,其最大主应力也得到降低。然而在实际使用过程中,为了避免悬置的过度变形,需要进行限位设计,使悬置在变形过程中的刚度曲线呈非线性。根据通用汽车公司GMW14116标准要求[22],悬置力-位移关系曲线(非线性曲线设计准则)如图9所示(AFM为主动燃料管理,WOT为节气门全开)。
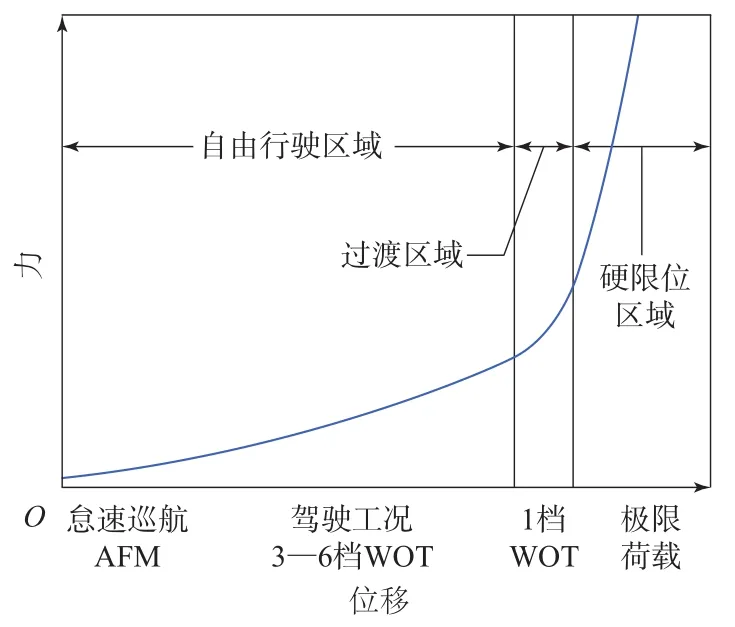
图9 悬置力-位移关系曲线Fig.9 Curve of mount force-displacement relation
由图9可知,极限工况时,悬置承受极限荷载,此时限位区域起控制动力总成运动范围的作用。通过计算得到悬置系统在典型工况下的力-位移关系[23],从而可确定悬置各向非线性曲线以及限位起始位置,结合优化得到的悬置结构,完成最终悬置结构设计,如图10所示。

图10 最终悬置结构Fig.10 Final structure of mount
3 结论
(2)基于设计要求进行悬置结构设计研究。拓扑优化后,悬置概念结构作为原始设计方案;参数优化后,悬置各向线性刚度偏差均小于3%,满足技术要求;形状优化后,悬置y和z向最大主应力有明显的降低;限位设计后,得到最终悬置结构。
(3)本工作的设计方法和设计思路不仅适用于悬置类产品设计,也可为汽车上其他部件的设计提供参考。
