基于“三新企业”抽样调查的事后分层复合抽样设计

张维群,段格格

(西安财经大学 统计学院,陕西 西安 710100)

一、引言

随着新一代信息技术的兴起,催生了一批具有成长速度快、创新能力强、发展潜力大等特点的“三新企业”,“三新”是经济发展新业态、新产业、新商业模式的统称。2018年,“三新”经济一词正式列入国家统计局统计名词库,并单独成立专项调查。以往是通过五年一次的经济普查构建企业抽样框,但“三新企业”总体在短期内单位新生、消亡较为频繁,总体单位变化大,由于经济普查时间间隔相对较长,导致抽样框更新不及时,抽样框出现老化的情况,通过该抽样框获得的“三新企业”抽样样本必然对于总体的代表性下降。数据显示,2017年大型工业企业单位为9 240家,中型工业企业单位数为49 614家,小型工业企业单位数为313 875家,而2018年大型工业企业单位数为9 103家,中型工业企业单位数为49 778家,小型工业企业单位数为319 559家。若对2018年各类工业企业经营情况进行抽样调查,采用2017年的抽样框进行抽样设计,可能会导致各类企业中部分样本丢失或部分新生样本不包括在抽样框内,抽样样本对2018年工业企业总体的代表性较差,对于总体推断误差必然增大。在实践中,“三新企业”具有单位变动频繁以及目标变量水平变化大的特点,使用固定抽样框进行抽样时,可能抽取到部分企业当期已经消亡,而部分新生企业却未能被抽取到。在分层抽样中,存活企业的经营情况变化比较大,企业的分层归属也可能会发生变化,采用固定样本框进行抽样设计获得的样本对总体代表性难以保证,从而不能够对总体特征进行准确推断。因此,需要设计出符合动态总体特点的分层抽样方法,通过事后分层和各层总体容量的估计,构造事后分层复合统计量,实现对“三新企业”总体特征的准确推断,为“三新企业”统计调查提供理论参考。

目前,统计部门主要以定期普查为“三新企业”名录库提供信息,而“三新企业”规模小、数量多、变化快,给统计长期监测带来困难。“三新”经济催生出大量小微企业,且多属于规模以下企业,现行统计报表制度难以全面、及时反映“三新企业”的发展全貌,需要多种调查方法与手段相互配合,并对抽样技术进行创新。针对单一抽样框存在的问题,许多学者研究了两个或两个以上的单一抽样框相结合的方法进行抽样推断。Hartley认为当任何一个调查总体及其对应的抽样框都难以覆盖目标总体时,考虑使用两个不完整的子总体组合之后可以完全覆盖目标总体,然后通过构建相应的抽样框再进行随机抽样,并基于传统的估计方法提出了H估计量[1];由于H估计量存在着推断误差较大的问题,Lund对H估计量进行了改进,提出了方差更小的L估计量[2];同时,双重抽样框也存在着重叠区域的总体规模信息重复的问题,Fuller和Burmeister在H估计量基础上提出了有效性更好的F-B估计量,并且在简单随机抽样设计下提出了修正的F-B估计量[3];Bankier等人将双重抽样框组合看成一个单一抽样框,其思路是将双重抽样框不同区域信息赋予不同权重以实现总体的有效推断,通过调整不同区域的权重系数来实现对总体信息的推断,提出了SF估计量[4-6]。金勇进等较早地将多重抽样方法引入了国内抽样实践中,着重介绍了两个子总体及其双重抽样框方法[7-8];随后国内多重抽样理论研究也得到一定的发展,贺建风利用简单估计方法将现有多重抽样框理论进行统一,提出了HT估计量,并针对多指标分层抽样、二阶段抽样及连续性抽样等抽样实践中常用的特定抽样调查的多重抽样框估计方法进行研究,并应用于“三农”问题的调查研究中[9];由于抽样实践中抽样框变动对样本的代表性产生较大的影响,刘宾等针对中国中小企业抽样调查中由于抽样框变动导致企业代表性不足的问题,结合京津冀地区的实际情况,采用目录企业抽样与地域抽样相结合的抽样调查方式,此方法在方案设计上互补性较强,尤其是在新增企业的抽样调查上,可以减少新增企业与原有企业的实际分布不完全一致的问题,减少数据推断的误差[10]。

从文献研究看出,基于Hartley研究思路的基础上所构建的双重或多重抽样框,主要是用于解决传统抽样框无法完全覆盖总体信息的问题,进而使用不同的统计方法构造出精度更高的统计量,来实现对某个抽样框总体信息的补充。然而,动态总体由于其总体容量和单位特征在短期内会发生变化,不仅需要考虑对抽样框总体信息的补充,还需要删除已经消亡的样本信息以及更新各层样本信息,因此设计一种基于总体容量、总体单元和单位特征同时发生变化的抽样方法显得尤为重要。本文拟设计基于动态总体的事后分层复合抽样方法来估计总体的信息,估计各层总体消亡率和新生率,实现抽样框内动态总体规模和层划分的更新,以达到总体特征的准确推断。

二、动态总体的事后分层与复合抽样的设计

由于“三新”企业总体抽样框在短期内单位新生、消亡较为频繁,且总体中单位目标变量水平变化较大,而固定抽样框被认为总体在较长一段时间内是稳定不变的,采用固定抽样框设计“三新企业”抽样调查必然存在着问题。基于总体动态变化构造的抽样框不同于传统的固定抽样框,第一,此抽样框体现为前后两期抽样框总体单位不完全相同,可能出现前后两期抽样框总体容量也不相同;第二,此抽样框所包含的单位信息会随时间的变化而发生改变,使得分层抽样的层规模发生变化;第三,此抽样框的前期总体规模信息及抽取样本信息已知,而后期总体规模信息及抽取样本信息均未知,需要通过抽样进行推断。本文讨论的基于总体动态变化所构造的抽样框是前后两期抽样框中总体容量、总体单元和单位特征同时变化的情况。

为了进一步说明动态总体变化,用图1模型结构(图中图形个数无代表含义)直观表示此抽样框。按照抽样框中单元重复出现的情况,本文抽样框可以分为三种类型:第一,两个抽样框之间不存在重叠的部分;第二,两个抽样框之间存在包含关系;第三,两个抽样框都存在重叠部分。图1仅表示第三种类型的抽样框,也就是新生率、消亡率同时存在,抽样框包含了重叠区域ab,因此,使用事后分层复合抽样方法将抽样框在第t期与第t+1期总体及获取样本的情形描述如图1所示。其中,“○”表示在第t期第一层抽到的样本;“□”表示第t期第二层抽到的样本;“△”表示第t期第三层抽到的样本;“●”表示在第t+1期第一层抽到的样本,“■”表示在第t+1期第二层抽到的样本;“▲”表示在第t+1期第三层抽到的样本。由于第t期抽样框St中单位在第t+1期抽样框St+1其存活状态和目标变量的水平都有可能发生变化,抽样框St中空白区域标记为“○”、“□”、“△”是抽样框St+1各层中无法观察和匹配到的消亡样本,同时,抽样框St+1空白区域标记为“●”、“■”、“▲”的样本是在抽样框St中各层无法匹配到的新生样本,而重叠区域的样本则为存活样本。需要注意的是,虽然第t+1期抽取的部分样本在第t期依然存活,由于目标变量水平的变化,其样本可能存在着层级的变动。

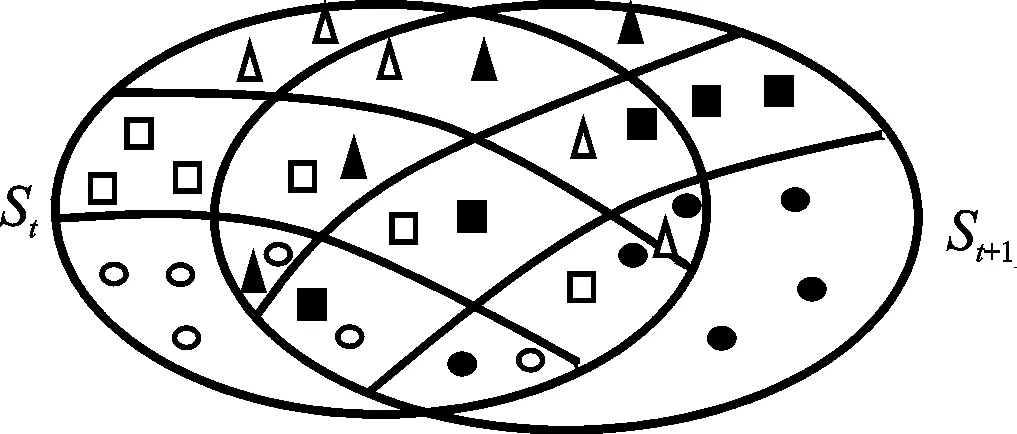
图1 抽样框内总体动态变动的模型结构

在固定抽样框覆盖不完整或无法及时更新的情况下,诸多调查采用将两个或两个以上的抽样框组合得到一个能够覆盖总体信息的多重抽样框。由于市场竞争加快,总体的特征变动速度较快,使得企业名录框变动较大,金勇进等在对规模以下工业调查的研究中使用多重抽样框进行样本选取,但是实际的应用中仅仅使用多重抽样框仍然无法解决实际问题[11]。本文基于总体容量、总体单元和单位特征同时发生变动的情形下,依据两个相邻时期的抽样框内各层所抽取的样本存在关联性的特点,通过事后分层复合抽样方法获取新生样本、消亡样本及存活样本的估计,从而实现对总体目标变量的抽样估计。为了描述该抽样方法,本文中使用的符号及其释义如表1所示。

表1 全文使用的符号及注释

本文设计的事后分层复合抽样方法采用以下抽样操作流程:第一步,依据抽样框St采用一次分层抽样,确定各层第t+1期抽样样本,能够在第t+1期被调查到的样本称为存活样本,未被调查到的样本称为消亡样本,得到消亡率的估计值及其存活样本目标变量的观测值;第二步,依据总体中抽取存活样本的目标变量观测值进行事后分层处理,重新划分分层标准;第三步,采用未知抽样框情况下随机抽样方法获取一定数量的二次抽样样本,识别在第t期抽样框St中能够观察到的样本和未能观察到的样本,据此对总体新生率及总体容量N(t+1)进行估计,并对二次调查样本的目标变量水平进行观测;第四步,依据第一次和第二次抽样获得观测样本对总体目标变量水平进行事后分层复合估计。

三、总体总量估计量的构造

(一)总体容量的估计

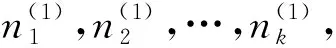
通过以上事后分层复合抽样方法可以实现总体抽样框中单位的消亡率与新生率估计值以及各个单位两期分层的变化。其消亡率与新生率的估计为:

(1)

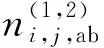
(2)

由消亡率、新生率和转移矩阵可以得到第t+1期各层总体容量的估计:

(3)

即:

因此,第t+1期总体容量的估计为:

(4)

其中,rj为第j层的总体容量变化率,有rj=1-qj-pj,j=1,2,…,k。由此得出t+1期动态总体规模的估计值。

(二)总体总值的估计及其优良性讨论

根据有关文献的H估计量和FB估计量的构造思路[1-3],在得到第t+1期各层总体容量的估计后,采用分离抽样框估计方法将抽样框St+1表示为ab区域和b区域的集合,并分别得到两个区域的目标变量观测值。利用这两个区域样本的复合估计各层总体目标变量值,最终联合各层子总体的总值估计得到总体总值的估计量,则第t+1期总体总值的估计量为:

(5)

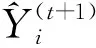
(6)

所以,第t+1期总体总值的估计量表达式可写为:

(7)

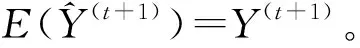
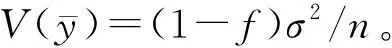
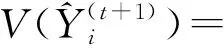
(8)

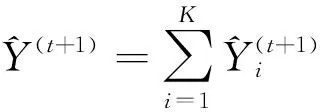
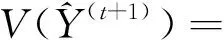
(9)

若采用第t期存活样本估计第t+1期总体总值,有:

(10)

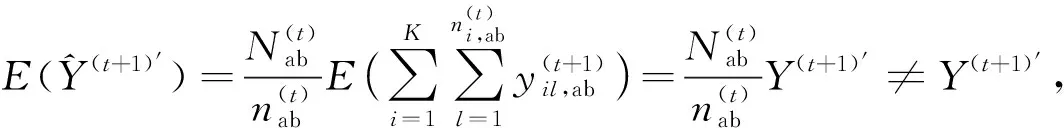
若采用事后分层抽样抽取第t+1期样本估计总体总值,有:

(11)

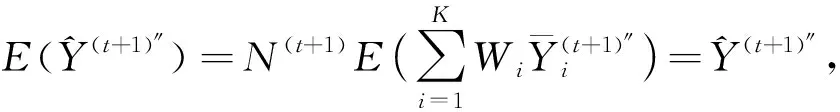
(三)复合估计最优调节系数的确定

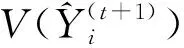
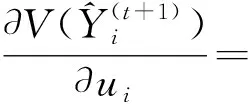
(12)

由式(9)得调节系数ui的最优取值为:

(13)

四、事后分层复合抽样方法的随机模拟

为讨论本文基于动态总体的事后分层复合抽样方法的优良性,采用蒙特卡洛方法对该理论进行说明。本次实验依据规模以下企业总体变化特点进行数据模拟,使其能够用于规模以下企业发展规律等研究。

本次随机模拟的设计过程如下:假定总体分为3层,即K=3。事后分层复合抽样方法的随机模拟主要分为三个步骤:第一步,生成抽样框。给定第t期总体均值,然后随机生成2 000个数,之后按照层内方差小,层间方差大进行分层,各层容量及均值分布如表2所示。给定各层消亡率值,系统随机删除第t期各层总体的部分样本单元即为各层消亡样本单元,删除后得到各层存活样本单元;对各层存活样本单元的值给予1.05左右的随机波动,同时给定新生率值,系统随机生成新的样本即为新生样本单元,结合新生样本单元和波动过后的存活样本单元得到第t+1期的总体单元,至此两期抽样框建立完成。第二步,进行抽样。在第t期的总体中按照等比例的样本分配在各层进行随机不放回抽样获得各层样本,将所抽取的各层样本与第t+1期的总体进行匹配,得到存活样本单元及其在第t+1期的观测值和各层的转移样本数;之后在第t+1期进行事后分层抽样,将所抽取的样本进行分层,与第t期总体进行匹配,得到新生样本单元,至此抽样过程结束。第三步,获取估计值。依据两次抽样获得的样本信息进行分析计算得到第t+1期的总体总值。

表2是数值模拟实验中第t期与第t+1期抽样框各项参数设置。为了保证抽样结果稳定,不因一次实验的随机性而引起较大偏差,对事后分层复合抽样过程重复450次实验。在每次事后分层复合抽样过程中,均计算样本企业经济水平总值和估计量方差,同时与第一次分层抽样所得的存活样本和第二次事后分层抽样所得样本的总值估计值进行对比,分析这三种不同抽样所得样本的总体总值与真实值的偏差。

表2 随机模拟实验的各项参数设置

表3是详细展示从450次事后分层复合抽样模拟结果中随机选取的两组估计值,通过两次抽样所获得的样本信息进行匹配,能够计算得到t期样本的消亡率、t+1期样本的新生率以及样本转移矩阵,通过式(4)和式(7),最终得到t+1期的总体容量和总体总值的估计。

表3 随机选取的两次事后分层复合抽样运行结果

本次随机模拟实验借助Python软件进行了随机模拟,给定各项参数计算得到第t+1期总体总值的估计值。分别采用第一次分层抽样存活样本估计总体总值和第二次事后分层抽样估计总体总值二种方法,与事后分层复合抽样估计总体总值进行对比。图2中对消亡率、新生率和总体容量的估计值与真实值进行了对比,其中消亡率的真实值为0.065,新生率的真实值为0.07,总体容量的真实值为2 012,可以看出各估计值的中位数与其真实值比较接近。图3为三种不同方法估计总体总值对比分析结果,可以看出基于动态总体的事后分层复合抽样估计总体总值的偏差分布在零轴附近,明显低于其他两种抽样方法估计总体总值的偏差,可见基于动态总体的事后分层复合抽样估计精度更高。此次实验结果表明在总体容量、总体单元和单位特征同时发生变动时,使用基于动态总体的事后分层复合抽样方法明显优于单次的分层简单随机抽样。

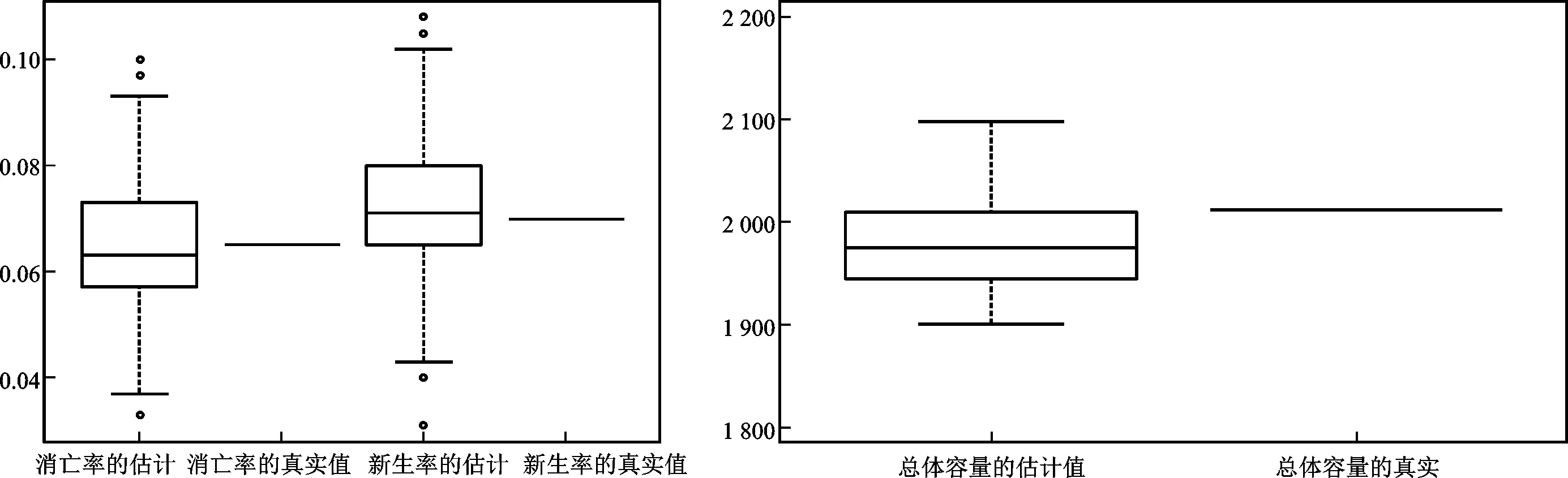
图2 消亡率、新生率和总体容量的估计值

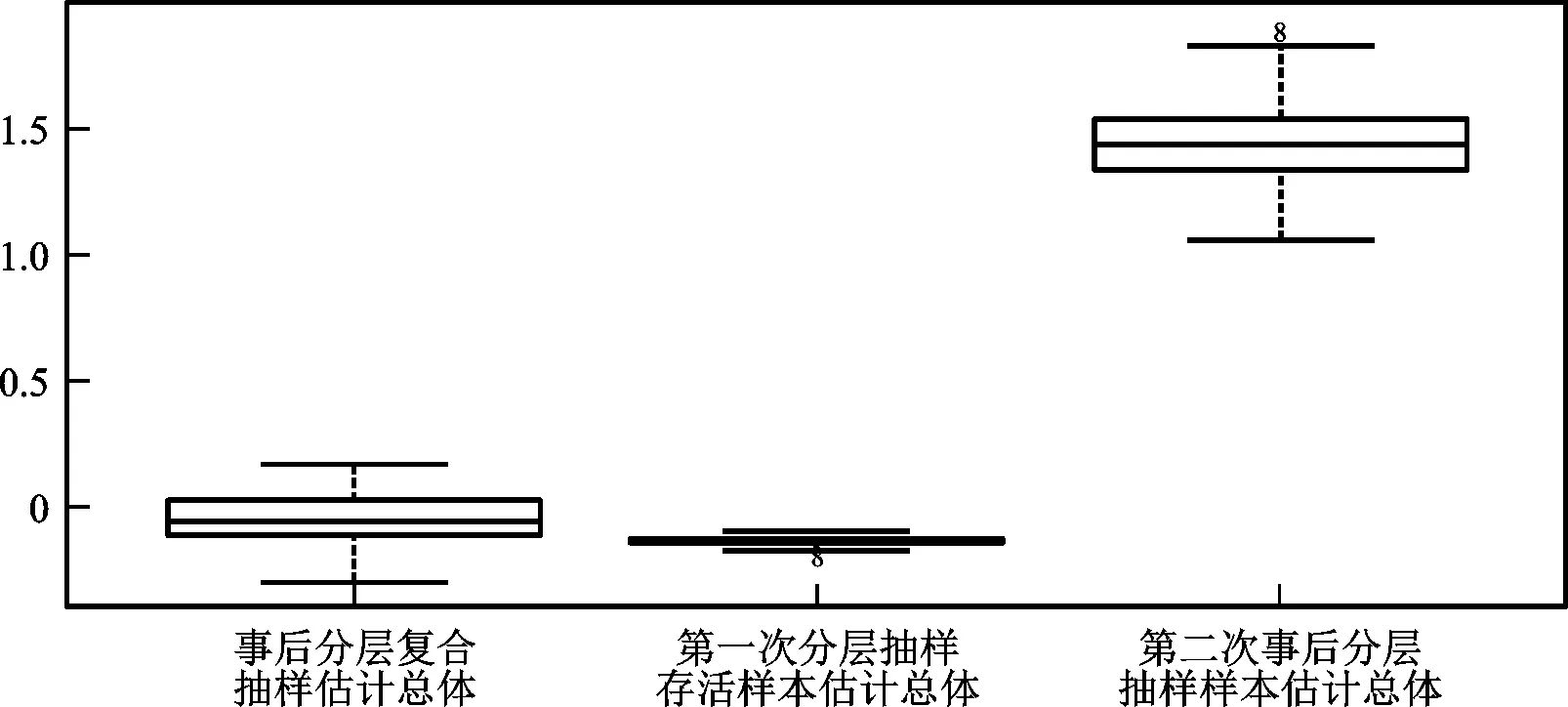
图3 总体总值估计值的偏差

五、结论

本文针对“三新企业”总体抽样框单位新生、消亡较为频繁,且单位目标变量水平变化较大的特点,研究了在总体容量、总体单元和单位特征同时变动条件下总体特征信息的估计,主要包括:对抽样框单位的新生率、消亡率、转移概率矩阵的估计,推断了动态总体的容量,同时采用事后分层抽样技术对抽样框单位进行层划分,据此设计了事后分层复合抽样方法以及构造第t+1期总体总值的估计量,并讨论了该估计量的优良性。实验结果表明,基于动态总体的事后分层复合抽样方法估计精度更高。本文仅讨论了第t+1期总体信息的估计,对事后分层复合抽样方法下方差最小及成本最优的样本分配研究仍需进一步讨论。