基于改进区间规划方法的内陆集疏运网络优化

2021-07-22王清斌都晓惠孟凡锋

铁道运输与经济 2021年7期

王清斌，都晓惠，孟凡锋

（大连海事大学交通运输工程学院，辽宁大连 116026)

0 引言

内陆集疏运网络是连接腹地城市与港口的纽带，可以为不同运输方式间的衔接提供平台，是进行一体化运输组织的关键。高效畅通的内陆集疏运网络对提高区域经济、加速港口发展具有重要意义。集装箱运输业的发展，使得内陆集疏运网络集疏运能力不足的问题日益凸显。

合理优化内陆集疏运网络，建立更合理的内陆集疏运网络体系，逐渐被学者们所关注。范厚明[1]通过设定需求情景表达不确定需求研究中转站选址问题；CARLOS[2]考虑需求和运输成本双重不确定性对中转站选址的影响；岳鑫[3]依据网络配流结果为集疏运网络可持续发展提出建议；潘静静[4]通过配流结果分析集疏运网络现状；孟晓雨[5]通过预测港口集疏运量对港口操作能力与铁路运输能力进行适应性分析；CAO[6]研究网络配流问题实现最小化集疏运成本及最大化客户满意度。目前，在选址问题研究中大多考虑需求的不确定性，而在研究网络配流优化时，大多忽略需求不确定性对配流结果的影响。基于此提出以需求不确定性为背景研究网络配流问题，由于区间数可以方便地表示不确定信息，选用区间数表示运输需求，并在此基础上优化集疏运网络。韩世莲[7]用区间数表示供需量研究不确定性运输问题；张相斌[8]用区间数表示成本，研究制造资源优化调度问题；CAO[9]运用区间规划处理不确定需求，将其应用于车辆路径问题中。

区间规划方法的使用具有局限性，目前主要应用于解决网络结构比较简单的问题中。内陆集疏运网络涉及节点较多、结构复杂，区间数的累加会导致配流结果的波动范围变大，为决策增加难度。因此，在传统区间规划方法的基础上，探索进一步合理处理区间数宽度的方法，以有效缩小求解结果的变动范围，降低决策难度。

1 模型构建

1.1 问题描述

集装箱运输市场的快速发展给内陆集疏运网络带来新的挑战。以集装箱多式联运为背景，根据内陆集疏运网络中货流分配情况，确定网络中不同资源承担的货流比例，通过改变网络中的资源配置情况改善网络配流结果，实现网络中各资源合理利用，进而提升网络集疏运能力。

内陆集疏运网络由节点和将节点进行连接的运输线路共同组成，为直观表示网络结构，构建内陆集疏运网络G= (E，V)。其中E表示节点集合，共包括以下3类节点：A表示具有运输需求的城市节点集合，A= {i}，i= 1，2，…，a；B为负责处理各种集装箱业务的中转站集合，B= {k}，k= 1，2，…，b；C为港口集合，C= {j}，j= 1，2，…，c。V表示运输线路集合，每条运输线路上具有不同种运输方式。W表示运输方式集合，W= {w}，w= 1，2，…，n。内陆集疏运网络示意图如图1所示。考虑城市运输需求的不确定性，城市货物可由某种运输方式直接运至港口或者经中转站中转后运往港口。各运输方式在中转站处发生衔接，节点间的运输任务要单独完成。构建以集疏运总成本最小为目标的网络优化模型，根据网络货流分配情况优化内陆集疏运网络。

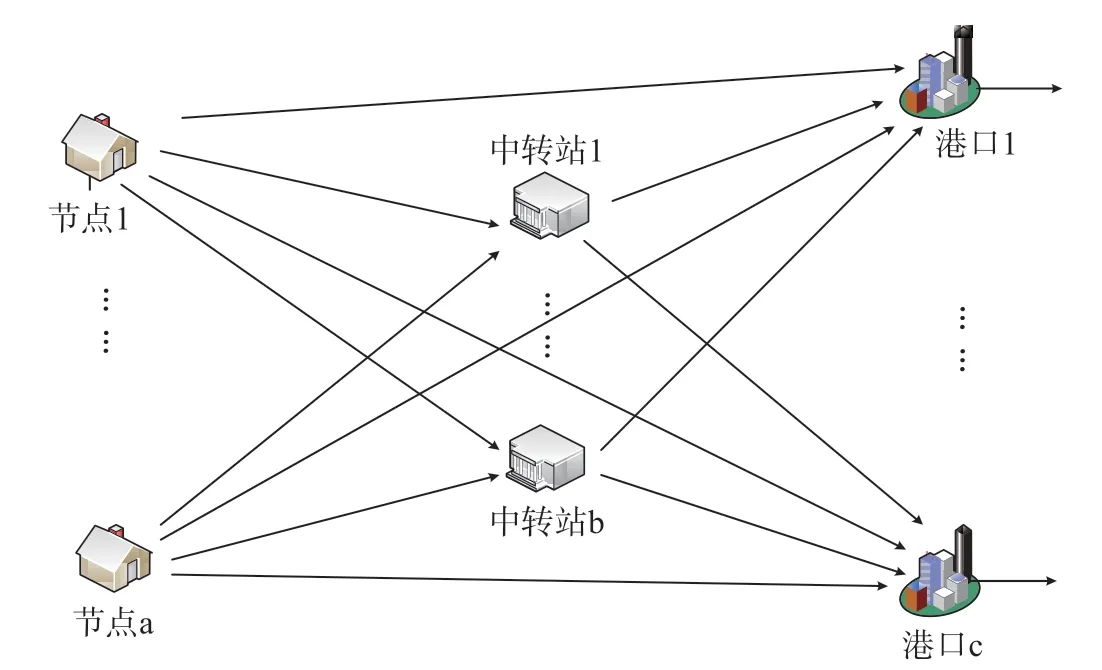
图1 内陆集疏运网络示意图Fig.1 Schematic diagram of inland collection and distribution network

1.2 改进区间规划方法

区间数可以方便地表示不确定信息，且具有客观性，选用区间数表示内陆集疏运网络不确定性运输需求。区间数的宽度直接影响求解结果的变动范围，内陆集疏运网络涉及多个节点、不同运输方式，网络结构复杂，各节点运输需求量的累加会导致求解结果变动范围增大，为此提出改进区间规划方法以缩小求解结果的变动范围，降低决策难度。改进区间规划方法将需求区间进一步细分构建需求等级，在此基础上建立鲁棒优化模型，使改进后方法更适用于内陆集疏运网络优化问题。内陆集疏运网络建设投资大、周期长，鲁棒优化模型综合考虑所有需求等级，使得求解方案在不同需求等级下均具有较好的性能，以此为基础优化内陆集疏运网络更具现实意义。

使用传统区间规划方法时，节点i运输需求不确定性用区间数表示，改进区间规划方法将区间数进一步细分为n +1个区间：，[xi1，xi2)，…，，每个细分的区间代表不同的需求程度，用Di表示，给定的需求程度为1，的需求程度为n +1，即Di= 1，2，…，n +1。将同一时间段内陆集疏运网络节点发生需求量大小的总体水平叫做需求等级，根据所有节点的需求程度之和为网络中具有运输需求的节点总数量)的大小来划分，需求等级集合S，S= {s}，s= 1，2，…，m。由历史数据可计算不同需求等级发生概率qs。综合考虑不同需求等级，建立鲁棒优化模型，使所求配流方案在不同需求等级下均适用，以此为基础研究网络配流情况，实现网络优化。

1.3 网络优化模型构建

网络优化模型的构建分为2个阶段，第1阶段求出每种需求等级下的内陆集疏运网络最小集疏运成本，第2阶段求出综合考虑所有需求等级时的内陆集疏运网络货流分配情况。

第1阶段以每种需求等级下内陆集疏运网络集疏运成本最小为目标，以网络中各资源配置实际情况为约束建立内陆集疏运网络优化模型，求出每种需求等级下成本最小值，具体如下。

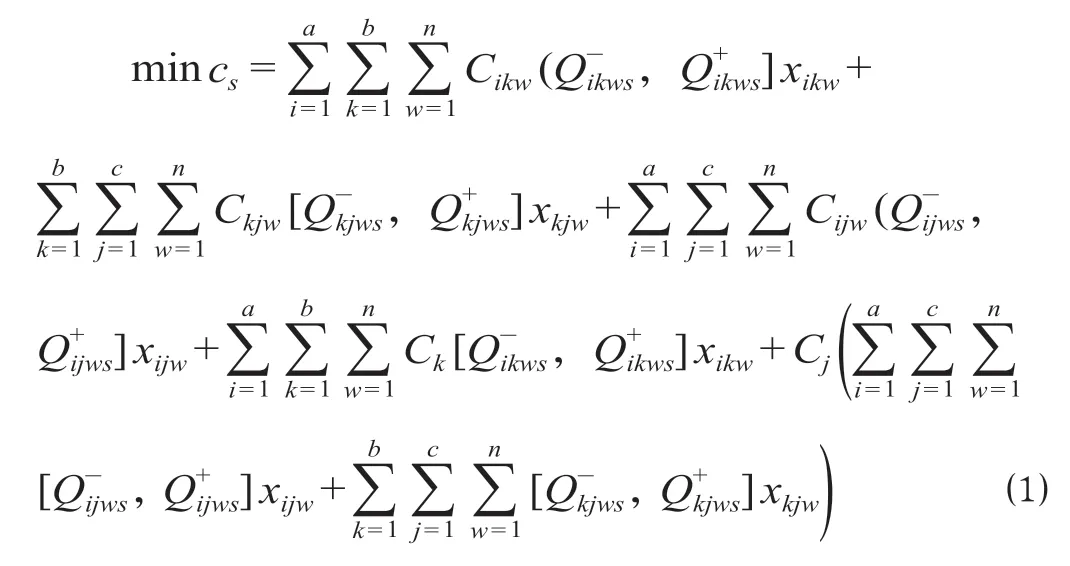
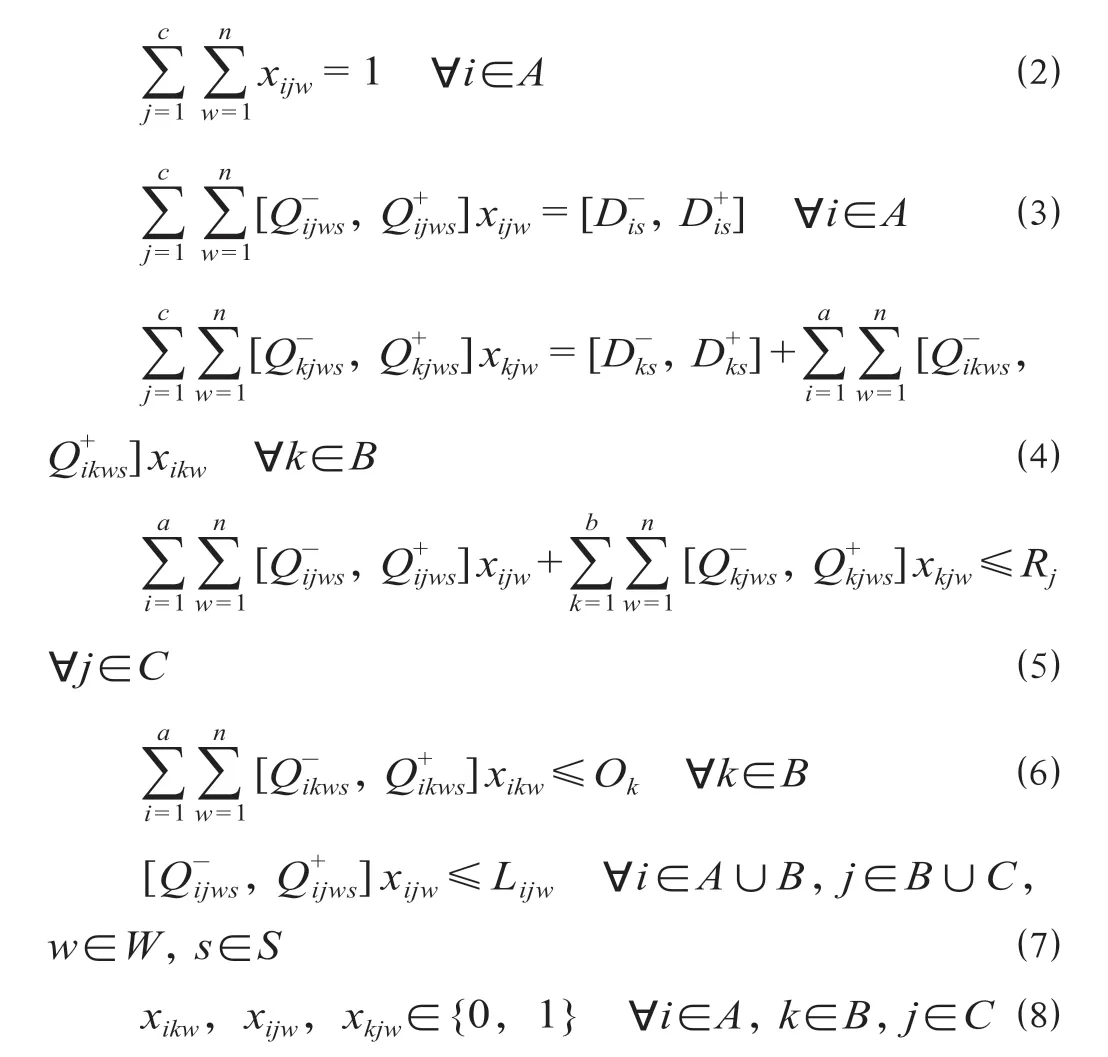
式中：cs为只考虑s需求等级时的最小成本，元；Cikw，Ckjw，Cijw分别表示从节点i到节点k、从节点k到节点j、节点i到节点j选择w种运输方式的单位运输成本，元/TEU；，分别表示s需求等级下通过w运输方式从节点i运到节点k、从节点k运到节点j、从节点i运到节点j的货运量区间，TEU；Ck表示中转站k单位中转成本，元/TEU；Cj表示港口j单位操作成本，元/TEU ；表示节点i在需求等级s下的需求运量区间，TEU；表示中转站k在需求等级s下的需求运量区间，TEU；Rj表示港口操作能力，TEU；Ok表示中转站操作能力，TEU；Lijw表示节点i到j选择w方式的运能，TEU。xijw为决策变量，

公式(1)为只考虑1种需求等级时的最小成本，由运输成本、中转站操作成本以及港口操作成本组成；公式(2)为2节点间运输线路约束，表示运输需求节点i的运输路径与运输方式均只能选一种；公式(3)为货运量与运输需求量约束，表示节点i的运输需求量需被满足；公式(4)为中转站货流量守恒约束，表示中转站到港口货运量等于城市到中转站的货运量与中转站自身货运量之和；公式(5)为港口操作能力约束，表示城市到港口货运量与中转站到港口货运量之和不超过港口自身操作能力限制；公式(6)为中转站操作能力约束，表示各城市到中转站货运量之和不超过中转站操作能力限制；公式(7)为运输方式运能约束，表示货运量不能超过运输方式的运能；公式(8)为决策变量约束。

第2阶段综合考虑第1阶段中所有需求等级建立鲁棒优化模型，以找到在每种需求等级下均适用的内陆集疏运网络货流分配方案。第2阶段网络优化模型以网络中各资源配置实际情况为约束条件，具体公式为公式(1)至公式(8)；以最小化内陆集疏运网络期望成本及每种需求等级下偏离最小成本的偏移量为目标函数，公式为

式中：θ为目标函数值，元；qs为不同需求等级发生的概率；cs为改进区间规划方法求得的配流方案在s需求等级下的成本，元；r为解的鲁棒度量因子，使模型求解的结果在各需求等级下都接近最小成本；是由第1阶段求得的每种需求等级下集疏运成本最小值，元。

1.4 模型确定性转化

网络优化模型中带有区间数，区间数无法直接进行比较和计算，需要将区间规划模型转化为确定性模型，引入区间数Ai的表示方法为

式中：Ai表示区间数，表示Ai的下限，表示Ai的上限。mAi为Ai的中点，反映Ai的大小；wAi为Ai的半宽，反映Ai的不确定程度。mAi，ωAi的计算公式为

网络优化模型中带有区间数的模型可分为带有区间数的目标函数、带有区间数的不等式约束以及带有区间数的等式约束3类。在Jiang[10]的研究基础上，对模型确定性具体转化过程如下。

（1）目标函数的转化。运输需求量是区间数，目标函数的计算结果也是区间数，目标函数的转化综合考虑区间数的中点和半宽，以找到最优目标函数区间，具体转化过程为

式中：f(x)为目标函数，是1个区间数；α为决策者对决策方案不确定性的敏感程度；mf(x)为目标函数的中点；ωf(x)为目标函数的半宽。

（2）不等式的转化。带有区间数的不等式，实际上是比较2个区间数的大小，由于区间数无法直接进行比较，其中区间数的可能性程度可表示1个区间数大于或小于另一个区间数的可能程度，可将带有区间数的不等式转化为可能性程度进行比较。对给定2个区间数A1和A2，区间数A1≤A2的可能性程度表示为

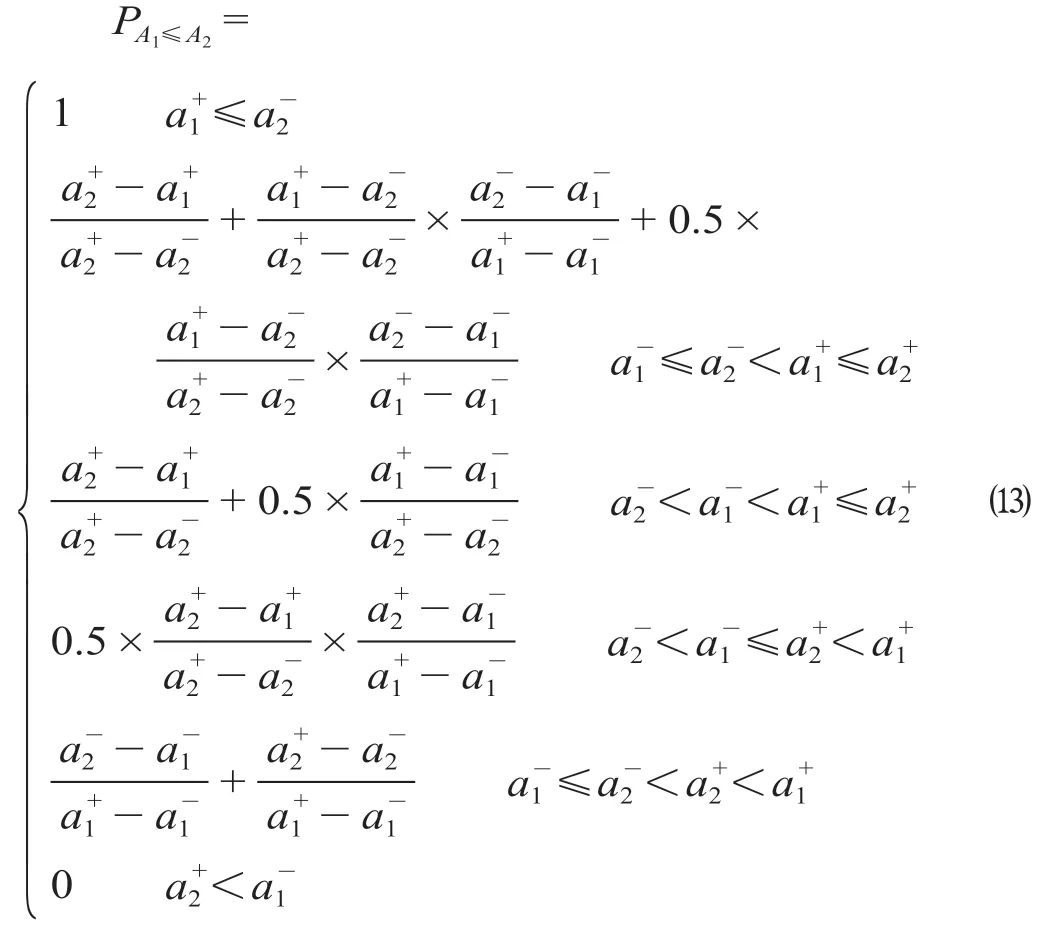
结合公式(5)至公式(7)，区间数A2退化成实数，即，公式(13)可简化

不等式约束的转化过程即是将不等式约束转化为不等式成立的可能性程度，当不等式成立的可能性程度不小于给定值μ0时则原不等式成立，具体为

式中：A1x≤a2为不等式约束，其中A1，a2为参数，x为决策变量，A1是区间数，a2是实数；P(A1x≤a2)表示不等式成立的可能性程度，μ0为不等式成立的满意度，μ0∈ (0，1)；是由公式(14)推导出的P(A1x≤a2)的计算方法。

（3）等式的转化。等式约束确定性转化过程为先将带有区间数的等式转化成不等式组，再按照不等式的转化方法转化成确定性模型，带有区间数的等式转化过程为

式中：A1，A2为2个区间数；x为决策变量。

2 算例分析

2.1 数据收集及处理

算例选取大连港和营口港及其主要腹地城市所组成的内陆集疏运网络，验证模型及改进区间规划方法的有效性。共选取东北地区33个城市，其中哈尔滨、长春、沈阳因其地理位置优势设为内陆集装箱中转站，内陆集疏运网络中运输方式包括公路运输和铁路运输2种，东北地区内陆集疏运网络分布图如图2所示。

图2 东北地区内陆集疏运网络分布图Fig.2 Distribution map of inland collection and distribution network in northeast China

（1）运输需求处理。改进区间规划方法在传统区间规划方法的基础上进一步处理运输需求区间以使得求解结果更准确。具体运输需求处理步骤为：①划分运输需求区间确定需求程度。计算各城市节点周运输需求均值，根据均值将区间划分为：[0，，，分别用1—4依次表示4个区间的需求程度Di。②根据需求程度构建需求等级。网络中共包括33个城市节点，需求程度之和区间范围为33≤。由各城市节点周运输值确定该城市节点周需求程度，根据同一周内所有城市节点需求程度之和构建运输需求等级，具体如下：需求等级s1为；需求等级s2为；需求等级s3为；需求等级s4为。4个需求等级代表内陆集疏运网络集装箱运输需求量由低到高。③计算每种需求等级发生概率。根据每种需求等级发生的次数确定概率，由历史数据统计每类需求等级发生的频率分别为0.2，0.4，0.3，0.1。求解时取每种需求等级下发生次数最多的1组数据计算。

（2）参数值收集。网络自身参数包括不同运输方式的运输成本、中转站操作成本、港口操作成本、运输方式运能、中转站操作能力及港口操作能力，网络自身参数参考既有文献[11]获取。改进区间规划方法应用时所涉及参数包括决策者对决策方案不确定性的敏感程度α、解的鲁棒度量因子r及不等式的满意度μ0，给定α= 0.5，r= 0.1，不等式满意度μ0取0.9。

2.2 结果分析

选取改进区间规划和传统区间规划2种方法，分别对需求上下限构成的区间构建不同需求等级并进行求解，得到2个配流方案，由传统区间规划方法求得的配流方案为传统区间规划方案，由改进区间规划方法求得的配流方案为改进区间规划方案。对比2个配流方案成本的期望、后悔值的方差、各资源承担货流比例情况，证明改进区间规划方法的改进效果。

计算2个配流方案在每种需求等级下的成本值，由于区间数无法直接比较，运用公式(12)对成本值进行确定性转化，结合需求等级发生概率可计算出成本的期望及后悔值的期望和方差，得到2个配流方案成本期望及后悔值期望和方差对比表如表1所示。由表1分析可得：①改进区间规划方案期望成本较低。使用传统区间规划方法时需考虑所有节点的最大需求值，而实际所有节点同时发生较大需求值的概率趋近于0，改进区间规划方法通过构建需求等级能更好反映内陆集疏运网络实际运输需求情况，从而得到成本更低的配流方案。 ②改进区间规划方案后悔值方差小。改进区间规划方法结合鲁棒优化模型，鲁棒优化可以增强解的鲁棒性，从而减弱后悔值的波动性，使得任一需求等级下均可获得接近最小成本的配流方案。

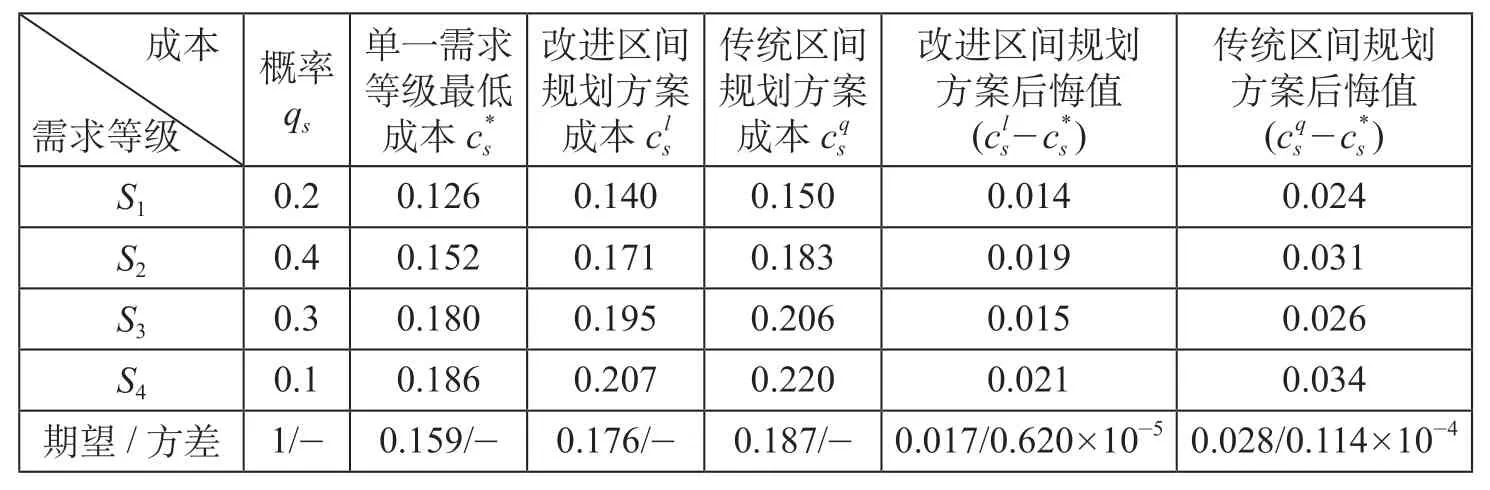
表1 2个配流方案成本期望及后悔值期望和方差对比表亿元Tab.1 Comparison of cost expectation, regret value expectation, and their variances between two distribution schemes

对比2个配流方案下内陆集疏运网络不同资源承担的货流比例，得到2个配流方案各资源承担货流比例对比表如表2所示。比较货流比例的区间数宽度，改进区间规划方案下的货流比例变动范围小于传统区间规划方案，传统区间规划方法需求区间宽度较大，节点较多，导致配流结果变动范围较大，作为决策依据参考价值较小；改进区间规划方法通过进一步细分需求区间构建需求等级有效缩小了求解结果的变动范围，降低决策难度。从总体上看该内陆集疏运网络中，直达所占货流比例较高，中转较少，现有内陆集疏运网络对中转站利用不足；铁路所占货流比例较低，现有内陆集疏运网络对铁路利用不足。决策者可从以上2个方面优化内陆集疏运网络，以实现内陆集疏运网络运营水平的提升。

表2 2个配流方案各资源承担货流比例对比表 %Tab.2 Comparison of freight flow proportion corresponding to each resource between two distribution schemes

改进区间规划方法通过构建需求等级，可以更准确描述内陆集疏运网络运输需求情况，从而获得成本更低的配流方案；通过进一步细分需求区间，缩小需求区间宽度，使得货流比例的变动范围更小，有效降低决策难度。因此，在改进区间规划方案的基础上优化内陆集疏运网络更具合理性。

2.3 敏感性分析

改进区间规划方案可以更好反映内陆集疏运网络货物流动情况，在其基础上进行敏感性分析，达到优化网络的目的。敏感性分析，是通过分析模型中的运能及节点操作能力对配流结果的影响，其中节点操作能力包括中转站操作能力和港口操作能力，再通过对比配流结果变化，为解决现有内陆集疏运网络中的问题提供解决方案和建议。

2.3.1 运能敏感性分析

对比释放运能前后网络配流方案的变化，列出配流方案发生改变的节点，得到释放运能前后运输方案对比表如表3所示。由表3可以直观看出运输方案发生改变的节点，运输方式均是由公路变成铁路，说明该网络公路运能充足，铁路运能不足。可以通过释放表3中各路段铁路运能以加大对铁路的利用。

对比释放运能前后内陆集疏运网络各资源货流比例变化，得到释放运能前后各资源承担货流比例变化表如表4所示。分析表4可以得出，加大铁路运能后，铁路承担的货流比例增加，原网络中铁路运输利用较少的原因是铁路运能不足；直达中转货流比例变化不大，选择中转的货物量较少；大连港货流比例增加，原网络中大连港操作货物量较少的原因之一是大连港距离各城市节点较营口港更远，导致公路运输成本较高，而大连港铁路运输较营口港更为便利，增大铁路运能可使大连港货流比例增加。

表3 释放运能前后运输方案对比表Tab.3 Comparison of transportation schemes before and after releasing transport capacity

2.3.2 节点操作能力敏感性分析

节点操作能力包括港口操作能力和中转站操作能力，分别释放港口操作能力、中转站操作能力，对比网络货流比例变化，得到释放节点操作能力货流比例表如表5所示。释放港口操作能力后，发现营口港的货流比例上升，近年来营口港因其自身的地理位置优势，一直保持高速发展的状态，表5表明操作能力不足是营口港的短板，加大营口港的操作能力可使营口港货流比例进一步上升；释放中转站操作能力后，中转的货流比例上升，表明现有网络中转量较少的原因是中转站操作能力不足；在总中转量增大情况下，哈尔滨、长春中转比例上升，长春尤为明显，表明该网络应首先加强对长春中转站的建设，以充分发挥中转站的中转作用。

3 结束语

在考虑运输需求不确定性的内陆集疏运网络优化问题中，提出改进区间规划方法处理运输需求，该方法为不确定性问题的处理提供了新思路。算例结果表明：改进区间规划方法可求得成本更低的配流方案，且不同资源承担的货流比例变动范围更小，可有效降低决策难度。改进区间规划方法使得将区间数应用于复杂的网络优化问题中成为可能，可以为后续研究提供理论帮助。同时通过优化网络资源配置情况改善内陆集疏运网络货流分配结果，实现网络中各资源充分利用，从而提高内陆集疏运网络集疏运能力，为网络未来发展提供决策依据。