基于非线性优化的激光雷达在线标定算法

杨 超，李天剑，胡 欢，黄 民

(北京信息科技大学 机电学院，北京 100192)

0 引 言

近些年来，基于激光雷达定位的自动引导车(automated guided vehicle，AGV)逐渐运用于各个不同领域。通过激光雷达作为主传感器进行精确位姿估计的前提是预先知道传感器的外参配置。对于一个机器人系统而言，标定外参通常是机器人工作前的首要步骤[1]。

在机器人领域，关于外参标定的研究一直是热点所在，尤其是即时定位与建图技术(simultaneous localization and mapping，SLAM)技术发展火热以后。关于激光雷达的外参标定研究较多的包括相机与激光雷达的联合标定等，黎云飞等提出的基于fmincon法的单线激光与单目相机外参标定法[2]，降低了标定计算量。姚文涛等提出了一种自适应摄像机与激光雷达联合标定算法[3]，简化了标定过程。韩栋斌等提出了基于多点匹配的三维激光雷达外参标定方法[4]，减小了标定初值对标定结果的影响。Zhe Gao等提出了利用简单的平面测量方法在硬件要求较低情况下对2D激光雷达的标定方法[5]。祝飞等通过融合多种棋盘格约束的面阵相机与线激光约束，减少了激光噪点对标定结果的影响，提升了标定精度[6]。Miguel Oliveira等利用ROS框架提出了一种多模型的外参标定算法，同时标定多个外参并简化了标定流程[7]。在利用里程计的激光标定方面，Andrea Censi曾对此问题展开研究，提出了一种里程计与激光雷达的联合标定方案，该方案解决了对机器人内参与外参的同时标定，该方案在外参解决上采用了闭式求解。目前，对于7×24 h工作的移动机器人而言，其激光外参需要进行实时在线标定，以保持其精度的准确性，上述标定方案通常都需要辅助以特定标定板等工具进行标定，同时受限于环境(对标定环境有严格要求)，基本都是离线标定方案，不利于机器人进行在线标定，另外目前也存在标定精度不够等问题。

针对上述问题，基于里程计的激光标定算法，本文提出了一种利用非线性优化的求解方式，该方法将标定问题建模为观测与预测之间的非线性模型，能够利用非线性最小二乘方案进行求解，通过误差最小化，可以得到较为精确的标定值。

1 模型构建

使用2D激光雷达的移动机器人主要考虑其在2D平面中的运动，忽略机器人的形态大小，单纯以点来描述机器人，那么在二维平面中描述机器人的位姿需要3个自由度，设位姿为p，则

p=(x,y,θ)

其中，x,y代表机器人在对应坐标系下的位置，θ描述机器人的姿态，即其绕垂于x,y平面的旋转角，称之为偏航角。

机器人的姿态观测可通过传感器获得，本文以传感器为2D激光雷达以及码盘为主的差速运动机器人为研究对象，通过轮式码盘可得到机器人的里程计数据，即机器人本体的位姿变换。而2D激光雷达亦可通过帧间匹配得到雷达在世界坐标系下的位姿变换。激光雷达与机器人本体间存在静态的位姿变换，即所要求解的标定外参。根据二者之间的关系得到非线性数学模型，通过对非线性问题求解，即可得到激光雷达外参。

1.1 非线性优化模型构建

图1描述了机器人在一定间隔时间t内机器人各坐标系之间的运动关系，假设机器人从t1时刻运动到t2时刻，图中O1代表t1时刻的码盘航迹推算得到的世界坐标系下里程计位姿，即机器人车体位姿，O2为t2时刻对应的世界坐标系下里程计位姿，To代表里程计航迹推算所得机器人在t1到t2时刻对应坐标变换。S1表示t1时刻激光雷达观测所得激光雷达在世界坐标系下位姿，S2表示t2时刻激光雷达观测得到激光雷达在世界坐标系下位姿，Ts代表激光雷达观测所得雷达在t1到t2时刻之间的坐标变换。Tx表示激光雷达在机器人坐标系下的静态坐标变换，即所求外参对应的坐标变换，该值为静态值，不会随机器人运动而发生变化。

图1 机器人坐标系间运动关系

根据上述对应关系，目前已知在不同时刻下激光雷达及里程计在世界坐标系下的对应位姿，而根据欧式变换，可进一步获得在t2时刻机器人在t1时刻里程计坐标系下的坐标变换，首先将t1时刻世界坐标系下里程计位姿转换为欧式变换矩阵

(1)

其中，Oθ1，Ox1，Oy1分别为机器人里程计在t1时刻对应的位置参数与位姿参数。To1代表从世界坐标系到t1时刻机器人坐标系的坐标变换。

将t2时刻世界坐标系下里程计位姿转换为欧式变换矩阵

(2)

To2代表从世界坐标系在t2时刻机器人坐标系的坐标变换。

根据欧式群变换理论，可获得t2时刻机器人到t1时刻机器人的坐标变换为

To=To1To2

(3)

同理，可获得t2时刻激光雷达在t1时刻对应激光雷达坐标系下坐标变换为

Ts=Ts1Ts2

(4)

根据式(3)、式(4)求解得到坐标变换To、Ts，以及激光雷达到机器人坐标系下的坐标变换Tx，可得到t2时刻激光雷达到t1时刻里程计坐标系下的坐标变换，该坐标变换可通过两种方式得到

T1-2=TxTs

(5)

T1-2=ToTx

(6)

将这两个等式连列，消去T1-2，则得到下面方程

TxTs=ToTx

(7)

将式(7)稍作化简，则得

(8)

式(8)即所求数学模型，该数学模型为非线性化数学模型。

1.2 里程计位姿求解

差速运动机器人的里程计运动学模型依赖固连于连杆两端的双电机通过速度差分求得，如图2所示，其对应机器人速度及角速度为

图2 差速运动学模型

(9)

(10)

其中，vL与vR分别为左右轮轮速，d为轮间距。

假设机器人在t1时刻位姿为p(x，y，θ), 在理想情况下，通过航机推算，t2时刻机器人的位姿为

(11)

而实际运用中，机器人的运动收到噪声的影响，真实的速度与测量得到的速度存在一定误差。将这种误差描述为以0为中心的有限方差的随机变量[8]。实际的速度及角速度表达如下

(12)

其中，εα1v2+α2w2,εα3v2+α4w2为方差为α1v2+α2w2，α3v2+α4w2， 均值为0的误差变量，α1～α4为机器人特定的误差参数。

因此，对应的运动学航迹推算模型为

(13)

1.3 激光雷达位姿求解

激光雷达的位姿求解有多种方式，SLAM技术中大量涉及关于激光传感器的定位问题，主流的激光雷达位姿求解主要通过帧间匹配的方式，即通过匹配相邻两帧激光或关键激光帧的重合部分，求解得到激光雷达的位姿变换。而匹配方式也包含多种方法，包括原始的迭代邻近点匹配[9]，融合速度估计的VICP[10]匹配以及点线匹配等。目前，在匹配方式中，点线匹配方式效果较好，本文选用点线匹配来进行雷达位姿求解。

点线匹配算法又称点线迭代临近点匹配，由于两帧激光在扫描过程中，激光点并不会完全进行点到点重合，该算法将原始的点到点匹配优化为点到线直接的匹配，用点去匹配最邻近的直线段，提升了激光帧间的精度[11]，如图3所示。其算法流程如下：

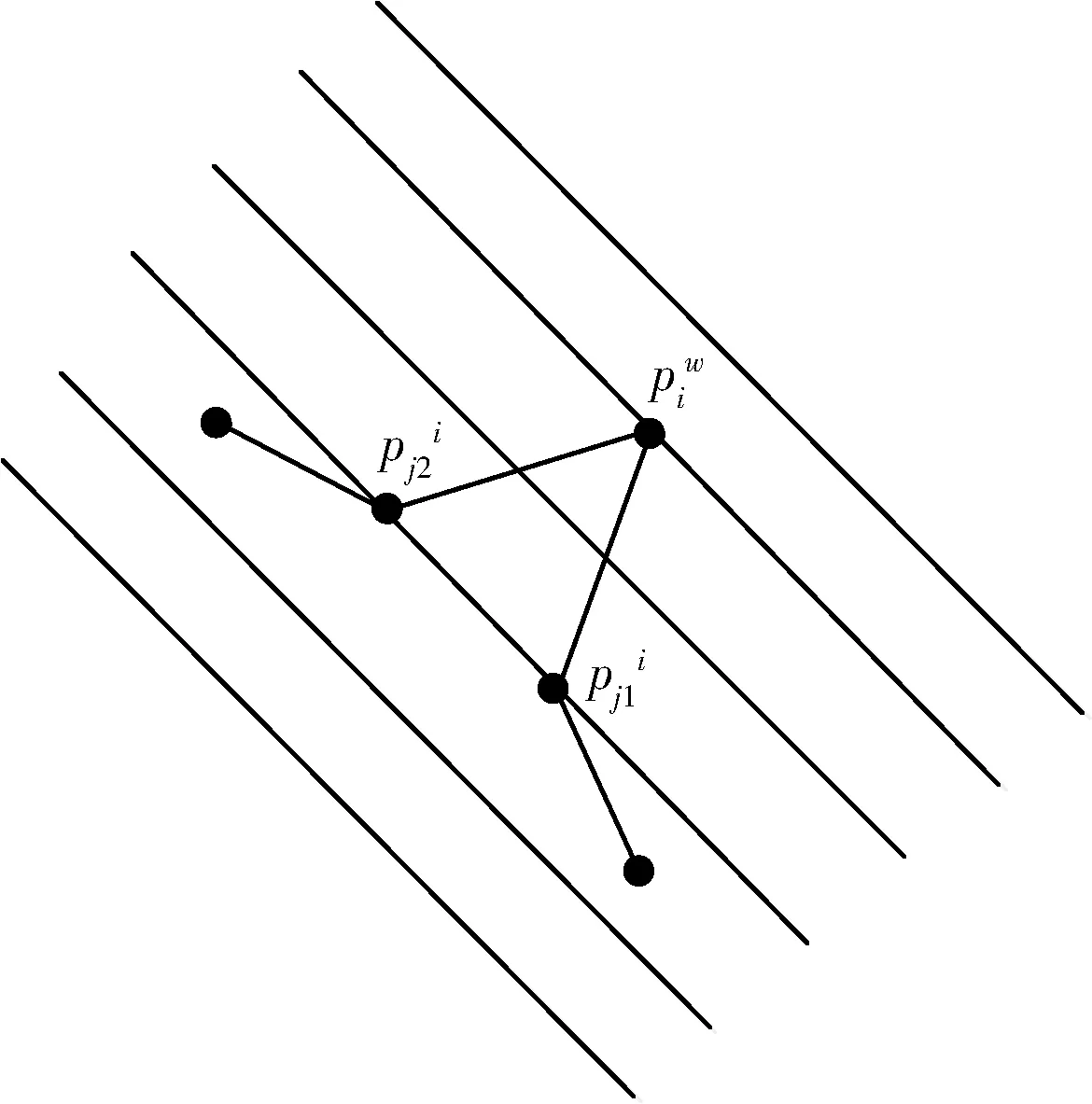
图3 点线匹配

(1)列出两帧激光之间的变换关系，将当前激光帧中激光点用pi表示，将参考帧中激光点用piw表示，则激光点之间的变换关系为

(14)

其中，Δx,Δy表示激光点从pi到piw的位置变换，θk表示激光点从pi到piw的位姿变换。

(2)计算激光帧从当前变换到参考帧坐标系后，激光点pi到临近两个激光点所组成的线段之间的最近距离；

(3)通过最小二乘，将此问题表达为非线性优化问题，通过最小化残差，求解得到两帧激光之间的坐标变换，其优化模型为

(15)

其中，i∈{1,2,…,n}，n为当前激光帧与参考激光帧所匹配得到的激光点数量，pj1i为参考激光帧中距离点piw最近的激光点，niT为过激光点piw且垂直于线段pj1ipj2i的单位法向量。

2 外参求解

2.1 实际考虑

根据以上所述，已经求得激光雷达位姿变换Ts，里程计位姿变换To，可将二者带入式(8)中，由于该式为非线性数学模型，无法通过线性方式之间求解。设所解Tx如下

由于Tx为坐标变换，则x7=x8=0，x9=1，x1=x5，x2=-x4则Tx的形式变换为

且存在约束x12+x22=1， 代入式(8)后可发现该方程存在解析解，可通过拉格朗日乘子将该问题转换为闭式解形式。但这种解析解仅适用于理想情况，在实际情况中，里程计中速度与角速度的获取本身带有高斯误差，而在实际场景中，机器人要面临不同的路面情况，其左右轮会存在不同程度打滑，这都是不可忽略的误差。其次，激光雷达的波束模型同样带有噪声，实际中的一面直墙在激光雷达的观测中不尽然是一条直线，如图4所示，同时在帧间匹配过程中，存在误匹配的情况，这些都会造成激光雷达位姿求解的误差。这些误差最终都会造成解析解的标定精度，Andrea Censi曾将此闭式解问题通过反复迭代标定来提高标定精度。

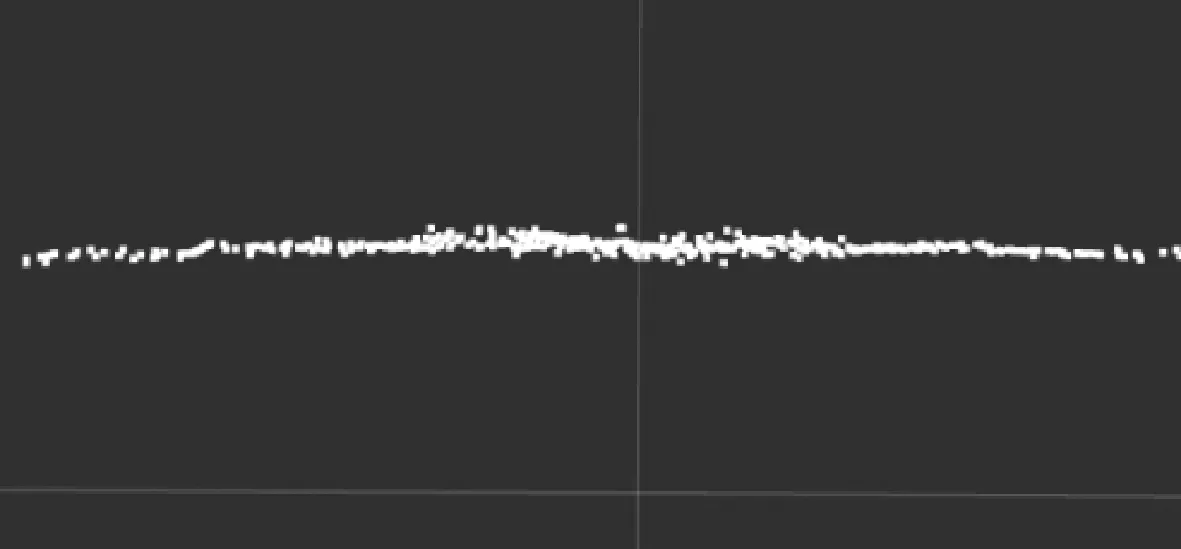
图4 激光噪点

本文提供另一种求解方式，直接将此问题作为优化问题进行求解。

2.2 非线性求解

考虑将问题转化为优化问题，将式(8)转化为如下数学模型

eT=Ts-T′o

(16)

e=z′-o′x

(17)

其中，e为位姿残差，z为激光雷达在世界坐标系中位姿，o′x为里程计位姿通过外参求得激光雷达在世界坐标系中位姿，该问题可通过非线性最小二乘进行求解。

目标为最小化预测和观测的差，将里程计得到坐标变换转换得到的激光坐标变换作为预测值，将激光帧间匹配得到的坐标变换作为观测值，则

ei(x)=zi-fi(x)

(18)

zi为ti时刻激光观测位姿，fi(x) 为ti时刻里程计预测位姿，ei(x) 为ti时刻位姿残差。假设误差服从高斯分布，设其对应的信息矩阵为Σi， 因此该观测值误差的平方定义为

Ei(x)=ei(x)TΣiei(x)

(19)

因此，非线性最小二乘的目标函数为

(20)

对误差函数进行线性化

ei(x+Δx)=ei(x)+Ji(x)Δx

其中，雅克比矩阵Ji为映射函数对状态向量x的导数，其值为

因此，目标函数转化为

(21)

其中， F(x+Δx) 为关于变量Δx的二次函数，其极值可通过令其关于Δx的导数为0求解得到

(22)

令x=x+Δx, 然后不断迭代，直到收敛。

2.3 其它考虑

(1)由于激光雷达帧间匹配对初值要求较高，在初值较为不准确的前提下有可能在解算时陷入局部最优值，因此将里程计得到位姿变换作为初值进行帧间匹配。

(2)里程计采样过程中，轮子可能存在打滑，造成里程计数据的不准确，因此在优化之前，首先进行滤波，去除一定百分比的较大误差。

(3)为进一步提高精度，采用二次优化的方式，即一次优化完毕后，将第一次优化所得外参作为初值带入进行二次优化，得到较为精确的外参。

(4)算法实现以ROS[12]系统为框架，ROS(robot operating system)为开源机器人操作系统，其利用节点/话题通信方式以及功能包开发方式加快了机器人软件的开发进程，其中，ROS中便捷的TF转换与监听功能能够帮助进行里程计及激光雷达数据同步。

整体算法流程如下：

(1)订阅激光雷达数据/scan；

(2)通过订阅/tf话题得到每帧激光雷达对应时间里程计位姿；

(3)通过两帧里程计位姿得到相邻里程计位姿差 d_point_odom；

(4)判断d_point_odom运动距离间隔与角度间隔是否足够大，若不满足返回第(1)步；

(5)通过给定外参初值，将d_point_odom转换为激光坐标系下位姿tmpPose，并作为初值传递给帧间匹配PL-ICP；

(6)通过帧间匹配，得到相邻激光帧位姿差d_point_scan；

(7)通过角度偏差进行滤波；

(8)构建非线性优化模型目标函数，添加残差；

(9)达到预定优化数量后，进行迭代优化求解，得到一次标定参数；

(10)将所得标定参数作为新一次优化初值进行二次优化，返回第(1)步；

(11)达到优化数量后，通过距离偏差进行滤波，迭代求解后，得到最终外参。

3 实 验

本文使用搭载双激光雷达的差速运动机器人为实验对象，其雷达型号为SICK TIM561。

(1)机器人选择：本文使用机器人为中型AGV，该机器人其左后方与右后方分别放置一枚SICK TIM561激光雷达(图5)。同时安装有双电机及轮式编码器，为差速运动机器人。

图5 机器人及激光雷达

(2)环境选择：考虑到帧间匹配的准确性，为保证标定准确，标定环境倾向于选择结构化环境，本文使用木板搭建方形结构环境(图6)，这种环境能够保证帧间匹配(点线匹配)的准确性，环境大小为(3m×3m)。

图6 标定环境

(3)激光雷达：本文选用激光雷达型号为SICK TIM561，激光雷达扫描频率为15 Hz角度分辨率为0.33度，扫描范围为0.05 m～10 m，扫描角度范围为270°，该激光雷达可在一帧激光内得到721束激光束，影响该激光的扫描精度因素包括扫描距离，由于激光本身在观察过程中存在噪声，当激光距离障碍物过近或过远时，其噪声相对较大，在实验中，需首先对激光进行预处理滤波，排除较近与较远距离数据。激光在机器人运行过程中会存在畸变问题，尤其是激光帧率较小(5 hz ～10 hz)，其畸变随机器人运行速度提高而增大，在标定过程中，应慢速运行。另外，在扫描反射比低于10%(深色物体)时，因光本身的性质，激光的扫描范围会相应减小，最远距离为8 m。

(4)数据提取：在进行优化前，需提取优化数据，包括激光帧间匹配数据以及里程计的变换位姿。由于轮子打滑等因素的影响，过短时间内，里程计的误差将会对里程计位姿造成显著影响。因此，在数据提取时，应尽量选择稍长时间段内的数据。

(5)轨迹选择：激光外参标定包括两个部分：位置参数与姿态参数，单纯的平移变换无法标定位置参数，单纯的旋转变换无法标定姿态参数。机器人在运动过程中需包含平移与旋转轨迹。

3.1 外参标定波动值

在激光雷达外参真值无法实际获得的情况下，通过多组实验的外参波动大小验证算法有效性。通过在所搭建结构化环境中，进行多次实验，实验结果外参见表1。

表1 机器人左右激光外参标定值

从标定结果可以看出，左激光外参在x方向波动值在1 mm 以内，y方向波动值在2 mm以内，theta值波动范围在0.01弧度以内，右激光x方向波动值在2 mm以内，y方向波动值在2 mm以内，theta值波动范围在0.01弧度以内。

3.2 双激光雷达验证

SICK TIM561激光雷达的扫描角度范围为270°，在rviz中观察标定运动状态下左右激光的点云匹配程度如图7、图8所示。

图7 左右激光点云匹配(1)

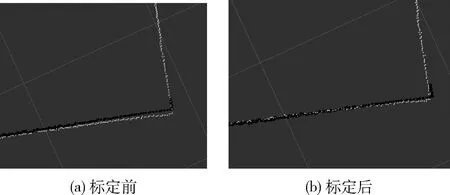
图8 左右激光匹配(2)

图中黑色激光点云为左激光捕获点云，白色为右激光捕获点云。左图为标定前，即初值分别为(-0.335，0.36，2.36)(-0.335，-0.36，2.36)，左右激光帧捕获点云无法严格重合，标定后，取标定参数为(-0.3375，0.350，2.34)(-0.330，-0.360，-2.37)，其左右激光点云重合程度优于标定前。

3.3 对比实验

与闭式求解方式精度对比：录制相同数据包，分别通过两种算法对同一数据包进行处理，处理结果见表2。

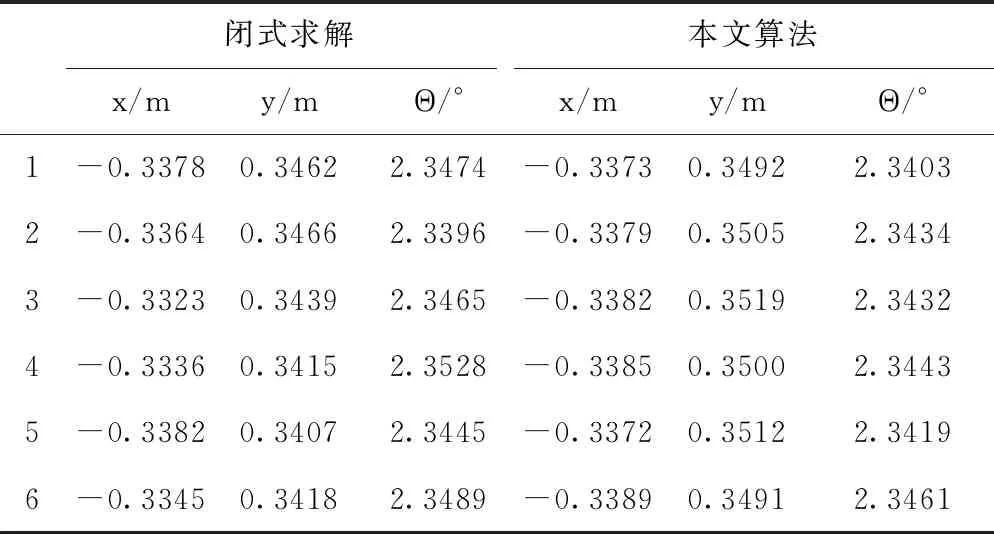
表2 算法对比

在相同数据包下，闭式求解x方向波动为6 mm，y方向波动为6 mm，theta值波动为0.02弧度，与本文算法相比，本文算法精度优于闭式求解方式。

3.4 实际项目场景应用

本文算法适用于不同场景，图为在实际工厂中进行在线标定后标定效果，非结构化环境下标定效果如图9、图10 所示。

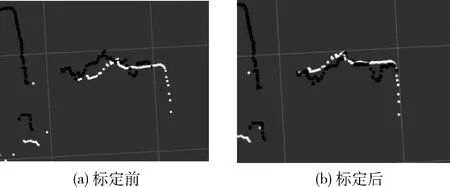
图9 实际工厂环境标定效果(1)

图10 实际工厂环境标定效果(2)

在非结构化环境中，激光噪点较多，激光标定精度不如结构化环境，但标定前后左右激光仍可达到较好的匹配程度，算法可有效运用于非结构化环境。

3.5 激光外参标定在SLAM中应用

SLAM技术在定位过程中，对传感器外参精度有较高要求，不精确的激光外参会对机器人定位效果产生较大影响，进而影响建图效果，图11为使用本文算法标定前后，利用图优化SLAM算法进行建图效果。

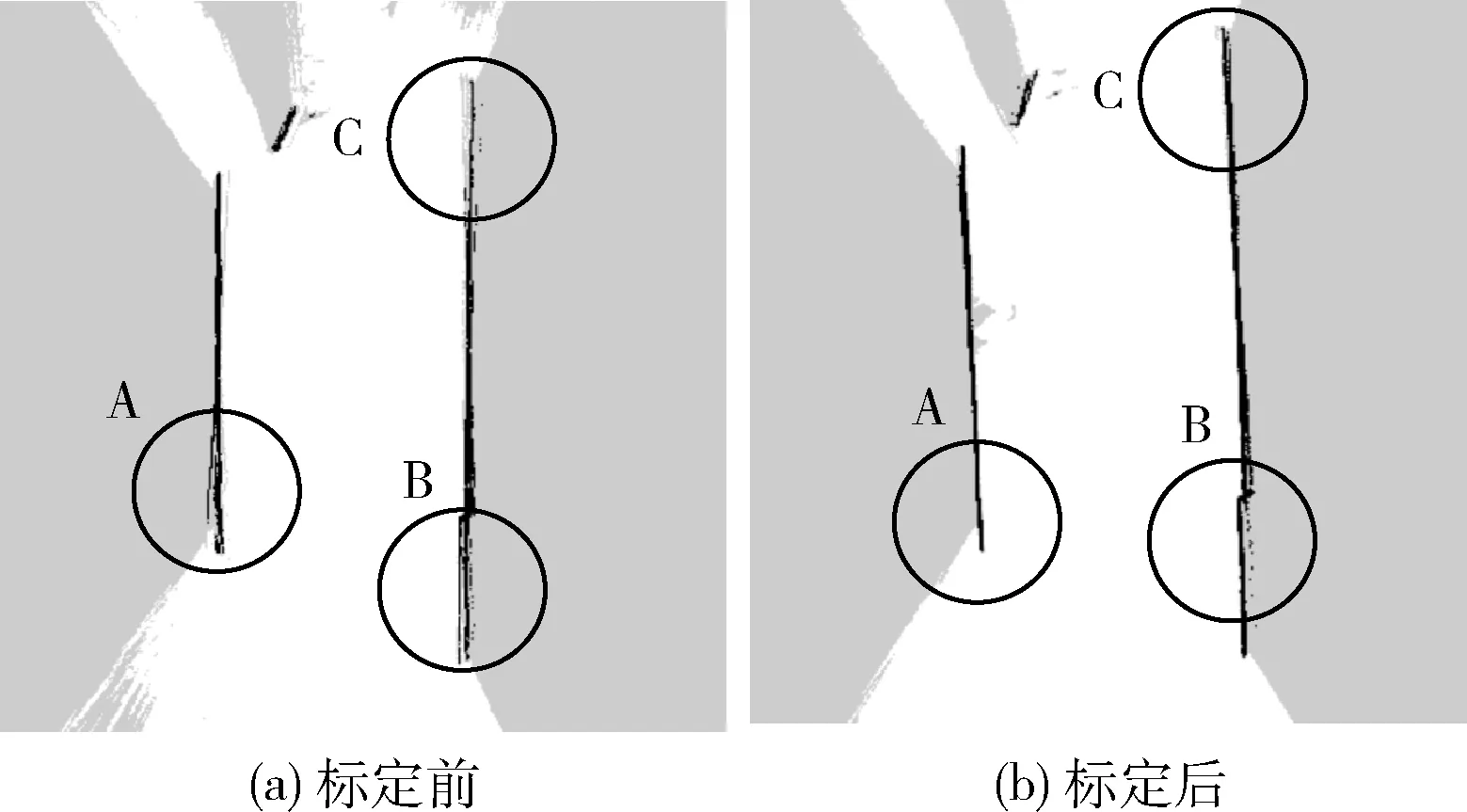
图11 标定前后SLAM效果

从图11可看到，标定前，SLAM建图存在重影问题，在A、B、C这3处位置存在不同程度重影，标定后，重影问题明显减小。

4 结束语

针对以轮式里程计以及激光雷达为主要传感器的差速机器人的激光标定问题，提出了一种基于优化方式的标定算法，算法将标定问题转换为预测与观测之间的非线性优化模型，标定过程中，对标定轨迹有一定要求，需包含平移与旋转，就标定环境而言，不仅适用于结构化环境，同样适用于非结构化环境，结构化环境中的标定结果优于非结构化环境。通过实际实验验证，通过双激光雷达点云匹配，标定后点云重合程度明显优于标定前，在结构化环境中，该算法的标定波动值在x、y方向误差保持在2 mm以内，角度误差保持在0.01弧度以内，优于闭式求解方式。在实际工厂环境标定实验中，该算法标定结果能够有效提高点云匹配精度，在SLAM应用方面，标定后激光建图精度明显优于标定前。