车联网中自适应联合计算卸载资源分配算法

林 峰，罗铖文+，丁鹏举，蒋建春

(1.重庆邮电大学 通信与信息工程学院，重庆 400065；2.重庆邮电大学 电子信息与网络工程研究院，重庆 400065；3.重庆邮电大学 自动化学院，重庆 400065)

0 引 言

随着C-V2X中各种计算密集型和对延迟敏感的应用兴起，给计算资源有限的车辆带来了巨大挑战[1]。移动云计算(MCC)资源丰富，但是距离车辆较远，会产生巨大的传输时延和能耗[2]。将计算下沉到MEC服务器，使得时延和能耗更低[3]。文献[4]提出一种云辅助的移动边缘计算卸载策略，结合遗传算法以时延和能耗最小化为优化目标。文献[5]使用强化学习，为降低计算时延，将任务卸载到本地、MEC、远端云服务器。文献[6]提出了一种联合计算卸载策略，将计算任务分别在MEC、空闲车辆，和本地计算。文献[7]提出一种节能的卸载策略，在远端云协助下优化MEC系统中的卸载选择和资源分配来最大程度地降低成本。目前工作中，同时考虑时延和能耗的前提下对多辆车并发卸载进行研究的较少，以及计算平台并未得到充分利用。在上述工作的基础上，本文提出一种自适应的联合计算卸载资源分配算法，首先，该算法考虑多辆车并发卸载计算任务的场景，在满足最大时延约束下，该算法能自适应得到每辆车卸载到本地、远端云服务器、MEC服务器、空闲车辆的最优任务比例，同时对MEC的计算资源做最优分配。通过实验仿真与其它算法相比，验证所提算法具有最小系统总成本。

1 系统模型

1.1 网络模型

为了尽可能利用所有的计算资源来降低系统总成本，考虑了4种计算卸载方式。如图1所示，卸载车辆的计算任务可以在本地计算，可以卸载到当前RSU下的空闲车辆Vidle计算，可以卸载到配备有MEC服务器的RSU上计算，也可以通过蜂窝网卸载到远端云服务器计算。远端云服务器的计算资源丰富，但是车辆卸载任务到远端云服务器的通信时延，能耗会很高，RSU上配备的MEC服务器离车辆近，通信时延低，但是计算资源有限。空闲车辆计算能力较弱，但是通信时延较低。

图1 网络模型

假定多辆车同时卸载任务，定义当前RSU覆盖下有计算任务需要卸载的车辆集合为V={v1,v2,…,vn}， 每辆车都有一个计算任务需要卸载，对应的任务集合为S={S1,S2,…,Sn}, 空闲车辆的集合为C={c1,c2,…,ck}。 假设车辆上传链路的信道是瑞利信道模型[8]。

车辆vi与BS之间的上传/下载的数据速率为

(1)

车辆vi与空闲车辆、MEC之间上传/下载的数据速率为

(2)

1.2 任务模型

1.3 计算模型

1.3.1 本地计算模型

(3)

(4)

其中，Pi表示车辆vi的设备功率。

1.3.2 MEC计算模型

(5)

(6)

(7)

(8)

(9)

1.3.3 云计算模型

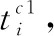
(10)

(11)

(12)

(13)

(14)

其中，Pcloud表示远端云服务器的设备功率，PBS表示基站的发射功率。

1.3.4 空闲车辆计算模型

(15)

(16)

(17)

(18)

(19)

其中，Pidle表示空闲车辆的设备功率。

2 问题建模

在本节中，将多个车辆的任务卸载和MEC的计算资源分配建模为多约束优化问题，在本研究中考虑的是多天线的卸载方式，故4个时延不是简单的相加关系，而是取它们中最大的时延。所以由前一节可以得到联合卸载的总时延T，总能耗E，定义联合卸载系统的成本为H

(20)

(21)

H=γ·T+(1-γ)·E

(22)

其中，γ为时延权重系数，(1-γ)为能耗权重系数。可根据移动服务的需求及移动设备的状态来设置。例如，当运行时延敏感型移动服务时，可以适当增加γ的值。

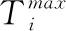
(23)

C1表示车辆vi确定把任务Si要卸载到本地，MEC服务器，远端云服务器，空闲车辆的任务比例相加为整个任务；C2表示完成每辆车的任务的时间不应超过最大容忍时延；C3表示能卸载到空闲车辆的最大数目；C4表示为每个车辆分配的计算资源不能超过MEC服务器的总资源；C5表示为车辆任务分配的计算资源总和不能超过MEC服务器的总资源。

3 算法设计

目前，许多研究采用智能算法解决优化问题。本文选择改进的粒子群算法，即带压缩因子的粒子群算法(PSO-X)[10]。由于本文的目标函数有等式和不等式约束，所以在PSO-X基础上，提出矩阵编码方式，和粒子修正算法，并在目标函数基础上加上罚函数进行约束条件的处理。本文改进的粒子群算法流程如图2所示。

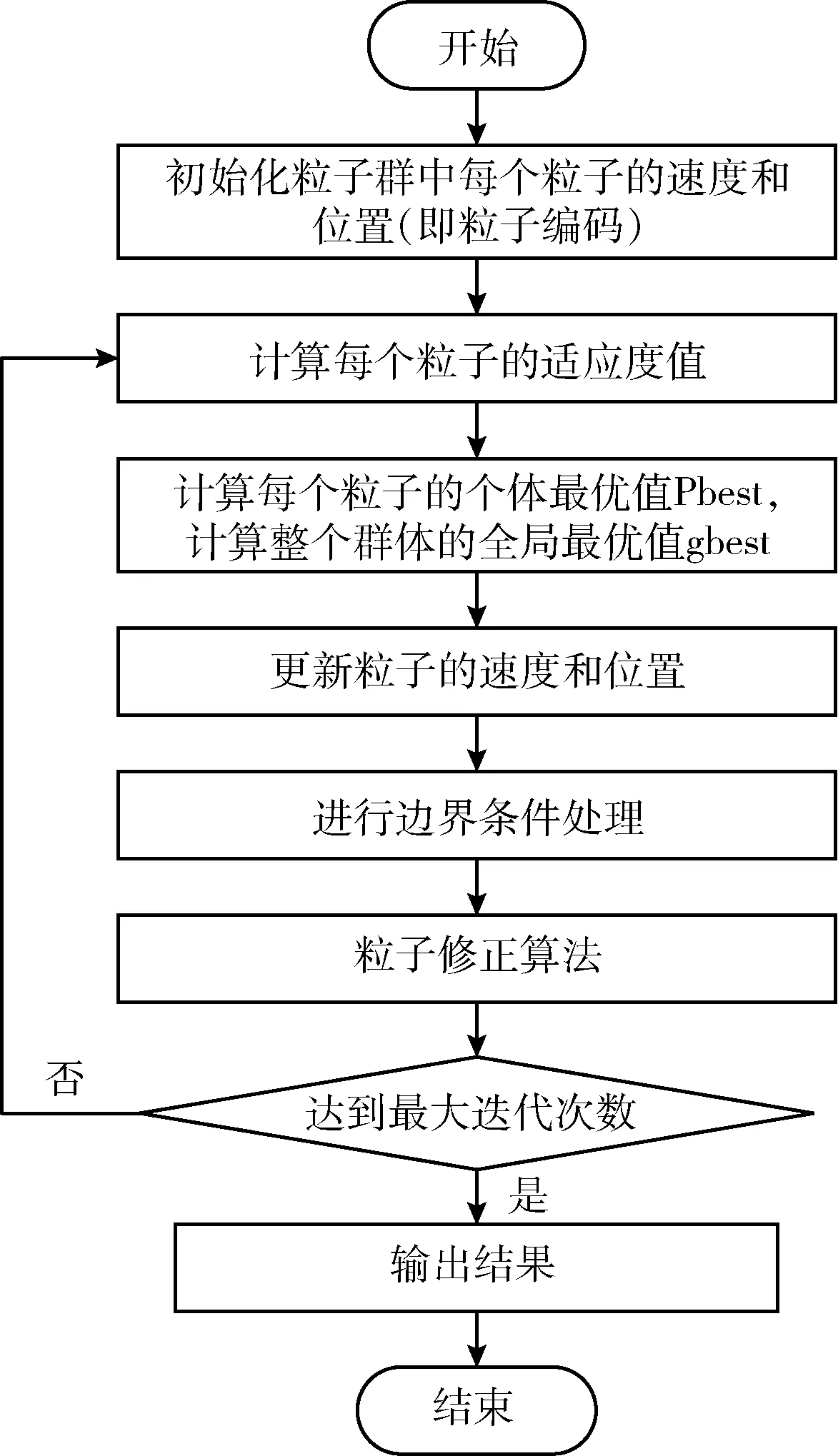
图2 改进粒子群算法流程

3.1 粒子编码

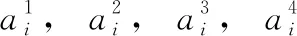
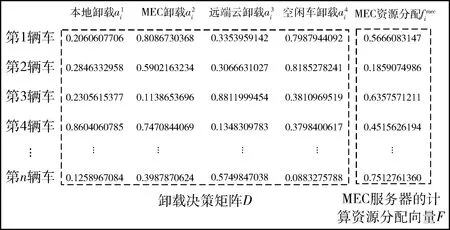
图3 粒子编码矩阵

3.2 粒子修正算法

从图3可以看到，初始化的粒子编码矩阵每一行的前4列相加不为1，不满足约束C1。粒子编码矩阵的第5列相加不为1，不满足式约束C5。粒子编码矩阵的第4列大于0的个数超过了当前空闲车辆数，不满足约束C3。所以在本小节给出一种粒子修正算法来使得粒子满足式(23)的C1，C3，C5约束条件。C4约束在初始化和边界处理之后，一定会满足，C2用罚函数法进行处理。

假设当前RSU下有car辆车需要任务卸载，idlecar辆空闲车辆。粒子修正算法描述见表1。

表1 粒子修正算法

通过粒子修正算法后，粒子的编码矩阵如图4所示。可以看到粒子编码矩阵每一行的前4列相加为1，也就是每个车辆卸载到各个计算点的任务相加为整个计算任务。矩阵的第5列相加为1，表示当前RSU下为每个车辆分配的MEC计算资源之和等于MEC服务器的总资源，矩阵第4列大于0的个数等于2，表明当前只能为两辆车提供计算任务。

图4 粒子编码矩阵修正后

3.3 罚函数法构造适应度函数

罚函数法可以将约束优化问题转换为非约束优化问题。该方法通过创建两个约束函数，加入惩罚因子，然后将它们添加到约束优化问题的目标函数中创建惩罚函数[11,12]。

将式(23)中的C2改写为

(24)

当x≤0，是不进行惩罚的，只有当x>0时，才进行惩罚，所以惩罚函数为

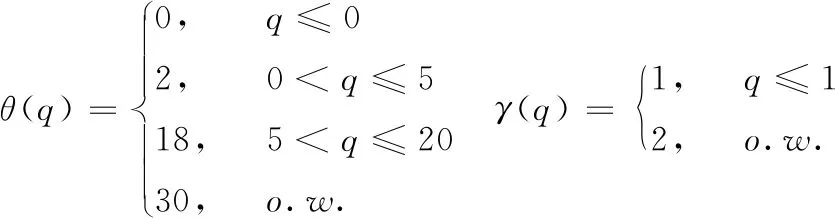
(25)

其中，q是相对约束惩罚函数，θ(q) 是分段赋值函数，γ(q)是惩罚指数。

适应度函数为目标函数加上惩罚函数

(26)

3.4 粒子速度与位置更新

在粒子群算法中使用约束因子去控制粒子行为以达到最终收敛[13]，不仅可以有效搜索不同的区域，而且能得到高质量的解。压缩因子法的速度更新公式为[14]

(27)

4 仿真结果与分析

在本节中分别对本文算法、All-Local算法、All-Mec算法、Random算法以及文献[6]算法进行仿真和对比。

All-Local算法：将任务全部留在本地进行计算。

All-Mec算法：将任务全部卸载到当前RSU配备的MEC服务器上进行计算。

Random算法：将任务随机的全部卸载到本地，MEC，远端云服务器，空闲车辆进行计算。

文献[6]算法：将整个计算任务分成3部分，分别在空闲车辆，MEC和本地计算。

改进的PSO-X算法的参数设置见表2，所提算法的相关仿真参数见表3。

表2 PSO-X算法相关参数

表3 仿真参数

图5展示了空闲车辆数对平均每辆车系统成本的影响，也就是对系统总成本的影响，从图中可以看到，随着空闲车辆数的增加，平均每辆车的系统成本呈下降趋势。其中，车辆数为16的下降趋势最大，车辆数为10的下降趋势最小。这是因为在RSU下车辆数较少时，每个车辆都能获得较多的MEC计算资源，空闲车辆的计算资源对降低系统成本的趋势较小。当车辆数增加时，所能获得的MEC计算资源减少，此时增加空闲车辆数,能较大的降低系统成本。

图5 空闲车辆数对平均每辆车系统成本的影响

从中可以看到平均每辆车的系统成本低于400，说明本算法能够在满足最大容忍时延的同时，最小化系统总成本。

图6展示了计算任务量对系统总成本的影响，并与其它4种算法进行了对比。可以看到，随着计算任务量的增加，5种算法的系统总成本也随着增加，本文所提算法的增加的幅度最小，并且系统总成本明显低于其它4种算法，约是All-Local算法的22.09%，All-Mec算法的38.66%，Random算法的27.8%，文献[6]算法的68.80%。

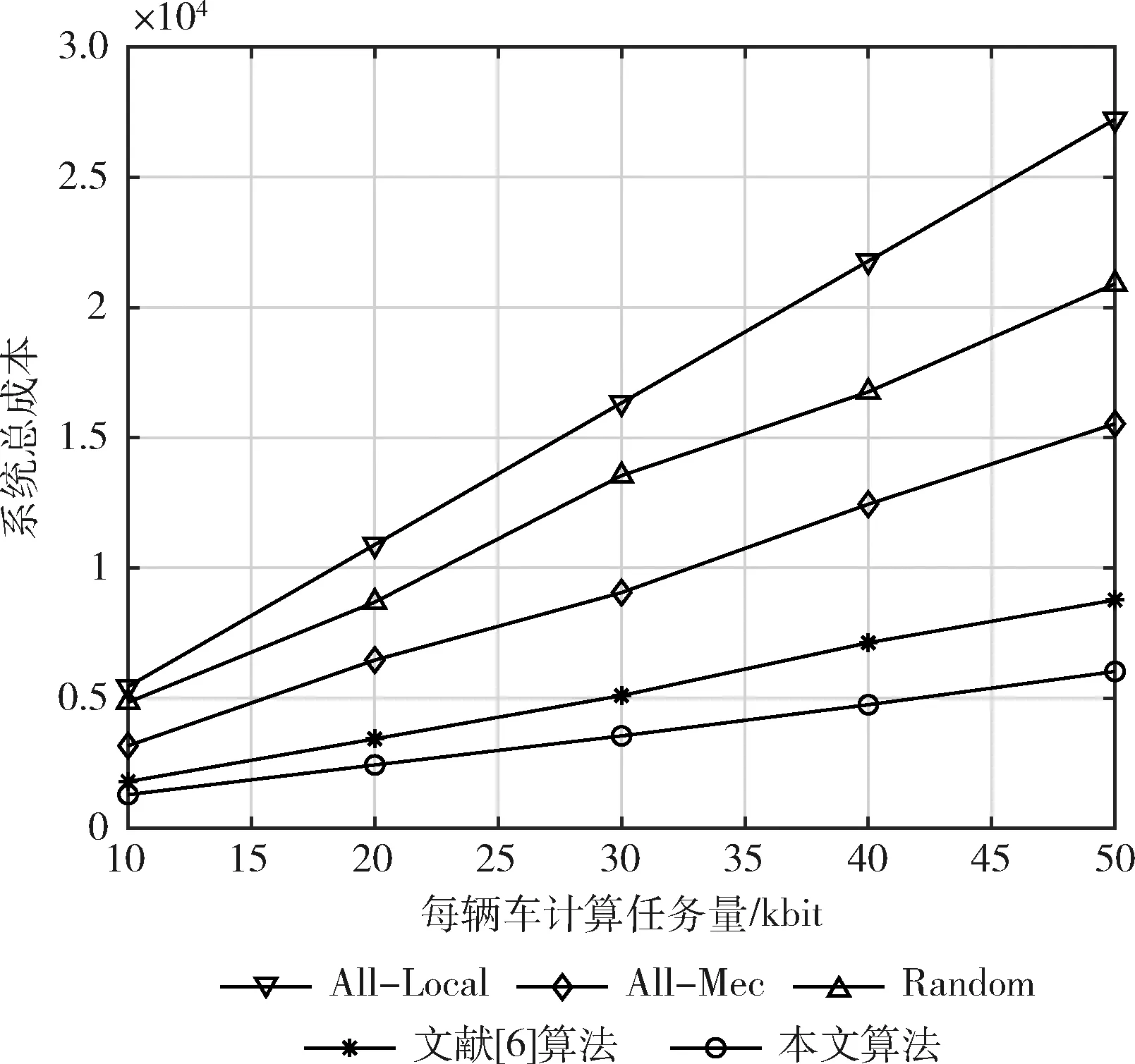
图6 计算任务量对系统总成本的影响

图7展示的是车辆数对系统总成本的影响，随着车辆数的增加，5种算法的系统总成本都呈现上升趋势。All-Mec算法在车辆数为20时出现突增，是因为当车辆数超过一定值时，导致MEC分配给每辆车的计算资源还没有本地高，所以会出现比本地计算的系统总成本还高。本文算法相比其它算法，具有最小的系统总成本。

图7 车辆数对系统总成本的影响

图8展示了带宽分配因子λ，ω，也就是带宽对系统总成本的影响，随着λ，ω的增加系统的总成本降低。因为当带宽增加时，传输时延降低，能耗降低。而且可以看到当ω一定时，随着λ的增加系统总成本的下降速度快。当λ一定时，随着ω的增加系统总成本的下降速度相比于前者较慢。是因为ω增加，也就是与BS之间的带宽增加，那么卸载到远端云的传输时延就会降低，卸载到远端云的任务量会自适应增加，而远端云的计算能力比MEC服务器强，所以比增加λ时的系统的总成本下降较快。

图8 带宽对系统总成本的影响

如图9所示，随着输出数据量的增加，除了All-Local外所有算法的系统总成本都增加。因为本地计算不存在计算结果的返回时延，所以All-Local算法的系统总成本保持不变，而其它算法的影响也较小，是因为只有卸载到MEC，远端云，空闲车辆才有结果返回时延，而计算结果的返回量相对较小，所以对系统成本影响不大。因此，在许多的论文中都是忽略不计的[15]。

图9 输出数据量系数对系统总成本的影响

5 结束语

本文为了降低C-V2X中计算任务的时延与能耗，提出一种自适应的联合计算卸载资源分配算法。所提算法相比之前的研究，综合考虑了每个车辆任务的大小、最大容忍时延、当前路边单元小区计算资源，网络带宽。并且能够根据当前RSU的任务数自动调整卸载平台和最优卸载比例，在获得卸载比例的同时对MEC的计算资源进行了分配。使用粒子群算法为基础算法，改进了粒子编码方式，加入了惩罚函数，和提出粒子修正算法对约束条件进行处理。通过实验仿真，与其它算法相对比，本文所提算法能有效降低系统总成本。同时需要指出的是，本文只考虑了一个RSU下卸载的情况，下一步工作，将考虑多个RSU的协同卸载问题。