双列调心凹面滚子轴承接触载荷分析

杨虎，江岩，张文虎，谢鹏飞，李峰

(1.洛阳轴承研究所有限公司，河南 洛阳 471039；2.河南省高性能轴承技术重点实验室，河南 洛阳 471039； 3.高性能轴承数字化设计国家国际科技合作基地，河南 洛阳 471039；4.北京航天动力研究所，北京 100176； 5.河南科技大学 机电工程学院，河南 洛阳 471003； 6.常州光洋轴承股份有限公司 博士后工作站，江苏 常州 213001)

双列调心凹面滚子轴承结构紧凑，具有良好的调心性能，可以承受一定的倾覆力矩[1-2]，广泛应用于飞机的襟翼、缝翼、方向舵、升降舵等系统。双列调心凹面滚子轴承滚子与滚道之间的接触载荷直接影响轴承的使用寿命和可靠性，以及飞机运行的平稳性。国内外对双列调心凹面滚子轴承的接触载荷研究很多：文献[3]考虑滚子倾斜的影响，假设接触区域压力成线性分布，计算出单列调心凹面滚子轴承滚子与滚道的接触应力；文献[4]提出满装双列调心凹面滚子轴承滚子与滚子、滚子与滚道的接触部位不同，从而大大提高了轴承承载能力；文献[5-8]基于静力学分析了双列调心凹面滚子轴承滚子修形对滚子与滚道间接触应力的影响，并得到了沿滚子长度方向的应力分布；文献[9]通过数值计算和有限元分析得到了单列凹面滚子轴承的承载能力，并对计算结果进行验证。

上述文献对双列调心凹面滚子轴承接触载荷做了大量研究，但未涉及接触载荷特性的动力学研究。鉴于此，建立双列调心凹面滚子轴承动力学分析模型，分析结构参数和工况条件对双列调心凹面滚子轴承接触载荷的影响。

1 双列调心凹面滚子轴承动力学模型

机翼部分示意图如图1所示，后缘襟翼通过2套双列调心凹面滚子轴承绕着机翼的固定部分转动，可以扩大机翼的面积和弯度，达到增加升力和控制阻力的目的，在飞机的起飞、高速飞行以及着陆阶段均起重要作用。双列调心凹面滚子轴承作为机翼的固定部分与后缘襟翼的连接部件，其性能将直接影响飞机的性能。

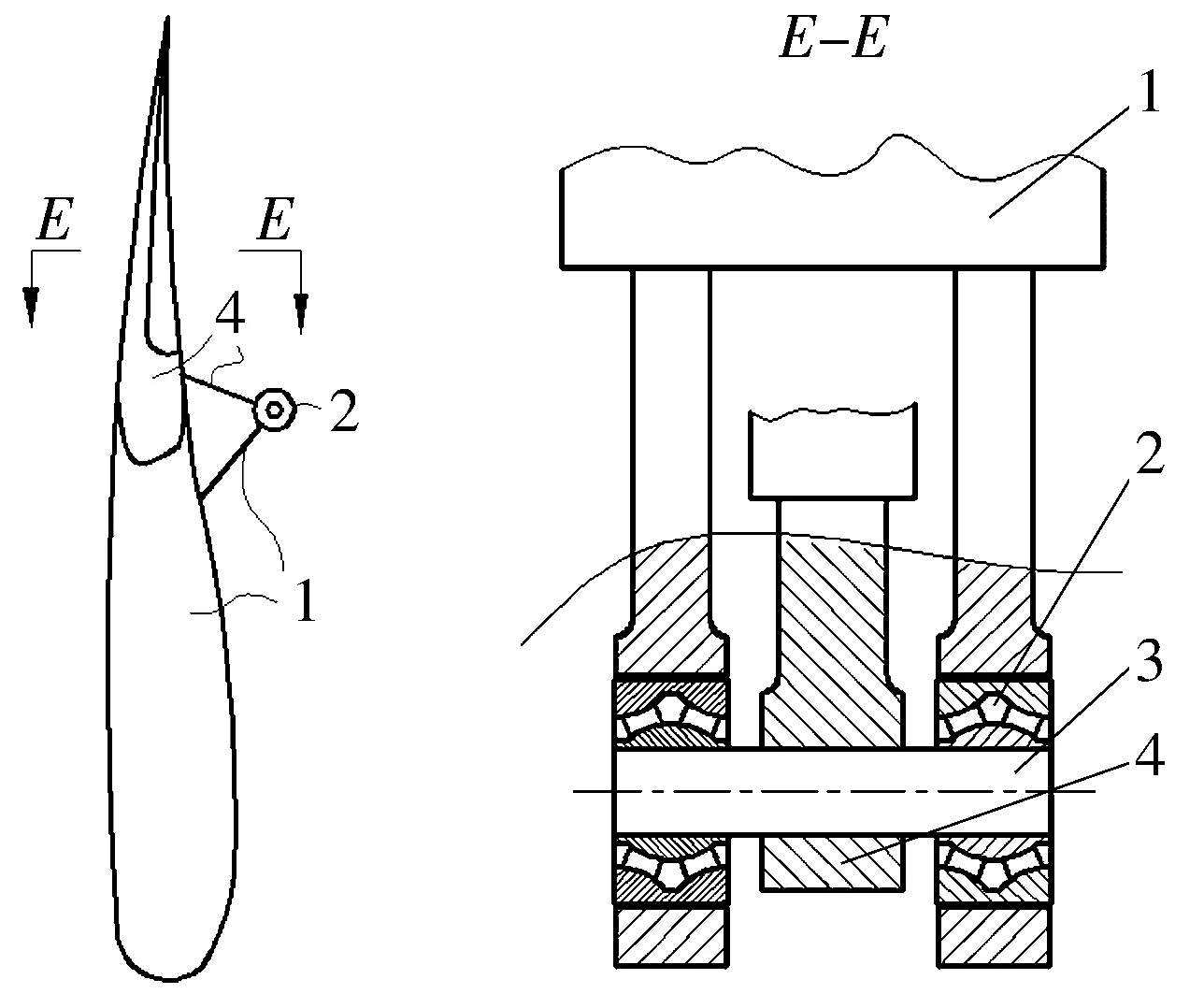
1—机翼固定部分；2—双列调心凹面滚子轴承；3—轴承与后缘襟翼连接件；4—后缘襟翼部分图1 机翼部分示意图Fig.1 Diagram of wing part

1.1 坐标系建立

为便于对双列调心凹面滚子轴承的性能进行分析，建立坐标系(图2)：1)以轴承中心O为原点建立固定坐标系Oxyz，x轴沿轴承轴向方向。2)以滚子中心Ow为原点建立滚子坐标系Owxwywzw，xw轴沿滚子轴线方向，yw轴指向轴承中心。滚子坐标系为动坐标系，随滚子运动。在坐标系Owxwywzw中可以测量滚子自转速度。3)分别以保持架质心Oc1，Oc2为原点建立坐标系Oc1xc1yc1zc1和Oc2xc2yc2zc2，xc1,xc2轴均沿轴承轴向方向。4)以保持架兜孔中心Op为原点建立坐标系Opxpypzp，xp轴沿滚子轴线方向，坐标系随保持架运动，在该坐标系中可以测量滚子相对于保持架兜孔中心的位移。

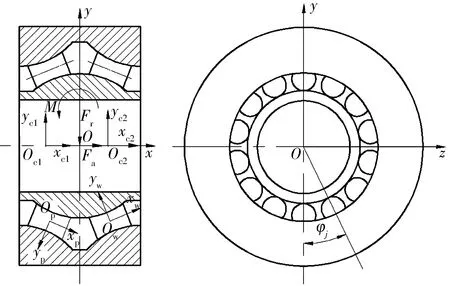
图2 双列调心凹面滚子轴承坐标系Fig.2 Coordinate system of double row spherical concave roller bearing

1.2 动力学微分方程组

滚子受力如图3所示，图中：下标i,e分别代表内、外圈滚道，下标j代表第j个滚子,Qij,Qej分别为内、外圈滚道与滚子之间的法向接触力，Tij,Tej分别为内、外圈滚道与滚子之间的油膜拖动力，MQij,MQej分别为内、外圈滚道与滚子之间的法向接触力所产生的力矩，MTij,MTej分别为内、外圈滚道与滚子之间油膜拖动力产生的力矩，Qcj,Fcj分别为保持架横梁与滚子之间的法向接触力与切向摩擦力，Fwj为滚子离心力。滚子动力学微分方程为

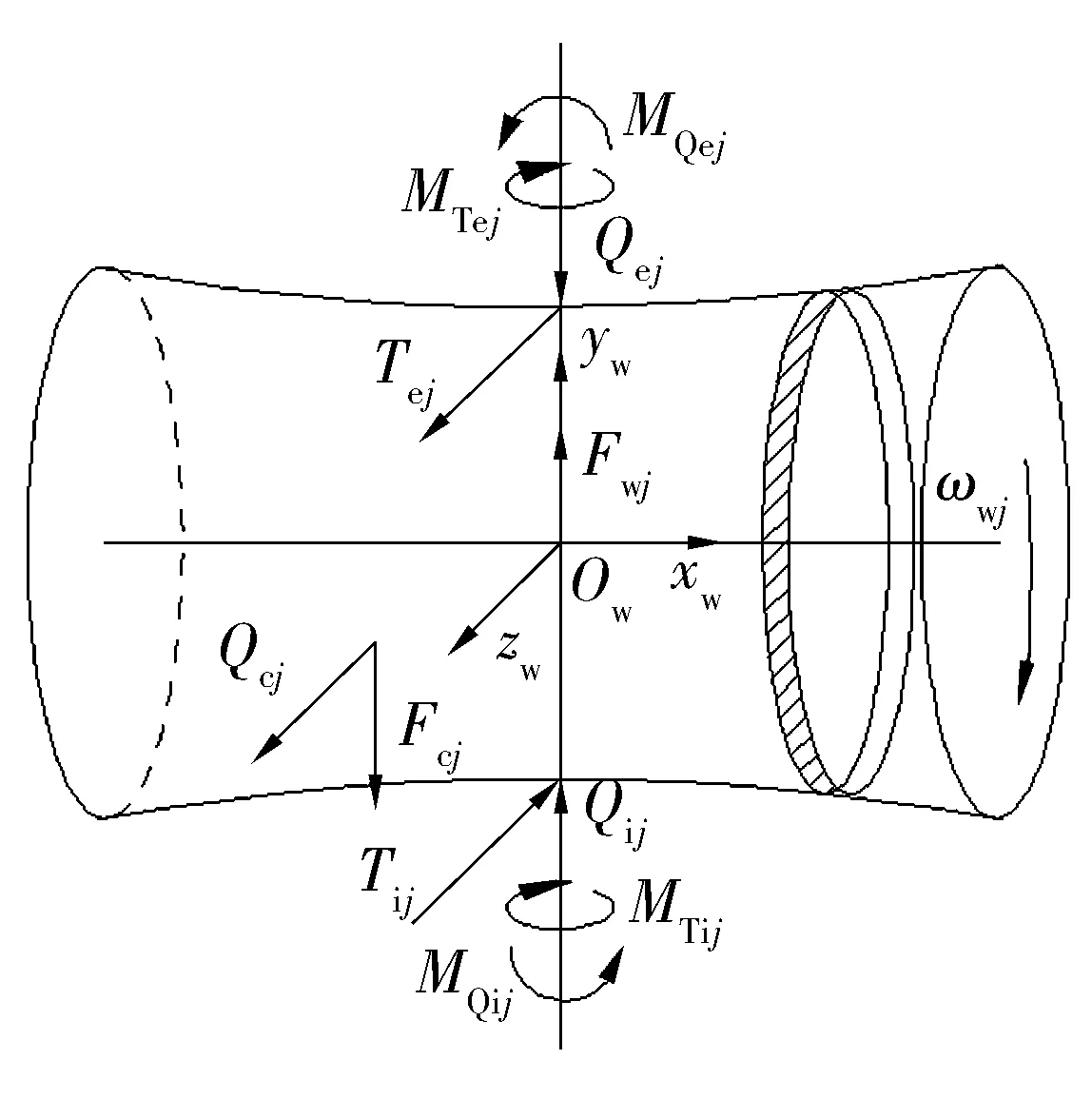
图3 滚子受力示意图Fig.3 Diagram of roller forces

(1)

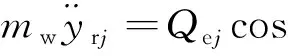
Tejsinφj-Tijsinφj+Qcjsinφj+Fcjcosφj-

Frjcosαecosφj，

(2)

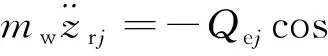
Tejcosφj-Tijcosφj+Qijcosφj+Fcjsinφj-

Fwjcosαesinφj，

(3)

MFejsinαe，

(4)

MQijsinφj∓MTijsinαisinφj±MQcjcosαecosφj∓

MTcjsinαesinφj，

(5)

MQijcosφj±MTijsinαisinφj∓MQcjcosφj±

MTcjsinαesinφj，

(6)

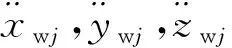
保持架受力如图4所示，图中：Fcy1,Fcy2为内圈对保持架引导力Fc沿法向的分量，Fcz1,Fcz2为内圈对保持架引导力Fc沿切向的分量。保持架动力学微分方程组为

图4 保持架受力示意图Fig.4 Diagram of cage forces

(7)

(Fcz1+Fcz2)sinφj-(Fcy1+Fcy2)sinφj]，

(8)

(Fcz1+Fcz2)sinφj+(Fcy1+Fcy2)sinφj]，

(9)

(10)

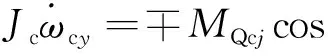
Fcy1cosφj(Bcage-Bc1)-Fcz1sinφj(Bcage-Bc1)+

Fcy2cosφjBc1+Fcz2sinφjBc1，

(11)

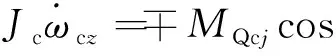
Fcy2sinφjBc1+Fcz2cosφjBc1，

(12)

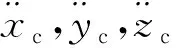
内圈除受轴向载荷、径向载荷和倾覆力矩外，还受到滚子的法向接触力和油膜拖动力的作用，内圈动力学微分方程组为

(13)

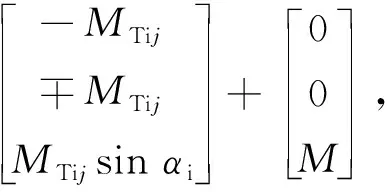
(14)

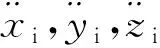
1.3 求解过程

双列调心凹面滚子轴承的运动情况及内部的相互作用复杂，包括滚子与内外圈的作用力、滚子与保持架的作用力及保持架与引导套圈的作用力等，各零件间相互作用力的计算方法参考文献[10]，轴承运动状态及作用力在运动过程中时刻变化，油膜拖动力也时刻变化。

建立双列调心凹面滚子轴承的三维模型，考虑轴承运动过程中拖动力的变化及滚子的倾斜和歪斜等，对所建立的双列调心凹面滚子轴承动力学微分方程进行求解，求解过程如图5所示。

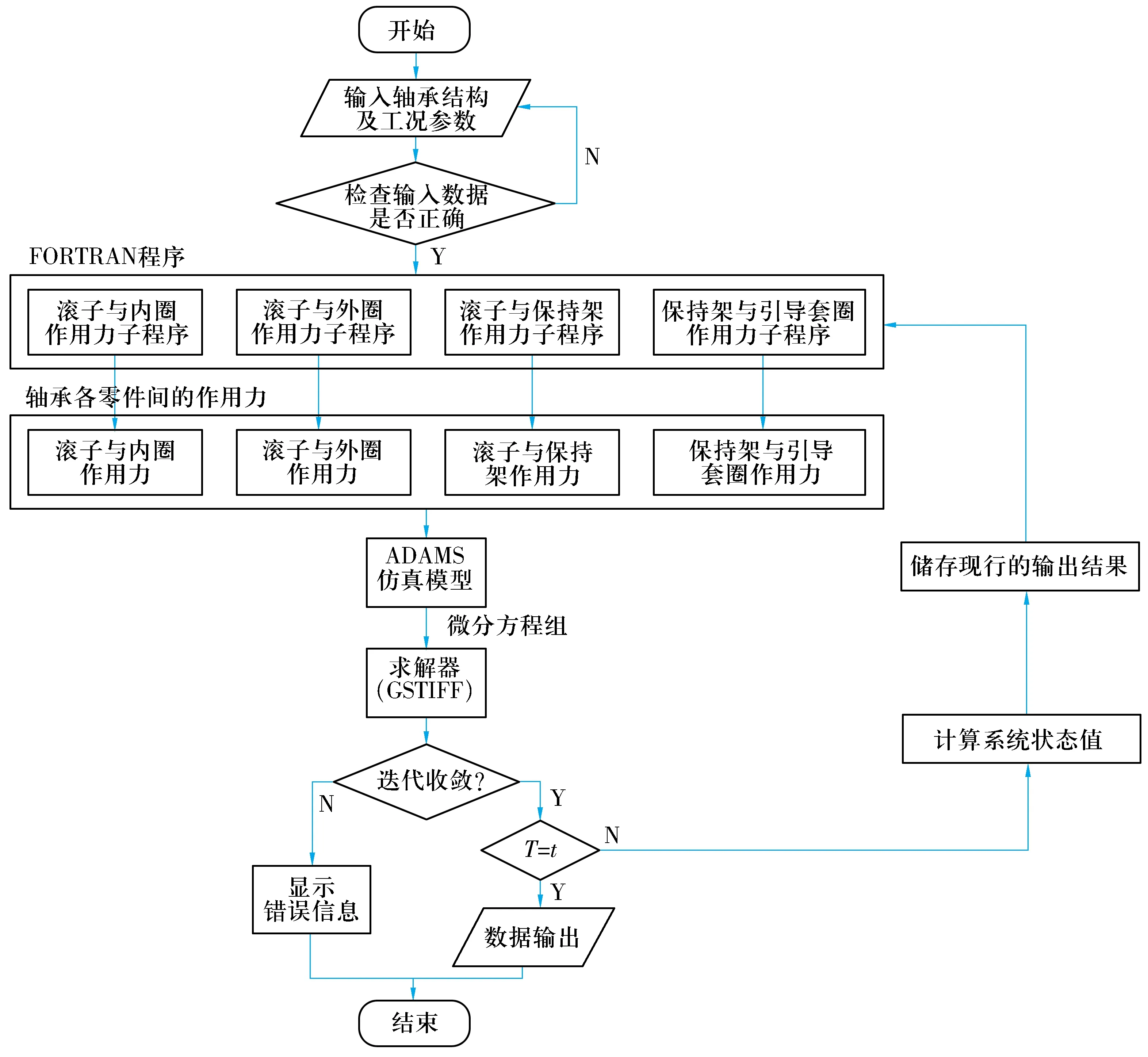
图5 双列调心凹面滚子轴承动力学模型的求解过程Fig.5 Solution process of double row spherical concave roller bearing dynamic model

2 双列调心凹面滚子轴承接触载荷分析

以某双列调心凹面滚子轴承为例进行分析，其主要结构参数见表1。

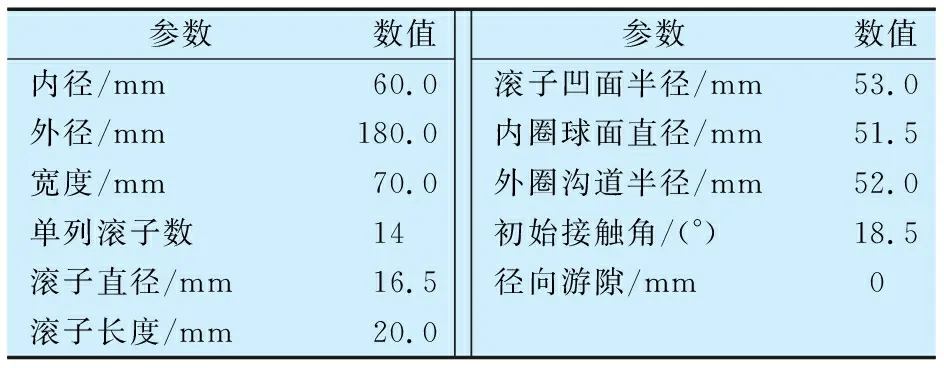
表1 双列调心凹面滚子轴承主要结构参数Tab.1 Main structural parameters of double row spherical concave roller bearing

2.1 模型验证

假设双列调心凹面滚子轴承仅受径向载荷，在不同径向载荷下，本文方法与文献[10]中所采用的静力学分析方法计算的0°方位角处滚子最大接触载荷如图6所示，滚子最大接触载荷随径向载荷增大而增大，2种计算方法一致性较好，验证了本文动力学模型的正确性。本文计算结果较大，这是因为动力学计算中考虑滚子离心力的作用。

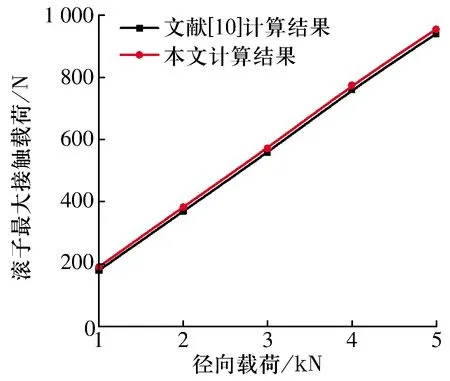
图6 不同径向载荷下滚子最大接触载荷Fig.6 Maximum contact load of rollers under different radial loads

2.2 工况参数对滚子最大接触载荷的影响

2.2.1 轴向载荷

在转速(飞机机翼摆动过程中的最大转速)为1 000 r/min，径向载荷为1 000 N，不受倾覆力矩时，轴向载荷对双列调心凹面滚子轴承滚子最大接触载荷的影响如图7所示，由图可知：1)随轴向载荷增大，左列滚子最大接触载荷减小，右列滚子最大接触载荷增大，这是由于向右的轴向载荷增大会使左列滚子受载减小，右列滚子受载增大。2)当轴向载荷与径向载荷的比值达到6.35/10时，左列滚子最大接触载荷突然下降，而右列滚子突然上升，这是由于此时左列滚子不受力，所有外部作用力均由右列滚子承受。

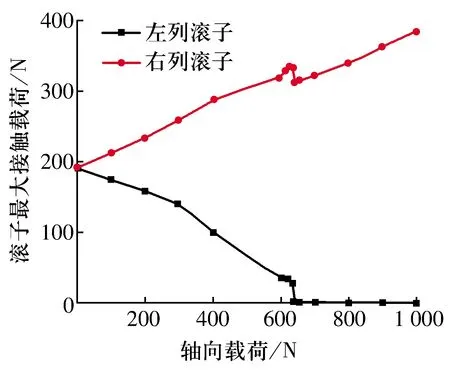
图7 轴向载荷对滚子最大接触载荷的影响Fig.7 Influence of axial load on maximum contact load of rollers

2.2.2 径向载荷

在转速为1 000 r/min，仅受径向载荷时，径向载荷对双列调心凹面滚子轴承滚子最大接触载荷的影响如图8所示，随径向载荷增大，滚子最大接触载荷增大。

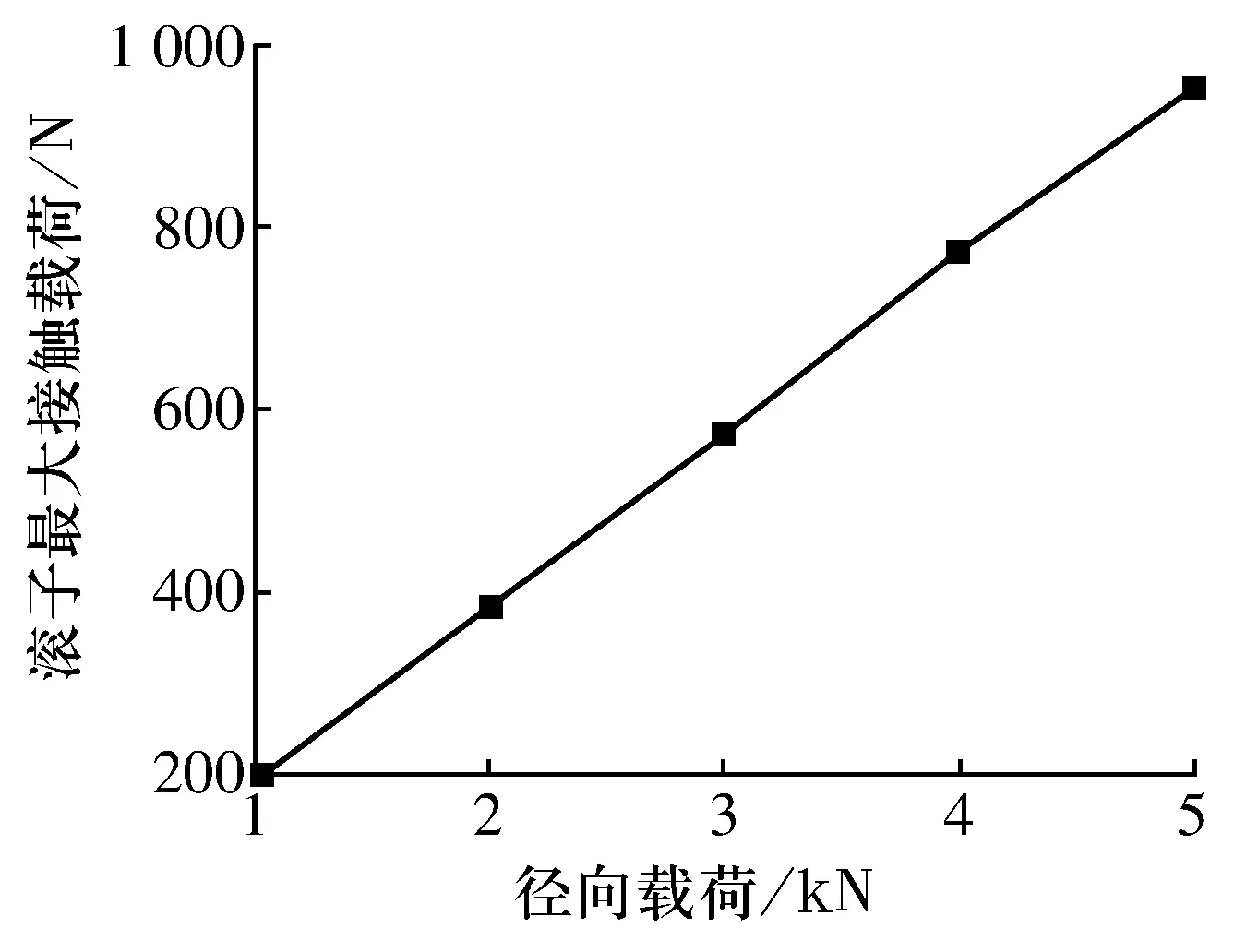
图8 径向载荷对滚子最大接触载荷的影响Fig.8 Influence of radial load on maximum contact load of rollers

2.2.3 倾覆力矩

在转速为1 000 r/min，径向载荷为1 000 N，不受轴向载荷时，倾覆力矩对双列调心凹面滚子轴承滚子最大接触载荷的影响如图9所示，随倾覆力矩增大，左右列滚子接触载荷变化均在1 N之内，这是由于内圈为球面，当受到倾覆力矩时，内圈与滚子之间的接触特性几乎不发生变化。

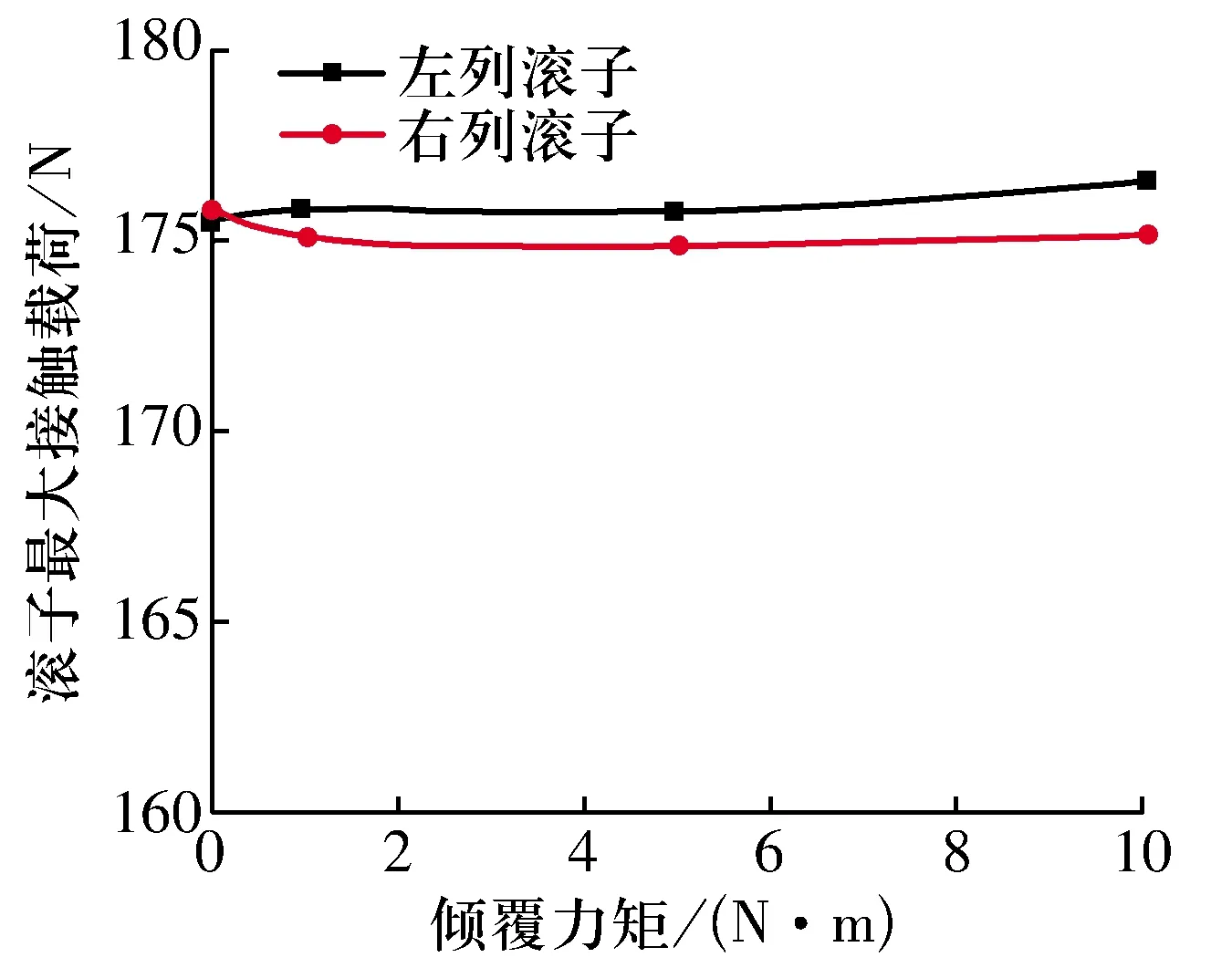
图9 倾覆力矩对滚子最大接触载荷的影响Fig.9 Influence of overturning moment on maximum contact load of rollers

2.2.4 转速

在轴承仅受1 000 N径向载荷时，转速对双列调心凹面滚子轴承最大接触载荷的影响如图10所示，随转速增大，滚子最大接触载荷呈增大趋势。这是因为转速主要影响双列调心凹面滚子轴承滚子所受的离心力，在外载荷不变的条件下，转速越大，滚子所受离心力越大，滚子背离轴承轴线向外运动的趋势越明显，滚子最大接触载荷增大。

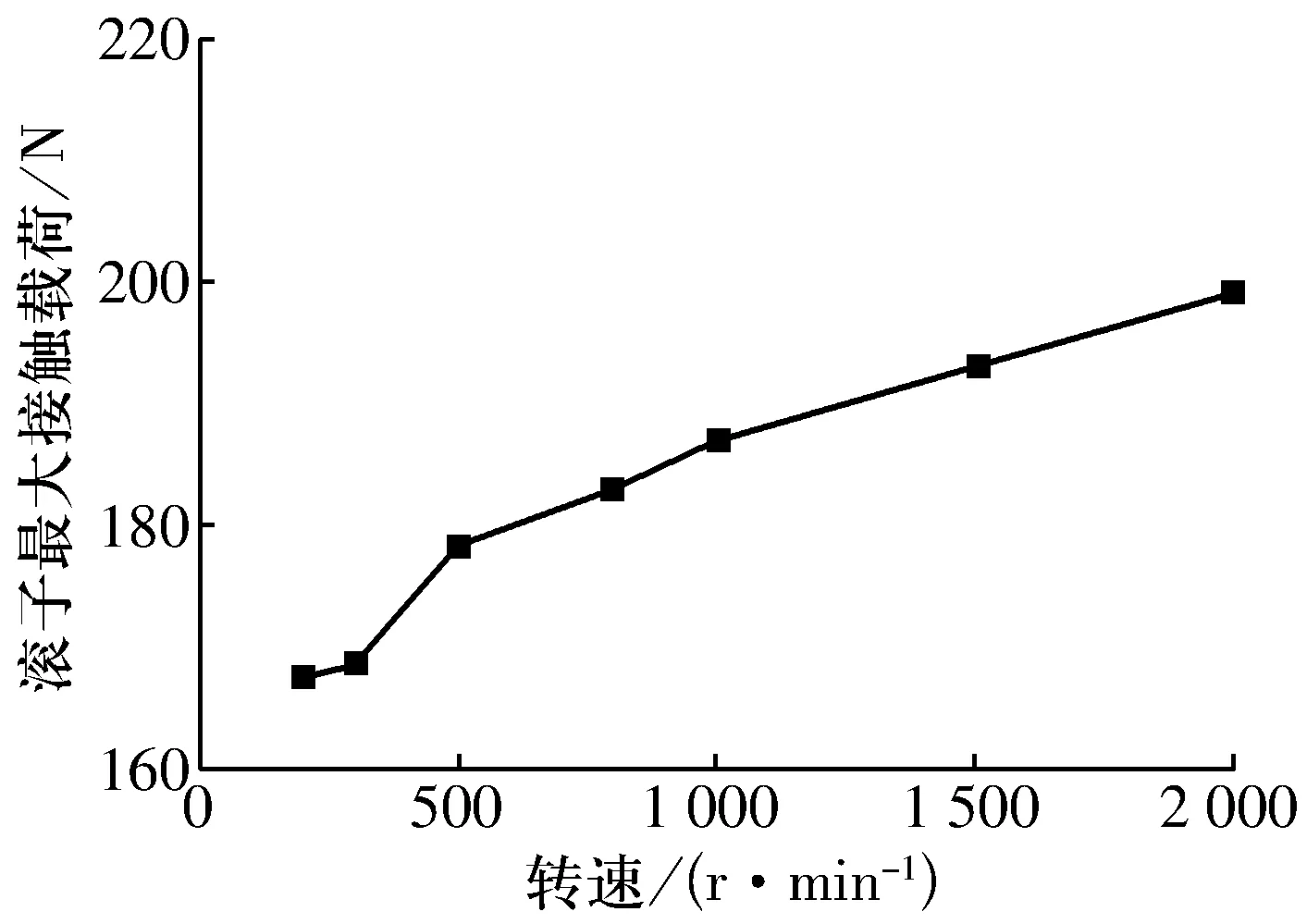
图10 转速对滚子最大接触载荷的影响Fig.10 Influence of speed on maximum contact load of rollers

2.3 结构参数对滚子最大接触载荷的影响

分析结构参数对滚子最大接触载荷的影响时，轴承转速取1 000 r/min,径向载荷取1 000 N，不承受轴向载荷和倾覆力矩。

2.3.1 滚子数

在滚子长度为20 mm，径向游隙为0时，滚子数对双列调心凹面滚子轴承滚子最大接触载荷的影响如图11所示，随滚子数增多，滚子最大接触载荷减小。这是由于在外载荷不变的条件下，轴承受载区域不变，受载区内的滚子数增加，滚子接触载荷减小。在满足保持架强度要求的前提下，可适当增加滚子数。

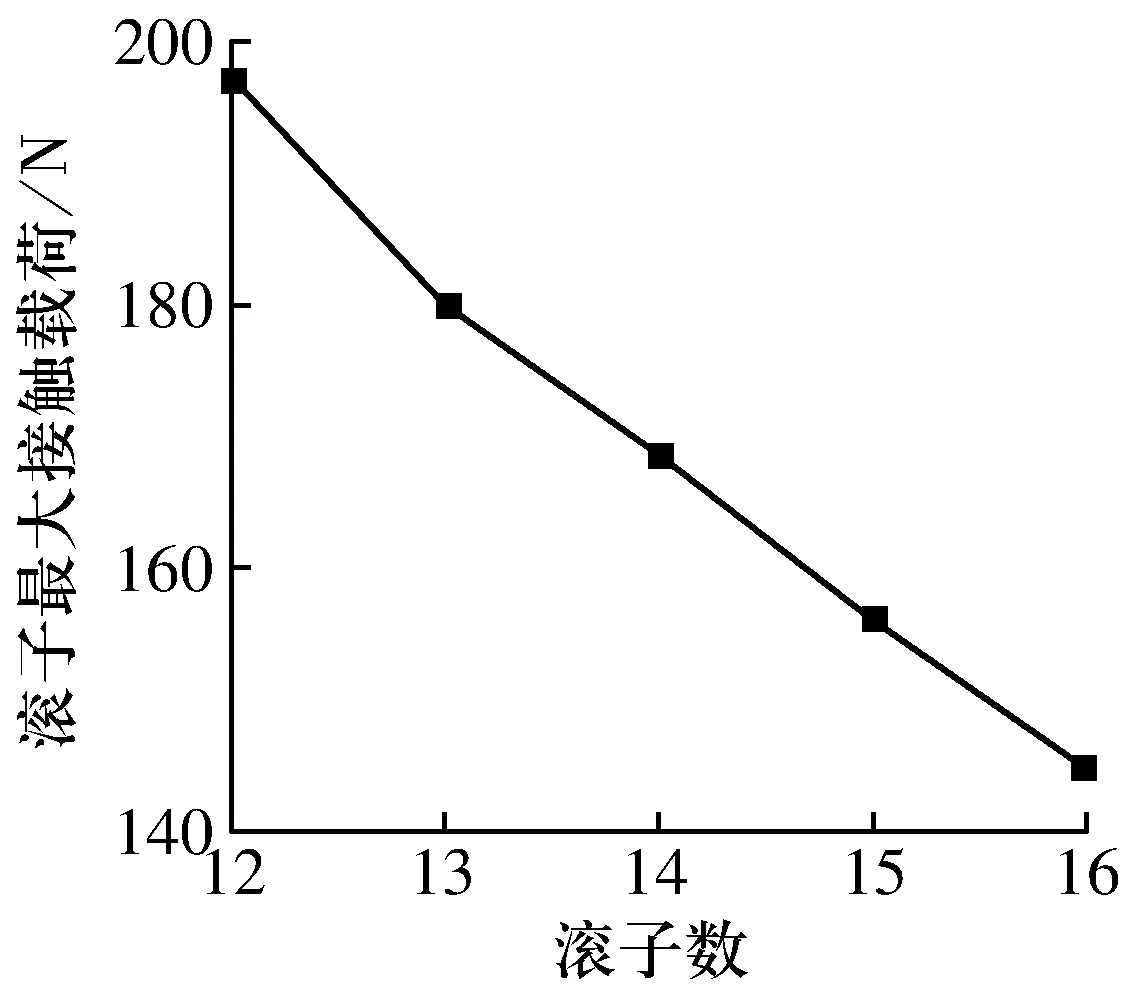
图11 滚子数对滚子最大接触载荷的影响Fig.11 Influence of number of rollers on maximum contact load of rollers

2.3.2 滚子长度

在滚子数为14，径向游隙为0时，滚子长度对双列调心凹面滚子轴承滚子最大载荷的影响如图12所示，随滚子长度增加，滚子最大载荷减小。这是由于滚子越长，滚子与滚道的接触区域越大，在相同外载荷下承受载荷越小。

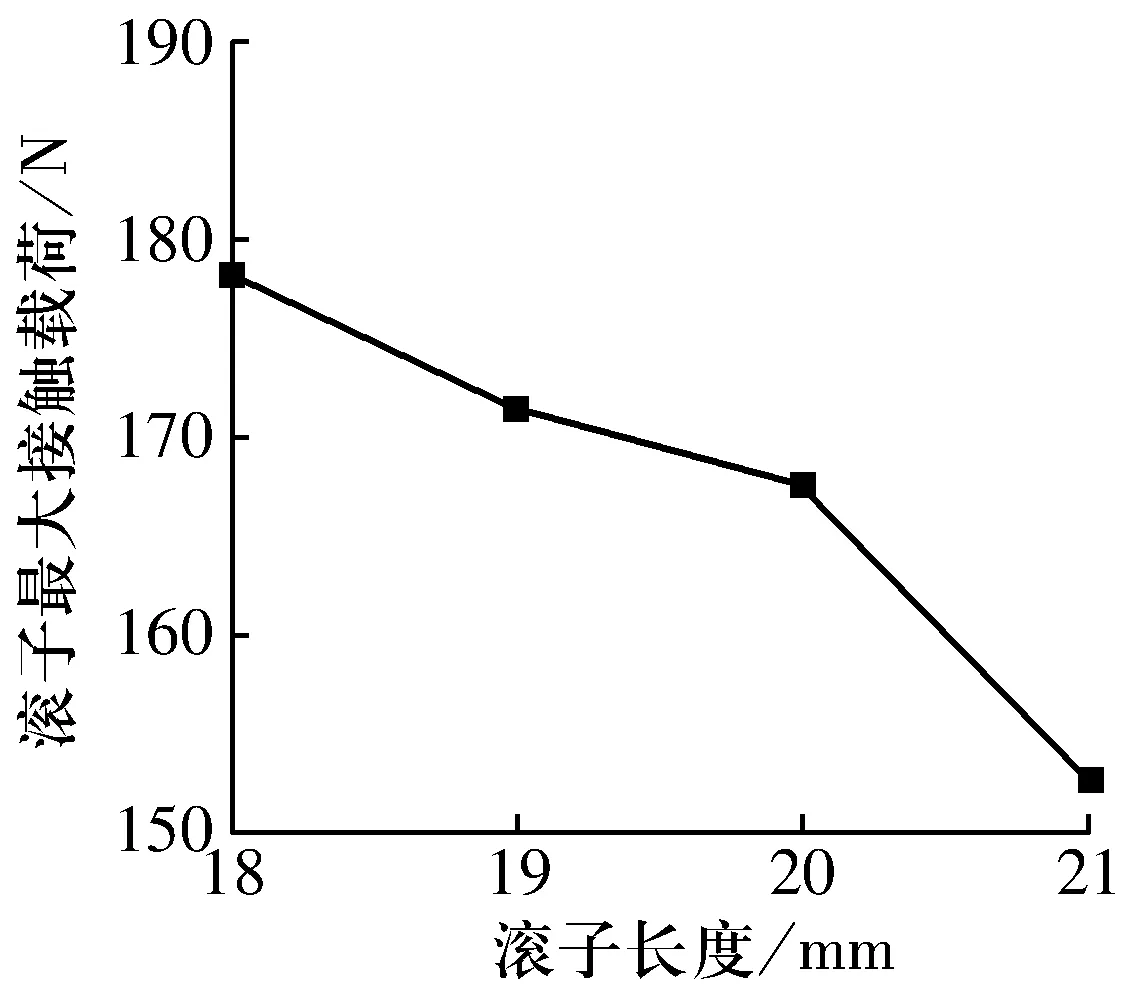
图12 滚子长度对滚子最大接触载荷的影响Fig.12 Influence of length of rollers on maximum contact load of rollers

2.3.3 径向游隙

在滚子长度为20 mm，滚子数为14时，径向游隙对双列调心凹面滚子轴承滚子最大接触载荷的影响如图13所示，随径向游隙增大，滚子最大接触载荷呈先减小后增大的趋势。这是由于径向游隙减小会导致受载滚子数增加，使滚子最大接触载荷减小，但当径向游隙为-0.001 mm时，所有滚子均承载，游隙继续减小会使每个滚子的接触载荷均增大。

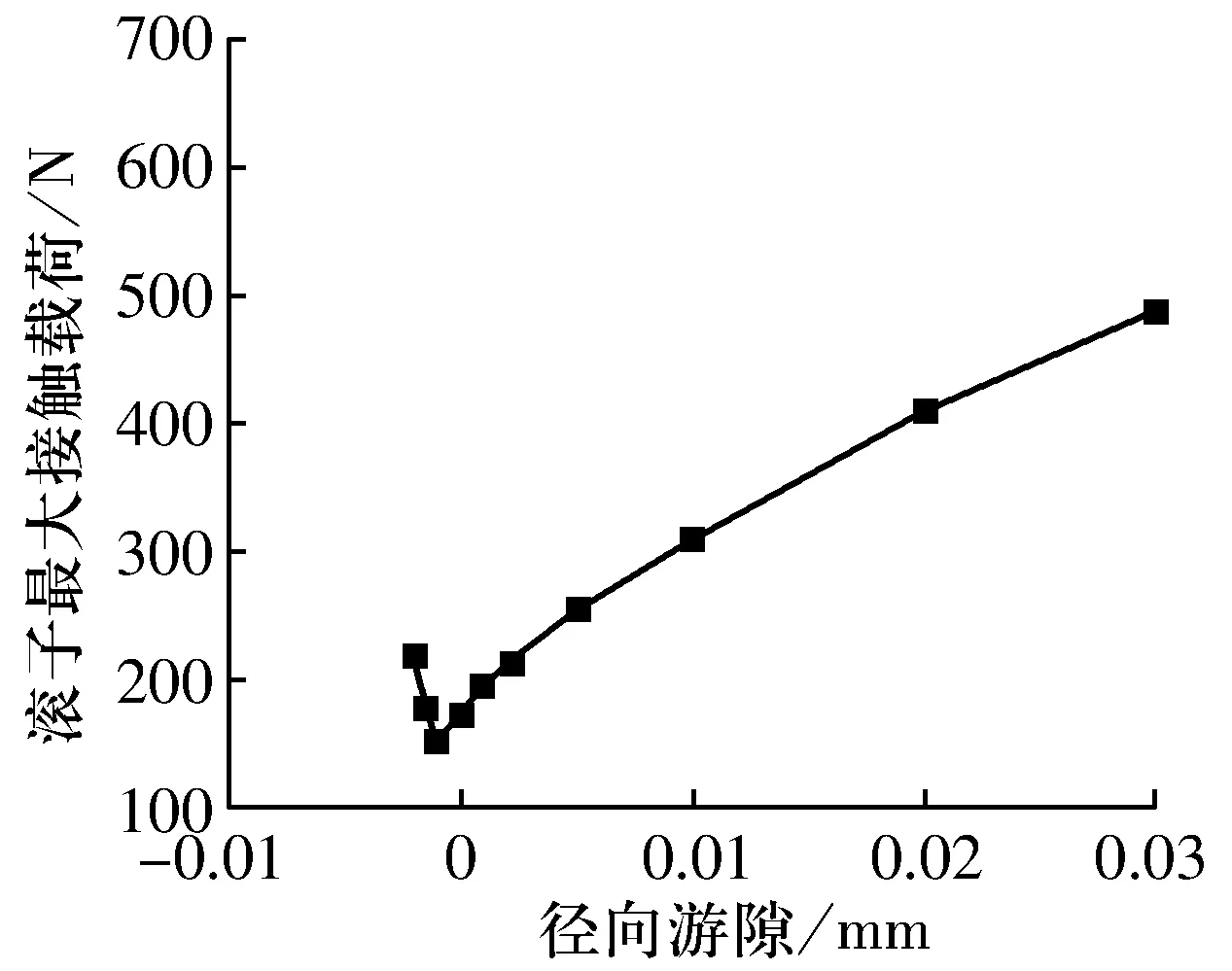
图13 径向游隙对滚子最大接触载荷的影响Fig.13 Influence of radial clearance on maximum contact load of rollers

3 结论

在文中设定的条件下，分析得到双列调心凹面滚子轴承接触载荷具有以下特性：

1)随轴向载荷增大，左列受载滚子数减少，右列受载滚子数增加。随径向载荷增大，滚子最大接触载荷增大。当轴向载荷与径向载荷的比值达到6.35/10时，左列滚子不受力，所有外部作用力均由右列滚子承受。随倾覆力矩增大，左右列滚子最大接触载荷几乎不变。

2)随转速增大，滚子最大接触载荷呈增加趋势。

3)随滚子数增多，滚子最大接触载荷减小。随滚子长度增加，滚子最大接触载荷呈减小趋势。

4)随径向游隙减小，受载滚子数增加，滚子最大接触载荷减小，当径向游隙为-0.001 mm时，所有滚子均承载，径向游隙继续减小会使滚子最大接触载荷增大。