第三代轮毂轴承负游隙的弹性变形检测方法

田助新，李江全，葛志华

(1.华中科技大学 机械科学与工程学院，武汉 430074；2.湖北新火炬科技有限公司，湖北 襄阳 441004；3.湖北文理学院 机械工程学院，湖北 襄阳 441053)

轮毂轴承是汽车的关键功能部件，其运行状态直接决定了整车的安全性、舒适性和可靠性[1-2]。目前，市场上的轿车多采用第三代轮毂轴承，与前两代轮毂轴承相比，第三代轮毂轴承的集成度更高，有利于汽车的轻量化设计。为降低滚动轴承在高速转动时的打滑率[3]，通常会在第三代轮毂轴承装配完成后施加一定的预紧，形成负游隙。

轮毂轴承负游隙本质上是钢球在预紧力作用下发生的弹性变形，负游隙过大，会使轴承转动中产生很大的摩擦力矩和接触应力，严重时会直接导致轴承失效；负游隙过小，则起不到预紧效果。由于钢球封装在轴承内部，其变形量难以直接测量。文献[2]将轮毂轴承等效为非线性弹簧质量系统，通过测量轴承接触副的固有频率间接得到轴承负游隙。文献[4]基于多体动力学提出了一种光线追踪算法，利用轮毂轴承内圈的运动表征负游隙。文献[5]建立了轮毂轴承预紧力与负游隙之间的关系，并提出了通过测量轴承预紧力来计算负游隙的方法。文献[6]通过测量轮毂轴承外圈与钢球接触副对超声波的反射信号来估算轴承预紧力，为轴承预紧力的测量提供了一种新思路。

在上述研究的基础上，基于赫兹接触理论建立轴承负游隙与弹性变形量差值之间的映射关系，可将负游隙的测量转换成弹性变形量差值的测量，并在此基础上提出一种快速、简便测量轮毂轴承负游隙的方法。

1 测量方法

通过理论计算得到负游隙δ与弹性变形量差值(A0-Ac)之间的对应关系，将负游隙的测量转换成弹性变形量差值的测量。

轮毂轴承负游隙的弹性变形检测如图1所示，具体步骤如下：

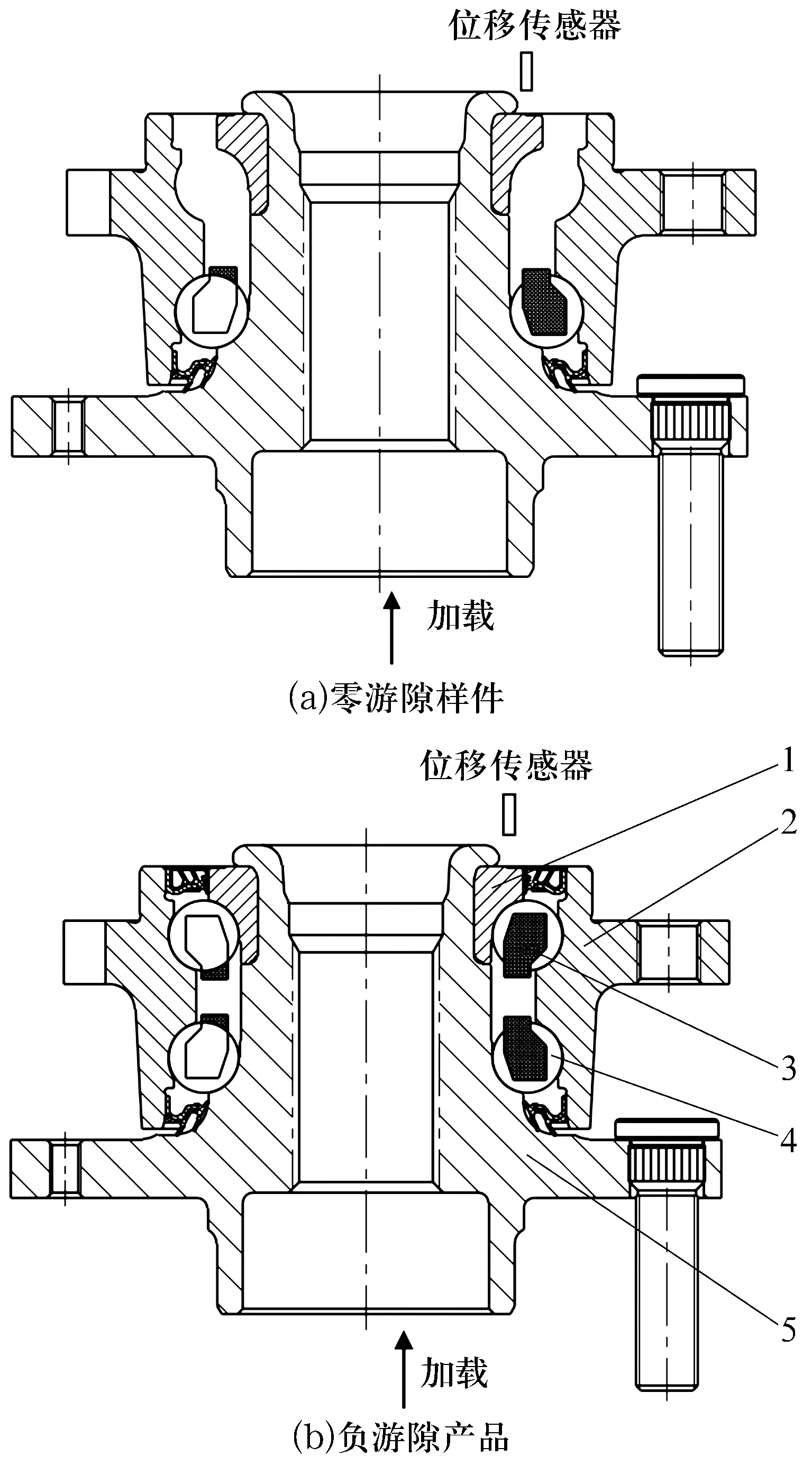
1—内圈；2—外凸缘；3—上列钢球保持架组件；4—下列钢球保持架组件；5—内凸缘图1 刚性测量法示意图Fig.1 Diagram of rigidity measurement method

1)制作零游隙样件，即一件无上列钢球的产品。固定外凸缘，使传感器与内圈端面接触，监控刚性位移量。

2)轴向线性增大载荷至F1，旋转内凸缘并记录轴向位移A01；再线性减小至载荷F2，旋转内凸缘并记录轴向位移A02；(A01-A02)即为零游隙样件的弹性变形量，记为A0，其为该产品变形量的极大状态。

3)将测试件换成正常的负游隙产品，重复上述操作，得到正常产品的弹性变形量Ac。

4)测得弹性变形量差值(A0-Ac)后，根据负游隙与弹性变形量差值之间的对应关系即可得到轮毂轴承负游隙。

2 分析过程

在轴承加载过程中，钢球接触角会发生轻微的变化，但实际应用中接触角变化引起的结果误差不超过3%，因此，为简化中间分析过程，本研究未考虑加载过程中接触角的变化。

轴向加载F时，每个钢球的受力Qz为[7]

(1)

式中：Z为单列钢球个数；α为接触角。

此时，钢球的轴向变形量δz为

(2)

式中：δ*为点接触椭圆积分参数；∑ρ为与钢球接触零件的曲率函数；E*为轴承材料泊松比和弹性模量的综合参数。以上变量均由轴承结构参数确定，对于给定结构的轮毂轴承，这几个变量均为常数。

2.1 零游隙样件分析

当施加外载荷F1时，零游隙样件中钢球的总变形为

(3)

式中：∑ρ内，∑ρ外分别为与钢球接触的内、外圈的曲率函数。

此时，可以通过测量得到轮毂轴承端面的位移变化量，即轮毂轴承的总变形为A01，两者之间存在如下关系

Am01=A01-Ab01,

(4)

式中：Ab01为除钢球变形之外轮毂轴承其他零件的变形量。

当施加外载荷F2时，零游隙样件钢球的总变形为

(5)

在加载F2时测量轮毂轴承端面位移变化量，即轮毂轴承的总变形为A02，除钢球变形之外轮毂轴承其他零件的变形量为Ab02，则

Am02=A02-Ab02。

(6)

因此，零游隙样件的弹性变形量A0为

A0=A01-A02=(Am01+Ab01)-(Am02+Ab02)。

(7)

2.2 负游隙产品分析

轮毂轴承初始负游隙为δ，在未施加载荷前，上、下列钢球的变形均为δ/2。当施加不足以将上列钢球完全顶松的外力F1后，上、下列钢球的受力分别为F02，F01。此时，上、下列钢球的二次变形量分别为

(8)

(9)

在上列钢球没有完全卸载时，下列钢球被压紧多少，上列钢球就会放松多少，即

Amc1=Amc2。

(10)

联立(8)—(10)式可得

(11)

当轴承承受来自下方的载荷F1时，力平衡关系为

(12)

由(8)，(11)，(12)式可得

(13)

在加载F1时，测量轮毂轴承端面位移变化量，即轮毂轴承的总变形为Ac1，除了钢球变形之外的轮毂轴承的变形量为Abc1。则钢球的二次变形量Amc1为

Amc1=Ac1-Abc1。

(14)

将(14)式代入(13)式可得

(15)

同理，在施加载荷F2时可得

(16)

对于给定的负游隙δ，可以利用牛顿迭代法求解出Ac1-Abc1和Ac2-Abc2，然后通过多项式拟合得到Ac1-Abc1和Ac2-Abc2与负游隙之间的关系式，即

Ac1-Abc1=f1(δ)，

(17)

Ac2-Abc2=f2(δ)，

(18)

将(17)，(18)式相减，可得负游隙产品的弹性变形量Ac为

Ac=Ac1-Ac2=Abc1-Abc2+f(δ)，

(19)

f(δ)=f1(δ)-f2(δ)。

(20)

2.3 弹性变形量与负游隙之间的关系

由于零游隙样件与负游隙产品之间唯一的区别只是零游隙样件缺少上列钢球，因此，可以认为在相同的载荷作用下，两者除钢球变形之外的轴承变形量是相同的，即

Ab01=Abc1，Ab02=Abc2。

(21)

因此，将(19)与(7)式相减即可得到所求的弹性变形量差值，即

A0-Ac=Am01-Am02-f(δ)。

(22)

3 算例

为更直观的说明本方法在实际生产中的应用过程，以某型第三代轮毂轴承为对象进行分析。该轮毂轴承的结构参数见表1。2次施加的载荷F1，F2分别为20，2 kN(载荷值可以任意选取，但为了更好区分2次加载过程中轴承轴向位移测量值的差异，2次加载力的大小最好相差5倍以上)，计算得到负游隙值δ与弹性变形量差值(Ac-A0)之间的关系如图2所示。对于该型号的任意轴承，只要测量出该轴承的弹性变形量差值(Ac-A0)之后，即可通过该关系图得到对应的负游隙值。

表1 某型号轮毂轴承结构参数Tab.1 Structural parameters of a certain type of hub bearing

图2 轮毂轴承的负游隙与弹性变形量差值之间的关系Fig.2 Relationship between negative clearance and difference in elastic deformation of hub bearing

4 结束语

针对当前第三代轮毂轴承负游隙无法直接测量的难题，基于赫兹接触理论提出了一种刚性测量法。通过引入一个零游隙样件，建立了轮毂轴承负游隙与弹性变形量差值之间的映射关系，在此基础上，将负游隙的测量问题转换成轴承弹性变形量差值的测量。通过本方法的应用，轮毂轴承生产产家可以在产品出厂前进行负游隙的检测，确保出厂的轮毂轴承负游隙处于较优状态，有助于提高出厂轮毂轴承的使用寿命。