保护学生奇思异想 软件助学提高素养——以一个学生“歪想”引出的探究为例

俞 纲 (云南省昆明市第三中学 650599)

“学习起于思考，思考源于问题”，教学中常有一些“特别”的学生提出一些“不合情境”的问题，当这些问题比较偏或者完全不是平时的“教学套路”时，不少教师常以“考试绝对不会这样考查”为由告诫学生放弃歪想．这可能会挫伤学生提问思考的积极性，同时可能会固化学生思维，不利于其探究能力的提升．因此，对于学生的奇思异想，教师应该认真对待，仔细挖掘其中价值，对于有利于学生素质培养的问题，可引导学生进行探究．恰当借助GeoGebra软件强大的代数计算与几何图形处理能力，让学生的探究活动有效开展，有利于促进其核心素养的发展与综合能力的提高．本文从学生对一个问题的“歪想”出发，指导学生借助GeoGebra进行了一次完整探究，从中收获了一些感悟，与大家交流．

1 学生的“歪想”

在一个底面半径为1、高为2的圆锥模具内平放一个圆柱体，则能放下的圆柱的最大体积为多少？

分析 本题是作业中出现的一个中等难度的应用题，考查立体几何知识与导数知识的综合运用．通过作出轴截面，学生得出如下求解思路．

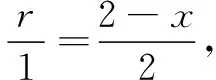
图1

课后有几位思维灵活的学生对题意提出了不同看法，若圆柱横放在圆锥内，该体积是否会更大？题设这样一变，难度陡然增加，显然这并不是出题者的本意，是对题目的误解与“歪想”.用高中知识能否解决？笔者也犹豫了一番，考虑到应该保护学生的积极性，同时这也许正是锻炼学生自主探究能力的好契机，即使该问题可能“超纲”，笔者也决定指导学生对该问题进行探究．由于该问题相对复杂，笔者建议学生使用GeoGebra助力探究．

2 探究的过程

首先通过GeoGebra制作一个动态3D图形(图2).通过观察思考，大家决定将此问题分化为三个小问题逐一研究解决．

图2

问题1设圆锥内接圆柱的高为2m，表示出圆柱上下底所在的平面截圆锥所得的图形并写出方程．

问题2在问题1所表示的平面区域中放置一个面积最大的圆．

问题3以m为自变量，写出圆柱体积V关于m的函数关系式，进而求其最值．

2.1 问题1的研究

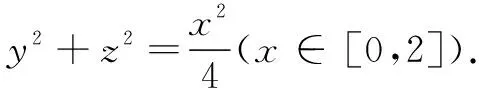
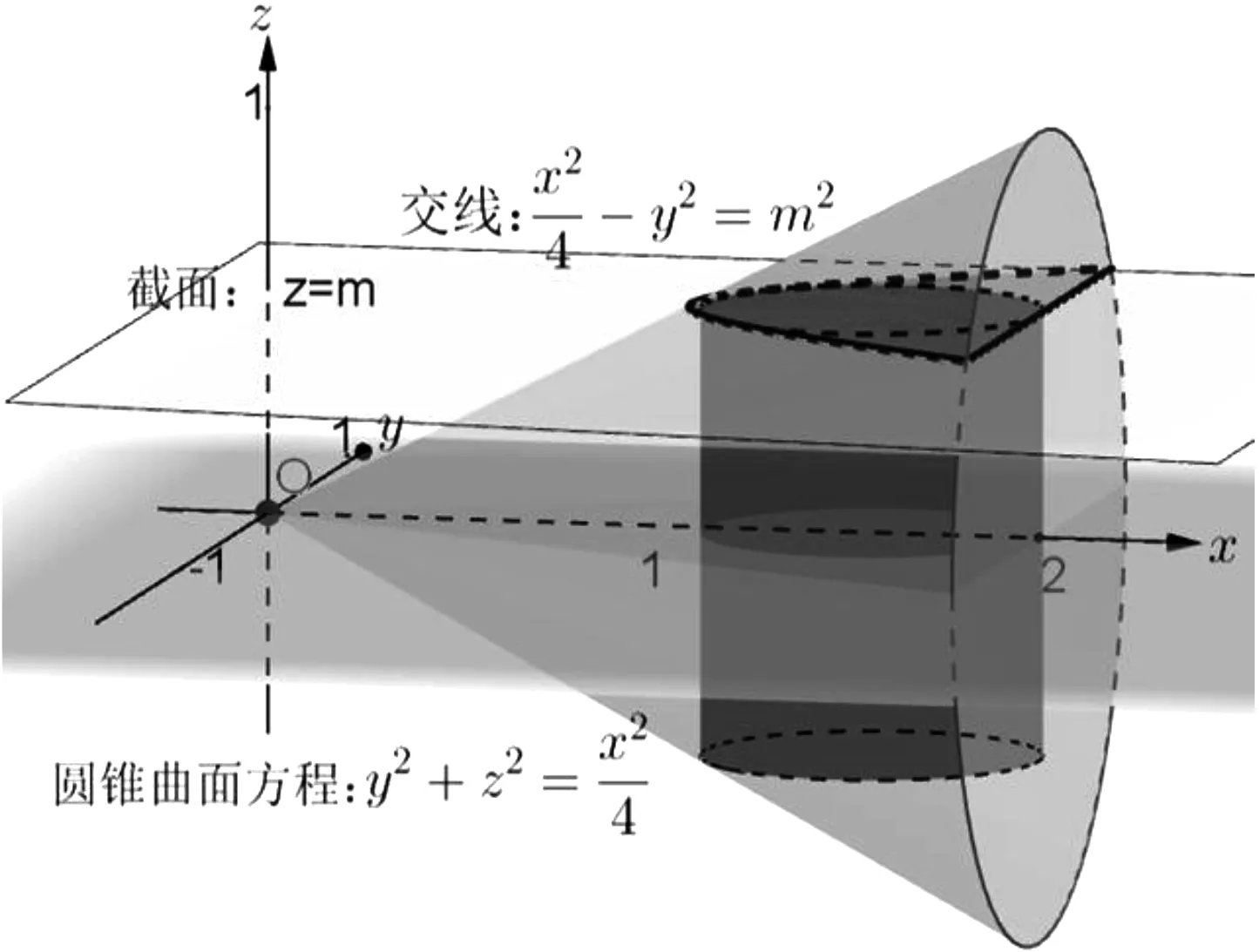
图3

2.2 问题2的研究

在问题1所得到的区域中如何放置面积最大的圆？学生以前没有处理类似问题的经验.笔者指导学生通过GeoGebra作示意图观察，通过把该图形投影到xOy面内研究，学生总结出该圆的性质：与双曲线相切，同时与直线x=2也相切，由图形的对称性可得该圆圆心必定在对称轴x轴上．如何理解圆与双曲线的相切呢？高中教材并没有相应的定义，学生通过讨论提出类比曲线公切线的思想，即以双曲线与圆在同一点处有公共切线的方法来研究，先用代数方法表示出结果，再用GeoGebra来验证这个方法是否正确．

(1)计算圆的半径

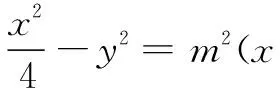
图4

(2)检验发现问题

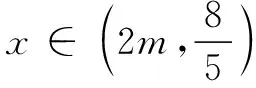
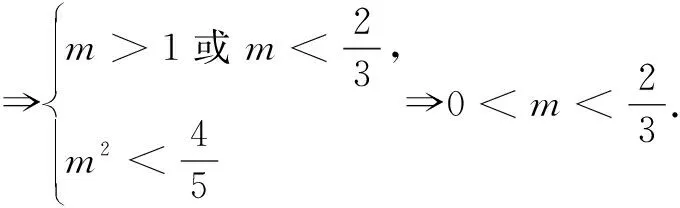
(3)完善方法

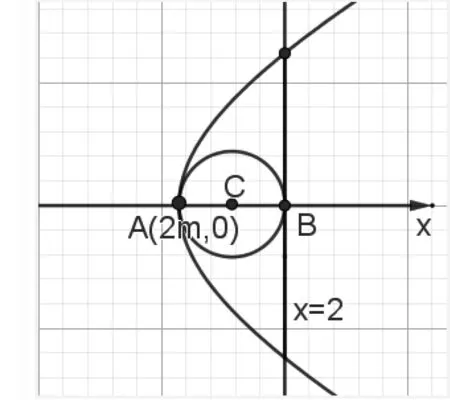
图5

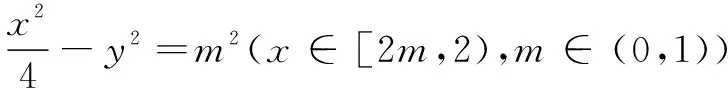
2.3 问题3的研究

基于以上研究，设圆锥内接圆柱的高为2m，其底面圆的半径为r．

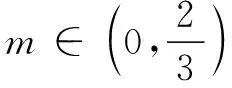
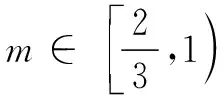
得到计算结果后，学生再次运用GeoGebra绘制出图形，并计算出圆柱体积，发现与所算答案是一致的．

3 探究的优化

重新审视探究过程，笔者提出两点建议让学生再思考．建议一是对于问题2的探究，即双曲线与圆相切的计算，可以不用分类研究，直接运用双曲线上一点到圆心的距离最小值作为该圆半径即可．学生按此思路，对问题2的探究作了如下修改：

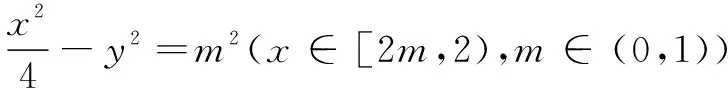
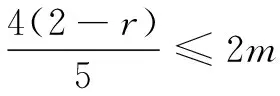
建议二是能否对此问题进行一般性的研究．由于该问题的一般性研究的代数计算过于复杂，学生最终没能完成，但有了此题探究的铺垫，笔者最终带领学生对该问题的一般情况进行了完整探究，由于篇幅原因，这里不再叙述．

4 总结与反思

此次探究使学生经历了质疑问题，提出并分析问题，计算、检验、改进，最终解决问题的完整过程，同时拓展研究出一般性的结论．虽然这个问题本身不是自然建模形成的问题，但学生解决它的过程与《普通高中数学课程标准(2017年版)》所提到数学建模的表现(发现和提出问题，建立和求解模型，检验和完善模型，分析和解决问题)是一致的．若一开始笔者受惯性思维左右，让学生用现有知识理解题意并放弃“歪想”，将错失此次良机；若没有GeoGebra几何图形绘制功能与代数计算功能的帮助，学生也难以深入探究与检验．通过软件的辅助，学生基本在所学知识范畴内解决了这个问题，这极大地激发了其自主探究的兴趣，提升了实践能力，增强了类比猜想意识和科学精神，对他们而言确实是一次完整且有益的探究体验．在着力培养学生核心素养的背景下，作为一线教师，我们一方面应该增强自身的数学知识与信息技术处理能力，另一方面要睁开“慧眼”，重视学生的各种问题，并擅于从中寻找适合学情的探究问题以引导学生探究，促进其探究能力的提升与核心素养的发展．