问题教学的实践与认知——以“一次函数的图象和性质”复习课为例

吴明威 (江苏省苏州市吴中区木渎南行中学 215101)

《义务教育数学课程标准(2011年版)》提出：初步学会从数学的角度发现问题和提出问题，综合运用数学知识解决简单的实际问题，增强应用意识，提高实践能力．[1]笔者在教学听课活动中，经常看到的情境是教师抛出一系列题目，学生逐个分析解决，忙得不亦乐乎，看似热闹，学生的能力却无从得以提升．能在课堂中围绕题目条件，让学生发现和提出问题，则会使学生的数学学习走向深入．北京师范大学资深教授、中国教育学会名誉会长顾明远讲到：学生是教育的主体，是主动的发现者、探索者，这个思想值得我们去探索其实践途径．

笔者近期在一次中考复习交流中，展示了一节“一次函数的图象和性质”的复习课，基于培养学生发现和提出问题的能力，笔者对整节课的设计以一道2020年南通市数学中考题为论题，围绕一次函数知识点对题目条件进行层层改编，鼓励学生大胆提出与之相关的大量数学问题．下文谈谈自己对这次例题改编和问题引领的构思和看法．

原题(2020年南通市第21题)如图1，直线l1：y=x+3与过点A(3，0)的直线l2交于点C(1，m)，与x轴交于点B．

(1)求直线l2的解析式；

(2)点M在直线l1上，MN∥y轴，交直线l2于点N，若MN=AB，求点M的坐标．

1 立足原题条件 自主提出问题

爱因斯坦曾说过：提出一个问题比解决一个问题更重要．我们平时解决问题比较多，而提出问题很少，这里，笔者给学生提出了不同寻常的要求.

师：请你根据所学的一次函数知识点，结合题目条件，提出问题并解决问题.

条件：直线l1：y=x+3与过点A(3，0)的直线l2交于点C(1，m)，与x轴交于点B．

经过几分钟的思考，学生提出了如下问题：

①求点B，E，C的坐标．

②求直线l2的解析式以及点D的坐标．

③求线段AB，BC，AC，CD，DE．

④求△ABC的面积．

⑤当直线l2在直线l1的上方时，求x的取值范围；当直线l1在直线y=4上方时，求x的取值范围.

师：请同学们再思考一下，从图象变换的角度能否提出什么问题？

经过几分钟的思考，学生提出了如下问题：

⑥将l1向下平移3个单位，平移后直线的解析式是什么？

⑦将l2绕着点O逆时针旋转90°，求旋转后直线对应函数的表达式.

⑧将l2绕点A逆时针旋转，当l2将△AOD面积分成相等的两部分时，求旋转后直线的解析式．

⑨将l2绕点A逆时针旋转，当l2将△AOD周长分成相等的两部分时，求旋转后直线的解析式．

师：大家提出的问题很好，下面请思考：(1)这些题目如何解答？(2)它们涉及哪些知识和方法？

生1：1-4题难度不大，主要涉及求解析式、求交点、求线段长度以及求面积．

生2：第5题涉及数形结合思想，可以结合图象或根据解析式来求解．

生3：第6题难度不大，涉及图象的平移，得出正比例函数．

生4:7-9题略有难度，直线的旋转关键要先找点及其对应点的位置，然后求出坐标，最后利用待定系数法求解析式．

设计说明多年的学习生活使得学生们早已习惯于教师提出问题，学生解决问题的教学模式.而本节课在上课的开始，笔者提供一个2020年南通市中考题，隐去了题目原带的问题，让学生自己读完条件后提出问题.这与平时正常的教学相比具有很大的差异，或许学生一开始会有所不适应，提出的问题会没有章法，没有价值，但在教师的引导、干预下，学生提出的问题可以很有价值，如第7个问题就是2020年南京市的一个中考题，教师这时就可以充分肯定学生提出问题的能力，再引导学生有效地去解决问题．在教学中真正让学生感受到在学习数学时自主提出问题的重要性和必要性，从而做到教学中的有效渗透．

2 增加原题条件 合作提出问题

在原题基础上对条件略作增加或改变，让学生合作研究问题的提出可以启发其对原题的深度探究．

师：在上面题目条件的前提下，请你结合本题条件，提出问题并解决问题.

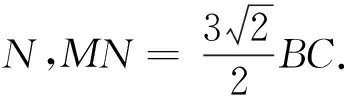
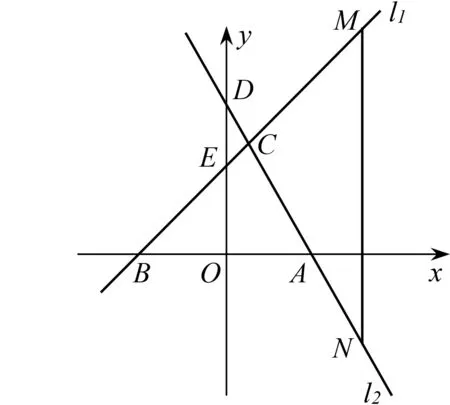
图2

笔者要求学生小组合作，此时教师在小组中巡视、引导、点拨．稍后由小组代表提出了具有本组代表性的问题：

⑩求点M，N的坐标．

师：若一次函数y=kx+1的图象为l3，且l1，l2，l3不能围成三角形，能否提出什么问题？

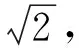
师：若点F为x轴上一动点，连结EF，将EF绕点E逆时针旋转90°得EG，连结DG，能否提出什么问题？

师：结合了老师和大家的智慧，我们提出了有一定深度的好问题，这些题目提出后该如何解答？它们涉及哪些知识和方法？

第1组代表：10-13题难度不大，主要涉及分类讨论的思想．

第2组代表：第14题有点难度，求助老师来解决．

设计说明对原题增加条件的目的是让学生小组合作，教师在巡视过程中适时引导点拔，让学生小组活动得以有效地逐层深入，培养学生提出一些较为复杂的、有深度的问题的能力，师生可以一起讨论提出问题及解决问题．对于第14题，教师还可以借助几何画板动态演示点F的变化过程，一方面培养学生从运动的角度提出有一定深度的问题，另一方面可以直观地帮助学生解决问题．

3 对问题教学的思考和认知

通过这样的教学，我们发现，学生分析数学题目的角度有了明显的改变，思考过程中经常会问“为什么”．这种问题意识犹如一棵大树的枝叶，向四周延伸，生机勃勃．

希尔伯特曾说“问题是数学的心脏，方法是数学的行为，思想是数学的灵魂”．发现和提出问题是一切创新的起点，也是获取新数学知识的关键基础，具有十分重要的意义．学会提出问题、解决问题，是学生学习的必要内容；从学生数学能力的培养上来讲，学会提出问题往往比学会解决问题更重要，因为提出问题孕育着对学生创新思维和创新能力的培养．[2]在数学复习课教学中，教师应梳理已学的知识点并形成思维导图，多研究典型例题的改编，引导学生学会思考、学会提出问题．

教师研究题目的水平有多高，学生能力的提升就有多高！通过问题教学的实践，总结出如下经验.

3.1 问题教学应将学生带入情境

以问题研究为突破的数学课堂教学模式的首要问题是要创设良好的问题情境，而且要将学生带入情境．为此，教师就要精心设置问题环境，让学生问题意识从无到有，从少到多．关键还在于使学生身临其境，提高学生的学习兴趣，让学生学得轻松而愉悦．为此还需注意：问题空间大小有度，应符合学生的最近发展区，好的问题既能穿针引线又能以点带面；其次，选择的问题要尽量回归课本，返璞归真．

3.2 问题教学要创设良好的课堂氛围

在数学课堂中，教师的主要任务就是组织教学和教育学生，而良好的课堂氛围是完成教育教学任务的重要前提．知识应该通过学生活动、体验、探究来获得，只有让学生主动地学，使学生“乐学”“会学”，才能有效提高教学质量．为此，在教与学的过程中，师生双方要形成学习共同体，相互交流、探讨、分享彼此的思考、见解和智慧．

3.3 问题教学的核心是提高学生素养

教育部在《关于全面深化课程改革落实立德树人根本任务的意见》中明确指出：学生应具备适应终身发展和社会发展需要的必备品格和关键能力，突出强调个人修养、社会关爱、家国情怀，更加注重自主发展、合作参与、创新实践．我们在教学中应牢记核心素养的培养目标，努力创设让学生终身受益、终身难忘的学习经历．在核心素养的大背景之下，我们的教学不能只是为了传授知识，更要注意引导学生学会思考，培养学生良好的思维习惯，提升学生的数学素养．以问题研究为突破的数学课堂教学新模式是与新课程的要求相适应的，这种模式旨在突出学生的情感体验，突出学生的主动参与，突出学生的大胆创新，是培养学生合作能力与创新思维能力十分有效的教学方法．

3.4 问题教学中要遵循的几个基本原则

问题教学可以把教师见过的习题、例题、考题作为素材展开活动，但应遵循以下几个原则：

(1)主体性原则：问题教学必须把学生当作实践和知识的主体来对待，最大限度地发挥学生的主观能动性．[3]在探究中培养学生互相学习和团队合作的精神作风；(2)探索性原则：教师的教育、教学活动应富有深刻的内涵，通过创设问题情境，让教师及学生产生互动和共鸣，在探索中解决疑惑，引导学生在亲身体验中探求新知，发现问题；(3)发展性原则：问题教学要充分考虑到学生数学思维能力的提高，创新意识的提升，数学素养的发展，这就必须将视角放到学生人生价值和人格塑造上来，为学生将来的生存与发展的大局着想．