基于波形相似度因子的双馈风电场送出线路单相接地保护*

史卓鹏, 孔祥敏 王亚臣

(国网山西省电力公司经济技术研究院，山西 太原 030024)

0 引 言

近年来大规模风电相继并网，然而风资源的随机波动性、场站的时空耦合性、电网运行方式的复杂多变性，显著增大了送出线路单点故障引发全网系统性事故的风险，威胁电网的安全稳定运行。因此，有必要深入研究双馈感应发电机(DFIG)故障机理及其对保护造成的影响，确保双馈风电场送出线路保护能够正确、可靠地动作[1-5]。

目前，许多学者针对风电场送出线路保护进行了深入研究。文献[6]研究了国内外大规模风电接入电网后原有继电保护产生的问题以及优化方向。文献[7]阐述了风电场的弱电源特性将引起保护的不正确动作。文献[8-9]指出双馈风机的故障暂态特性使故障电流频率发生变化，引起保护的不正确动作。文献[10]通过风电场侧电流幅值衰减程度远大于系统侧电流这一特性构造基于峰值与谷值差值的方向元件新原理。文献[11]利用故障前后工频电流相角差构造方向保护判据，但相角提取利用了全周傅里叶算法，其计算准确性受转速频率分量影响。

针对上述问题，本文提出一种基于波形相似度因子的双馈风电场送出线路单相接地保护方法。在分析风电送出线路故障后故障电流暂态特性的基础上，建立风电送出系统的0模瞬时值模型。利用区内外故障时模型差异特征构造0模电压相似度因子，进行故障定位。仿真结果验证了该方法在各种单相接地故障情况下均能正确识别区内外故障。

1 故障特性

并网型DFIG主电路拓扑结构如图1所示。

图1 DFIG并网系统等效电路

电网故障时，DFIG转子绕组中产生较大的过电流，导致转子侧变流器受损。为了避免过电流威胁，投入撬棒电路为过电流提供通路。撬棒投入后，相当于增大了转子电阻，转子时间常数变小，进而改变了DFIG的电磁暂态特性。

定转子绕组均采用电机惯例。忽略磁饱和的影响，在abc三相坐标系中，三相短路故障时，DFIG定子磁链分为强制分量部分和自由分量部分，表示为

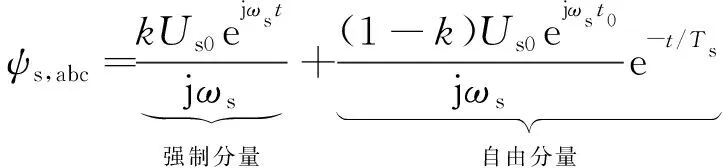
(1)

式中：k为电压跌落深度；Us0为正常电压幅值；ωs为系统同步角速度；Ts为定子衰减时间常数。

DFIG转子磁链分为强制分量部分和自由分量部分。转速暂态分量衰减完成以后，利用异步电机数学模型求解转子磁链为

(2)

式中：Rr为转子绕组电阻；s为转差率；ωr为转子角速度。

撬棒投入需要经过一定延时Tc，撬棒动作瞬间磁链守恒。撬棒投入后转子磁链可表示为

(3)

根据式(3)的磁链方程，可求解定子电流：

通过式(4)所得故障电流解析表达式分析可以得知：

(1) 故障初始阶段，定子电压突然跌落会在定、转子绕组中激起很大的直流衰减分量，该分量又会令两侧绕组中相应地产生转速频率分量。后者主要由对侧直流分量产生的磁链激发，按照本侧绕组衰减时间常数衰减，其大小与故障跌落程度、故障发生时的运行工况及转子侧变流器的控制策略均有关系。

(2) 撬棒保护投入后，定子电流中存在直流衰减分量和转速频率衰减分量。其中转速频率分量迅速衰减，其时间常数为转子衰减时间常数；直流分量以定子衰减时间常数缓慢衰减直至为零。由于撬棒电阻阻值远大于定子电阻阻值，因此转速频率分量衰减速度快于直流分量的衰减速度。

综上可知，风电侧故障电流频率发生偏移，其主要频率分量随短路前机组的转速变化，不再保持工频。因此，受转速频率分量的影响，工频傅里叶算法精度无法保证，或将导致保护动作性能下降，甚至发生拒动、误动。

2 基于波形相似度因子的送出线路单相接地保护方法

2.1 区内外故障时特征分析

风电送出系统0模分量等效网络如图2所示。其中Lw0为风电场送出变压器的等效0模电感；Rs0、Ls0分别为交流系统的等效0模电阻和0模电感；Rl0、Ll0分别为风电送出线路的0模电阻和0模电感；iw0、is0分别为风电侧和系统侧的0模电流；uw0、us0分别为风电侧和系统侧的0模电压。

图2 风电送出系统0模等效电路

下面分别对区内外单相接地故障时的特征展开分析。

当风电送出线路发生区内单相接地故障时，根据图2可以写出风电侧和系统侧0模电压的表达式：

(5)

(6)

由式(5)、式(6)可知，风电送出线区内故障时，线路两端保护安装处0模电压测量值为其背侧等效网络上的电压降，即此时0模电压反映保护背侧的风电场等效0模模型特征。

定义电压波形相似度因子：

(7)

式中：uw0为风电侧0模电压实际采样值构成的矢量；u′w0为送出线路风电侧的基准电压矢量，u′w0=-Lw0diw0/dt；us0为系统侧0模电压实际采样值构成的矢量；u′s0为送出线路系统侧的基准电压矢量，u′s0=-Rs0is0-Ls0dis0/dt。

区内故障时，保护安装处0模电压测量值即为背侧系统模型上的电压降，uw0=u′w0，us0=u′s0，两侧实测电压与基准电压波形相同，此时有kw=1，ks=1。

当风电端背侧发生区外单相接地故障时，线路两侧0模电压表达式为

(8)

(9)

将式(8)、式(9)代入式(7)可知，风电侧保护安装处0模电压测量值为送出线路及受端交流系统等效模型上的电压降，uw0≠u′w0，因此风电侧的实测电压与基准电压波形相异，kw<1。而系统侧保护安装处的0模电压测量值为其背侧系统模型上的电压降，us0=u′s0，因此系统侧实测电压与基准电压波形相同，ks=1。

同理，系统端背侧的受端系统发生区外单相接地故障时，线路两侧的0模电压表达式为

(10)

(11)

风电侧保护安装处的0模电压测量值为背侧电感上的电压降，uw0=u′w0，因此风电侧的实测电压与基准电压波形相同，kw=1。而系统侧保护安装处的0模电压测量值为对侧系统模型上的电压降，us0≠u′s0，因此系统侧实测电压与基准电压波形相异，ks<1。

2.2 保护判据

根据2.1节分析可知，当送出线路区内发生故障时，风电侧与系统侧保护安装处的0模电压反映背侧系统0模电压降，两端电压波形相似度因子均为1。当送出线路区外发生故障时，故障一侧保护安装处的0模电压反映其对侧系统的0模电压降，即故障侧电压波形相似度因子小于1。

因此可构建保护动作判据：

(12)

根据上述分析，本文提出基于波形相似度因子的双馈风电场送出线路单相接地保护原理，其实现的具体步骤如下。

步骤1：获取风电送出线路两端保护安装处的0模电压、电流采样值。

步骤2：将0模电压、电流采样值代入式(12)中，计算送出线路两端0模电压波形相似度因子。

步骤3：若电压波形相似度因子大于动作门槛，说明风电送出线路区内发生故障，反之则为区外故障。

本文考虑测量误差等因素的影响，将门槛值定为kset=0.5。

3 仿真验证

风电送出系统如图3所示。风电场由300台完全相同的DFIG并联组成，每台风机的额定容量为1.5 MW，并且按照额定出力运行。风电送出系统主要参数如表1所示。

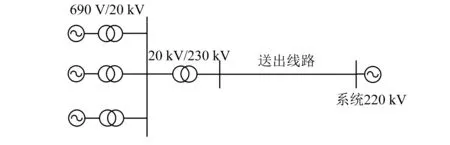
图3 风电送出系统

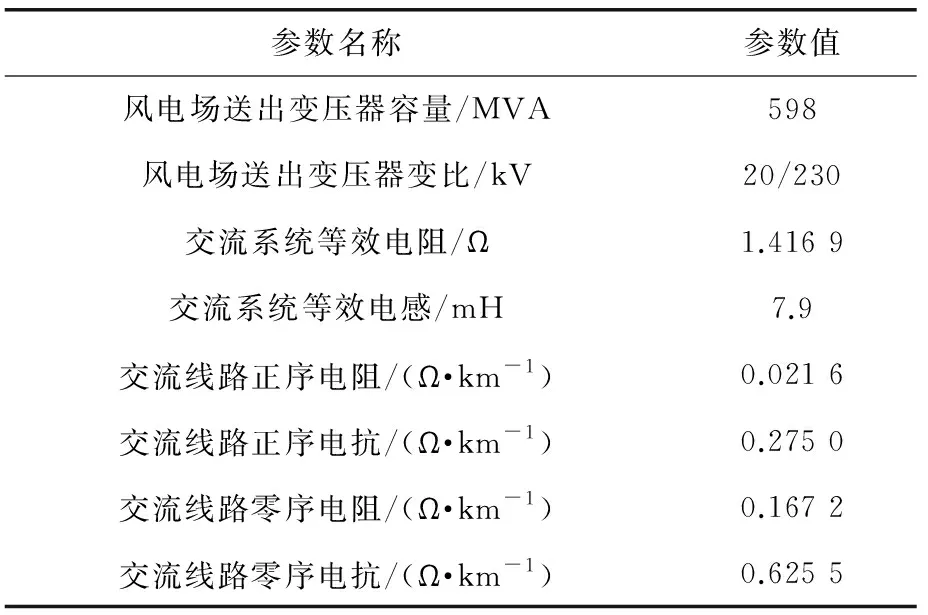
表1 风电送出系统主要参数

3.1 区内单相接地故障

t=1.4 s时在风电场送出线路内部设置A相单相接地故障，故障持续0.1 s，过渡电阻分别为0、300 Ω。测量风电送出系统中风电侧和系统侧0模电流和0模电压值，计算不同故障场景中送出线路两端0模电压波形相似度因子，结果如图4所示。

图4 区内经不同过渡电阻单相接地故障时0模电压波形相似度因子

由图4可知，区内故障时，风电侧和系统侧的0模电压波形相似度因子数值波动很小，均接近1，大于保护门槛值0.5，保护正确动作，且不受过渡电阻影响。

3.2 区外单相接地故障

t=1.4 s时分别在送出线路风电侧和系统侧背侧系统设置A相单相接地故障，故障持续0.1 s，过渡电阻分别为100、300 Ω。测量风电送出系统中风电侧和系统侧0模电流和0模电压值，计算不同故障场景中送出线路两端0模电压波形相似度因子，结果如图5、图6所示。

图5 送出线路风电侧背侧系统经不同过渡电阻单相接地故障时0模电压波形相似度因子

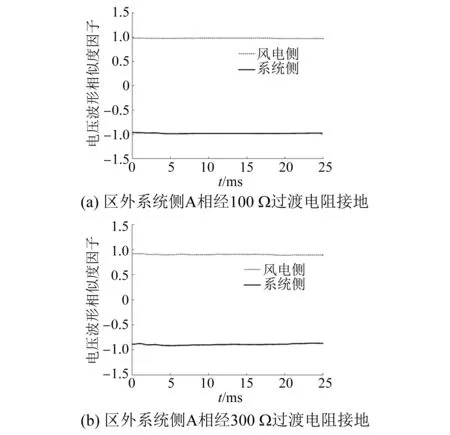
图6 送出线路系统侧背侧系统经不同过渡电阻单相接地故障时0模电压波形相似度因子

由图5、图6可见，风电受端交流系统故障时，系统侧0模电压波形相似度因子数值波动很小，稳定在1附近。风电侧0模电压波形相似度因子在A相经100 Ω过渡电阻接地，t=10 ms时有最大值0.258，小于保护门槛值0.5，保护不动作。风电场内部故障时，风电侧0模电压波形相似度因子值波动很小，稳定在1附近。系统侧0模电压波形相似度因子在过渡电阻300 Ω，t=47 ms时有最大值-0.867，远小于保护门槛值0.5。因此，区外故障时，保护可靠不动作。

4 结 语

本文提出了一种基于0模电压波形相似度因子的风电送出线路纵联保护新原理。仿真结果表明，该方法具有如下特点：

(1) 建立了风电送出系统的0模瞬时值模型，并利用区内外故障时模型差异特征，实现故障的准确定位。采用时域信息，克服了利用某一频带分量检测故障时可靠性不高的问题。

(2) 不受过渡电阻影响，灵敏度高，能够可靠地识别区内、区外故障。