变温热源Lenoir循环功率和效率优化
2021-07-20王瑞博戈延林陈林根吴志祥
王瑞博,戈延林,陈林根,吴志祥
(1.武汉工程大学 热科学与动力工程研究所,武汉 430205;2.武汉工程大学 机电工程学院,武汉 430205)
有限时间热力学(Finite Time Thermodynamics,FTT)理论自从应用于各种循环和过程的性能分析和优化以来,相关研究取得了丰硕的成果[1-4]。根据循环的性质,热机循环可以分为定常流循环[5-6]和往复式循环[7-10]。对于定常流热机循环,由于高、低温热源温度变化可以使循环接近实际热机的工作状态,因此,一些学者对变温热源条件下的定常流循环进行了研究。Feidt等[11]研究了变温热源内可逆定常流Carnot循环在潜热和显热2种余热回收形式下的循环性能。Yasunaga等[12]采用一种新的性能评估方法对变温热源条件下的内可逆海洋热能转换系统的功率和热效率特性进行了研究,分析了工质热容率和总传热系数对热机性能的影响。
早在1860年,Lenoir就提出了Lenoir循环模型[13]。从循环过程来看,Lenoir循环缺少压缩过程,循环模型看起来像一个三角形,因此也被叫做“三角循环”。Lenoir循环是一种典型的大气压压缩式热机循环,热机在工作中所需的压缩过程利用大气压来实现。Georgiou[14]最早采用经典热力学理论对简单、回热和修正回热式定常流Lenoir循环进行研究,分析了气体常数和温比对循环性能的影响,并将Lenoir循环性能与定常流Carnot循环性能进行了比较。
应用FTT理论,一些学者分别对往复式Lenoir循环和定常流Lenoir循环进行了研究。周骏乐等[15-16]在不计任何损失的基础上,研究了工质比热容随温度线性变化和非线性变化时的可逆往复式Lenoir循环,导出了循环输出功和效率的表达式,分析了循环各参数对输出功和效率特性的影响。张子煜等[17]在考虑传热损失的基础上,建立了工质线性变比热容内可逆往复式Lenoir循环模型,分析了传热相关常数和工质比热容对循环性能的影响。
Shen等[18]在考虑传热损失的条件下建立了内可逆定常流Lenoir循环模型,分析了热源温比和总热导率对功率和热效率特性的影响,给出了最大功率和最大热效率对应的最优热导率分配。Ahmadi等[19]基于NSGA-Ⅱ算法对内可逆定常流Lenoir循环生态学性能系数和热经济进行了两目标优化,给出了相应目标函数及决策变量的最优值。王瑞博等[20]在文献[18]的基础上,进一步考虑内不可逆性,建立了不可逆Lenoir定常流循环模型,分析了总热导率、热源温比和不可逆损失对功率和效率特性的影响。
以上文献均为在高温和低温热源温度恒定条件下对定常流Lenoir循环性能的研究,本文将在文献[14,18]的基础上,建立热源温度变化条件下的内可逆定常流Lenoir循环模型,研究热容率匹配对循环最大功率和最大效率的影响。
1 循环模型
图1给出了变温热源条件下定常流内可逆Lenoir循环的T-s图。其中,1→2为定容吸热过程,2→3为绝热膨胀过程,3→1为定压放热过程,热流体和冷却流体的进口温度分别为THin和TLin,出口温度分别为THout和TLout。
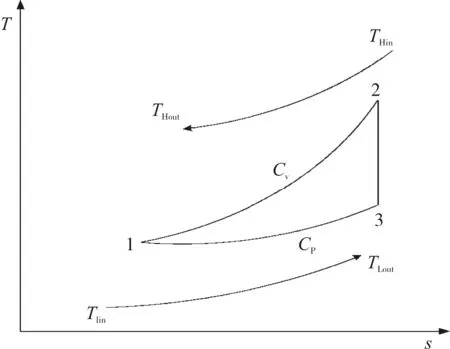
图1 变温热源条件下的内可逆Lenoir循环T-s图
假设高、低温热源与工质间的传热服从牛顿传热定律,由工质性质和换热器理论可得循环吸、放热率分别为:
QH=Cwf1(T2-T1)=CHminEH1(THin-T1)(1)
QL=Cwf2(T3-T1)=CLminEL1(T3-TLin)
(2)
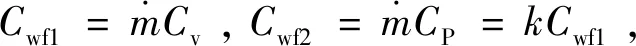
(3)
(4)
式中:NH1、NL1为换热器的传热单元数;CHmax、CHmin为CH和Cwf1的较大或较小者;CLmax、CLmin为CL和kCwf1的较大或较小者。其表达式分别为:
NH1=UH/CHmin
(5)
NL1=UL/CLmin
(6)
CHmax=max{CH,Cwf1}
CHmin=min{CH,Cwf1}
(7)
CLmax=max{CL,kCwf1}
CLmin=min{CL,kCwf1}
(8)
2 循环性能分析与优化
2.1 循环输出功率和效率表达式
根据热力学第二定律,工质经过一个循环过程,总熵变为0,即有:
Cvln(T2/T1)-CPln(T3/T1)=0
(9)
由式(9)可得:
(10)
由式(1)和(2)可得:
(11)
(12)
联立式(10)至(12)可得关于T1的方程:
T1=(CLminEL1TLin-kCwf1T1)·(CLminEL1-kCwf1)-1·{[(CHminEH1/Cwf1)(THin-T1)+
(13)
由式(1)、(2)、(11)、(12)和(13)可得循环输出功率和效率表达式分别为:
P=[CHminEH1(THin-T1)(CLminEL1-kCwf1)-kCLminEL1Cwf1(TLin-T1)]×[CLminEL1-kCwf1]-1
(14)
η=[CHminEH1(THin-T1)(CLminEL1-kCwf1)-kCLminEL1Cwf1(TLin-T1)]×[CHminEH1(CLminEL1-
kCwf1)(THin-T1)]-1
(15)
当CH=CL→∞时,将其代入式(3)、(4)和(13),可得恒温热源内可逆定常流Lenoir循环2个换热器有效度EH、EL和关于T1的表达式,分别为:
EH=1-e-NH
EL=1-e-NL
(16)
T1-ELTL=(1-EL)[EHTH+
(17)
式中:NH和NL为热源温度恒定条件下2个换热器的传热单元数。式(16)和(17)为文献[18]中的式(3)和(15)。根据式(14)至(17),通过数值解法,可得文献[18]中的恒温热源内可逆Lenoir循环的输出功率和热效率特性关系。
2.2 高、低温侧换热器热导率为定值时的功率和效率特性分析
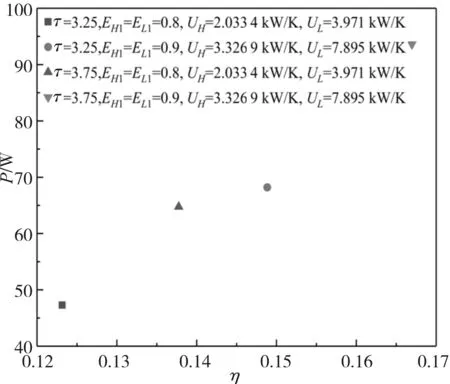
图2 UH和UL给定时的P-η特性
由于Lenoir循环缺少绝热压缩过程,是一种3分支循环,关于循环压力比的约束条件缺失,因此其无法得到功率和热效率的基本优化关系。当UH和UL一定时,由式(3)至(6)和式(13)至(15)可以看出,当给定相应的换热器有效度,且循环热源进出口温度固定时,循环输出功率和效率为一个固定的值。由图2可以看出:当EH1和EL1分别取0.8和0.9,热源进口温比τ(τ=THin/TLin)分别取3.25和3.75时,P-η为一个确定的点,P和η随着τ和UH、UL的增大而增大。
2.3 高、低温侧换热器热导率可优化分配时的功率和效率优化
当UH和UL变化时,P和η也会发生改变。因此,可对高、低温侧换热器热导率进行优化,并得到相应的功率和热效率。假设2个换热器热导率之和为定值:
UL+UH=UT
(18)
UH=(1-uL)UT
UL=uLUT
(19)
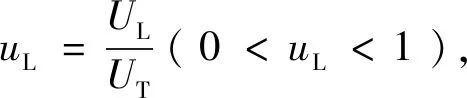
(20)
(21)
联立式(13)至(15)和式(20)至(21),通过数值解法,可得热源温度变化条件下内可逆Lenoir循环P与uL以及η与uL的特性关系。
当2个换热器热导率可进行优化分配时,由式(13)至(15)和式(20)至(21)可以看出,τ和UT对P-uL和η-uL的特性关系有一定影响。图3给出了给定不同τ条件下,UT对P-uL和η-uL特性关系的影响。
从图3中可以看出,P-uL和η-uL为类抛物线型曲线,即存在最大输出功率Pmax和最大热效率ηmax,以及相应的最优热导率来分配uLP(opt)和uLη(opt);当τ一定时,随着UT的增大,Pmax和ηmax增大;当UT取值较大时,η-uL类抛物线逐渐趋于平坦,这表明当UT超出一定取值范围时,uLη(opt)的取值范围增大。
表1给出了不同τ和UT条件下的Pmax和ηmax以及相对应的uLP(opt)和uLη(opt)。从表1可以看出:当τ给定时,随着UT的增大,Pmax和ηmax增大;uLP(opt)和uLη(opt)先减小后增大;当UT给定时,随着τ的增大,Pmax、ηmax、uLP(opt)和uLη(opt)增大;当τ或UT给定时,始终有uLη(opt)>uLP(opt)。
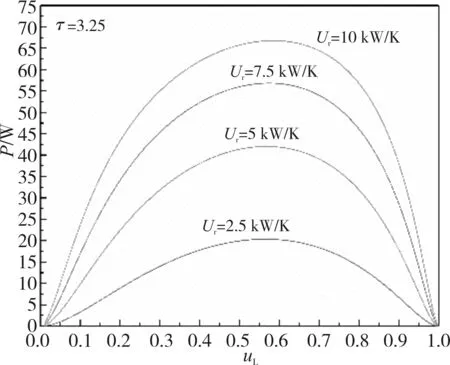
(a)τ=3.25时UT对P-uL特性的影响
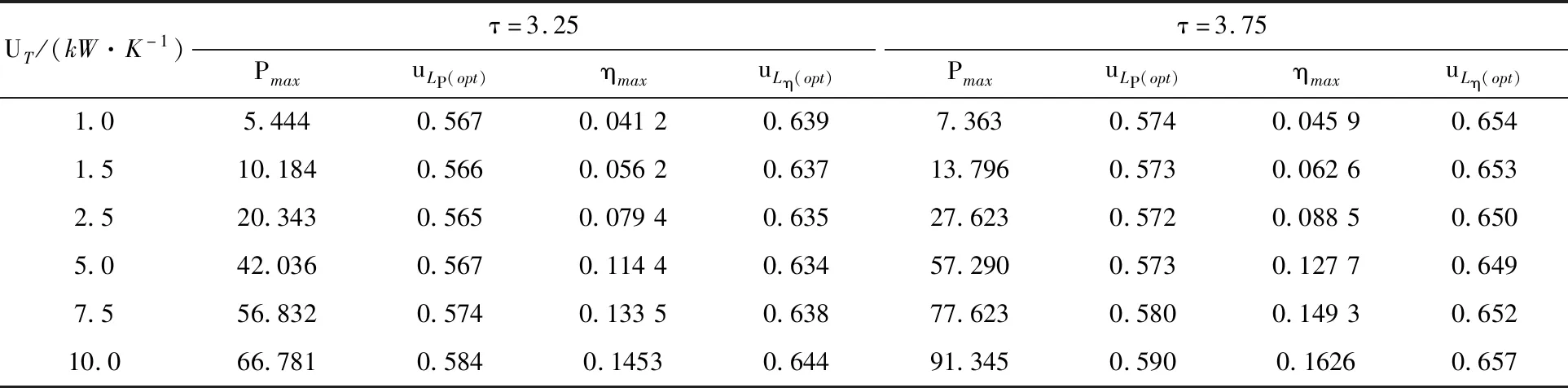
表1 不同τ和UT值时相应的Pmax、ηmax、uLP(opt)和uLη(opt)
图4和图5为Cwf1对Pmax-τ和uLP(opt)-τ特性的影响。从图4和图5中可以看出:当Cwf1给定时,随着τ的增大,Pmax和uLP(opt)增大;τ给定时,随着Cwf1的增大,Pmax和uLP(opt)减小。当τ=4,Cwf1为1、1.15和1.3时,Pmax分别为45.45、39.22和34.24 W,相应的uLP(opt)为0.563、0.557和0.553;Cwf1由1增大到1.3时,Pmax减小了约24.7%,uLP(opt)减小了约1.78%。
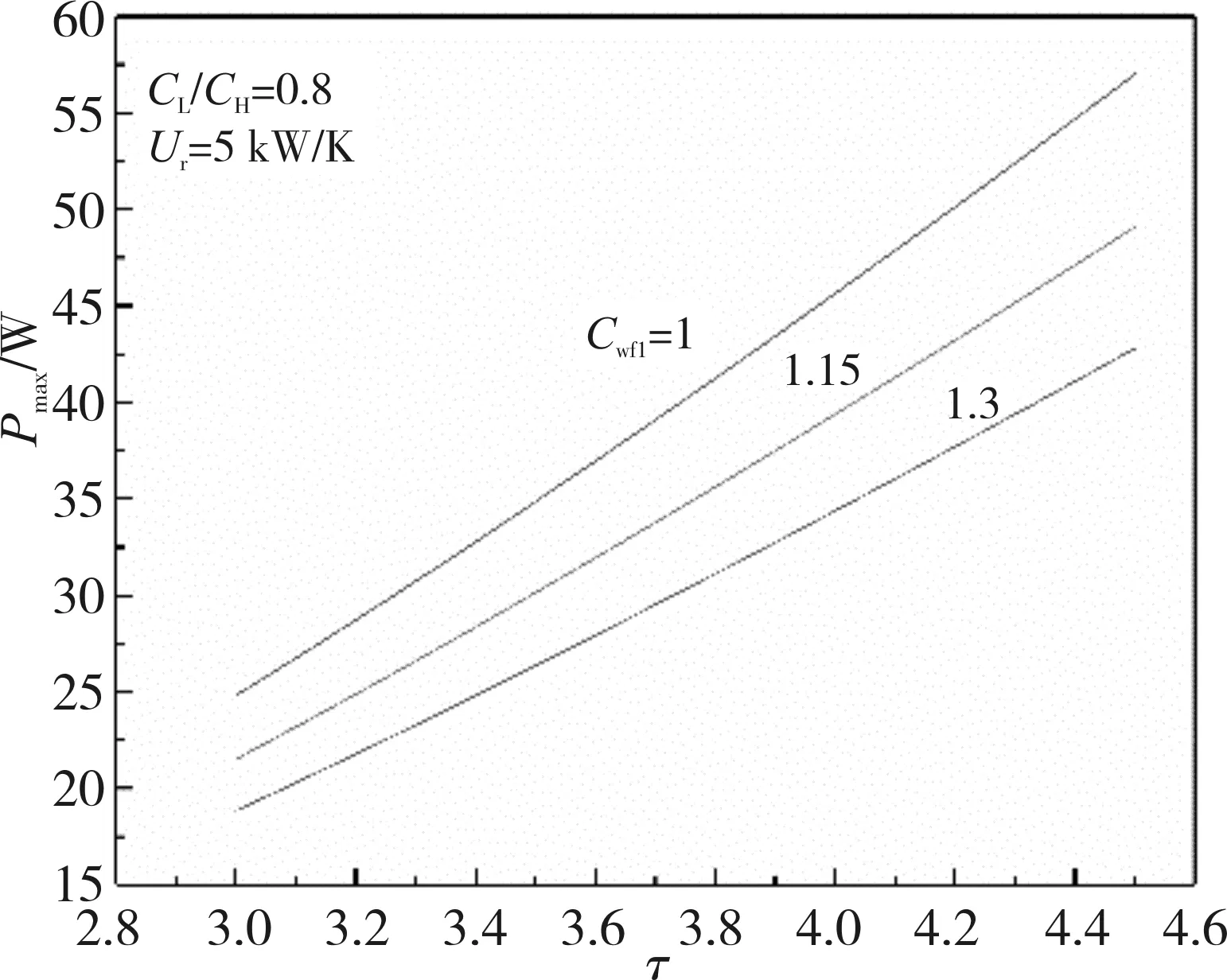
图4 Cwf1对Pmax-τ特性的影响
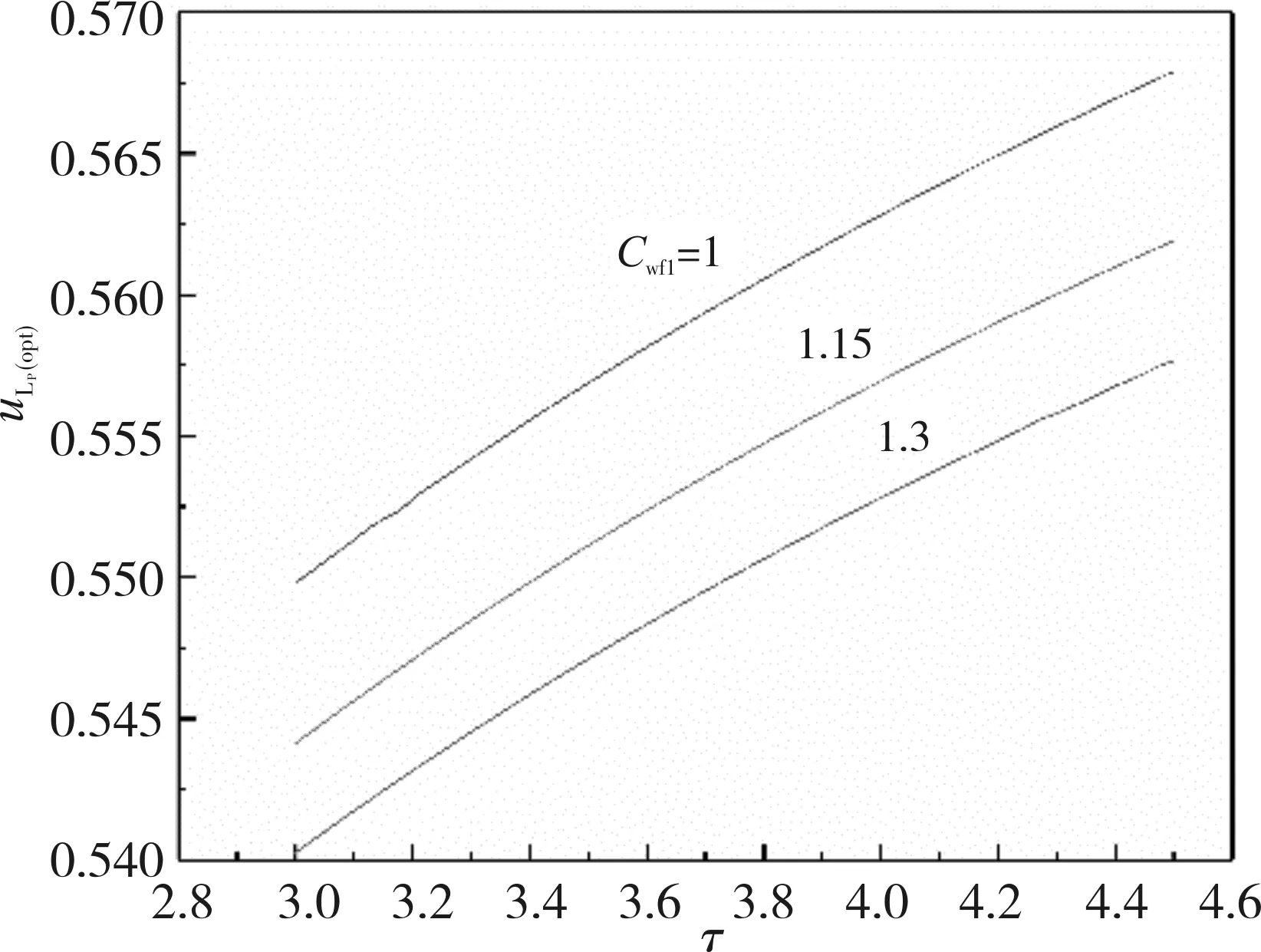
图5 Cwf1对uLP(opt)-τ特性的影响
2.4 热容率匹配优化
取CH=1.2,τ=3.25,UT=5 kW/K和CL/CH=0.8,以P为目标函数,uL为优化变量,研究CL/CH、UT和τ对Pmax-Cwf1/CH特性的影响。
图6、图7、图8给出了高、低温热源热容率之比CL/CH、UT和τ对Pmax-Cwf1/CH特性的影响。
图6为CL/CH对Pmax-Cwf1/CH特性的影响。从图6中可以看出,随着CL/CH的增大,(Pmax)max和(Cwf1/CH)opt增大,当CL/CH为0.8、1、2、3和5时,(Pmax)max分别为44.695、47.962、54.803、57.085和58.893 W,相应地,(Cwf1/CH)opt分别为0.42、0.46、0.54、0.58和0.59。CL/CH由0.8增大到5时,(Pmax)max增大了约31.8%,相应地,(Cwf1/CH)opt增大了约40.5%。图7为UT对Pmax-Cwf1/CH特性的影响。从图7中可以看出,随着UT的增大,(Pmax)max和(Cwf1/CH)opt增大,当UT为2.5、5、7.5和10 kW/K时,(Pmax)max分别为28.7、44.69、54.47和60.84 W,相应地,(Cwf1/CH)opt分别为0.29、0.42、0.48和0.52。当UT由2.5增大到10时,(Pmax)max增大了约111.99%,相应地,(Cwf1/CH)opt增大了约79.3%。图8为τ对Pmax-Cwf1/CH特性的影响。从图8中可以看出,随着Cwf1/CH的增大,Pmax-Cwf1/CH呈现先增大后减小,然后逐渐趋于平稳的类抛物线型变化,即存在Cwf1/CH的最优值(Cwf1/CH)opt使循环达到二次功率最大值(Pmax)max。随着τ的增大,(Pmax)max增大,相应地,(Cwf1/CH)opt保持不变。当τ为3.25、3.5、3.75和4时,(Pmax)max分别为60.84、71.84、83.34和95.3 W,相应地,(Cwf1/CH)opt为0.52,τ由3.25增大到4,(Pmax)max增大了约56.64%。
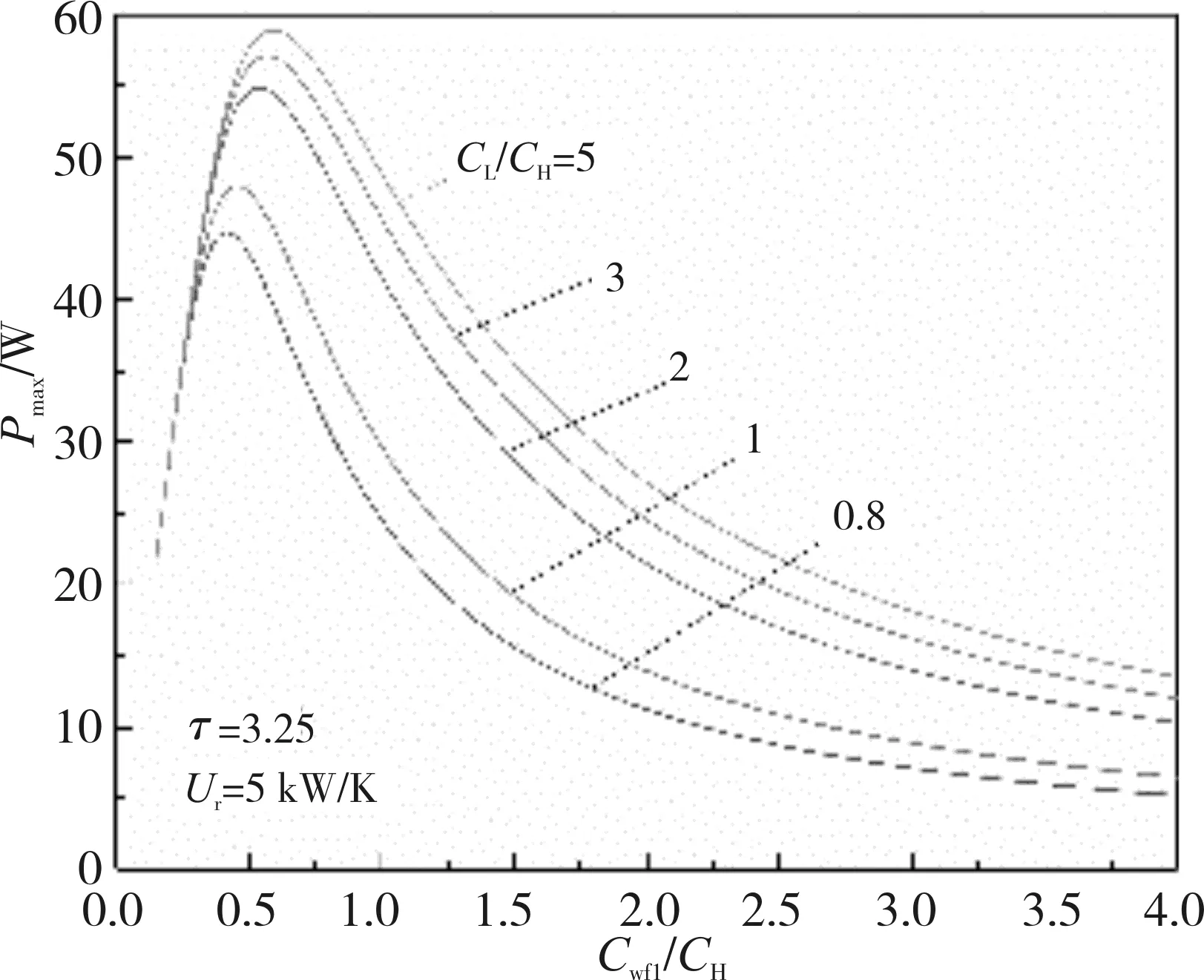
图6 CL/CH对Pmax-Cwf1/CH特性的影响
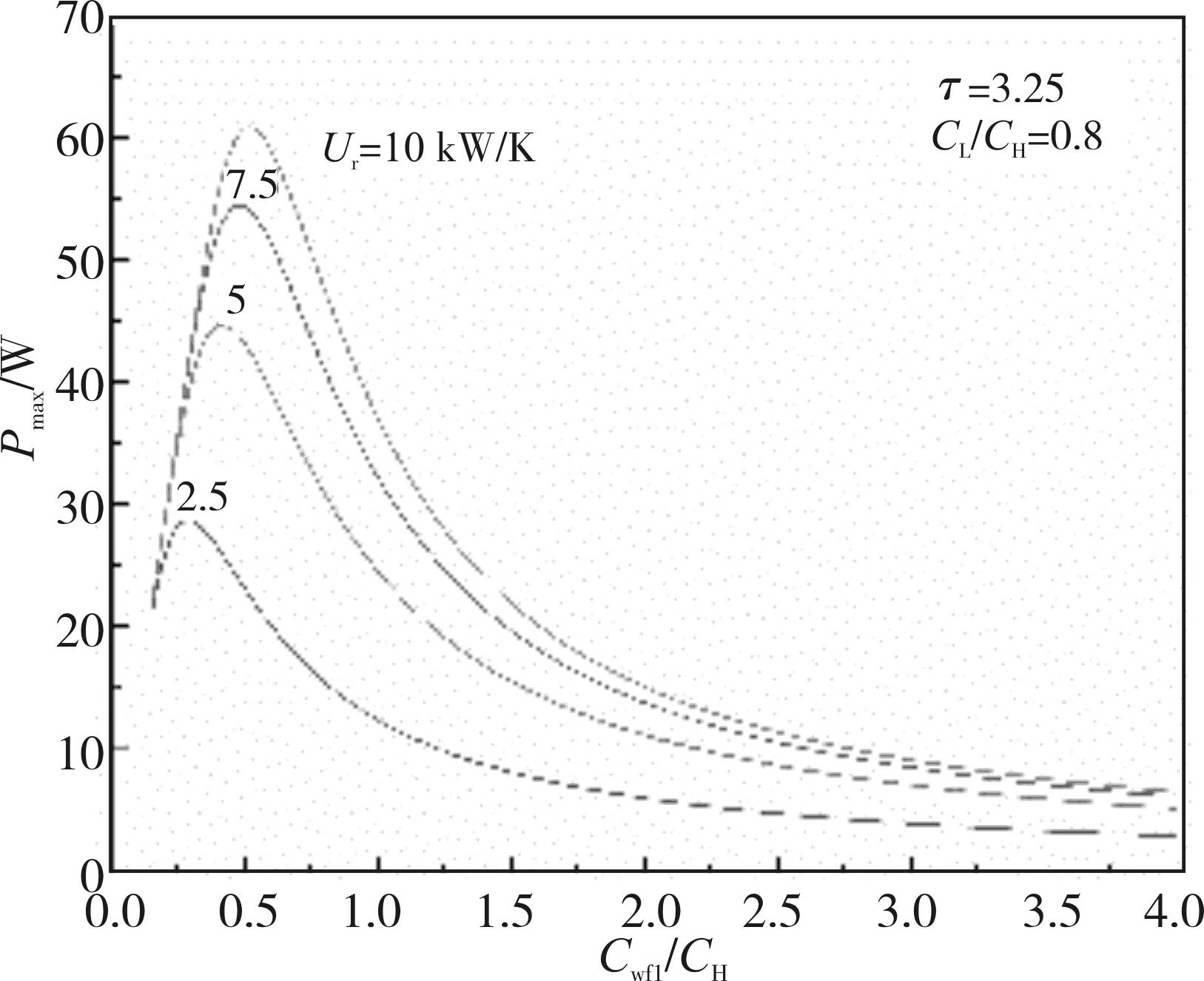
图7 UT对Pmax-Cwf1/CH特性的影响
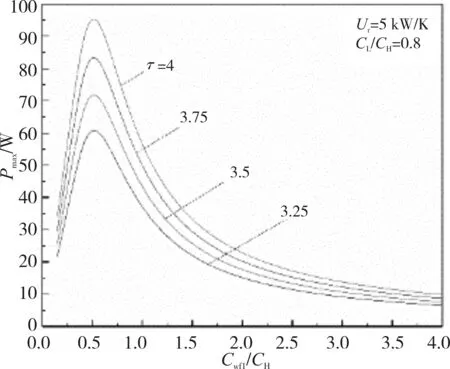
图8 τ对Pmax-Cwf1/CH特性的影响
3 结 论
本文应用FTT理论,在考虑传热损失的情况下建立了热源温度变化条件下的内可逆定常流Lenoir循环模型,导出了P-uL和η-uL特性关系,分析了UT、τ、Cwf1和Cwf1/CH对循环性能的影响,得出如下结论:
1)当UH和UL给定时,P-η为一个确定的“点”,随着τ和UH(UL)的增大,P和η增大;
2)当高、低温侧换热器热导率可进行优化分配时,P-uL和η-uL特性的影响均呈类抛物线型,存在uLP(opt)和uLη(opt),使循环达到Pmax和ηmax;
3)随着Cwf1的增大,Pmax和uLP(opt)减小,随着Cwf1/CH的增大,Pmax-Cwf1/CH呈现先增大后减小,然后逐渐趋于平稳的类抛物线型变化,即存在(Cwf1/CH)opt使循环达到二次功率最大值(Pmax)max。
