适用于板式支座的三元乙丙橡胶超弹性本构模型研究
2021-07-19吕鹏飞冯广庆杜雅丹李金航杨梦凯吴均淼陈勇前朱晓伟
吕鹏飞,李 仪,冯广庆,杜雅丹,李金航,杨梦凯,吴均淼,陈勇前,朱晓伟*
(1.河南工业大学 土木工程学院,河南 郑州 450001;2.中国工程物理研究院 成都科学技术发展中心,四川 成都 610200)
加劲板式橡胶支座是公路桥梁领域中常采用的一种支座形式,其主要由若干层橡胶板和薄钢板组合而成[1]。为了抵抗剪切变形,在各层橡胶板与钢板之间涂抹胶粘剂并加压硫化,二者可以牢固地粘接成为一体。相比于传统的天然橡胶和氯丁橡胶,三元乙丙橡胶(EPDM)的耐老化性能较好,且具有优良的低温动态性能[2-3]。但板式橡胶支座对橡胶与金属的粘结性能要求较高,而目前市场上EPDM与金属的粘结性能较差,因此我国现行行业标准JT/T 4—2019《公路桥梁板式橡胶支座》并未给出EPDM支座的设计参数。
为解决该问题,近期我国某研发中心成功完成了一种改性EPDM的试制,其与钢板的粘结强度远高于现行标准中的粘结强度指标,且耐低温和耐老化性能优异,具有良好的应用前景。随着计算力学的发展,有限元分析已成为板式橡胶支座设计中不可缺少的一部分,但目前适用于该新型改性EPDM材料的超弹性本构模型研究尚未开展,制约了后期有限元数值模拟的研究和工程化应用。
本工作针对目前橡胶领域常用的Mooney-Rivlin模型[2]、Neo Hooke模型[3]和Yeoh模型[4]3种超弹性唯像本构模型对其单轴拉伸试验数据的拟合效果进行对比研究,分析相应本构模型的适用性,并获取相关材料参数,为新型改性EPDM支座的有限元数值模拟计算研究奠定基础。
1 实验
1.1 主要试样与设备
新型改性EPDM标准试样,成都绿色能源与绿色研究中心提供。电子万能材料试验机,深圳三思科技有限公司产品。
1.2 性能测试
橡胶材料物理性能测试由第三方检测机构完成,其中橡胶与钢板粘结强度(90°剥离)为25 kN·m-1,远高于现行标准指标10 kN·m-1,耐低温和耐老化性能满足标准要求。
橡胶材料力学性能按照GB/T 528—2009《硫化橡胶或热塑性橡胶 拉伸应力应变性能的测定》进行测试,拉伸试样为Ⅱ型哑铃状,试样总长度为(75.0±0.5)mm,试样试验区长度为(20.0±0.5)mm、厚度为(20.0±0.2)mm。为了消除应力软化效应[5],先期对其进行3次循环加载,加载速率为50 mm·min-1,最大加载应变为500%。选取第4次拉伸应力-应变试验数据表征该橡胶材料的力学性能。
2 结果与讨论
2.1 拉伸性能
本次试验采用5个EPDM标准试样进行拉伸试验,名义应力-应变曲线如图1所示,可以看出5个试样的试验一致性较好。
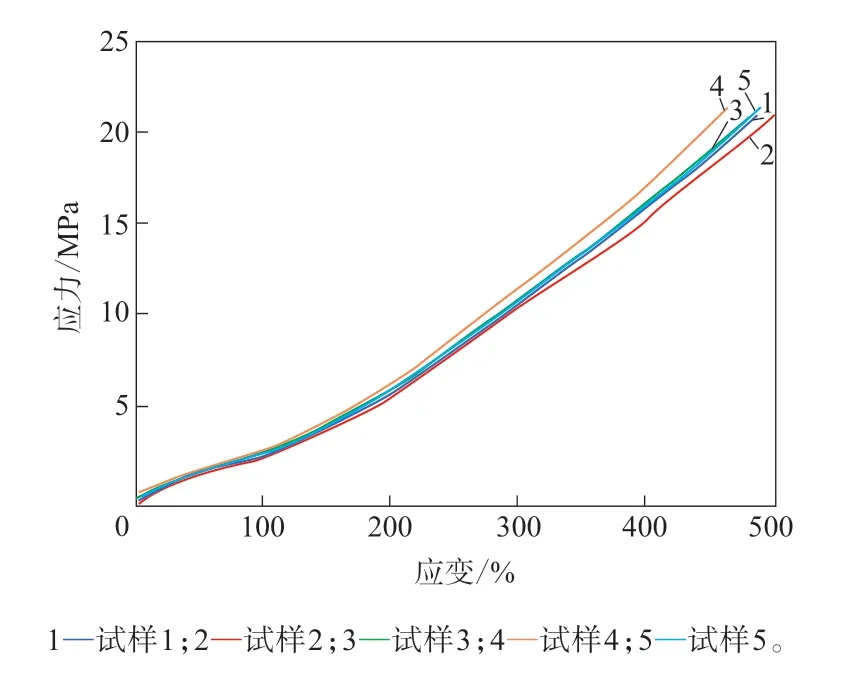
图1 EPDM标准试样的拉伸应力-应变曲线
2.2 适用于改性EPDM材料的超弹性本构模型
作为常用的有限元软件,ABAQUS软件的橡胶本构模型主要分为多项式和非多项式两大类,本工作主要针对有限元分析程序中常见的Mooney-Rivlin模型、Neo Hooke模型、Yeoh模型3种多项式唯像本构模型进行对比分析。上述本构模型均将橡胶的应变能密度函数(U)表示为变形张量的3个不变量的函数,由Rivlin于1951年提出的应变能表达式[6]见式(1)。
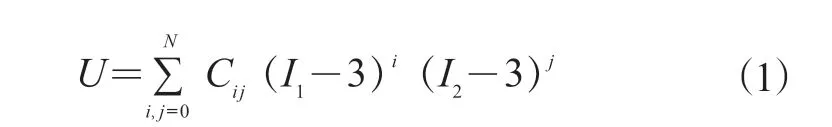
式中,Cij为材料参数,I1和I2分别为应变偏量第一和第二不变量,N为多项式的项数。在此基础上进行相应简化,即可提出适当的模型,如果只保留前两项,即为工程上常用的Mooney-Rivlin模型,如式(2)所示。
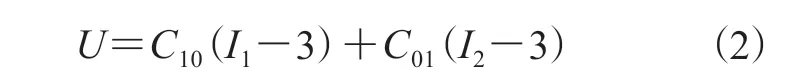
如果只考虑应变张量第一不变量,则称之为减缩型多项式,如只保留第1项即为Neo Hooke(N=1)模型,其表达式如式(3)所示。
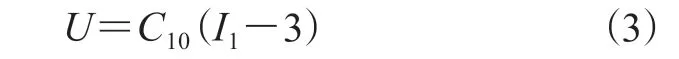
而Yeoh模型属于高阶应变能函数(N=3),其表达式如式(4)所示。
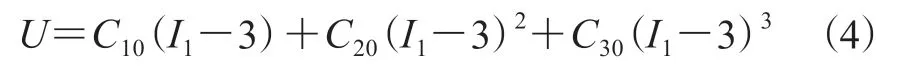
ABAQUS软件的Property模块为橡胶材料试验数据的拟合提供了平台[7-11],将EPDM材料单轴拉伸试验数据输入并选择相应的本构模型,即可拟合获取相应的材料参数。
ABAQUS软件对Mooney-Rivlin模型、Neo Hooke模型和Yeoh模型拟合所得的材料参数见表1。橡胶材料在ABAQUS软件中的这3种超弹性本构模型中都被视为不可压缩材料,因此在模型参数中,Di(表征材料几个方向是否可以压缩的量)均为零。
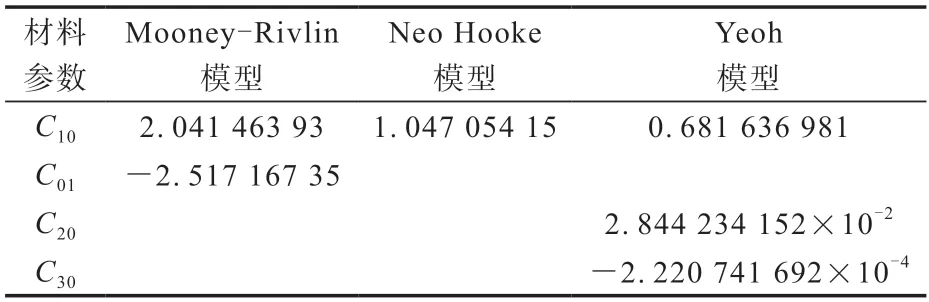
表1 3种超弹性本构模型下的材料参数
3种超弹性本构模型试验与拟合的应力-应变曲线对比见图2。
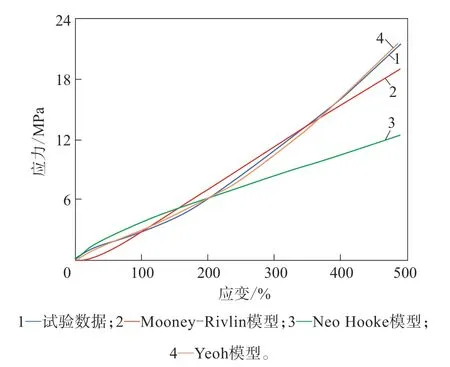
图2 3种超弹性本构模型试验与拟合的应力-应变曲线对比
从图2可以看出:在小变形下,3种模型对于改性EPDM材料的拟合均较为理想;随着应变增大,Neo Hooke模型拟合数据相对于试验数据的偏差逐渐增大,显然其不能用于大变形下的EPDM材料数值模拟,这主要是由于其只有单个材料常数,且与剪切模量相关,只能用于描述线性弹性行为,对于非线性弹性的力学行为并不适用[6];Mooney-Rivlin模型拟合数据相对于试验数据波动较大,Yeoh模型的整体拟合精度优于Mooney-Rivlin模型,这主要是由于Yeoh模型采用了高阶多项式,对于大变形下的EPDM材料模拟具有明显优势[4]。
2.3 EPDM标准试样的有限元分析
由上述可知,Yeoh模型对新型改性EPDM材料的超弹性力学行为拟合较好,为验证上述结论,基于ABAQUS软件采用橡胶试样原始尺寸建立仿真计算模型,试样模型及其网格划分如图3所示。橡胶材料泊松比设为0.499 75,网格类型为C3D8H实体杂交单元。将Yeoh模型作为EPDM拉伸试样的有限元分析模型,并代入获取的材料参数,开展同工况下的数值模拟计算。

图3 哑铃形EPDM标准试样的有限元模型及其网格划分
EPDM标准试样拉伸试验与有限元模拟见图4(应变为400%)。
从图4可以看出,试样变形特征与试验现象较吻合,标准区域的真实应力已达70 MPa以上。
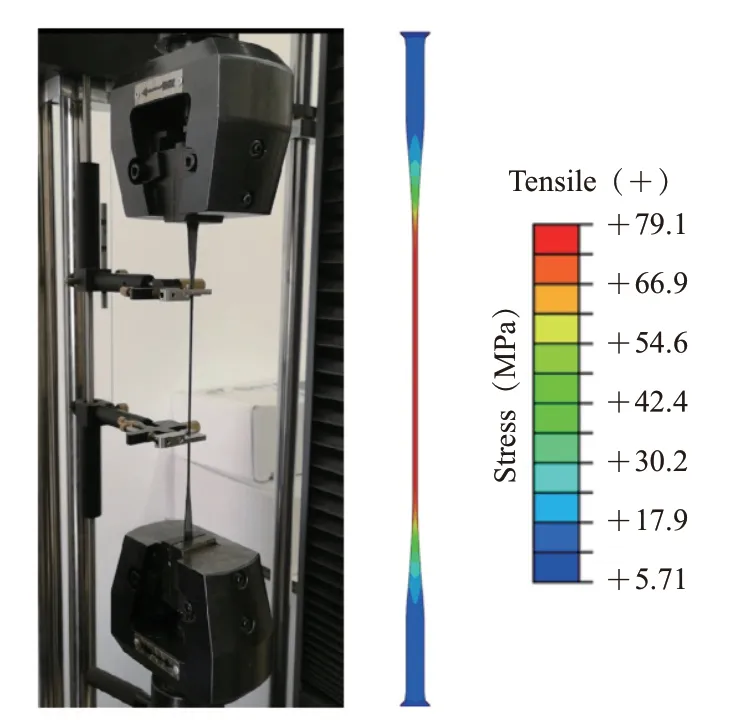
图4 EPDM标准试样拉伸试验与有限元模拟
EPDM标准试样拉伸试验与有限元模拟应力-应变曲线对比见图5。
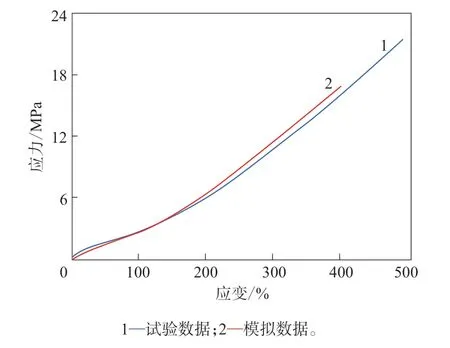
图5 EPDM标准试样拉伸试验与有限元模拟应力-应变曲线对比
从图5可以看出,试验数据与有限元模拟数据较吻合,尤其是在应变小于300%的范围内。这说明本工作拟合获取的Yeoh模型材料参数可以很好地表征新型改性EPDM材料的超弹性力学行为,为EPDM板式支座结构的数值分析奠定基础。
3 结论
本工作分析了3种超弹性本构模型对新型改性EPDM材料单轴拉伸试验数据的拟合效果。结果表明,高阶多项式的Yeoh模型(N=3),无论在拟合精度还是在适用范围上都比Mooney-Rivlin模型和Neo Hooke模型有较大优势,能够较好地拟合新型改性EPDM材料的超弹性力学行为,可为今后EPDM板式支座结构的数值分析奠定了基础。
