基于粒子群优化的自适应对比度增强算法在中子照相中的应用

曹旭宁 陈思泽 俞 杰 张连鑫 张早娣 李桃生

1（中国科学院合肥物质科学研究院核能安全技术研究所 合肥 230031）

2（中国科学技术大学 合肥 230027）

中子照相技术是一种重要的无损检测技术［1］，由于其穿透能力强、抗γ射线干扰以及对轻核素敏感等特点，弥补了传统X射线成像的不足，受到广泛关注［2］。然而由于中子相比X射线成像效率低，且中子源使用成本高昂，中子照相经常面临成像对比度不足的问题，限制了其在小型化、动态拍摄及三维CT成像等方向的发展和应用［3］。对比度图像增强算法在软件环境下直接对已成像图像进行处理，改善原图灰度分布，是一种解决中子照相对比度不足的有效技术方案，降低了图像质量对中子源和成像设备的依赖，成为中子照相技术的热点研究领域［4-5］。

目前，国内外学者在对比度增强算法领域已进行了大量的研究，其中直方图均衡及其改进算法和Retinex算法及其改进算法应用较为广泛［6］。典型代表有直方图均衡化（Histogram Equalization，HE）、自适应直方图均衡化（Adaptive Histogram Equalization，AHE）［7］、Retinex算 法［8］、单尺度Retinex算法（Single-Scale Retinex，SSR）、多尺度Retinex算法（Multi-Scale Retinex，MSR）［9］等。然而直方图均衡及其改进算法往往需要根据不同场景人为调整参数，并且参数的选取对图像处理效果影响较大，导致对比度增强效果稳定性较差，增强结果不易控制［10］。而Retinex及其改进算法大多为全局增强处理。中子照相成像系统由于存在中子辐射干扰，成像结果往往嵌入大量低频背景和噪声信号中［11］，全局增强易将背景噪声同时放大，导致图像增强效果不佳，甚至会引发图像质量倒退的现象。因此局部自适应对比度增强算法更适合中子图像对比度增强，可以避免大量低频背景噪声对提升过程的干扰，此外为了提升处理效果的稳定性需要采用优化算法求解参数值来代替人工设定的参数值。

针对中子图像特点和对比度优化需求，本文选取自适应对比度增强算法（Adaptive Contrast Enhancement，ACE）对中子图像进行对比度优化，这种算法可以有效缓解低频背景的干扰。另外为了解决现有对比度增强算法在提升过程中的不稳定性问题，本文将群智能技术与自适应对比度增强技术相结合，采用基于粒子群优化的自适应对比度增强算法，找到全局最优增益因子系数，利用全局最优增益因子系数对中子图像进行局部自适应对比度增强。本文算法可以还原图像细节，提高图像对比度，有效提高了中子照相图像质量，且通过粒子群寻优算法根据图像本身特点设置最优参数值，避免了经验值参数给处理效果带来的影响，增强了算法处理效果的稳定性。

1 相关算法

1.1 自适应对比度增强算法

自适应对比度增强（Adaptive Contrast Enhancement，ACE）算法［12］通过结合图像自身特点，对本身对比度很强的图像区域进行较小比例增强，对本身对比度弱的图像区域较大幅度增强。算法基本原理是将图像分成两部分：低频部分和高频部分，低频部分可通过均值滤波求解得到，高频部分可通过原图与低频部分做差得到。利用增益因子实现对图像高频部分的增强和放大，从而达到自适应调节的目的，整体过程如下：

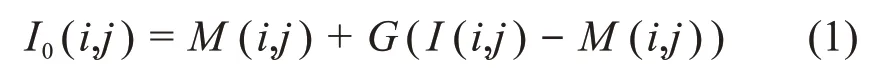
式中：M(i，j)为以像素点(i，j)为中心的局部均值；I(i，j)为像素点(i，j)对应的初始像素值；G为增益系数；I0(i，j)为结果图像中像素点(i，j)对应的像素值。

由于标准差表示的是图像像素均匀性，局部区域标准差越大，则表明其像素值越不均匀，对比度越强，反之标准差越小，其像素值越均匀，对比度越弱。所以将标准差作为增益因子G的动态取值计算参数之一，如式（2）：

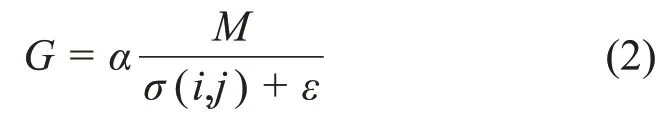
式中：M为全局均值；σ(i，j)为以像素点(i，j)为中心的局部标准差；α为增益因子系数，选取（0，1）任意固定值；ε为极小正常数项，用于避免因出现局部标准差为零而导致的公式计算错误（本文ε=10-7）。

由式（2）可以看出，自适应对比度增强算法中增益因子的计算需要一个增益因子系数α调节高频部分的增益程度，通常增益因子系数α往往选取一个固定经验值，但是这样就会给增强过程带来不稳定性，因此对于自适应对比度增强算法有必要选取一个最优增益因子系数α，以便能够保证最佳的对比度提升效果。

1.2 粒子群优化算法

粒子群优化算法（Particle Swarm Optimization，PSO）［13］由Kennedy和Eberhart提出，模拟鸟群在觅食过程中的集群行为而设计。相比于遗传算法，它省去了复杂的“交叉”、“变异”等过程，PSO算法从随机解出发，通过不断迭代的过程在解空间中搜索最优解。其核心思想延续了智能优化算法，即通过群体中个体之间的协作和信息共享来寻找最优解。

PSO算法［14］通过设计一种无质量粒子模拟觅食鸟群中的鸟，这种无质量粒子具有两个属性：速度和位置。速度代表粒子移动的快慢，位置代表粒子移动的方向。每个无质量粒子在搜索空间中单独寻找最优解，记为当前个体最优解（pbest），和整个粒子群中的其他粒子共享这个个体最优解，整个粒子群中最优的个体值视为当前全局最优解（gbest）。粒子群中的所有粒子根据当前找到的个体最优解和整个粒子群共享的当前全局最优解不断迭代更新自己的速度和位置，最终所有粒子都收敛于最优解周围，从而实现最优化。

由于PSO算法简洁，易于实现，且在非线性连续、组合和混合整数非线性等优化问题上具有较好性能，目前已经在函数优化、神经网络训练、模糊系统控制以及其他遗传算法等领域有着非常广泛的应用［15］。考虑到PSO算法在函数优化方面的优势，本文选取该算法用于自适应对比度增强算法的增益因子系数α的寻优。

2 改进的自适应对比度增强算法

本文算法主要为按照自适应对比度增强算法（ACE）思想将图像分成高频部分和低频部分，对于代表细节的高频部分进行增益计算。以图像信息熵和标准差作为目标函数，通过粒子群优化算法（PSO）迭代优化找到图像的最优增益因子系数，将所求解的全局最优增益因子系数代入ACE算法中进行局部自适应对比度增强，克服了ACE算法采用固定系数值增益所导致的处理效果不稳定，对中子图像进行了自适应的对比度增强，减小了大量暗区对中子检测的干扰，还原图像细节，提高图像质量。本文算法基本流程如图1所示。

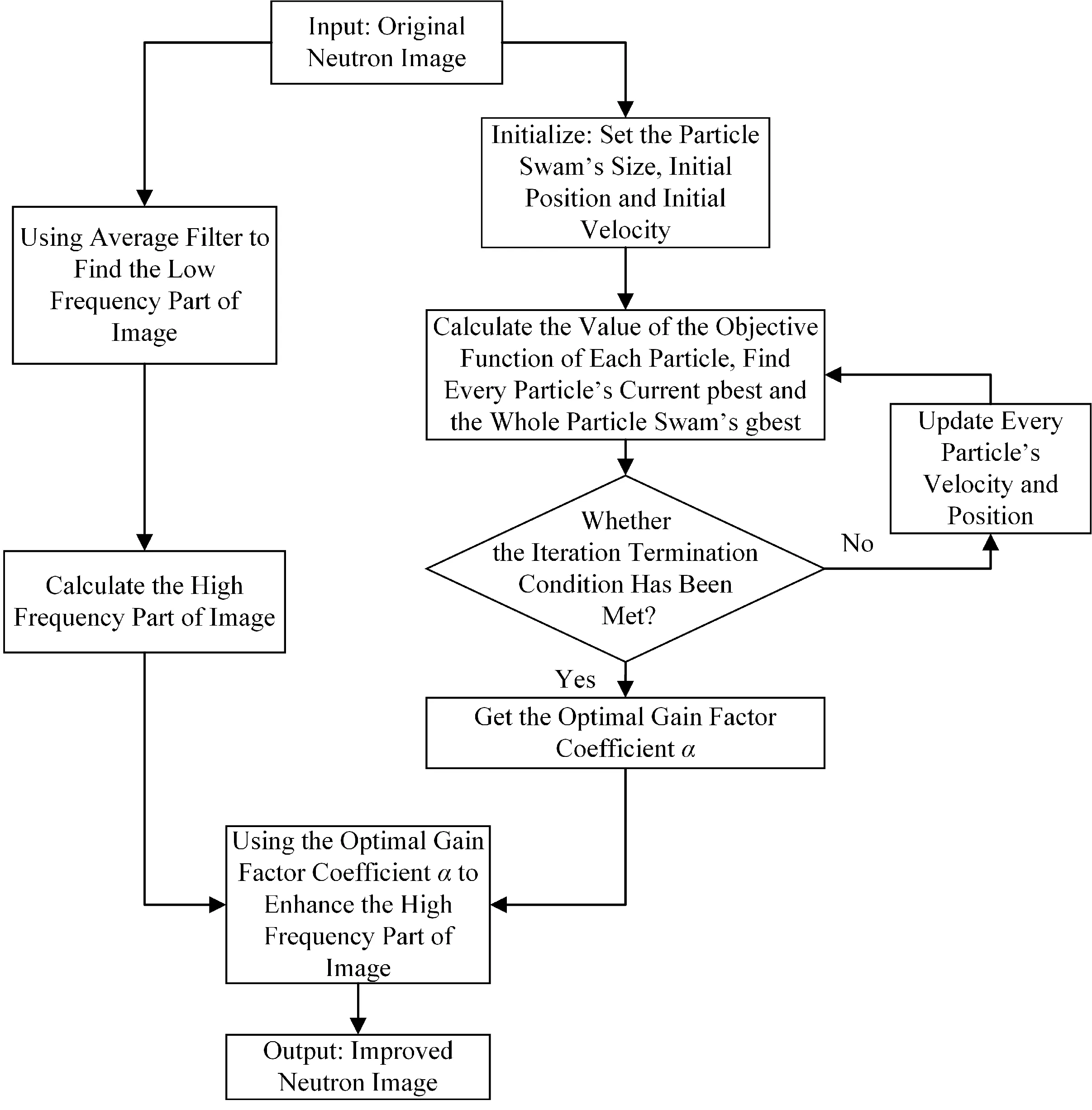
图1 算法基本流程图Fig.1 The flow chart of algorithm

2.1 增益因子系数寻优过程

为解决固定系数带来的不稳定性，本文采用PSO算法寻找增益因子系数α的最优解，将增益因子系数看作粒子，首先初始化一个固定大小的粒子群（本算法中构造了一个含有24个粒子的粒子群），并对粒子群中的每一个粒子进行速度和位置的随机初始化，粒子在每一次迭代中都会根据目标函数评估出每个粒子的适应度值（fitness），若fitness是粒子的当前个体最优解，则将它存储为pbest，若fitness是当前粒子群中的全局最优解，则将它存储为gbest，然后根据pbest和gbest对各粒子进行位置和速度的更新，更新公式如式（3）和式（4）所示：

式中：i表示当前粒子；t表示迭代次数；表示第i个粒子在第t次迭代时的速度；xti表示第i个粒子在第t次迭代时的位置。C1、C2为加速常数，前者为每个粒子的个体学习因子，后者为每个粒子的社会学习因子，通常令C1=C2=2，可以在不易陷入局部最优的前提下加快收敛。表示第i个粒子在第t次迭代时的个体最优解，表示第i个粒子在第t次迭代时的全局最优解。

式（3）中ω为惯性因子，用来衡量全局寻优性能和局部寻优性能。当ω较大时，全局寻优能力较强，局部寻优能力较弱。考虑到在迭代早期较大的ω有助于粒子群的全局快速收敛，而迭代后期粒子群已经较集中于最优范围内，此时应通过较小的ω增强局部搜索能力，在最优范围内更加精细地搜索最优解。因此采用线性递减法自适应地选择ω，其计算公式如式（5）所示：

式中：ωmax和ωmin分别为惯性权重最大值和最小值；tmax为最大迭代次数。

通过不断地迭代和更新，当满足迭代终止条件（迭代次数达到最大迭代次数tmax）时各粒子收敛于最优值附近，即增益因子系数获得了最优解。

2.2 选择评价函数

在对增益因子系数进行粒子群优化的过程中，评价函数的选择是至关重要的，每个粒子根据评价函数评估所得到的适应值fitness是评价中子图像增强效果的重要标准。中子图像由于其中子源和成像系统的限制，导致图像分辨率较差，存在大量暗区，细节丢失严重。因此要求对比度增强后的中子图像应具有信息量大、对比度高等特点［16］。在本文算法中，将灰度标准方差和图像信息熵融入评价函数中，作为每个粒子的寻优目标函数，其评价函数如式（6）所示：

式中：α1和α2分别表示信息熵和标准差在评估中所占比例，此处α1和α2均等于1/2，表示H和Std占比相同。

H代表图像信息熵，在图像中，图像的熵代表整张图像的不确定性，可以用图像熵来衡量图像所包含信息量的大小，也可以表示图像灰度值分布的聚集特征，熵越大则图像中的灰度值在一定范围内越均衡，表现在视觉上就是图像对比度越大，图像质量越高，计算过程如式（7）所示：

其中：pn表示图像中灰度值n所占比例。

Std代表图像标准差，标准差表示的是图像的像素值的均匀性，可以认为标准差越大的局部区域，其像素值越不均匀，对比度越强；反之，标准差越小的局部区域，其像素值越均匀，对比度越弱。

通过从信息熵和标准差两个维度对粒子进行评估，将多目标函数线性排列来解决多目标优化的问题，从而使选取的增益因子系数能够最大化保证图像信息量和像素均匀性，满足增强中子图像细节，提高中子图像对比度的要求。

2.3 改进算法过程

改进的自适应对比度增强优化算法具体过程为：

1）输入原始中子图像。

2）将增益因子系数α看作粒子，初始化增益因子系数的种群和参数。包括种群个数N、粒子位置x和速度v；惯性权重最大值最小值ωmax和ωmin；学习因子C1和C2、最大迭代次数tmax等。

3）评价每个增益因子系数α。分别计算熵值H、计算灰度标准方差Std，得到每个增益因子系数的适应度值（fitness）。

4）更新增益因子系数最优值。如果更新后的适应度值大于原来个体最优值pbest，则将该增益因子系数位置作为当前个体最优值pbest，如果更新后增益因子系数适应度值大于原来全局最优值gbest，则将该增益因子系数位置作为当前全局最值优gbest。

5）判断是否达到迭代停止条件（即达到迭代次数tmax），若未达到，则更新每个增益因子系数的速度与位置，跳转到3）。若满足迭代停止条件，退出循环。

6）使用迭代中存储下来的最优增益因子系数α（gbest）对图像进行ACE算法增强处理。

7）输出经算法处理之后的中子图像。

3 结果与分析

为了验证新算法的实际效果，本文对多幅中子照相成像图片进行优化测试。其中图2和图3分别为来自德国慕尼黑工业大学FRM-II实验堆的钟表样品和涡轮叶片样品中子照相图像，图4为基于HINEG加速器中子源获取的线对样品和阶梯样品的快中子照相图像，图5为中国原子能研究院先进堆中子照相装置获取的汽车火花塞中子照相图像。将本文算法优化结果分别与原图、MSR算法和传统ACE算法优化结果进行效果对比，并计算给出了信息熵、灰度平均梯度和图像对比度三项客观评价参数结果。

3.1 效果对比

不同算法对于钟模型中子图像的增强效果如图2所示。可以看出原始图像存在大量暗区，样品细节模糊不清。图2（b）存在由于图像整体同尺度提升而导致的对比度提升不均匀的现象。图2（c）虽然细节处较为清晰但存在严重的噪声放大现象。采用本文算法对原始图像数据处理之后的结果，在提高对比度的同时齿轮细节处也得到了很好的保持，具有局部自适应性，对比度均匀。迭代优化过程中，最优增益因子系数α对应的目标函数值随迭代次数更新的曲线图（见下文图6（a）），函数值在大约第25次迭代时收敛于最优值附近（α=0.000 102 419，fitness=2.255 52）。

图2 钟表样品中子成像原始图(a)、MSR算法处理图(b)、ACE算法处理图(c)和本文算法处理图(d)Fig.2 Neutron radiography of clock sample's original image(a),image processed by MSR algorithm(b),image processed by ACE algorithm(c)and image processed by improved adaptive contrast enhancement algorithm(d)

涡轮叶片中子图像用不同算法增强后效果如图3所示，可以看出原始图像中冷却通道和边缘小孔处较暗，图3（b）对比度略有提高但图像对比度不均匀，图3（c）对比度提升效果不明显。图3（d）表明本文算法对涡轮叶片中子图像进行处理后，更容易看清叶片的边缘小孔和冷却通道，对比度得到了较好的增强。迭代曲线（见下文图6（b））表明其函数值在大约第70次迭代时函数值收敛于最优值附近（α=0.000 509 162，fitness=2.252 34）。

图3 涡轮叶片中子成像原始图(a)、MSR算法处理图(b)、ACE算法处理图(c)和本文算法处理图(d)Fig.3 Neutron radiography of turbine plate's original image(a),image processed by MSR algorithm(b),image processed by ACE algorithm(c)and image processed by improved adaptive contrast enhancement algorithm(d)

图4给出了不同算法在线对、阶梯样品中子图像上的效果对比。原始图像中样品信息嵌入在大量低频背景信号中，图像整体较暗，对比度差，不利于对样品的分析。图4（b）所示MSR算法使原始图像对比度小幅提升，但由于是全局增强，没有突出样品细节。图4（c）虽在细节处提高了样品分辨率，但整体对比度仍不足。本文算法对样品细节和图像整体的对比度均有明显提升，肉眼更容易识别线对样品中不同间隔的明暗线对信息以及阶梯样品的灰度渐变信息。迭代曲线（见下文图6（c）表明，大约在第60次迭代时函数值收敛于最优值附近（α=0.072 763，fitness=2.263 52）。

图4 线对、阶梯样品中子成像原始图(a)、MSR算法处理图(b)、ACE算法处理图(c)和本文算法处理图(d)Fig.4 Neutron radiography of lines and ladder samples'original image(a),image processed by MSR algorithm(b),image processed by ACE algorithm(c)and image processed by improved adaptive contrast enhancement algorithm(d)

图5为汽车火花塞中子图像通过不同算法增强之后的效果对比图，可以看出原图中螺旋条纹细节不清晰，图5（b）所示MSR算法虽提高了火花塞中子图像整体对比度，但细节部分并没有得到突出显示。相比于图5（b），图5（c）细节处清晰度略有提升。本文算法提高了火花塞中子图像的整体和局部对比度，尤其是火花塞底部细节得到了较大程度还原。整个寻优过程的迭代曲线，大约在90次迭代时函数值收敛于最优值附近（α=0.846 859，fitness=2.236 8）。图2～图5样品迭代寻优曲线结果如图6。

图5 汽车火花塞中子成像原始图(a)、MSR算法处理图(b)、ACE算法处理图(c)和本文算法处理图(d)Fig.5 Neutron radiography of sparkplug's original image(a),image processed by MSR algorithm(b),image processed by ACE algorithm(c)and image processed by improved adaptive contrast enhancement algorithm(d)

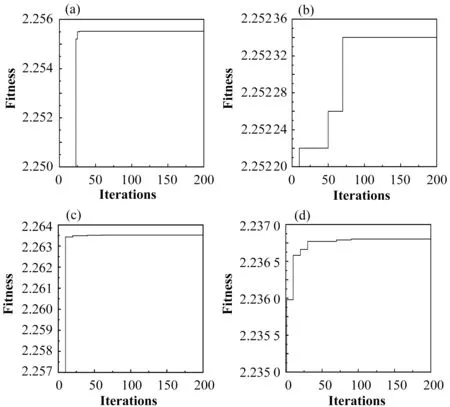
图6 最优目标函数值随迭代次数更新曲线图(a)图2，(b)图3，(c)图4，(d)图5Fig.6 The optimal objective function value updates with the number of iterations(a)Fig.2,(b)Fig.3,(c)Fig.4,(d)Fig.5

3.2 评价参数对比

3.2.1 图像信息熵

由前文可知，图像信息熵可以衡量图像信息量的多少，因此本文根据式（7）计算得到图像信息熵数值，用来评价测试图像处理效果［17］。表1为测试图像2、图像3、图像4和图像5的熵值比较，可以看出本文算法对于4幅图像的信息熵值均有明显提升，表明本文算法可以还原图像细节，提高图像质量。

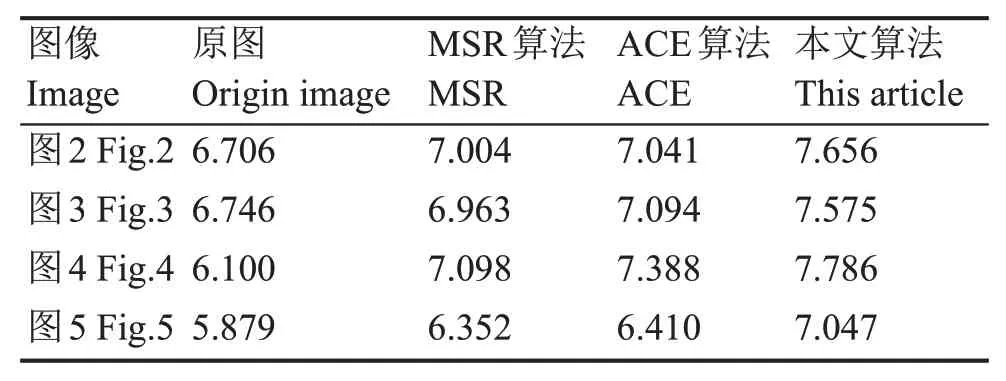
表1 测试图2～图5的熵值比较Table 1 Comparison of Fig.2～Fig.5's entropy value

3.2.2 灰度平均梯度

灰度平均梯度(Grayscale Mean Gradient,GMG)［18］指图像的边缘细节或影线两侧附近有明显差异的灰度值，可以反映图像细微处反差变化的速率，即灰度变化率。这种灰度变化率的大小可用来表征图像的相对清晰度。平均梯度越大，图像层次越多，图像细节越清晰。计算公式如式（8）所示：

由表2可以看出，本文算法对于4幅图像的灰度平均梯度均有明显提升，表明经过本文算法处理后图像清晰度提高。

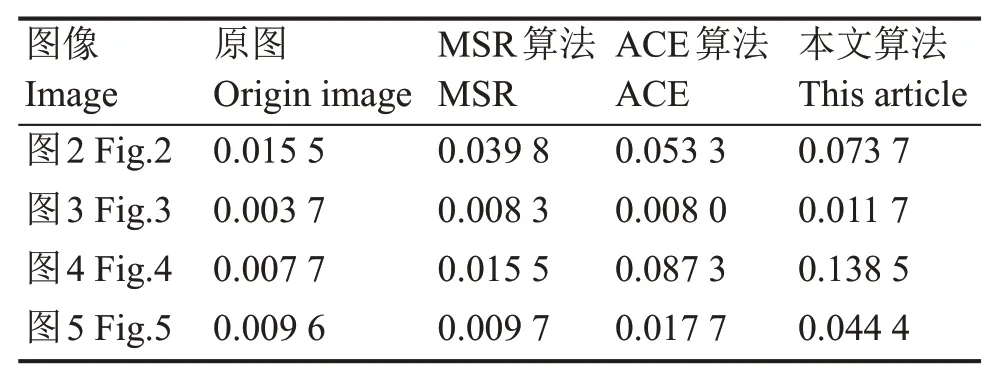
表2 测试图2～图5的GMG值比较Table 2 Comparison of Fig.2～Fig.5's GMG value

3.2.3 图像对比度

对比度计算［19］是衡量图像对比度性能的最直观和最基本的重要指标，对比度数值越高，说明图像对比度越好，展示的细节就越丰富，其计算公式如式（9）所示：

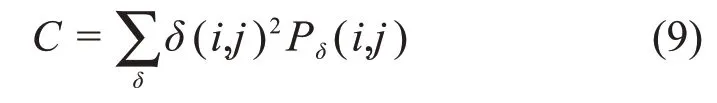
式中：δ(i，j)为滤波窗口内相邻像素之间的灰度差值（本文中求取对比度的滤波窗口大小取3×3），Pδ(i，j)为相邻像素间灰度差为δ的像素分布概率。计算结果如表3所示，通过对多幅图像、不同算法的对比度数值对比，证明了本文算法在对比度提升方面的有效性。

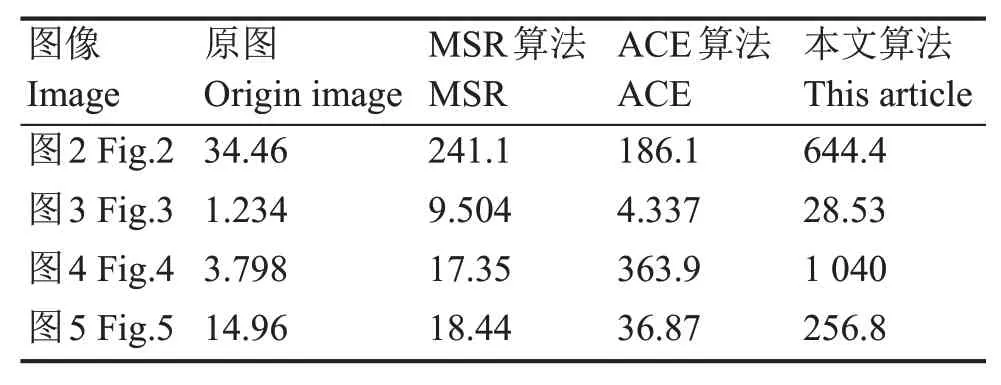
表3 测试图2～图5的对比度比较Table 3 Comparison of Fig.2～Fig.5's contrast value

3.3 自适应对比度增强算法中窗口选值分析

自适应对比度增强算法中窗口大小的取值可能会对图像增强效果带来影响，窗口内每个像素值与其均值相似，式（1）中I(i，j)-M(i，j)很小，因此对图像增益效果不是很好，而当窗口较大时，在较大图像块内式（1）中M(i，j)相同，图像块内得到的新像素值较为接近，因此边缘和细节部分增强效果略差，易发生局部模糊。为证明窗口大小设置为7×7的有效性，本文对图2～图5在滤波窗口尺寸大小分别设置为3、5、7、9、11时运用本文算法增强后图像的信息熵值、GMG值和对比度值进行了对比分析，结果分别如图7的（a）、（b）、（c）所示，可知当窗口大小取7×7时，能够更好地兼顾整体和局部的处理效果，其各项评价指标计算总体优于其他窗口大小对应数值。因此本文选取7×7作为自适应对比度增强算法局部处理过程中的窗口尺寸。

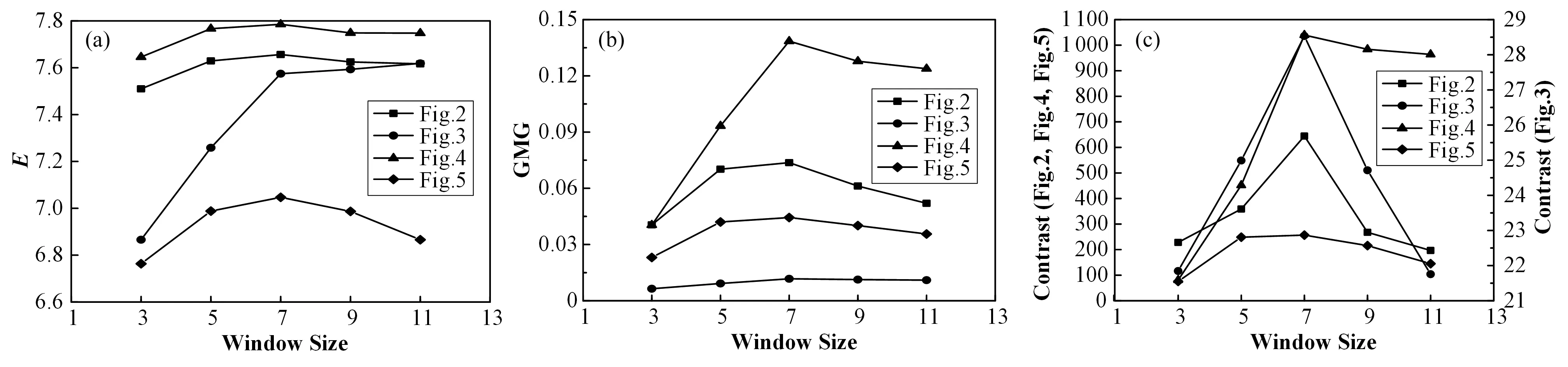
图7 4幅图像取不同窗口大小时对应的信息熵值(a)、GMG值(b)和对比度值(c)Fig.7 The entropy value(a),GMG value(b)and contrast value(c)corresponding to different window sizes of the four images

4 结语

本文提出了一种基于粒子群优化的自适应对比度增强算法，并将该算法运用到中子图像上进行分析。通过图像处理之后的效果和指标的对比，可以得出以下结论：

1）新算法采用粒子群优化算法获取最优增益因子系数α，从图像本身获取算法参数，再进行局部自适应的图像对比度优化，图像处理具有较好的稳定性。

2）与传统的MSR算法、ACE算法相比，新算法在提高中子照相图像对比度方面具有一定优势，其处理图像的信息熵、灰度平均梯度和对比度参数均更为优异。

基于上述研究结果，新算法在中子照相图像处理领域具有明确的应用前景，并已开始广泛应用于本单位基于加速器中子源的中子照相图像优化。由于该算法采用粒子群优化算法获取最优增益因子系数α的过程需要多次迭代耗时较长，算法目前还无法满足中子CT或动态成像等高速多帧图像实时处理需求，下一代的高速对比度优化算法目前正在开发中。

致谢感谢中国原子能科学研究院物理所中子散射团队及德国慕尼黑工业大学Burkhard Schillinger教授提供了相关中子照相图像用于本文算法测试。