不同吸气策略对风力机翼型动态失速特性的影响
2021-07-17陈微圣孙晓晶
陈微圣,孙晓晶
(1.上海理工大学 能源与动力工程学院,上海 200093; 2.上海市动力工程多相流动与传热重点实验室,上海 200093)
动态失速的主要特征是翼型上表面产生大尺度分离涡和非线性的迟滞失速现象[1],失速涡的形成和脱落会产生很大的阻力和俯仰力矩,导致风力机叶片颤振、气动效率骤降和高速运行范围急剧减小等问题[2-3]。余海洋等[4]以S809翼型为研究对象,考虑在吸力面放置回流襟翼来控制其动态失速。Tadjfar等[5]采用数值模拟方法研究了雷诺数为106时表面带射流的NACA0012翼型的动态失速特性。Xu等[6]将联合射流运用到NREL S809翼型的动态失速控制上,发现较高的动量系数可完全抑制分离。李宇红等[7-8]发现在距离前缘5%c~10%c(c为弦长)处进行吸气控制可有效提高翼型的静态气动性能。Karim等[9]发现表面吸气可有效抑制翼型吸力面上动态失速涡的产生和发展。Rezaeiha等[10]在单翼型垂直轴风力机翼型下表面添加吸气口,结果发现吸气口沿层流分离泡的弦向延伸可有效抑制气动载荷的波动。Sun等[11]通过数值模拟的方法在三叶片垂直轴风力机上下表面施加吸气控制,在考虑吸气能耗的情况下,翼型各迎角均存在最优吸气动量。
在高雷诺数下,笔者采用非定常雷诺平均方法(RANS)对NACA0012翼型在振荡条件下的动态失速进行了数值模拟,分析了表面吸气控制对翼型动态失速特性的影响。此外,研究了采用不同控制方法时翼型气动力系数迟滞环的变化趋势,并结合能耗得到最佳吸气策略。
1 数值方法
1.1 运动方程
翼型绕其气动中心(距前缘0.25c处)在5°~25°之间进行俯仰运动,瞬时攻角a可表示为:
a=a0+Asin(2πft)
(1)
式中:a0为平均攻角,取15°;A为振荡幅度,取10°;f为频率;t为时间。
k=πfc/V∞
(2)
式中:k为折合频率,取0.15;V∞为来流速度。
1.2 计算域的划分
利用软件Pointwise V18进行网格划分。如图1所示,以NACA0012翼型上下表面为起始线,且保证y+≈1,向外拓半径为5c的O型结构化网格,以确保网格具有较好的正交性。旋转域的外围同样采用结构化网格,半径为70c。边界条件设置如下:来流进口和吸气口分别设为速度进、出口边界,吸气方向垂直于壁面[12],来流出口设为压力出口边界,翼型壁面设为无滑移壁面。计算采用滑移网格技术[13],压力-速度耦合采用Simple算法,对压力和动量进行二阶空间离散。
在翼型吸力面上距前缘12%c位置开设宽度d为1%c的吸气口,吸气动量系数分别取0.002和0.02,其中动量系数Cμ为:
(3)
式中:qm,s为吸气口质量流量;Vs为吸气口速度;S为翼型面积,在二维中为弦长;ρ为流体密度。

(a) 带吸气的翼型模型



(b) 翼型计算域及局部网格
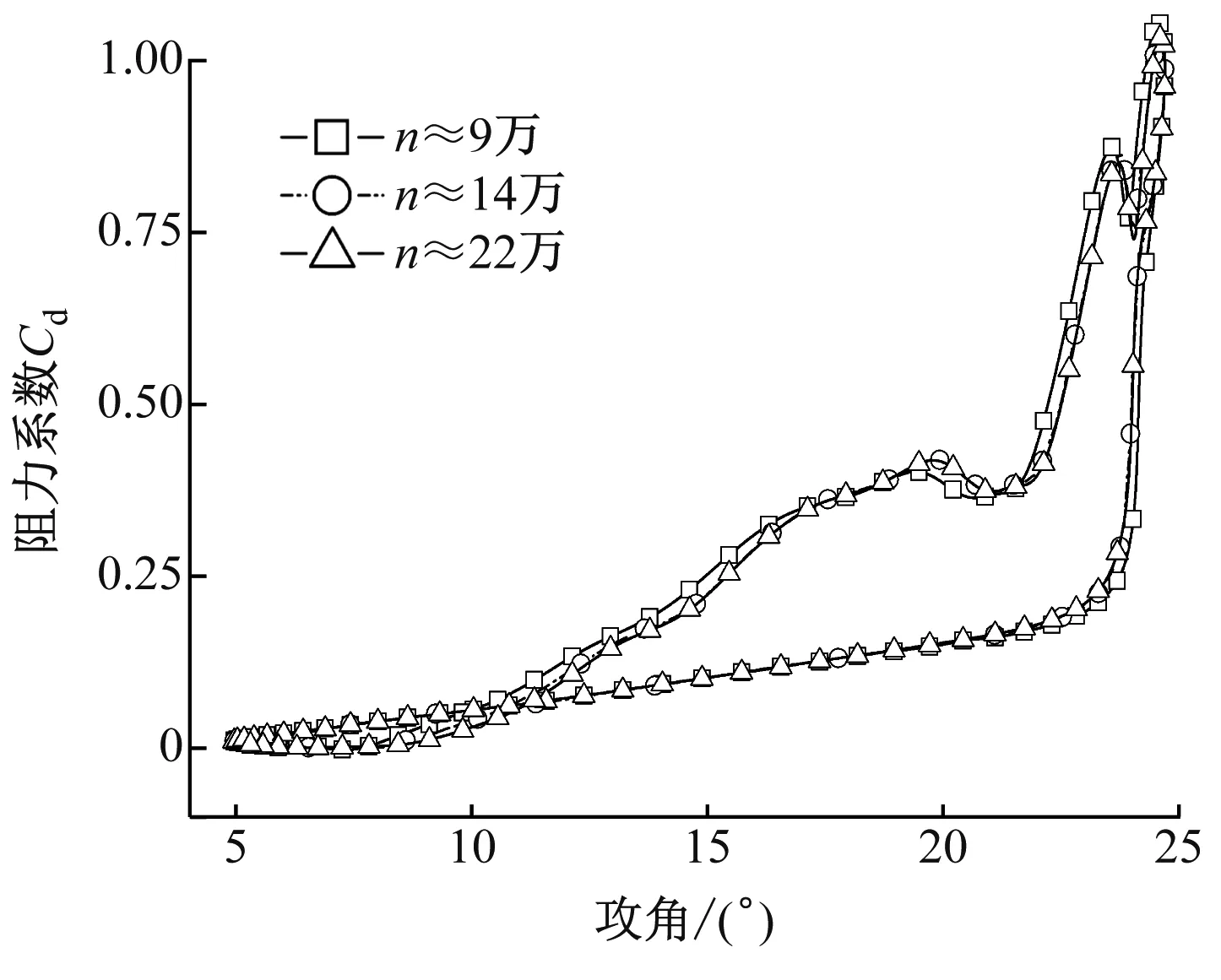
1.3 网格无关性验证
为了验证最终网格的准确性,选取不同网格数进行无关性验证,如图2所示。当网格数n约为14万和22万时,升力系数和阻力系数曲线均明显贴合,而网格数约为9万和14万时,升力系数和阻力系数计算结果均有微小差别。因此,选取网格数约为14万。
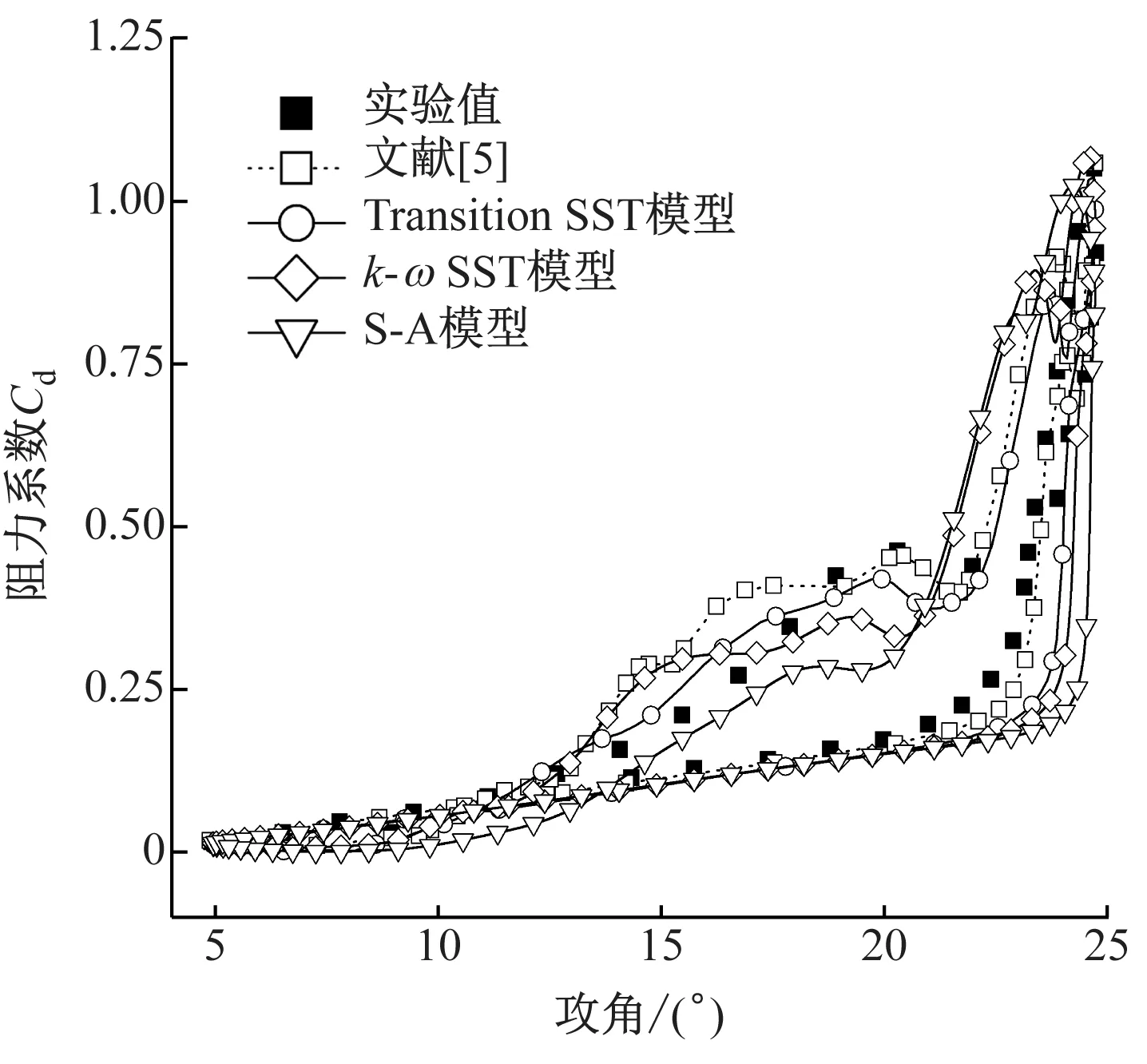
1.4 模型可靠性验证
选用Transition SST、k-ωSST和S-A 3种模拟翼型气动性能的模型,并将各模型计算得到的升力系数、阻力系数与实验值[14]和文献[5]中的模拟值进行对比,结果见图3。由图3(a)可以看出,在翼型上仰过程中不同模型的升力系数模拟值与实验值均相差不大,且在23.5°左右升力系数出现骤升,而在下俯运动中不同模型的升力系数模拟值走向有差别。如图3(b)所示,与其他模型相比,Transition SST模型得到的阻力系数模拟值与实验值更接近。总体上看,Transition SST模型能更好地预测出翼型升力系数和阻力系数的变化趋势,因此采用Transition SST模型来进行数值模拟。
2 吸气和喷气控制对动态失速的影响
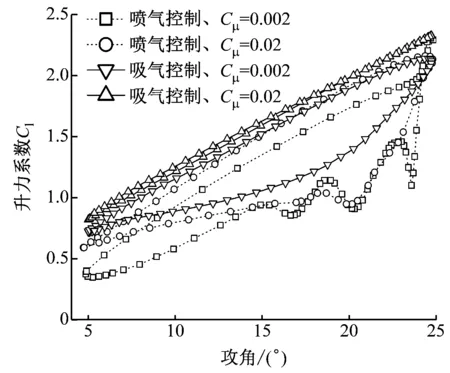
笔者研究了吸气和喷气控制对动态失速的影响,其中喷气数据对应文献[5]中最佳喷气位置(4%c)。如图4所示,在不同动量系数下吸气控制较喷气控制具有更显著的增升减阻效果。当动量系数为0.002,采用吸气控制时平均升力系数较喷气控制提高13.85%,阻力系数降低80%;当动量系数为0.02,采用吸气控制时升力系数迟滞环收缩成与攻角呈线性关系,阻力系数也进一步降低;采用喷气控制时,与动量系数为0.002相比,动量系数为0.02时升力系数和阻力系数均有所改善,且与吸气控制下动量系数为0.002时的迟滞环接近。

(a) 升力系数
(b) 阻力系数
图5为NACA0012翼型在俯仰运动过程中的速度流线图。上仰攻角为22.93°时翼型尾缘发生分离,产生尾缘涡1;随着攻角的增大,该涡向上游迅速扩散,并在24.25°上仰攻角下形成前缘涡2;攻角增至最大(25°)时,前缘涡2沿弦向流动,诱发二次涡3的产生。当下俯攻角为24.35°时,前缘涡2与尾缘涡1融合形成主分离涡2,此时前缘涡2面积达到最大。当下俯攻角为22.88°时,主分离涡2一部分脱落,另一部分驻留在尾缘,直到下俯到攻角为20.49°才完全脱落。由图5(g)和图5(h)可知,随着下俯攻角的减小,二次涡3逐步增大并脱离壁面。

(a) 升力系数
(b) 阻力系数
(a) 升力系数

(b) 阻力系数

(a) 上仰攻角为22.93°

(b) 上仰攻角为24.25°
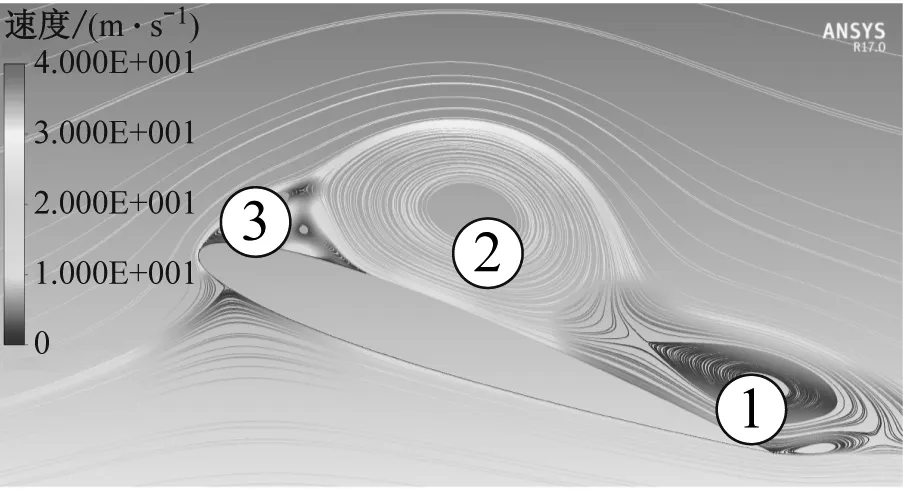
(c) 攻角为25°

(d) 下俯攻角为24.35°

(e) 下俯攻角为22.88°

(f) 下俯攻角为20.49°
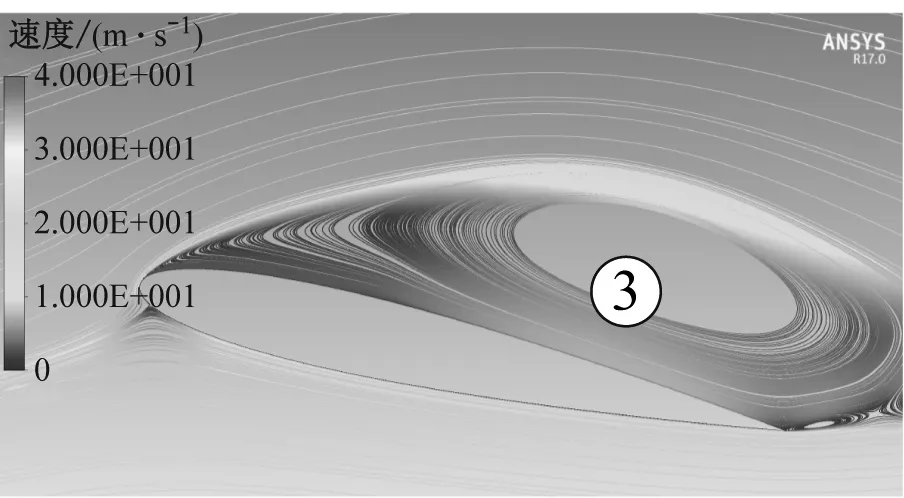
(g) 下俯攻角为17.44°

(h) 下俯攻角为12.03°
在相应动量系数下带吸气和喷气控制时翼型周围的涡云图分别见图6和图7。当动量系数为0.02时,采用吸气控制可完全抑制翼型整个周期俯仰运动产生的失速涡,仅在尾缘存在很短的剪切层。在动量系数为0.02(喷气控制)以及动量系数为0.002(吸气控制)的情况下,上仰过程中喷气与吸气的控制效果在15°和23°攻角下均几乎一致,其原因主要是在攻角23°下才产生动态失速涡。攻角为25°时,在翼型吸力面上采用喷气控制较吸气控制具有更厚的剪切层。当下俯到攻角为23°时,在动量系数为0.02(喷气控制)以及动量系数为0.002(吸气控制)的情况下流体分别在吸力面距前缘c/4和c/3处分离,且前者产生了较大的负涡区和尾缘涡,导致下俯过程整体升力系数要低于后者。综上,动量系数较小且采用吸气控制时平均升力系数较喷气控制高7%,平均阻力系数低40%;吸气控制消耗更少的能量就能够抑制前缘涡的产生,使流体更好地附着在翼型表面。

图6 上仰过程中带喷气和吸气翼型周围的涡云图对比
Fig.6 Comparison of vortex cloud patterns around the airfoil with jet and suction control during the uppitch process

图7 下俯过程中带喷气和吸气翼型周围的涡云图对比
Fig.7 Comparison of vortex cloud patterns around the airfoil with jet and suction control during the downward process
不同时刻下NACA0012翼型和采用吸气、喷气控制时翼型的压力系数分布见图8。由图8可知,采用吸气和喷气控制均会使翼型前缘吸力峰有较强的低压区,曲线畸变均发生在射流和吸气口所在位置。在25°攻角下,采用吸气控制、动量系数为0.002和0.02时翼型吸力面压力系数峰值分别为-21.5和-22.5,较喷气控制分别低1.5和2.5,而带吸气与喷气控制的翼型表面其他位置的压力系数均较接近。2种控制会使翼型前缘附近区域上下表面产生很大的压差,但对翼型下游段压力的影响较小,因此翼型前缘对增升减阻的贡献要大于尾缘。下俯攻角为23°时,NACA0012翼型在尾缘出现较大的压差,这是由尾缘涡脱落造成的。此时,在2种控制下压力系数曲线差别较大,与喷气控制相比,采用吸气控制时在翼型前缘吸力面与压力面之间的压差更大,而尾缘的压差更小。采用吸气控制时,随着动量系数的增加,翼型吸力面压力系数峰值降低约3.5,尾缘压差进一步减小。2种控制下翼型在尾缘压差的显著区别说明吸气控制比喷气控制能更好地抑制涡脱落。

(a) 攻角为25°
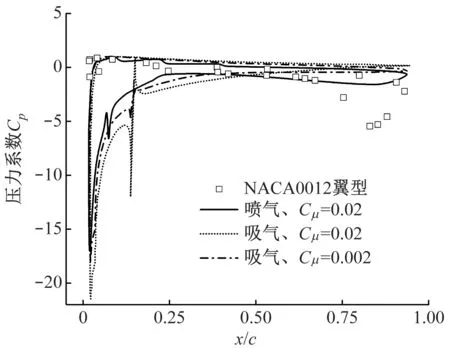
(b) 下俯攻角为23°
3 不同吸气策略
如图9所示,针对带吸气翼型设计了4种控制吸气动量的函数,包括分段函数、开口向下Sin函数、开口向下一次函数和定常函数,0~0.5T(T为周期)为翼型上仰阶段,0.5T~1T为翼型下俯阶段。
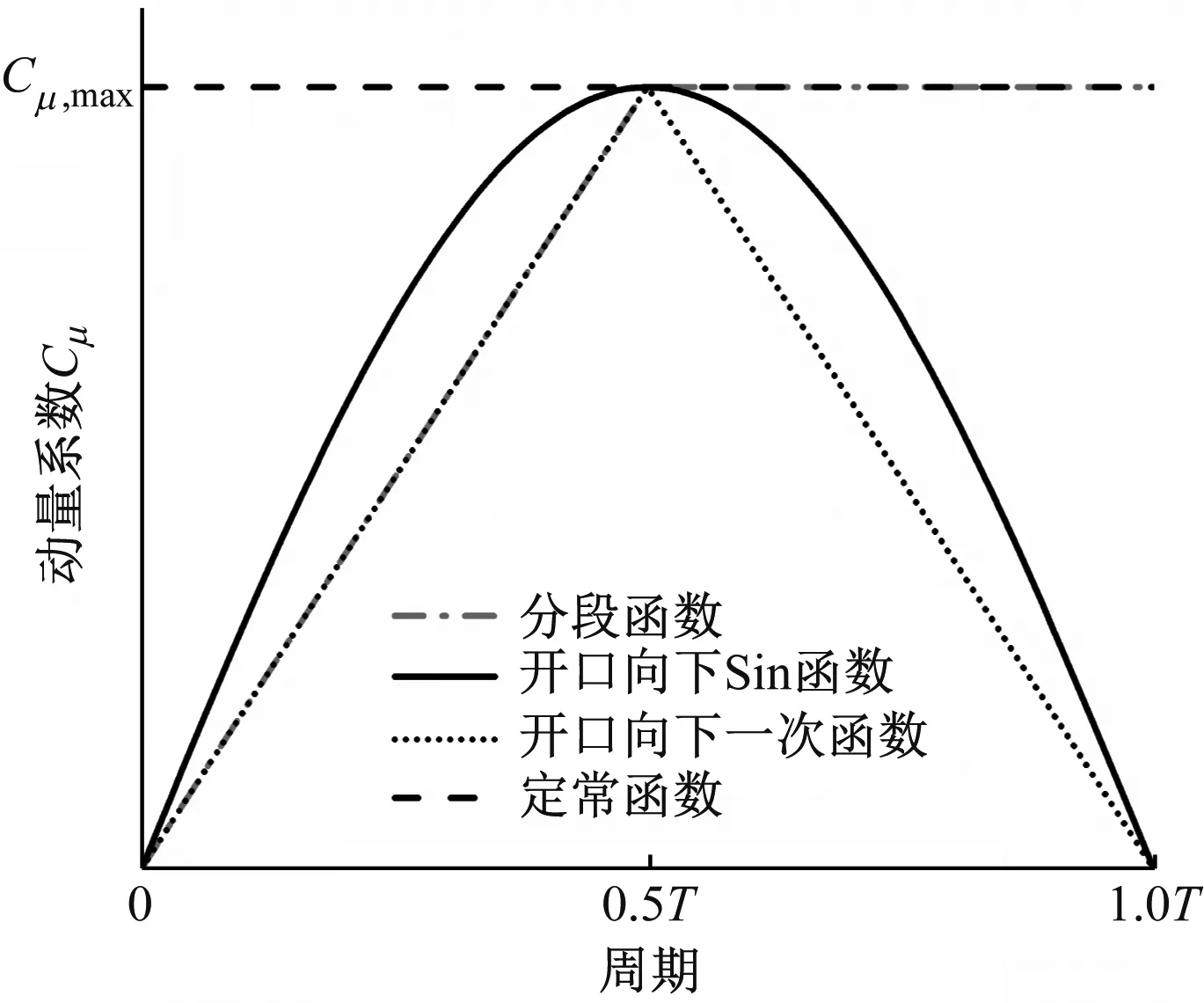
图9 4种吸气策略的函数曲线
图10给出了不同最大动量系数下NACA0012翼型与施加4种吸气策略翼型的非定常气动力系数对比。当最大动量系数Cμ,max=0.002时,采用吸气控制的翼型升力系数较NACA0012翼型更大,阻力系数减小,俯仰力矩峰值降幅超过80%。在分段函数策略下,气动力系数的迟滞环与定常函数策略较为贴合,而采用开口向下Sin函数和开口向下一次函数策略时翼型下俯阶段阻力系数下降不明显,在16°攻角下升力系数均显著下降。与其他吸气策略相比,采用开口向下Sin函数策略时在上仰过程中整体升力系数最大。随着动量系数从0.002增大至0.02,不同吸气策略下的升力系数均明显增大,迟滞环面积几乎为0,4种吸气策略下的阻力系数和俯仰力矩系数曲线几乎重合,翼型俯仰过程的动态失速能得到有效抑制。可见,在不同吸气策略下,翼型气动力系数的差异性随吸气速度的增大而减小,因此耗能的大小成为判断各吸气策略优劣的关键指标。
图11给出了不同最大动量系数和攻角时采用4种吸气策略的速度流线图。采用开口向下一次函数策略时翼型尾缘涡结构最强,其次分别是开口向下Sin函数、定常函数和分段函数。结合图10可知,最大动量系数为0.002、下俯攻角为17.44°时升力系数随着涡结构的变大而提高,阻力系数随着涡结构的变小而降低,该涡结构具有增升增阻的作用。最大动量系数为0.02、攻角为25°时,在不同吸气策略下翼型表面的分离流体附着在吸力面,动态失速涡完全消失,各速度流线的控制效果几乎一致。
循环控制技术需消耗能量产生吸力,Tongchitpakdee等[15]提出射流功率与射流质量流量和射流单位质量动能成正比。吸气耗能系数Pc为:
(4)
式中:ρs为吸气流体的密度;As为吸气口面积,二维模拟中取吸气口宽度;Vs为吸气速度;ρ∞为来流密度。
升阻比是衡量风力机气动性能的重要指标之一,Sun等[11]提出修正后的等效升阻比(Cl/Cd)c可表示为:
(5)
该式将吸气的耗能视为阻力的一种表现形式[16],本文也进行类似研究。
最大动量系数为0.02时翼型的动态失速可完全被抑制,故讨论该条件下采用4种吸气策略时耗能系数和等效升阻比的情况,计算结果见图12。由图12可知,在开口向下一次函数策略下耗能最低,其次分别是开口向下Sin函数、分段函数和定常函数。NACA0012翼型的平均升阻比为4.34,在各吸气策略下翼型的等效升阻比均显著提高,与开口向下一次函数策略相比,采用开口向下Sin函数策略时由于其在减阻方面效果略好,因此等效升阻比也较高。总的看来,采用开口向下Sin函数策略可将风力机翼型的净获能效率最大化。

图10 不同吸气策略下翼型气动力系数的变化
Fig.10 Variation of aerodynamic coefficients of the airfoil at different strategies
图11 不同吸气策略下速度流线的对比
Fig.11 Comparison of velocity streamline at different strategies
4 结 论
(1) 在相同动量系数下吸气控制对翼型动态失速的控制效果远优于喷气控制。动量系数为0.02时采用吸气控制可完全抑制失速涡的产生,而喷气控制下翼型在下俯运动中仍存在涡的演化。翼型前缘压差的增大是吸气控制和喷气控制可增升减阻的主要因素。
(2) 动量系数为0.002,在定常函数和分段函数下采用吸气控制具有明显优势,其原因在于NA-CA0012翼型失速涡的演化较集中在下俯过程,因此需要更多的能量来抑制该涡。动量系数为0.02时各吸气策略下气动力系数相差不大,流体也能实现完全附着。

图12 不同吸气策略下耗能系数和等效升阻比的变化
(3) 采用开口向下Sin函数可将风力机翼型的净获能效率最大化。
