基于人工鱼群-径向基神经网络的NOx预测模型

2021-07-17金秀章

动力工程学报 2021年7期

金秀章，于静，刘岳

(华北电力大学控制与计算机工程学院，河北保定 071003)

随着电力需求的不断增长，火电厂所需总煤量增多，生成的氮氧化物增加。为了减少NOx的排放量，避免尿素溶液流量过大导致空气预热器堵塞，或尿素溶液流量过小造成氮氧化物排放超标，必须实时监测氮氧化物的排放质量浓度[1-2]，并对脱硝系统进行优化控制，因此需要建立精度高的预测模型以满足实时监测氮氧化物排放浓度的要求[3]。

已有很多学者对预测模型的建立进行了研究。如高常乐等[4]采用长短期记忆(LSTM)模型对氮氧化物质量浓度进行预测，但LSTM只能处理少量量级，计算费时；秦天牧等[5]采用误差反向传播(BP)神经网络模型和支持向量机(SVM)模型，BP神经网络难以实现全局收敛，SVM模型因其选择参数的复杂性降低了预测效率；方贤等[6-7]采用粒子群算法寻找最优参数组合，其存在容易局部收敛和收敛精度较低的问题；廖永进等[8]采用径向基神经网络(RBFNN)模型，其泛化能力强，可避免局部收敛，并且控制效果也得到了改善；董泽等[9]采用互信息的方法对变量进行筛选，相对于不进行延迟时间筛选的变量提高了预测模型的精度。

因此，笔者采用K-近邻互信息算法对变量的延迟时间进行预估，根据确定的输入变量和输出变量建立RBFNN模型，采用人工鱼群算法(AFSA)优化RBFNN的参数。与粒子群算法相比，AFSA能够克服局部最优解的问题，还能加快运行速度；而RBFNN具有泛化能力强、克服规律不明的输入和全局收敛的特点。结合AFSA和RBFNN算法建立预测模型，不但提高了预测精度，而且减少了运行时间。

1 RBFNN模型

1.1 RBFNN结构

RBFNN具有收敛速度快、克服局部收敛等特点[10]。处理后数据的维数决定网络输入层数；输入变量借助激活函数(径向基函数)从低维度线性不可分映射到高维度线性可分，从而确定网络隐含层；将隐含层输出通过权值向量与输出层输出形成关系。图1是RBFNN结构图。

RBFNN隐含层的激活函数φi(x)采用：

(1)

图1 RBFNN结构图

式中：Xi为输入样本；ci为隐含层第i个神经元的中心向量；di为隐含层第i个神经元的方差。

输出y′为：

(2)

式中：wi为隐含层第i个神经元与输出层的权值向量；h为隐含层节点个数。

1.2 RBFNN训练

RBFNN训练可通过搜寻最优参数来提高预测模型精度。针对基函数的中心向量、隐含层神经元的宽度向量以及连接隐含层与输出层的权值向量[10]3个参数进行如下界定。

(1) 基函数中心向量表达式为：

(3)

式中：Ni为第i组样本总量；M为第i组元素总量；Xij为第i组第j个样本。

(2) 隐含层神经元的宽度di为：

(4)

式中：cmax为最大中心向量。

(3) 连接隐含层与输出层的权值向量wi：

(5)

(4) 将初始的3个参数代入模型，若实际值与预测值的误差未达到最低误差，则需要将这3个参数进行更新：

(8)

式中：cji(t)为第t次迭代第j个隐含层神经元对第i个输入神经元的中心向量；dji(t)为中心向量cjt(t)的宽度；wkj(t)为第t次迭代连接第j个隐含层神经元与第k个输出神经元的权值向量;E为目标函数;η和α为学习因子。

(5) 评价函数为：

(9)

(10)

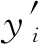
具体的神经网络训练步骤[11]如下：

(1) 归一化训练样本，将上述参数初始化并设置η和α值。

(2) 计算神经网络的输出。

(3) 根据式(9)判断误差是否小于设定值，若小于设定值则终止运行，否则按式(6)～式(8)重新更新参数值。

(4) 返回步骤(2)循环。

2 AFSA-RBFNN模型原理

2.1 AFSA基本原理

AFSA是通过模仿鱼群的觅食行为、聚群行为、追尾行为和随机行为实现全局寻优[12]。假设在一个n维空间，存在N条人工鱼，人工鱼个体状态为Q=(q1,q2,…,qn)，在进行寻优行为时需要确定人工鱼的维数、人工鱼的视野V、人工鱼移动的最大步长s、最大尝试次数T和拥挤度因子δ。根据上述参数执行鱼群的寻优行为[13-14]。

(1) 觅食行为是一种人工鱼在其视觉或者嗅觉允许的范围内趋向食物方向移动的行为，即在当前状态下，若存在某一状态Qj的目标函数小于当前状态Qi：

Qj=Qi+V×rand()

(11)

则按照设定步长向这一状态移动：

(12)

否则保持原状态不变，在设定的视野范围内搜索状态Qj，反复尝试设定最大次数，若仍未前进则执行随机行为。

(2) 聚群行为是一种在不拥挤情况下向邻近人工鱼移动的集体觅食行为，即在视野范围内搜寻邻近人工鱼的数量nf并计算中心位置Qc,若在不拥挤的情况下中心位置的目标函数小于原状态的目标函数，则按照设定步长向这一状态移动：

(13)

式中：Yc为中心位置的目标函数；Yi为当前位置的目标函数。

否则进行觅食行为。

(3) 追尾行为是一种追随周围邻近人工鱼最优位置的行为，即当邻近人工鱼的目标函数小于当前位置的目标函数时，则向邻近人工鱼移动：

(14)

式中：Yj为邻近人工鱼的目标函数。

否则进行觅食行为。

(4) 随机行为如下：

Qi(t+1)=Qi(t)+V×rand()

(15)

2.2 AFSA-RBFNN预测模型

隐含层神经元的宽度、中心向量以及连接隐含层与输出层的权值向量决定了RBFNN模型的精度。利用AFSA对RBFNN的参数进行优化，可以提高模型精度。图2给出了AFSA-RBFNN预测模型流程图。

图2 AFSA-RBFNN预测模型流程图

AFSA-RBFNN预测模型的具体步骤如下：(1)初始化人工鱼群参数，如迭代次数、种群规模等；确定网络结构，初始化RBFNN需要优化的参数；(2)利用初始人工鱼状态调用目标函数计算出最优人工鱼状态，并将最优目标函数值赋予公告牌；(3)通过上述4种行为更新各自人工鱼状态，生成新的人工鱼群；(4)更新所有人工鱼个体，如果某人工鱼个体的目标函数值优于公告牌，则将该个体的目标函数值作为新的公告牌；(5)直到满足终止条件，即满足评价模型精度[15-16]的条件，输出最优人工鱼群状态由测试程序调用，否则返回步骤(3)。

3 AFSA-RBFNN预测模型

3.1 输入变量的选择

选择性催化还原(SCR)脱硝系统的氮氧化物浓度测点分为A、B两侧，由于其两侧变化趋势类似，选取A侧的运行数据进行研究，测得尿素溶液阀门开度、给煤量和送风量等13个影响入口NOx质量浓度的因素。模型输入变量需要与输出变量的相关性进行筛选，若选择多个输入变量会由于信息冗余导致模型精度下降，若输入变量不足则不能完全反映对象特性，因此通过互信息[17-18]筛选出相关系数较大的5个因素：总风量、总煤量、尿素溶液开度、SCR入口烟气含氧量以及SCR入口烟气温度。由于系统本身存在滞后，且影响SCR入口NOx质量浓度的因素较多，从而导致迟延，因此利用K-近邻互信息算法[19]对系统迟延时间进行分析，对训练样本时间进行重构。各输入变量与SCR入口NOx质量浓度的相关系数如表1所示。输入变量迟延时间如表2所示。

3.2 预测模型结构

依据上述新的训练样本相空间，采用隐含层为3层的RBFNN进行辨识，以总风量、总煤量、尿素溶液开度、SCR入口烟气含氧量和SCR入口烟气温度作为输入变量，SCR入口NOx质量浓度作为模型输出变量，然后利用AFSA对RBF神经网络的参数进行优化。预测模型具体结构[20]见图3。

其中，X1(t)、X2(t)、X3(t)、X4(t)、X5(t)分别代表总风量、总煤量、尿素溶液开度、SCR入口烟气含氧量和SCR入口烟气温度，Z-d为时间迟延，d1、d2、d3、d4、d5分别代表5个因素的迟延时间，d1=70 s，d2=62 s，d3=40 s，d4=0 s，d5=0.8 s，y(t)为此时SCR入口NOx质量浓度。

表1 各输入变量与SCR入口NOx质量浓度的相关系数

表2 输入变量迟延时间

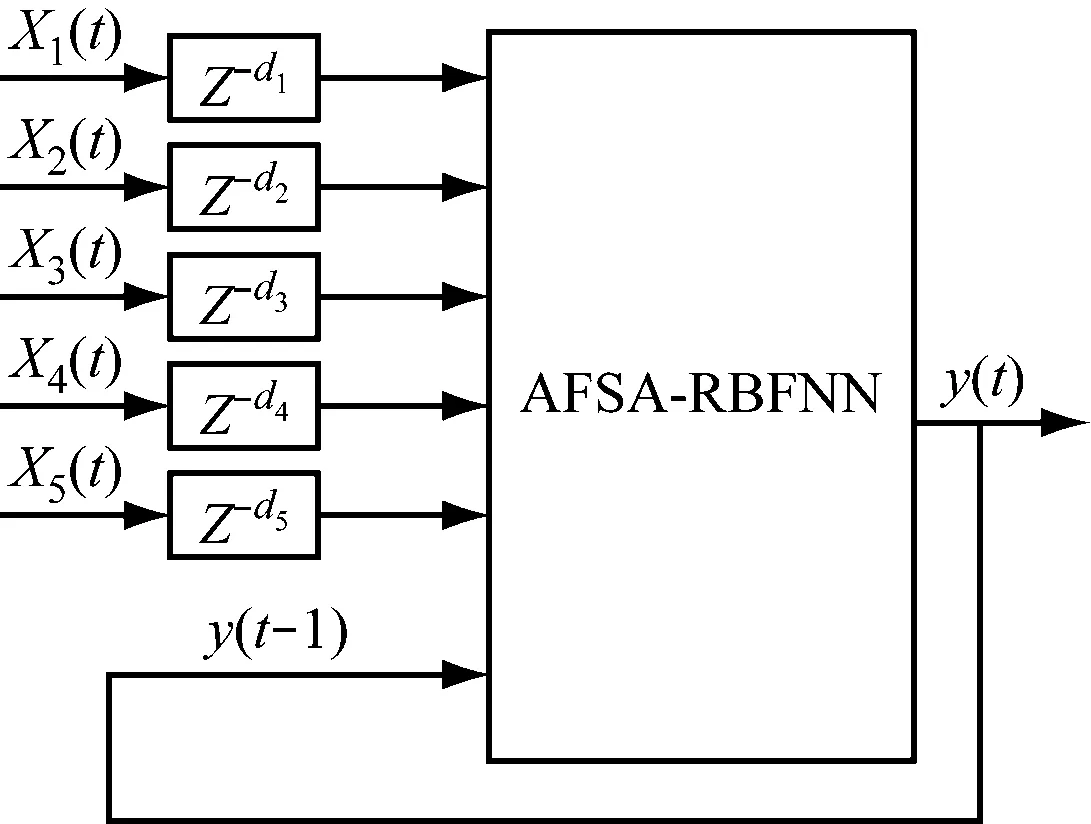
图3 AFSA-RBFNN模型结构图

4 结果与分析

选取某电厂SCR脱硝系统的相关运行数据，截取稳态部分建立AFSA-RBFNN预测模型，总共7 500组数据，前4 000组数据作为训练集，后3 500组数据作为测试集，采样周期Ts=5 s，总选取时间为10.4 h。AFSA的视野V=6,最大步长s=1.5,种群规模N=30，维度dim=21,迭代最大尝试次数T=3,拥挤度因子δ=2。图4给出了训练集和测试集SCR入口NOx质量浓度的预测值和实际值曲线。由图4可知，训练集中，AFSA-RBFNN预测值基本与实际值重合，仅仅在样本序列3 400～3 500存在较小偏差；测试集中，AFSA-RBFFNN预测值在800～900存在略微波动，其他序列的预测值与实际值曲线基本一致，即训练集拟合和测试集预测的精度较高，表明此模型具备强学习和泛化能力。

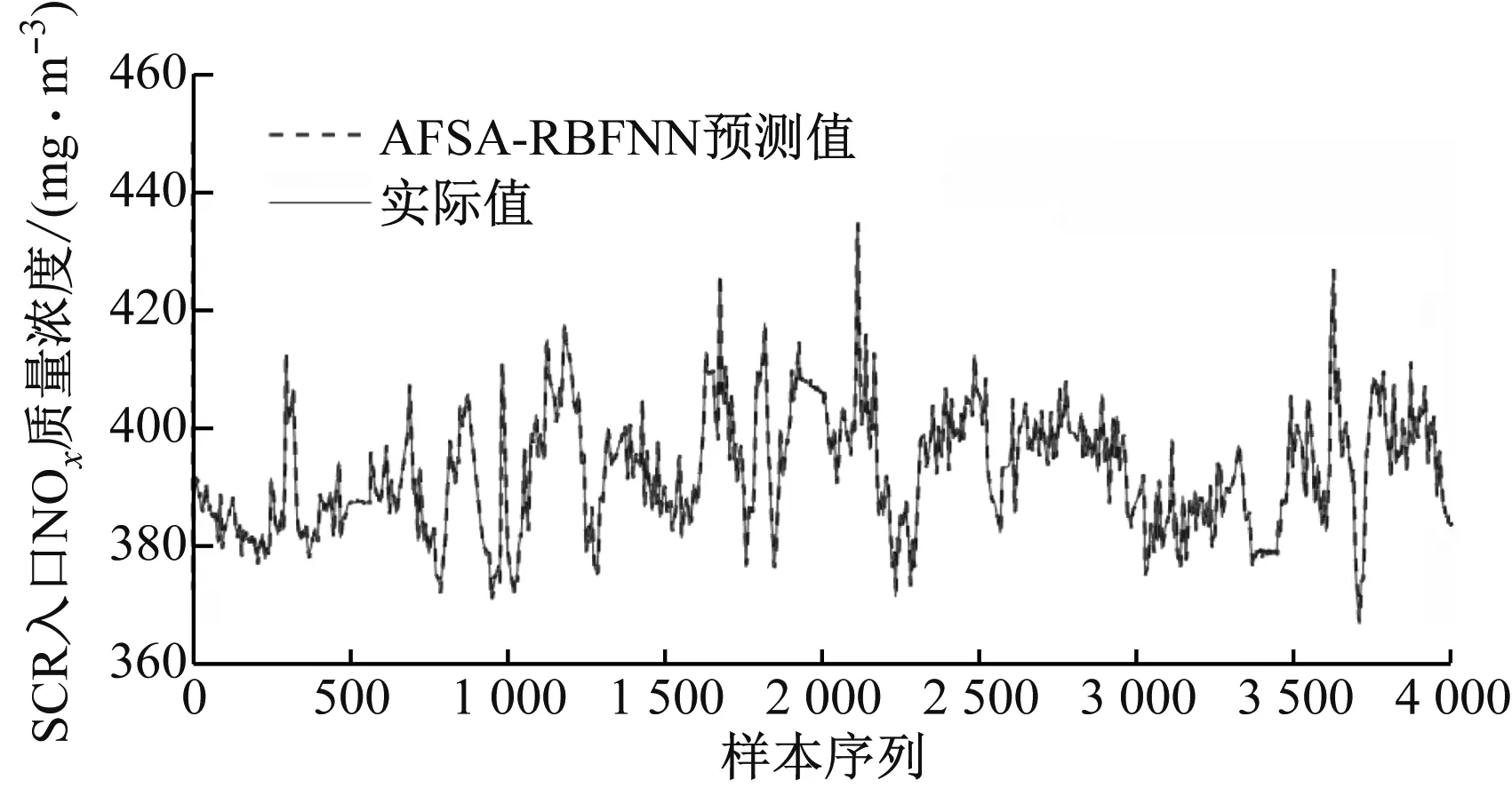
(a) 训练集

(b) 测试集

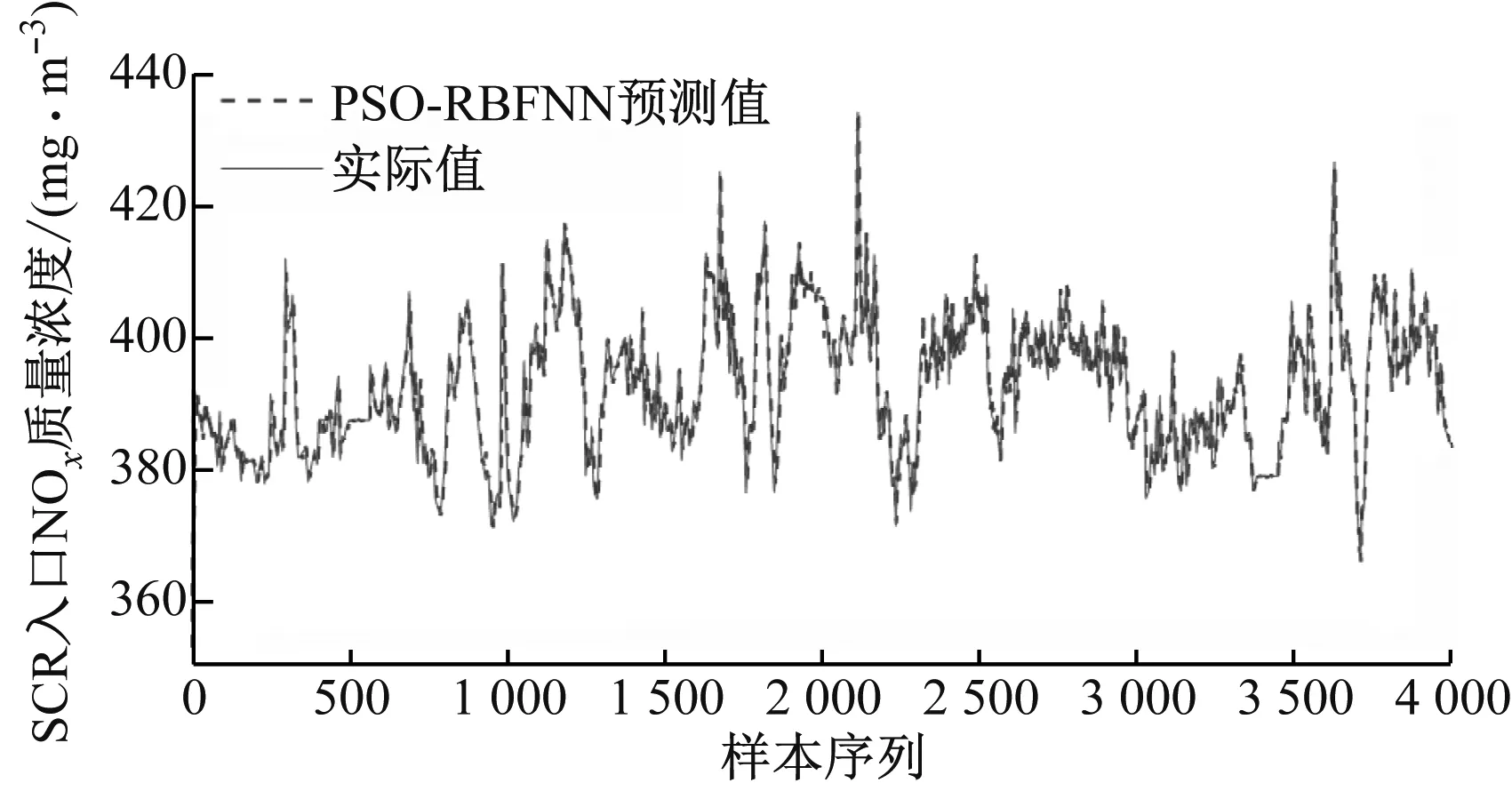
采用上述相同的数据集，分别建立RBFNN、PSO-RBFNN预测模型。各模型训练集和测试集的预测值和实际值曲线如图5和图6所示。

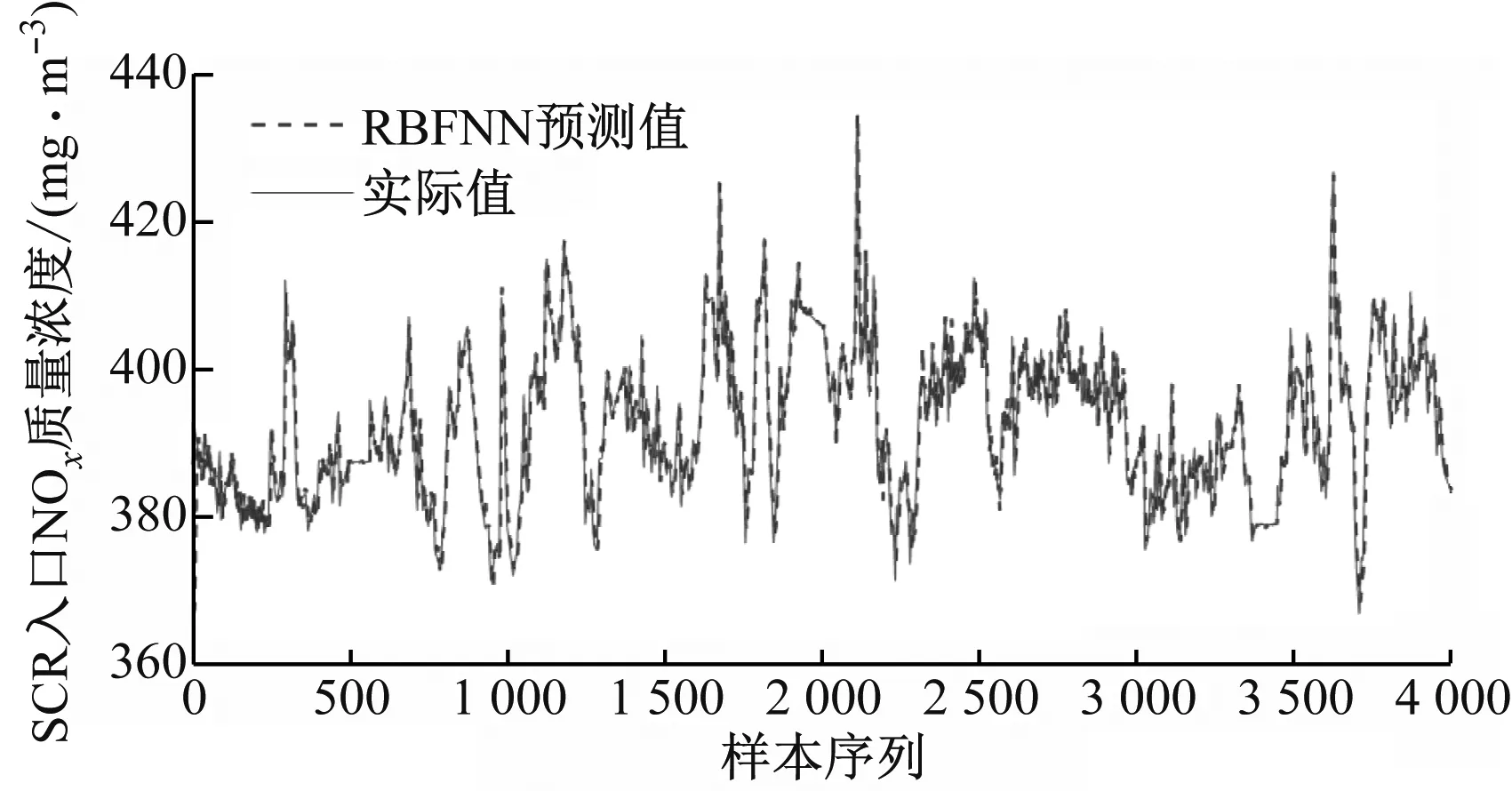
(a) 训练集

(b) 测试集

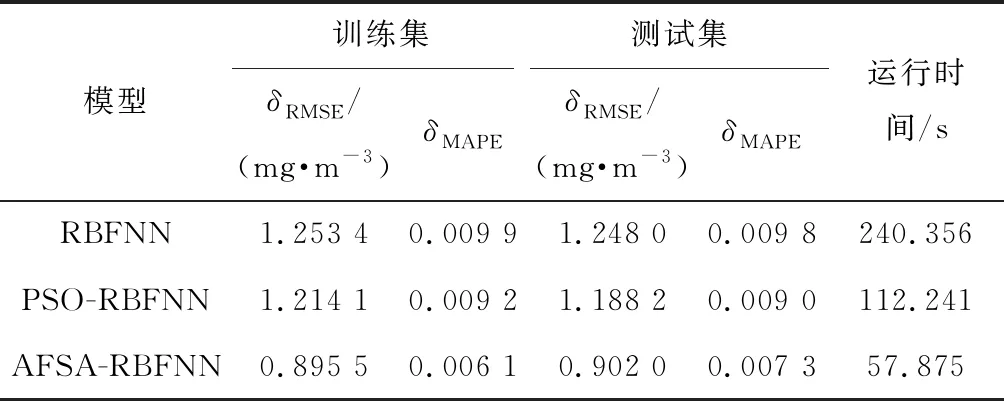
利用均方根误差δRMSE和平均绝对百分比误差δMAPE描述预测模型的精度，各模型精度比较如表3所示。

(a) 训练集

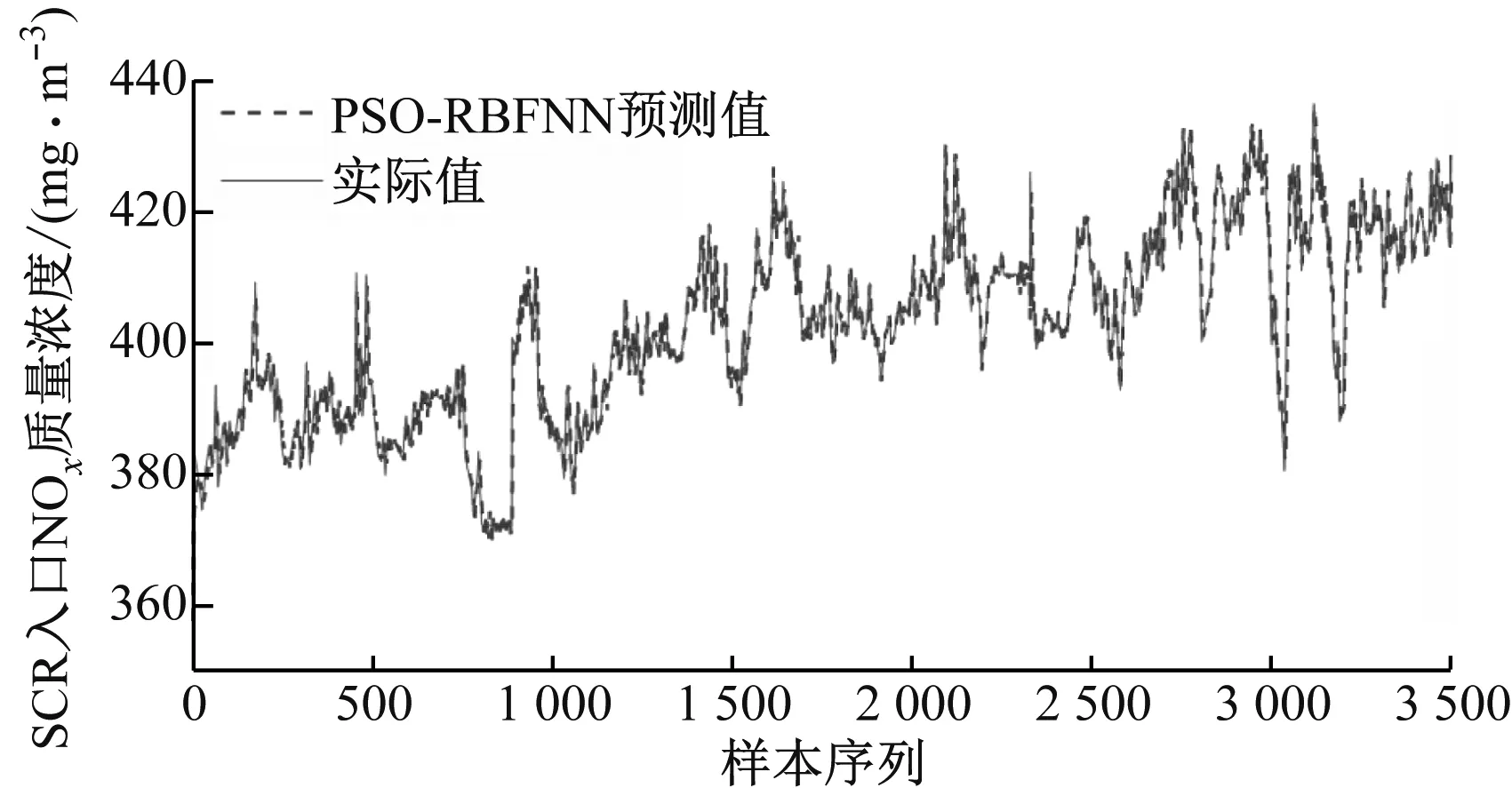
(b) 测试集

模型训练集测试集δRMSE/(mg·m-3) δMAPEδRMSE/(mg·m-3)δMAPE运行时间/sRBFNN1.253 40.009 91.248 00.009 8240.356PSO-RBFNN1.214 10.009 21.188 20.009 0112.241AFSA-RBFNN0.895 50.006 10.902 00.007 357.875

对比图4(a)、图5(a)和图6(a)可以看出，由于数据集达到几万，单独利用RBFNN模型对数据集进行学习造成学习能力下降，图5(a)中实际值与预测值曲线在序列2 300～2 800有明显的波动；而采用人工鱼群算法和粒子群算法优化网络参数后，极大提高了其学习能力，图4(a)和图6(a)中实际值与预测值曲线基本无波动且基本吻合。

从图4(b)、图5(b)和图6(b)可以看出，由于粒子群算法优化了RBFNN参数，减弱了参数随机性造成的模型精度的降低，PSO-RBFNN预测模型的稳定程度明显优于RBFNN预测模型,并且RBFNN在500～600、2 200～2 300以及2 500～2 700范围内的预测精度相对较差，而AFSA-RBFNN预测模型的精度最高，其预测值与实际值之间基本无波动。

从表3可以看出，RBFNN预测模型的均方根误差和平均绝对百分比误差最大，由于需要利用循环程序寻找工具箱的最优隐含层数，RBFNN预测模型的运行时间最长，达到4 min；与RBFNN模型相比，PSO-RBFNN预测模型的训练集和测试集的均方根误差分别减小0.039 3 mg/m3和0.059 8 mg/m3,平均绝对百分比误差分别减小0.000 7和0.000 8，测试时间减少128.115 s。PSO-RBFNN预测模型精度比RBFNN预测模型高；而AFSA-RBFNN预测模型训练集和测试集的均方根误差和平均绝对百分比误差最小,运行时间最短，其训练集的均方根误差为0.895 5 mg/m3，测试集的均方根误差为0.902 0 mg/m3,平均绝对百分比误差分别为0.006 1和0.007 3，运行时间达到57.875 s。

综上所述，AFSA-RBFNN预测模型的学习能力和泛化能力明显优于RBFNN预测模型和PSO-RBFNN预测模型。