低维空间上分片线性函数的逼近因子与剖分数

陶玉杰，由巧俐，李晓萍

(1.通化师范学院数学学院，吉林 通化 134002； 2.辽东学院师范学院数学系，辽宁 丹东 118003；3.天津师范大学管理学院，天津 300387)

2000年，文献[1]通过剖分输入空间首次提出分片线性函数的概念，并以此为工具讨论T-S模糊系统对一类可积函数的逼近性，继而又探究了Mamdani模糊系统对p-可积函数的逼近性能[2-4].但遗憾的是这些结果只是把分片线性函数作为一个桥梁来完成理论证明，并没有给出如何获取这个分片线性函数的方法，这必然限制了分片线性函数的更广泛应用.2014年，文献[5]通过引入诱导算子及其算术运算给出了K-积分模概念，并研究了广义Mamdani模糊系统的泛逼近性.文献[6]在文献[1，5]的基础上进一步给出n元分片线性函数的构造方法及其解析式，并通过矩阵行列式给出了对应方程系数的求解公式.2015年，文献[7]通过引入K-拟减运算建立了Kp-积分模，并由此讨论了分片线性函数逼近一类可积函数问题，继而又以分片线性函数为桥梁研究了广义Mamdani模糊系统对一类Kp-可积函数的逼近性能[8].这些结果对进一步拓宽研究模糊系统的逼近性能具有重要的理论意义.

2017年，文献[9]利用对广义正方体的网格剖分构造了具体的分片线性函数，并证明该分片线性函数在最大范数和矩阵模意义下可以任意精度逼近连续函数.然而，文献[9]对其中逼近因子并没有给出详细说明，只是粗略地把它作为一个常数来处理，这不得不说是一个憾事.本文将针对这个缺陷首先在低维欧氏空间中证明逼近因子与剖分数无关.

1 预备知识

分片线性函数在研究模糊系统逼近性中起着举足轻重的作用，它不仅是1元分段线性函数在多元情况下的推广，而且也是沟通模糊系统和被逼近函数的一个重要桥梁.本文用Rn表示n维欧式空间，N表示自然数集.对给定实数a>0，令

Δ(a)={(x1，x2，…，xn)∈Rn|0≤xi≤a，i=1，2，…，n}，

并称Δ(a)为Rn中边长为a的广义正方体，实际上Δ(a)=[0，a]×[0，a]×…×[0，a]=[0，a]n.

定义1.1[1]设n元连续函数S：Rn→R满足如下条件：

(1) 存在a>0，使S在广义正方体Δ(a)之外恒为零；

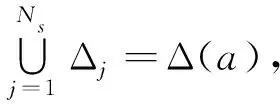
则称S为Rn上一个分片线性函数，其中βij和λj均为常数，i=1，2，…，n.

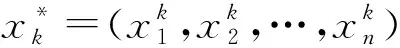
此时，∀x=(x1，x2，…，xn)∈Δi1i2…in，ij=1，2，…，m，j=1，2，…，n，不妨设剖分后每个小多面体Δi1i2…in的n+1个顶点在Rn+1空间上所确定的超平面方程为

(1)

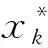
再将Δi1i2…in的n+1个顶点坐标依次代入(1)式，可在Rn+1上获得1组抽象超平面线性方程为

(2)

(3)

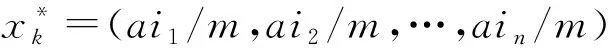
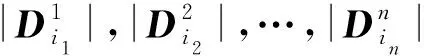
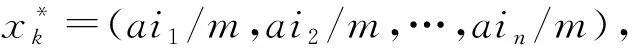
定义1.2 设矩阵A为n阶方阵，令‖A‖=|(|A|)|，则称‖A‖为A的矩阵模，亦即，矩阵模‖A‖即为A的行列式的绝对值.显然，任何方阵A的矩阵模总满足‖A‖≥0.

引理1[9]设f在紧集Δ(a)⊂Rn上连续，(x；f(x))是给定数据对，但f的解析表达式未知，则∀ε>0，存在剖分数m∈N和形如(3)式的分片线性函数S，使其在无穷范数意义下满足

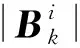
2 主要结果

按照引理1，只有当逼近因子是一个与剖分数m无关的常数，分片线性函数S对所给f才具有逼近性，故这个逼近因子是否与m无关至关重要.然而，文献[9]并没有给出证明，只是粗略地把它视为常数.下面，将针对低维空间(n≤3)证明这个逼近因子确实与剖分数m无关.

当n=1时，将闭区间[0，a]分成m个小区间，使每个小区间长度为a/m.若∀x∈[0，a]，动点x只能落在其中某个闭区间上，不妨设此闭区间为[x1，x2]=[(i-1)a/m，ia/m]，见图1.

图1 n=1时区间长度为a/m的等距剖分示意图

由系数行列式得矩阵模‖D1‖=a/m.进而获得

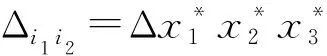
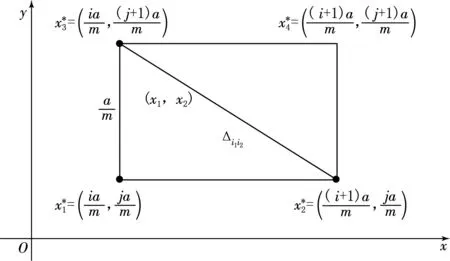
图2 n=2时边长为a/m的小正方形的剖分示意图

按方程组(2)中系数行列式公式得

再由(2)—(3)式计算得：

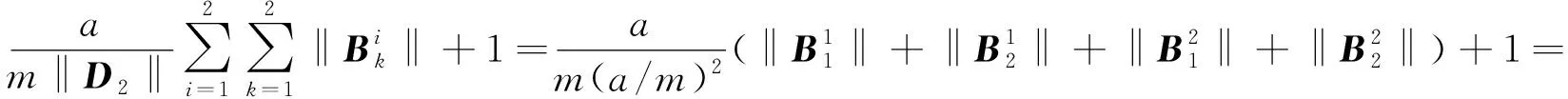
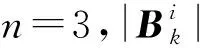
证明当n=3时，将正方体[0，a]×[0，a]×[0，a]等距剖分成边长为a/m的m3个小正方体，再对每个小正方体沿对角面等分成若干小四面体(不计个数)，且直角边长仍为a/m.为简单起见，只在xOy面上给出小正方体Δ(a/m)的等距剖分示意图，参见图3.

图3 n=3时边长为a/m的小正方体Δ(a/m)剖分示意图

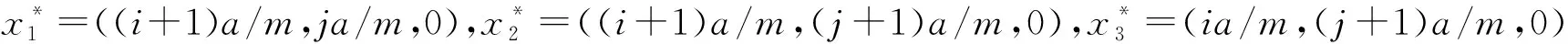
从而矩阵模‖D3‖=(a/m)3.此外，由(2)—(3)式容易获得：

再依据矩阵模定义立刻获得

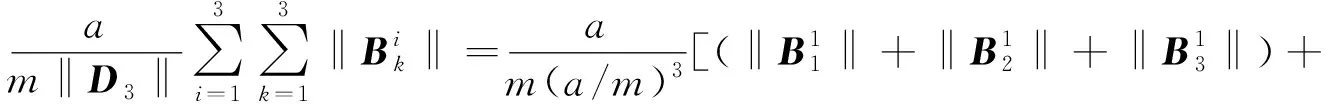
综上所述，对n=1，2，3低维空间来说，逼近因子中所含剖分数m恰好被抵消掉，亦即，逼近因子与剖分数m无关.然而，这到底是偶然还是必然仅凭目前情况尚不能确定.为此，它促使人们猜想在一般情况下逼近因子与剖分数m的取值是否也无关? 对此问题本文暂不予讨论.