基于压扭联轴器的二维缓冲阀的仿真特性研究
2021-07-16度红望张啟晖
刘 神,度红望,熊 伟,张啟晖
(1.大连海事大学船舶机电设备研究所,辽宁大连 116026; 2.江西理工大学机电工程学院,江西赣州 341000)
引言
车辆换挡用缓冲阀作为车辆传动系统的重要组成部分,其作用是保证离合器油腔内油压在换挡过程中有合理的油压特性,从而减小换挡冲击,使驾驶员、乘员有较好的驾驶和乘坐感受。缓冲阀的缓冲效果直接影响整个换挡过程的平稳性,许多学者对不同类型的缓冲阀进行了大量研究。马彪等[1]选取不同结构参数的机械式缓冲阀进行模拟实验,从实验结果可以看出,通过调整结构参数可以有效地控制缓冲时间和缓冲压力。模拟实验中方便调节的参数只有节流孔的大小、缓冲弹簧预压缩量、阀芯的位移量,且调节起来极不方便,所以该方法局限性很大。孟祥政等[2]先通过计算得到机械式缓冲阀的主要结构参数,再利用AMESim进行仿真分析,通过仿真结果与设计要求相对比,验证理论设计方法的可行性;施琪等[3]利用AMESim对机械式缓冲阀建立通用仿真模型并进行仿真分析,较为准确的反映出结构参数对系统特性的影响。结构参数的改变无法解决机械式缓冲阀易污染、易失效以及响应慢、适应性差等缺点,随着电磁技术的发展,电液式缓冲阀逐渐受到关注。MORSELLI等[4]利用功率键合图对含有电液式缓冲阀组的整个回路进行仿真,最后通过试验验证其模型准确性;张英锋等[5]利用AMESim对电液式换挡缓冲阀建立了仿真模型,研究了主油压、电磁阀结构、节流孔直径、阀芯质量等因素对离合器油压的影响,仿真结果说明以上因素均对离合器油压有较大影响;巩招兵等[6]建立了缓冲阀动态数学模型,并利用Simulink对其动态特性进行了仿真分析,分析了油液温度、反馈油孔直径和阀芯的搭合量对缓冲阀动态性能的影响。相对机械式缓冲阀而言,电液式缓冲阀在性能方面有所提高,但控制精度、超调量大、体积过大的问题仍需解决。随着数字技术的广泛应用,阮健等[7]发明了一种全新的2D数字伺服阀,该阀通过螺旋机构将阀芯的旋转运动转换为轴向运动,实现阀的液压功率放大功能同时具备良好的工作性能;2D数字技术在换向阀、高速开关阀[8]等都有应用,张啟晖等[9-10]根据2D数字原理设计了一款缓冲阀,并利用Simulink和AMESim对所建立数学模型进行联合求解,最后通过试验验证联合仿真模型的正确性。研究结果表明,2D数字缓冲阀的各性能指标均优于传统缓冲阀,但由于其传动机构采用开式齿轮传动,容易造成污染导致系统不稳定,传动精度降低。
针对现有2D缓冲阀易污染、传动精度低的问题,本研究设计了一款基于压扭联轴器的二维缓冲阀,并开展联合仿真以验证阀的缓冲特性。
1 缓冲阀的结构和工作原理
为了保证离合器油腔在换挡过程中有合理的油压特性,并且提高输出压力的控制精度,本研究设计了一款将刚性压扭联轴器与二维阀结合的缓冲阀[11],其结构简图如图1所示。
二维缓冲阀主要由电-机械转换器(比例电磁铁)[12]、传动机构(刚性压扭联轴器)、先导阀和主阀组成。比例电磁铁通过内螺纹安装于缓冲阀上,衔铁接头则与楔形件过盈配合;楔形件通过滚轮和滚轮轴与先导阀芯接触连接,轴用挡圈及孔用挡圈用于限制弹簧座位置,弹簧则用在比例电磁铁失电时辅助先导阀芯回到原位;先导阀芯与先导阀套间隙配合,以便于两者之间的旋转运动和轴向运动,先导阀套和阀体之间则是过渡配合,利用钢球将两者之间的滑动摩擦转换为滚动摩擦,便于安装;先导阀芯左端台肩周向开设有高、低压孔槽,先导阀套内开设有斜槽,其中高压孔槽连接压力源,低压孔槽连接油箱,斜槽则与敏感腔相通;主阀结构原理则与传统滑阀结构相似。
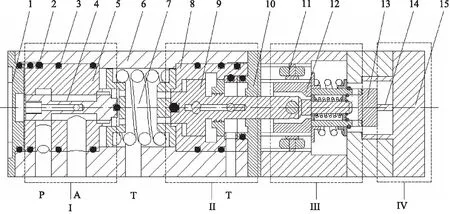
1.端盖 2.钢球 3.O形圈 4.主阀芯 5.主阀套 6.阀体 7.主弹簧 8.先导阀套 9.先导阀 10.端盖2 11.滚轮12.楔形件 13.衔铁接头 14.衔铁 15.电磁铁 Ⅰ.主阀部分 Ⅱ.先导阀部分 Ⅲ.传动机构 Ⅳ.电-机械转换器图1 缓冲阀结构简图
图2为缓冲阀工作原理图。平衡状态时,高压腔截面积为敏感腔截面积的1/2,敏感腔压力由高、低压孔槽与斜槽相交的2个微小菱形面积串联的液压阻力半桥控制。若不考虑摩擦力及阀口液动力的影响,高压孔、低压孔与斜槽相交的面积相等,敏感腔的压力为高压腔压力的1/2,先导阀芯轴向保持静压平衡。当电磁铁通电时,楔形件向左运动,此时由于先导阀芯受液动力影响无法直接被推动,而滚轮的旋转给滚轮轴施加了驱动力偶从而带动先导阀芯逆时针旋转(从右向左看),此时高压孔槽与斜槽相交面积减小,低压孔槽与斜槽相交面积增大,破坏了先导阀芯的轴向静态平衡,导致高压腔的压力高于敏感腔压力,此压力差推动先导阀芯向左运动,主弹簧则将力传递给主阀芯使主阀有一定的开口量,主阀工作原理与减压阀相同,可以根据负载大小调节开口量以保证输出压力稳定,达到缓冲效果;当电磁铁断电时,楔形件右移回原位,此时滚轮轴带动先导阀芯反向转动,敏感腔的压力高于高压腔压力,压力差推动先导阀芯复位,其中复位弹簧起辅助作用。
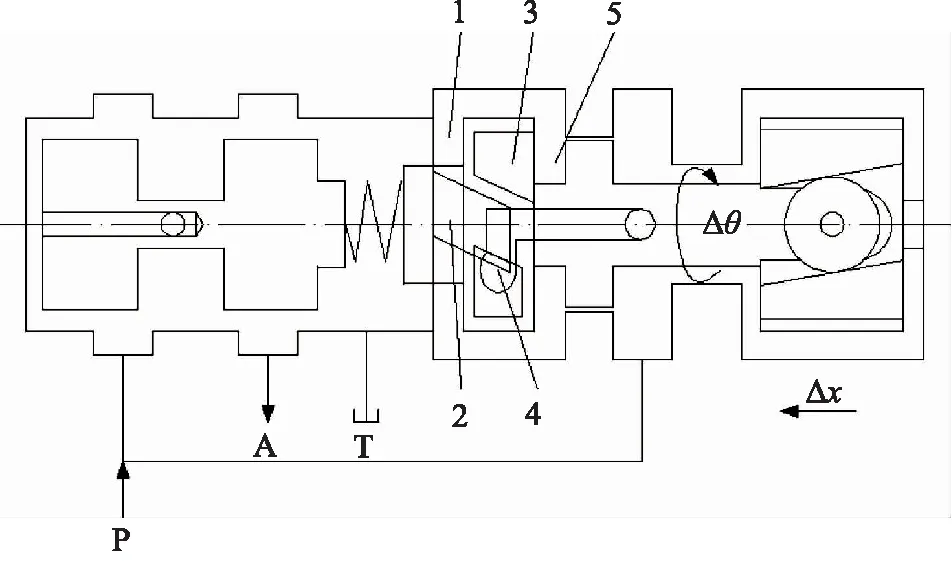
1.敏感腔 2.斜槽 3.低压孔槽 4.高压孔槽 5.高压腔图2 缓冲阀工作原理图
2 缓冲阀的数学模型建立
在建立模型之前,假设:系统工作在稳定状态;流体是理想液体;油源供油压力稳定;忽略泄漏。本研究采用联合仿真,其中压扭联轴器和先导阀部分利用MATLAB/Simulink进行仿真,所以只需建立这两部分的数学模型[13]。
2.1 刚性压扭联轴器数学模型
图3为刚性压扭联轴器受力示意图。刚性压扭联轴器将比例电磁铁的轴向位移转换为先导阀芯的旋转角度,其转换关系为:
(1)
式中,θ—— 先导阀芯旋转角度
xm—— 楔形件的轴向位移
r—— 中心轴传递力的有效半径
α—— 楔形件上斜槽的倾斜角度
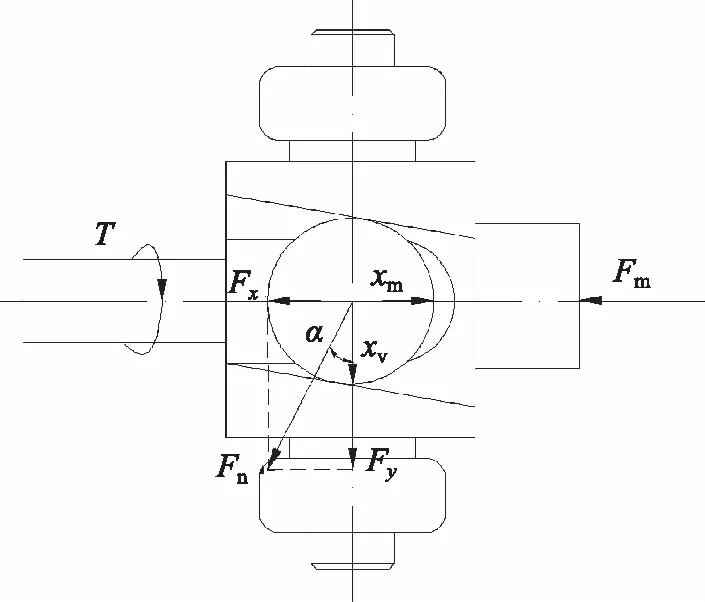
图3 刚性压扭联轴器受力示意图
忽略运动过程中的摩擦力影响,其轴向力-扭矩转换关系为:
T=Fm·r/tanα
(2)
式中,T—— 联轴器输出的扭矩
Fm—— 比例电磁铁对楔形件的作用力
2.2 先导阀数学模型
图4为先导阀工作原理示意图。
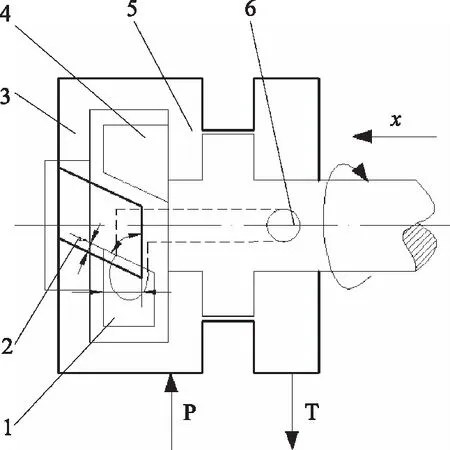
1.高压孔槽 2.斜槽 3.敏感腔 4.低压孔槽5.高压腔 6.回油孔图4 先导阀工作原理示意图
重叠面积:
(3)
式中,h—— 高、低压孔槽与斜槽相交面积的垂直高度
ω—— 高、低压孔槽与斜槽相交面积的轴向宽度
β—— 斜槽倾斜角度
h1=Rθsinβ-h0
(4)
h2=Rθsinβ+h0
(5)
式中,h1—— 低压孔槽与斜槽相交面积的垂直高度
h2—— 高压孔槽与斜槽相交面积的垂直高度
R—— 先导阀芯半径
h0—— 先导阀芯在平衡位置时高、低压孔槽与斜槽的初始垂直高度
将式(3)带入式(4)得变化后高压孔与斜槽相交面积:
A1=Rθω-ωh0/sinβ
(6)
将式(3)带入式(5)得变化后低压孔与斜槽相交面积:
A2=Rθω+ωh0/sinβ
(7)
流进敏感腔的流量q1为:
(8)
流出敏感腔的流量q2为:
(9)
式中,Cd—— 先导阀阀口流量系数
ps—— 进油口压力
pc—— 敏感腔压力
ρ—— 油液密度
假设油液不可压缩,根据流量的连续性原理,先导阀流量方程为:
(10)
式中,AL—— 敏感腔阀芯作用面积
pc—— 敏感腔压力
βe—— 油液体积弹性模量
x—— 先导阀芯位移
Vc—— 敏感腔容积
先导阀芯动力学方程:
(11)
式中,Ar—— 高压腔作用面积
m—— 先导阀芯的总质量
Bp—— 先导阀芯的总黏性系数
Kv—— 负载的弹性刚度
先导阀的旋转与输出位移的关系:
Δh=h-h0=Rθsinβ-xcosβ
(12)
将式(10)、式(11)进行拉氏变换可推导出先导阀传递函数:
(13)
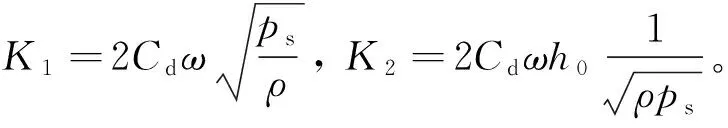
3 联合仿真
AMESim是基于物理模型的仿真软件,其最大优势在于对系统及元件进行物理建模而无需数学模型,可以极大的提高工作效率,但同时AMESim也具有局限性,一些复杂的结构没有相应的模型,比如本研究中的先导阀和传动机构部分,需要手动编辑相应模块,而且控制部分也不好实现,所以采用AMESim与Simulink联合仿真,充分利用两套软件分别在液压系统建模仿真与数据处理能力方面的优势对系统进行仿真分析[14-17]。
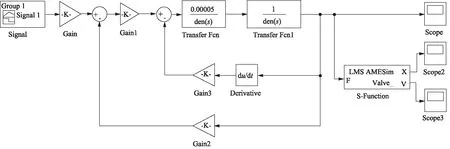
图5 联合仿真Simulink环境下的液压系统模型
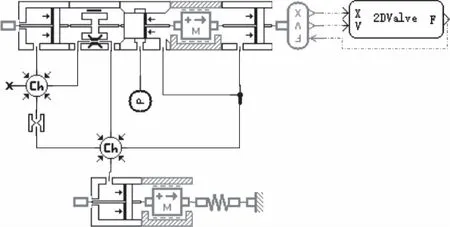
图6 联合仿真AMESim环境下的液压系统模型
3.1 Simulink仿真模型
将数学模型进行线性化处理,然后进行拉氏变换,根据传递函数构建压扭联轴器和先导阀的仿真模型,模型如图5所示,仿真参数设置参照表1。
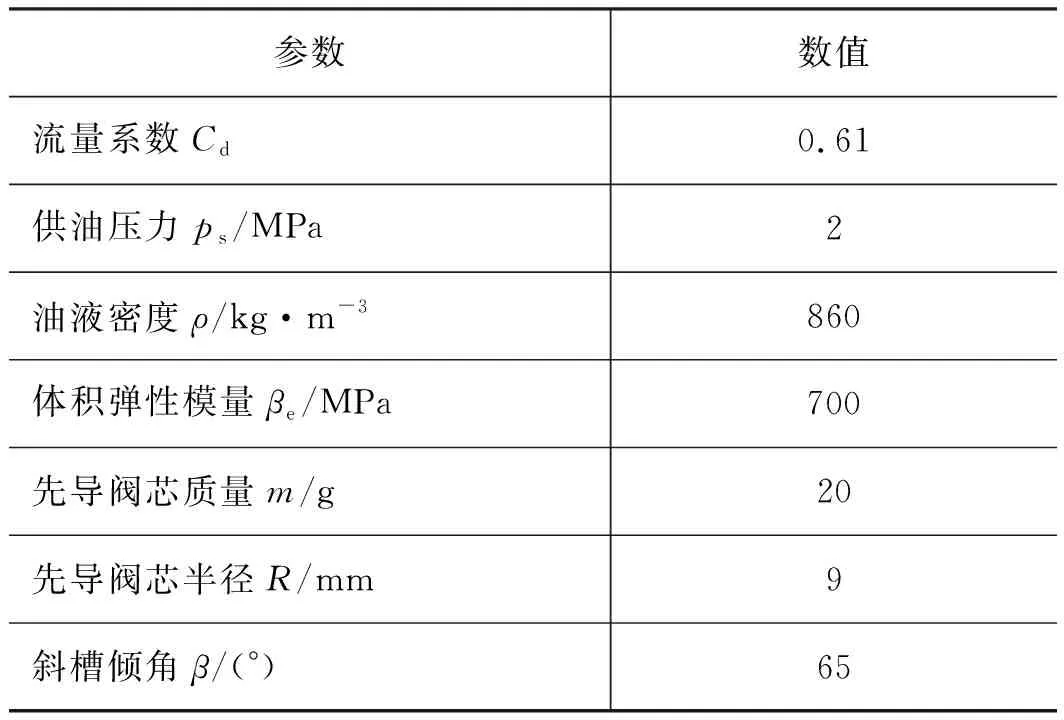
表1 先导阀部分仿真参数取值
3.2 主阀及系统其他元件AMESim模型
液压系统及主阀部分利用AMESim中提供的液压库、液压元件设计库、机械库等建立仿真模型,其中需要特别注意的是Simulink接口模块的设置,整个系统的仿真模型如图6所示。
仿真参数设置参照表2。

表2 主阀部分仿真参数取值
3.3 仿真结果
二维缓冲阀的缓冲特性是本研究仿真的重点,根据湿式离合器的工作原理,可以将离合器油缸的油压变化分为3个阶段:快速充油阶段、缓冲升压阶段和阶跃升压阶段。仿真输入输出曲线对比如图7所示,图中横轴代表时间,纵轴代表缓冲阀输出压力,先导阀芯在比例电磁铁的驱动下旋转角度变化如图8所示,敏感腔压力在工作过程中的变化如图9所示。
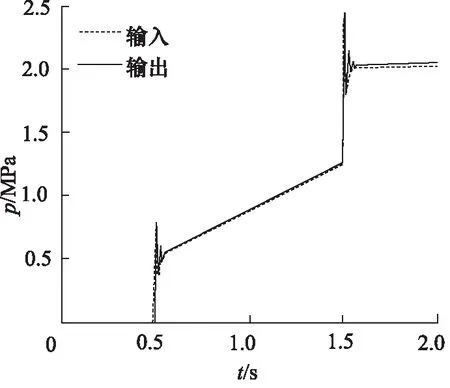
图7 缓冲特性仿真曲线
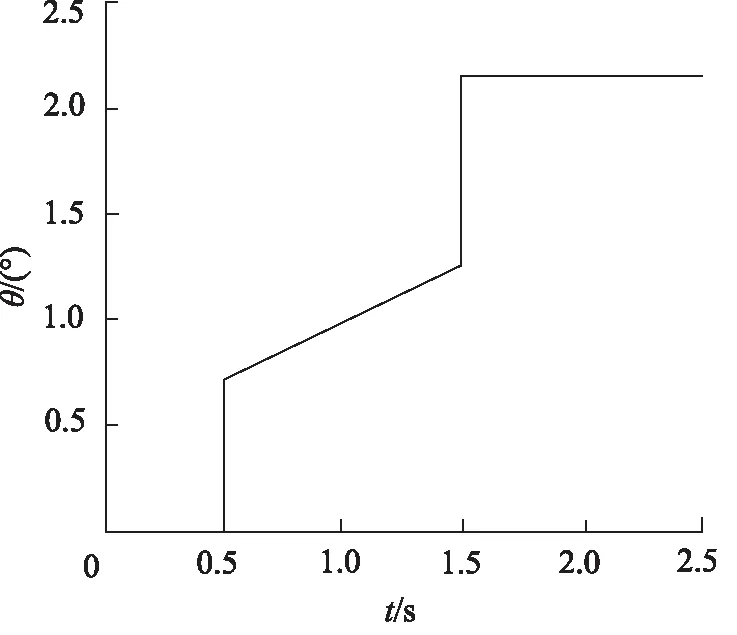
图8 先导阀旋转角度变化曲线
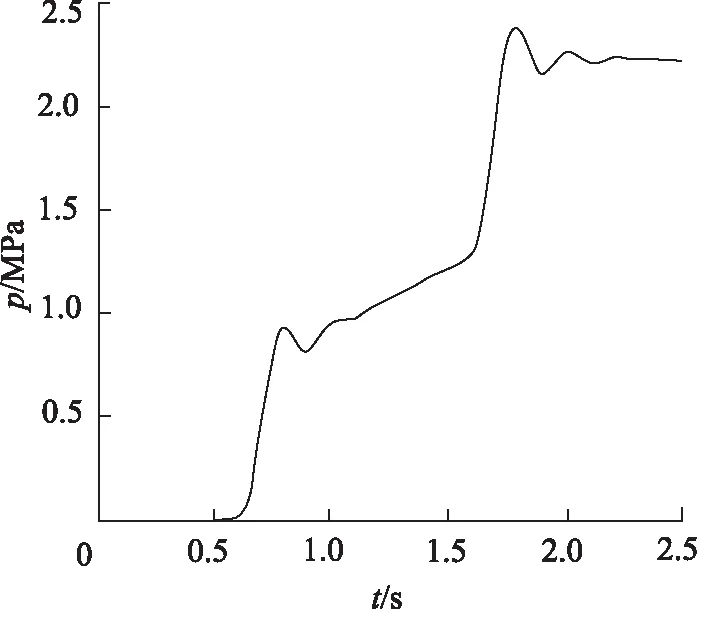
图9 敏感腔压力变化曲线
根据图7~图9可知,缓冲阀在0.5 s时开启,整个缓冲过程在1.6 s内完成,在压力突变的拐点有明显的压力波动,但都能在短时间内趋于稳定。稳定跟随精度η为压力稳定输出时输入信号与输出压力的最大误差率:
(14)
式中,p0—— 缓冲阀稳定输出压力
Ui—— 缓冲阀输出压力稳定时的输入信号
与现有2D缓冲阀的跟随精度4.71%相比有明显提升[10]。仿真曲线证明缓冲阀确实能够使输出的油液压力缓慢上升,并使得进入离合器内的油压与理想曲线一致。
进一步分析其超调量,即最大偏差δ:
(15)
式中,p0—— 输出压力的峰值
Ui—— 峰值所对应的给定值
该二维缓冲阀的超调量22.1%远远小于电液式缓冲阀的超调量105%,并且也优于现有2D缓冲阀的超调量31.2%。
4 结论
本研究对二维缓冲阀整体建立了数学模型,推导出先导阀传递函数,利用MATLAB/Simulink与AMESim联合仿真对该阀的动态特性进行了仿真分析。研究结果表明:
(1) 设计的缓冲阀缓冲过程中的跟随精度为2.13%,与现有2D缓冲阀的跟随精度4.17%相比,有明显提高;该阀的超调量为22.1%,远远小于电液式缓冲阀组的超调量104%,也优于现有2D缓冲阀的31.2%;
(2) 设计的二维缓冲阀具有较短的缓冲时间和稳定的输出压力,有效补偿了换挡冲击,使驾驶员和乘员有更好的驾驶、乘坐体验;同时未来应该向体积更小、反应更迅速、控制更精确的方向发展。
