新型自适应滤波处理方法在动态称重中的应用

沈小倩

(江苏联合职业技术学院 无锡机电分院, 江苏 无锡 214028)

动态称重是指对非静止状态物体的快速测量。动态称重过程中,被测物体称重时间短,受被测物体自身振动、传送带转动、外界随机不确定干扰等作用,真实重量会被淹没在各种干扰载荷中。因此,如何在外界随机不确定干扰作用下准确测量真实重量是动态称重测试系统的核心[1-2]。不同于传统方法,本文采用了时域对消的思路,无须离线设计滤波器[2],创新性地将自适应滤波方法引入到动态称重的低频噪声滤波中,抑制和衰减了噪声干扰,显著提高了信噪比。

自适应噪声抵消技术是基于自适应滤波器的一种应用,能够在外界未知干扰源特征和传递途径不断变化的情况下消减噪声[3]。相互抵消的噪声通常是非线性相关的,这时为了有效去噪就必须采用非线性的自适应滤波[4]。而多层前向BP神经网络能够根据设定精度实现非线性函数逼近,求出滤波系数,构成非线性的自适应滤波器。

在实现方法上,本文将称重信号作为实时通道,无称重时采集的振动和噪声信号作为存储通道,利用自适应滤波器均衡后将两路振动噪声进行抵消,从而提高了信噪比。该方法也为实时抑制信号频段内的噪声干扰提供了一种解决思路。

1 自适应噪声抵消称重系统原理与算法

自适应滤波器是一种能够自动调节本身参数的特殊滤波器,使滤波器输出与理想输出的差异达到最小[5]。

(1)

其中,X(n)=[X(n),X(n-1),…X(n-M+1)]T表示n时刻滤波器的输入信号矢量,H(n)T=[h0(n),h1(n),…hM-1(n)]表示滤波器的权系数,z(n)为滤波器输出,M为滤波器阶数。

1.1 自适应噪声抵消原理[3]

自适应抵消是一种补偿抵消的方法,是基于自适应滤波器原理的一种扩展应用。它以干扰噪声为处理对象,自适应地调整滤波器的传输特性,逐次迭代以获得最优的H(n),其原理如图1。

图1 自适应抵消原理框图Figure 1 Schematic diagram of adaptive cancellation

各变量的时间自变量都以采样序列号n来表示,数字滤波器为参数可调节的滤波器。主通道检测信号y(n)是真实输入信号s(n)叠加了干扰噪声n(n),传感器输出信号为

y(n)=s(n)+n(n)。

(2)

参考通道x(n)经过数字滤波器送到抵消器后得到与称重信号y(n)叠加。滤波器根据自适应算法调整数字滤波器的权系数,补偿噪声源的传输特性差异,均衡两路噪声x(n)与n(n)的不一致,从而使抵消器输出s(n)′尽量逼近要求的信号s(n)。

1.2 新型自适应噪声抵消方法

在动态称重过程中无法得到恒定的噪声源输出,基于这一点,本文设计了新型自适应噪声抵消方法,其实现原理框图如图2。

图2 新型自适应抵消原理图Figure 2 Schematic diagram of new adaptive cancellation

其中,测x(n)的方法是使s(n)=0,即将无称量的空载信号作为噪声源输出,称重信号作为主通道。由于只用一个传感器,x(n)是历史数据,也可以理解为噪声源延时后的输出,经过自适应滤波后送入抵消器,与实时信号抵消。实际应用中,用阈值来判断是否有重物通过,简单易实现。当判断连续L个采样值中不包含重物信号时则更新存储通道,配合主通道进行自适应噪声抵消,同时还能够减小零漂的影响,保持系统长时间运行的补偿效果。L的值可以根据实际运用选取,令L≥M。

在系统中,我们认为s(n)和n(n)不相关,而n(n)和x(n)相关[5]。忽略了两路噪声分量频率不同,认为仅有幅值和相位的差异。

实际输出与理想信号的误差为

e(n)=d(n)-z(n)=d(n)-XT(n)H(n)。

(3)

y(n)为滤波器输出,d(n)为输出期望值。本文采用最小均方误差准则,目标使E{|e(n)|2}最小。而由相似性可证明,必须使E[(n(n)-z(n))2]达到最小,最终转换为对权系数H(n)的调节,求出最佳滤波系数。

1.3 自适应滤波算法

使E[(n(n)-z(n))2]达到最小采用BP神经网络算法,将求最佳滤波器系数问题转化为求解神经网络连接权值的问题,其实现原理如图3[6]。

图3 单输入横向自适应滤波器原理图Figure 3 Schematic diagram of single input transverse adaptive filter

BP神经网络把一组样本的输入、输出问题变为一个非线性优级化问题,在有导师监督下进行学习。期望响应信号d(n)是导师信号,通过误差信号e(n)的反向传播自适应地调节网络结构参数,按梯度下降方向迭代误差,使之达到设定的要求。抵消系统能给出在最小均方意义下对原噪声信号的最佳近似,从而使滤波系统得到高信噪比的输出信号。单隐层的BP前馈网络可以实现任意非线性映射,而增加隐层数会导致运算量增加,所以本文构造三层的BP网络。其中隐含层转移函数为tansig,将神经元的输入范围(-∞,+∞)映射到(-1,+1)。

(4)

输出层选择purelin函数,输出范围转换成(-∞,+∞)。

f(x)=x。

(5)

2 应用实例

2.1 仿真效果

称重模型可等效为一个二阶系统,静态物理建模单位阶跃响应如图4(a)。在理想模型上叠加了均值为0,方差为0.1的高斯白噪声,如图4(b)所示。根据本文提出的基于BP神经网络的非线性自适应抵消滤波算法,以Matlab为平台,有效抑制了噪声干扰,滤波后效果如图4(c)。

图4 滤波在仿真中的效果Figure 4 Effect of filtering in simulation

2.2 在动态称重中的应用

如图5(a)是2个2 kg重物依次经过称重平台[7]时采集的称重信号,称重皮带长1 m,重物称重时间为0.75 s。动态称重信号集中在低频,结合实际应用本系统采样频率取500 Hz。图5(b)为空载情况下采集的噪声信号。图5(c)是经过自适应噪声抵消滤波后输出的信号。

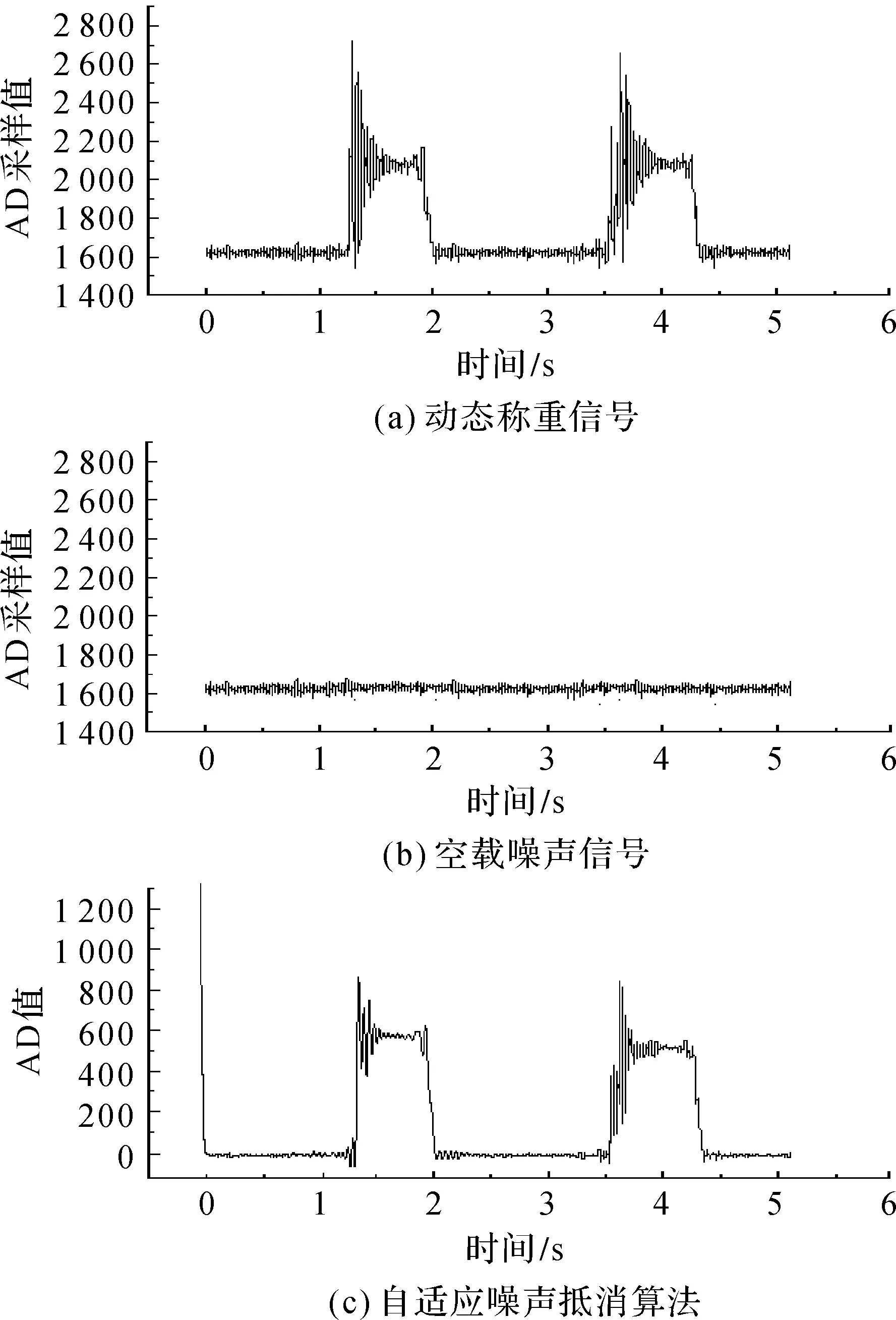
图5 动态称重信号自适应噪声抵消滤波Figure 5 Adaptive noise cancellation algorithm

由图5(c)得:

1) 初始有一个迭代过程并迅速完成收敛;

2) 称台重量在抵消时被消去,所得输出与称重平台重量无关;

3) 噪声干扰得到了有效的抑制,最大限度的复现了原始信号。

迭代过程中有三个参数对训练过程与预测值有影响,分别是训练目标、步长因子和滤波器阶数M。理论上来说,设定的训练目标值越准确则完成训练的网络模型越接近真实,但目标过高则可能导致不能完成训练。权衡训练步数(在10步以内完成训练)目标设定为10-1;学习速率影响着网络的训练速度,经验值取0.01～0.8,不同速率取值训练效果如表1;M表示滤波器的阶数,在自适应噪声抵消中一般取10到50较合适,本实验取24阶。

表1 不同学习速率对应网络训练特性

自适应噪声抵消滤波的目的是降低噪声的影响,当降噪后与理想信号具有同等的光滑性评价和相似性时,降噪性能越好。

为了评价降噪性,本节使用以下三个量化指标。

1) 消噪后降噪信号的能量成分PER,如式(6):

(6)

2) RMS降噪信号与原信号的均方根误差,如式(7):

(7)

REM表示滤波后与理想信号的相似度,其值越小则相似度越高。

3)信噪比SNR。SNR代表了有用信号所占的分量,如式(8)。

(8)

本文与基于海明窗的FIR低通滤波方法作为比较,以物理建模(理想模型)为参照量化分析得到的能量成分、均方根误差和信噪比的值如表2。

表2 不同滤波方法对应性能参数

从表中看出,低通滤波单纯对频谱不加区分地过滤掉,效果不佳。与之相比,自适应噪声抵消无须考虑截止频率的问题,不但降噪后能量比前者高,而且保留了更高的与原信号的相似程度,能够在保留更多细节信号以提高信号能量的前提下,最大限度的反映了理想信号本身的性质,去除噪声与提高信噪比(SNR相比FIR滤波提升20 dB左右),优于传统的滤波方法。而相比较于线性自适应噪声滤波器,基于BP神经网络的非线性的自适应滤波器滤波效果更好,具有较大实用价值。

试验表明,基于BP神经网络的新型自适应滤波方法能够有效抑制动态称重有用信号频带内噪声,同等误差条件下相对提高了可使用的称重速度,同时相对降低了对工装皮带平稳性的要求,尤其在快速称重场合即信噪比较大的场合有较好的滤波效果。

3 结 论

从表2中看出,低通滤波单纯对频谱不加区分地过滤掉,效果不佳。与之相比,自适应噪声抵消无须考虑截止频率的问题,不但降噪后能量比前者高,而且保留了更高的与原信号的相似程度,能够在保留更多细节信号以提高信号能量的前提下,最大限度地反映了理想信号本身的性质,去除噪声与提高信噪比(SNR相比FIR滤波提升20 dB左右),优于传统的滤波方法。而相比较于线性自适应噪声滤波器,基于BP神经网络的非线性的自适应滤波器滤波效果更好,具有较大实用价值。

试验表明,基于BP神经网络的新型自适应滤波方法能够有效抑制动态称重有用信号频带内噪声,同等误差条件下相对提高了可使用的称重速度,同时相对降低了对工装皮带平稳性的要求,尤其在快速称重场合即信噪比较大的场合有较好的滤波效果。