一种基于指令修正的有源电力滤波器控制方法
2021-07-16刘楚晖叶昕炯华新强石祥建
刘楚晖,叶昕炯,华新强,石祥建
(1.南京南瑞继保电气有限公司,南京 211102;2.国网浙江省电力有限公司湖州供电公司,浙江 湖州 313000)
0 引言
随着电力电子技术的进步,基于全控开关器件的有源电力滤波器凭借其响应的快速性、补偿的精确性等诸多优点,成为电力系统谐波抑制领域重要的解决方案之一[1-5]。
基于低压有源电力滤波装置的行业标准JB/T 11067—2011 中明确规定,在负载电流畸变率大于20%的情况下,有源电力滤波器需要对2~25 次谐波进行全补偿,补偿率需要大于85%。因此,有源电力滤波器控制系统的电流环需要具有较高的截止频率,才能对频率远高于50 Hz 的电流指令实现无差跟踪。常用的电流环控制方法包括滞环控制[6-7]、PR(比例谐振)控制[8-9]、重复控制[10-11]、单周控制[12-13]和滑模控制等[14-15]。
以上各种控制方法可以分为线性控制和非线性控制2 种,都是从控制器本身出发进行设计,从而使得控制系统的输出量精确跟踪控制系统的输入量。对于线性控制系统,按照经典控制理论,输出量的频域模型可以表征为输入量的频域模型与控制系统闭环传递函数的乘积。因此,上述各种线性控制方法本质上是让设计好控制器后的整个控制系统的闭环传递函数在各个待补偿谐波频率处幅值近似为1,且相位近似为0°或360°的整数倍。对于有源电力滤波器,控制系统的输入量为负载谐波电流瞬时值的相反数,输出量为自身输出的谐波电流瞬时值。文献中已经提出多种谐波检测提取方法[16-18]。在线性控制系统的框架下,如果不仅检测输入量各次谐波频率处的幅值和相位,而且同时检测输出量各次谐波频率处的谐波幅值和相位,比较两者的幅值和相位差异并修正输入量的幅值和相位,那么根据线性控制系统的性质,最终的输出量理论上也可以精确跟踪原始的输入量,即负载谐波电流的瞬时值。
综上,本文首先建立有源电力滤波器电流环控制系统模型,在采用单50 Hz 比例谐振调节器的线性控制系统框架下,提出一种基于指令修正的有源电力滤波器控制方法,并通过功率实验对稳态谐波补偿精度进行测试,以验证所提方法的有效性。
1 电流环控制系统模型
本文考虑的有源电力滤波器拓扑为常规的二极管钳位式I 型三电平三相四线结构,采用LCL滤波器并网,三相可独立控制。图1 为有源电力滤波器具体拓扑,其中L1为变流器侧滤波器电感,L2为网侧滤波器电感与电网阻抗之和,C 为滤波器电容,Ug为电网电压。

图1 有源电力滤波器拓扑
单相电流环控制系统模型如图2 所示。其中Gi为电流环调节器,Gd为控制系统延时,Uc为滤波电容电压,Iref为电流环目标值,Ig为实际并网电流。

图2 电流环控制框图
化简该控制框图可以得到并网电流关于电流指令和电网电压的传递函数:

式中:T(s)和Zi(s)分别为电流环开环传递函数和单相输入阻抗;s 为拉式算子。
由式(1)可知,为了实现有源电力滤波器对电流指令的无差跟踪,要求电流环开环传递函数在基波和各次谐波频率处增益足够大。简单的方式是在各个特征频率处增加谐振调节器并且增加单一的比例调节器以加快系统的响应速度。
但同时考虑电流环的稳定性,要求电流环在开环截止频率处具有足够的相位裕度。使用多谐振调节器在各特征频率处取得高增益有两方面缺陷:谐振调节器在高于谐振点的频率范围内引入负相移,会导致相位裕度进一步减小;若需补偿的高次谐波频率高于开环截止频率,则电流环不可能保持稳定。
为了实现对高次谐波的精确补偿,通常采用以下3 种方式:
(1)电流滞环控制。这种直接电流控制方法会导致开关频率变化,增加滤波器设计难度,电流波形在开关频率处于低点时出现失真。
(2)比例谐振控制。仍采用这种间接电流控制方法,但提高开关及控制频率。该方法对处理器性能和热设计提出了更高要求。
(3)重复控制方法。这种方法需要精细设计补偿器和内模函数。一方面,为了保证内模的稳定性,一般内模函数模值小于1,这在理论上无法实现无差跟踪。另一方面,补偿器的设计与有源电力滤波器的模型相关,考虑实际成本和体积,LCL 滤波器电感特性无法在额定电流全范围内保持恒定,通常随着电流瞬时值的上升而下降,而电网阻抗也在一定范围区间内变化。以上各种因素都导致建模准确性受限,从而影响谐波补偿效果。
综上,本文提出一种基于指令修正的单比例谐振调节器有源电力滤波器控制方法,对于硬件参数变化具有适应性,并且控制频率和开关频率固定。
2 基于指令修正的控制方法
2.1 基本思路
该控制方法中电流环调节器采用比例调节器与单50 Hz 处的准谐振调节器,调节器具体传递函数为:

式中:kp为比例项增益;kr为谐振项增益;ω1为基波圆频率;ωc为谐振项带宽。
根据式(3),由于基波频率处增加了谐振调节器,使得50 Hz 处的输入阻抗幅值很大,可以忽略50 Hz 电网电压对输出电流50 Hz 分量的影响,所以并网电流近似由电流指令和电流环闭环传递函数决定。以H(s)表征闭环传递函数,实际并网电流表达式如下:
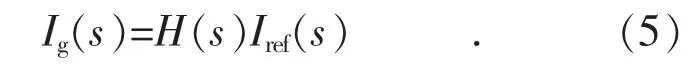
由于电流环在谐波频率处无额外谐振调节器,开环传递函数增益有限,对各次谐波无法进行无差跟踪。对于频率为ωr的谐波,令s=jωr,将式(5)改写成式(6)形式:

式中:Aref和Pref分别为谐波电流指令的幅值和相位;Aerr和Perr分别为实际有源电力滤波器生成的谐波电流相对于指令偏差的幅值和相位。
采用比例谐振调节器进行电流环控制的有源电力滤波器,其本质上是一个线性定常系统。基于此种系统特点,若是同时检测谐波电流指令和实际有源电力滤波器生成的谐波电流两者的幅值偏差和相位偏差,并且使用偏差对谐波电流指令进行修正,则可以直接控制实际电流跟踪电流指令。指令修正方式如下:

式中:Iref_new(ωr)为经过修正后的新指令。
2.2 具体算法
算法流程具体分为3 个部分:第1 部分进行采样数据存储,第2 部分进行谐波指令和实际电流偏差的相位幅值计算,第3 部分进行谐波指令修正。
2.2.1 采样数据存储
不失一般性,假设有源电力滤波器的控制频率、开关频率和采样频率完全一致,即每个PWM(脉宽调制)中断周期采样一次。
设工频周期为控制周期的N 倍,控制周期为Ts,流进有源电力滤波器的某相电流瞬时值为Iapf,有源电力滤波器并网点的其余负载总电流为Iload。
对于Iapf使用2 个长度为N 的数组分别存储实部和虚部,数组名分别为APF_Re 和APF_Im;对于Iload,同样使用2 个长度为N 的数组分别存储实部和虚部,数组名分别为Load_Re 和Load_Im。使 用aAPF_Re_Sum,aAPF_Im_Sum,aLoad_Re_Sum和aLoad_Im_Sum这4个变量分别存储之前4 个数组APF_Re,APF_Im,Load_Re 和Load_Im 的所有元素之和。
以标准傅里叶算法提取第n 次谐波,在t=kTs时刻,设上述4 个数组指针位置均为i,按式(8)和式(9)对4 个数组数据进行更新:
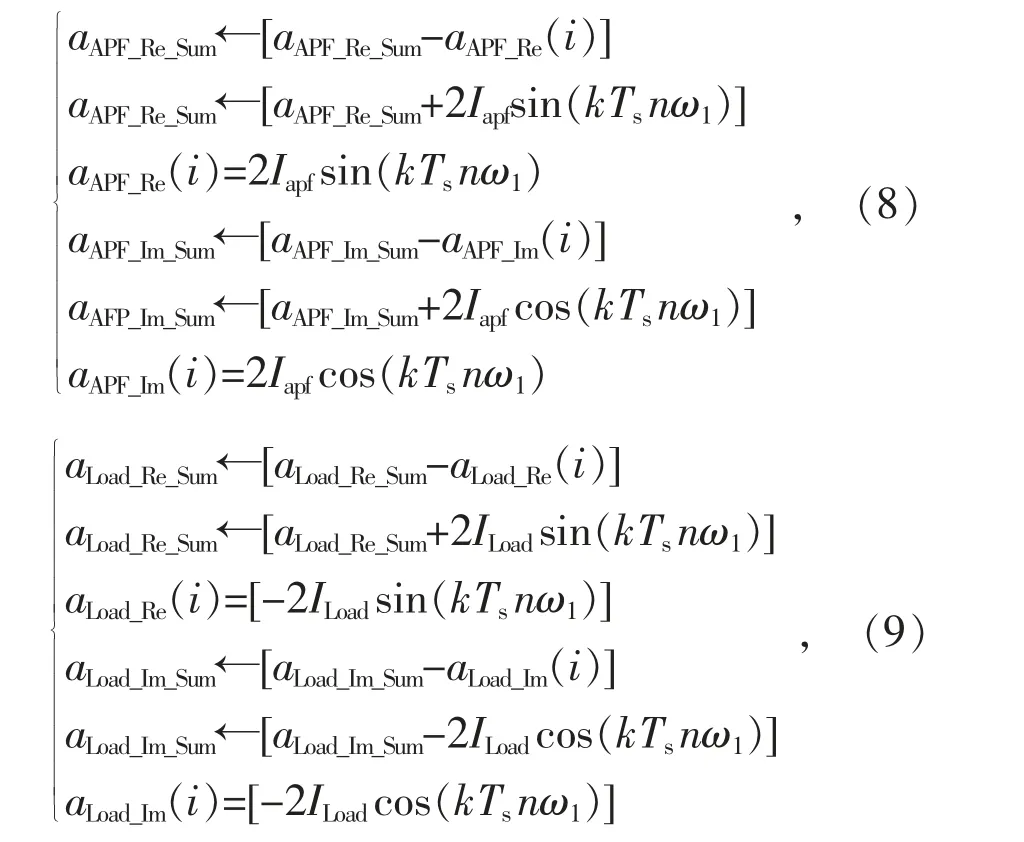
式中:aAPF_Re(i),aAPF_Im(i),aLoad_Re(i),aLoad_Im(i)分别为APF_Re,APF_Im,Load_Re,Load_Im 这4 个数组中的第i 个元素。
在t=(k+1)Ts时刻,数组指针加1,若超过N,则移位到1。
2.2.2 偏差计算
根据傅里叶分解原理,若采样值中含有基波和多种谐波成分,必须连续采样一个基波周期时间才能分别提取出基波和所有谐波成分。所以偏差计算可以每个基波周期进行一次。
幅值偏差按式(10)计算,相位偏差按式(11)计算。

2.2.3 指令修正
根据式(7)并综合式(10)和式(11),可以得到如式(12)所示的修正后指令,该指令每个控制周期计算一次,作为电流环的目标值。
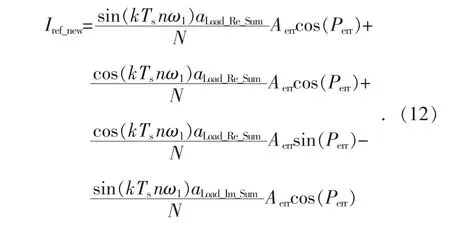
3 实验结果
基于上述理论分析,研制了一台采用图3 所示拓扑的三相四线有源电力滤波器。额定相电流为75 A,额定相电压为220 V,开关频率和控制频率均固定为20 kHz。

图3 样机外观
实验分3 类,第1 类实验研究指令修正算法的有无对于指定次谐波补偿精度的影响,第2 类实验研究指令修正算法对于各高次谐波是否均有提高补偿精度的效果,第3 类实验验证算法对多次谐波复合补偿能力。
3.1 第1 类实验
采用继电保护测试仪给有源电力滤波器提供负载二次电流的采样,二次电流的有效值为1 A,频率为850 Hz,对应17 次谐波,有源电力滤波器负载电流采样TA(电流互感器)变比设置为15,即理想的有源电力滤波器应发出有效值为15 A的17 次谐波电流。
图4 和图5 分别为不采用和采用指令修正算法后对17 次谐波的实际补偿波形。
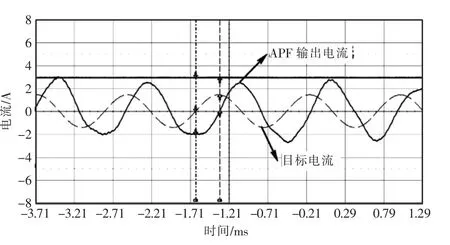
图4 不采用指令修正算法
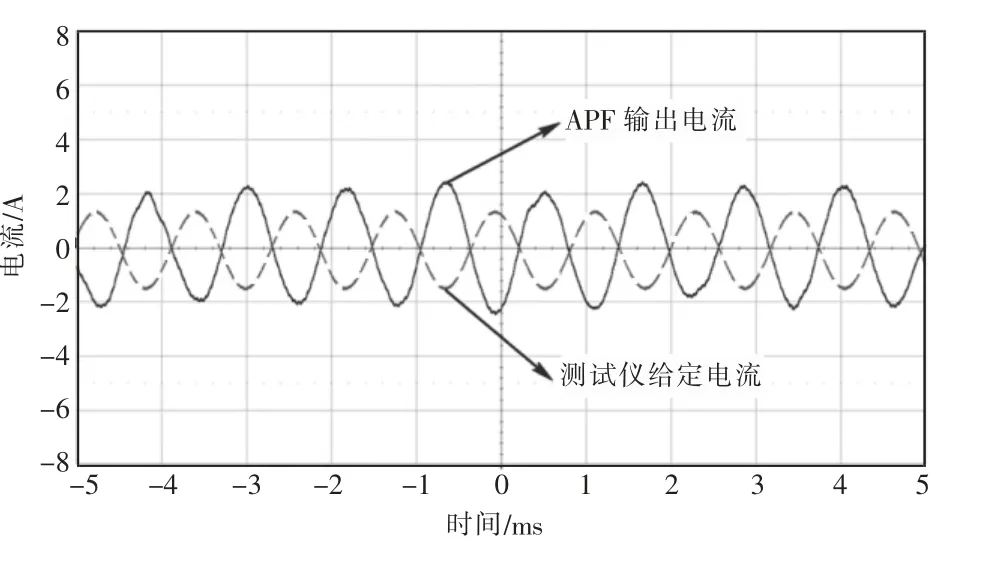
图5 采用指令修正算法
从图4 和图5 可以看出,不采用指令修正算法时,有源电力滤波器产生的电流有效值为17.38 A,电流近似滞后312.6 μs,采用指令修正算法后,有源电力滤波器产生的电流有效值为15.20 A,电流无明显滞后。
3.2 第2 类实验
在采用指令修正算法的前提下,继续对19次、23 次和25 次谐波的单次补偿精度进行实验,结果如图6—8 所示。使用Lecroy 示波器定性观测补偿的相位准确度,使用日置功率分析仪PW6001 定量测量补偿的幅值准确度,TA 变比设置为60,负载二次电流有效值为0.5 A,即理想的有源电力滤波器应发出有效值为30 A 的各次谐波电流。
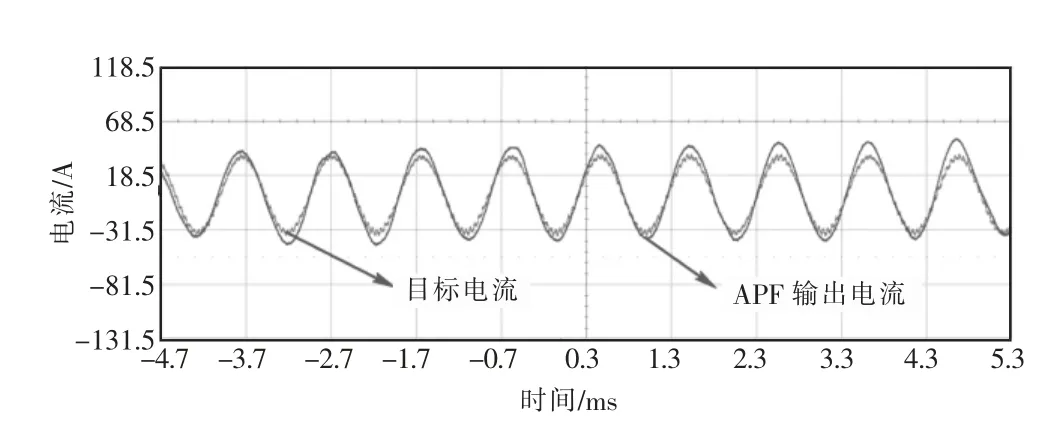
图6 19 次谐波补偿效果
从图6、图7、图8 可以看出,采用指令修正算法后,对于19 次、23 次和25 次谐波,有源电流滤波器输出的对应次谐波有效值分别为29.84 A,29.82 A 和29.73 A,非常接近理想值30 A,同时相位也基本吻合反相后的负载二次电流。
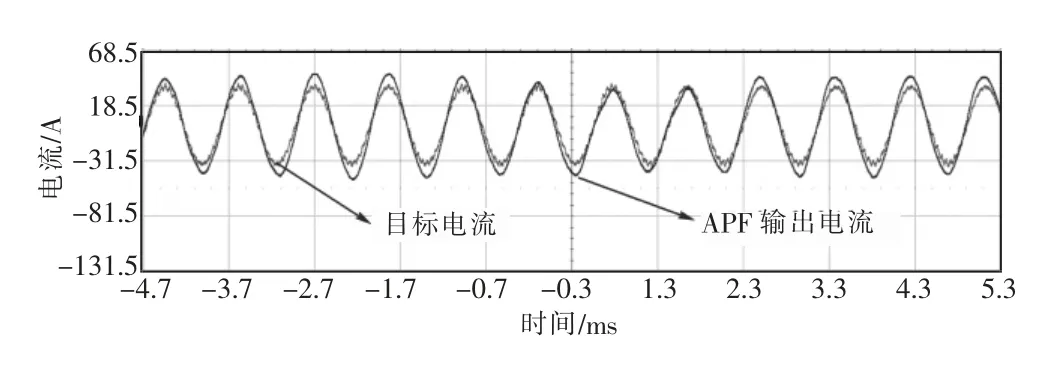
图7 23 次谐波补偿效果

图8 25 次谐波补偿效果
3.3 第3 类实验
为验证指令修正算法对多次谐波复合补偿能力,采用实际的三相整流桥非线性负载进行功率实验,该负载可生成6n±1 次谐波,设定有源电力滤波器的补偿谐波范围为2~25 次,补偿前后网侧电流谐波含量如表1 所示。每相总谐波补偿率均满足JB/T 11067《低压有源电力滤波装置》规定的总谐波补偿率不小于85%的要求。
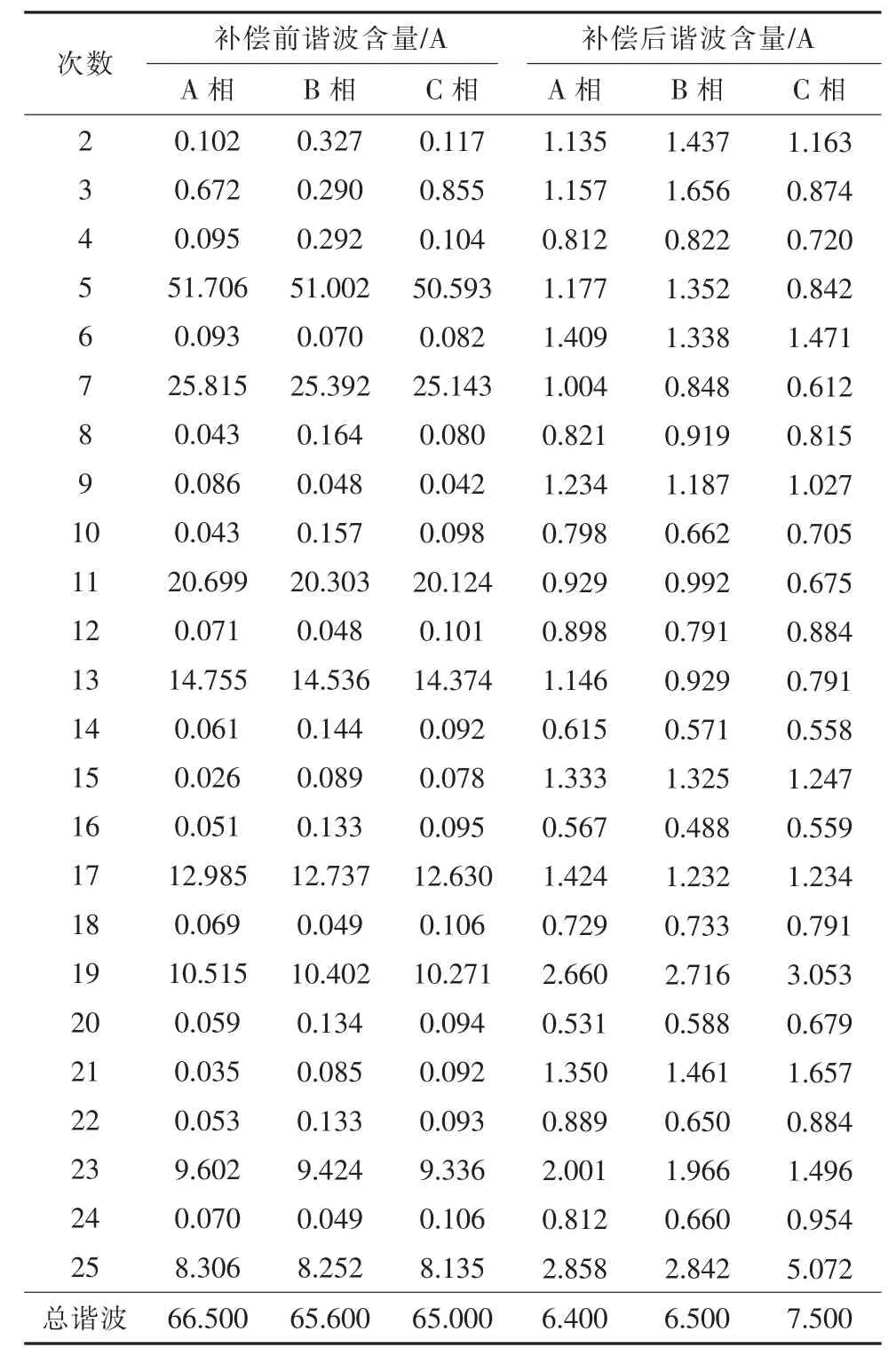
表1 总谐波补偿实验数据
4 结语
本文定量建立有源电力滤波器的电流环控制系统模型,分析对比多种已知控制方法的特点。在此基础上,提出一种基于指令修正的单比例谐振调节器有源电力滤波器控制方法,每个控制周期采样负载电流和有源电力滤波器输出电流,按照工频周期计算两者的幅值偏差和相位偏差,并使用上述偏差对每个控制周期的电流环指令进行修正,从而提高最终的谐波补偿精度。最后,通过在实际有源电力滤波器上进行的各次谐波及总谐波补偿实验,分析波形和计算数据,验证所提出控制方法的有效性。
