车辆制动盘模态耦合系统不稳定性研究
2021-07-16刘方平何冬康贺晓华
刘方平,苏 磊,何冬康,贺晓华
(柳州职业技术学院机电工程学院, 广西 柳州 545006)
车辆制动盘系统制动过程具有尖叫声频率高、噪声强度大等问题,难以进行有效控制.制动盘尖叫严重影响人的听觉舒适性,一直是汽车工业领域的技术难题和研究重点,业界对制动盘摩擦噪声产生机理开展了长期研究,以寻求有效降低摩擦噪声的控制措施[1-4];文献[5]提出的模态耦合理论将摩擦力或系统结构参数引入模态耦合系统,认为系统矩阵不对称引起系统的不稳定,最终产生振动噪声;文献[6-7]研究摩擦振动系统结构参数对模态耦合系统不稳定性的影响,为识别摩擦振动不稳定的摩擦副模态来源提供了理论依据,但研究主要集中在系统自身结构参数对系统不稳定性的影响,未考虑结合面形貌参数;文献[8-10]研究表明,制动盘结合面形貌特性对振动噪声的产生与否及频率高低有重要影响;文献[10-11]以车辆制动盘为对象,考虑微观接触形貌特性对宏观系统影响,建立两自由度摩擦振动系统,研究结合面切向与法向的刚度比、摩擦因数和固有频率比对系统稳定和不稳定区的影响及系统出现不同频率噪声的条件,研究结果表明,形貌参数是结合面产生振动噪声的主要影响因素;文献[11-12]认为两个摩擦副间存在摩擦时,由于摩擦力作用导致摩擦副位置倾斜,从而存在倾斜角度,但相关研究未考虑倾斜角度对模态耦合系统不稳定性的影响.
本文以车辆制动盘为研究对象,基于前人提出的车辆制动盘模态耦合模型,并在文献[12]关于结合面形貌特性对模态耦合系统不稳定性影响研究的基础上,考虑摩擦副倾斜角度,分析结合面形貌特性对系统不稳定性的影响.研究结合面切向与法向的接触刚度比、摩擦因数以及两者间的耦合效应和摩擦副倾斜角度及角度比对制动盘模态耦合系统不稳定性的影响.通过分析获取摩擦副倾斜角度、结合面接触刚度和摩擦因数以及相互间的耦合效应与高频噪声、低频颤振的关系.
1 车辆制动盘模态耦合模型
车辆制动盘系统由多个部分构成,在建立模态耦合模型时,为了便于计算及着重研究结合面切向与法向的接触刚度比、摩擦因数及摩擦副位置倾斜角度比对模态耦合系统的影响,需要进行一定的简化.
基于文献[5]提出的车辆制动盘模态耦合模型,不考虑结合面切向及法向阻尼,建立含有结合面形貌特性的两自由度摩擦振动系统,如图1所示.图1中:m为含有x和y两个自由度的集中质点质量;k1、k2分别为两根线性弹簧的刚度系数;θ1、θ2分别为两根线性弹簧与x轴的夹角,取值范围均为[0,π];kt、kn分别为m与移动平面的切向和法向刚度;v为m与移动平面的切向相对速度;Fn为施加的法向力;Ff为摩擦力.

图1 车辆制动盘的模态耦合模型
由图1所示的车辆制动盘两自由度模态耦合模型,可建立其动力学方程:
(1)
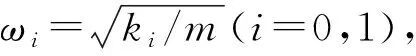
(2)


对车辆制动盘模态耦合系统进行稳定性分析时,由复模态理论可知,当矩阵A的特征值实部全部小于或等于0时系统稳定,否则系统不稳定.因此,可通过矩阵A讨论结合面形貌参数对系统稳定性的影响.
2 结合面特性参数对系统稳定性的影响
讨论结合面切向与法向的接触刚度比、摩擦因数以及两者间的耦合效应对车辆制动盘模态耦合系统不稳定性的影响.系统参数选取为:m=1 kg;ω1=2 000π rad/s;ω2=1 500π rad/s;kn=4×108N/m.[11]由于本节不讨论摩擦副位置倾斜角度比对系统的影响,因此取θ1=0.6π、θ2=0.8π.
2.1 结合面刚度比的影响
分别取结合面切向与法向的接触刚度比κ为0.6、0.65、0.7、0.75和0.8,求解矩阵A可得到如图2和图3所示特征值实部及固有频率与摩擦因数μ的关系.图2表明,随着μ不断增大,特征值实部出现分岔现象,系统进入不稳定状态,分岔所对应的临界摩擦因数点称为Hopf分岔点.以结合面切向与法向的接触刚度比κ为参变量,随着κ的增大,Hopf分岔点逐渐前移,对应于图3耦合频率亦前移且不断增大,系统提前进入不稳定状态.此外,综合图2和图3也可发现,κ小于0.6时,无论μ取何值系统均处在稳定状态.
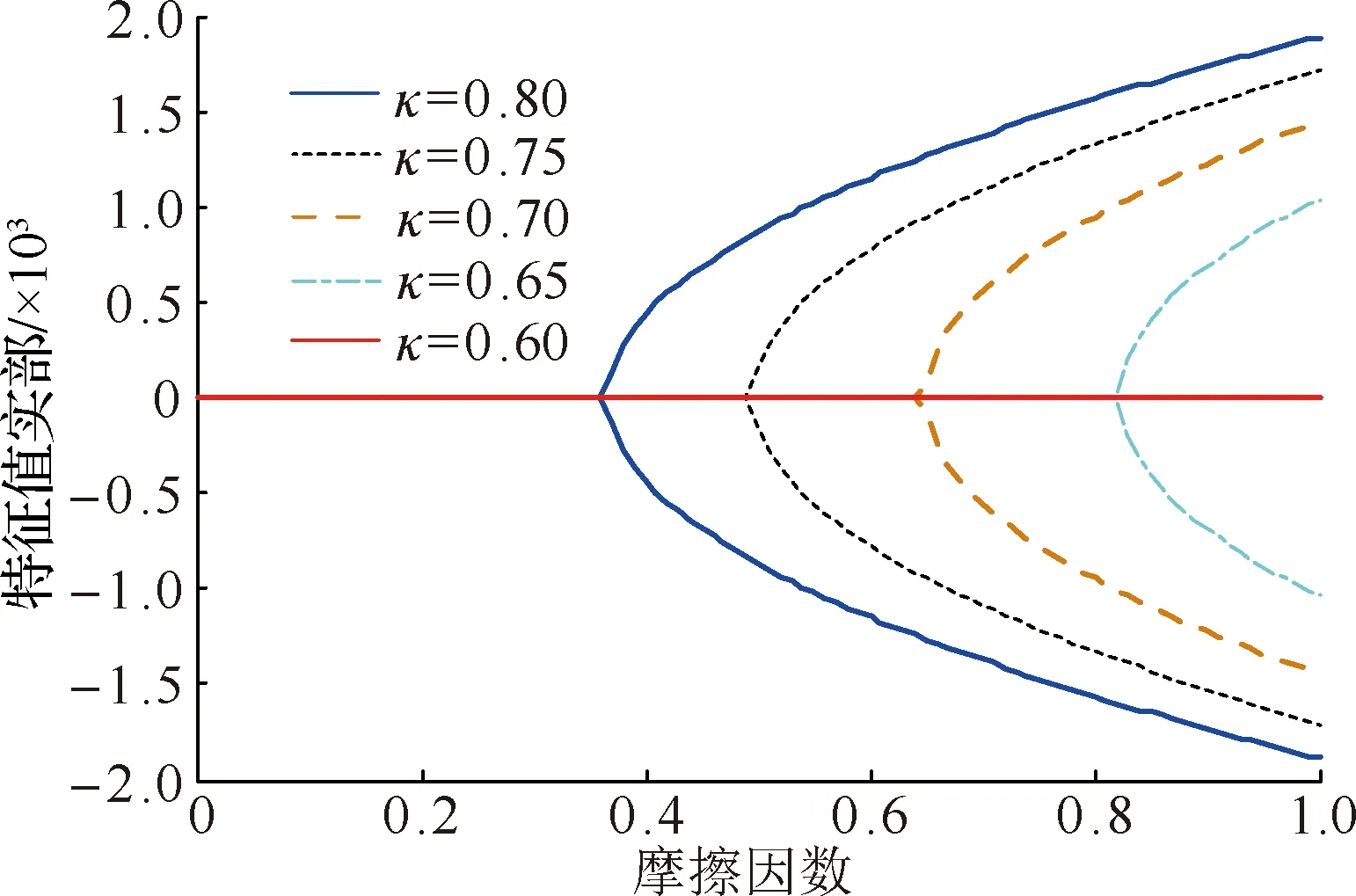
图2 特征值实部与摩擦因数的关系
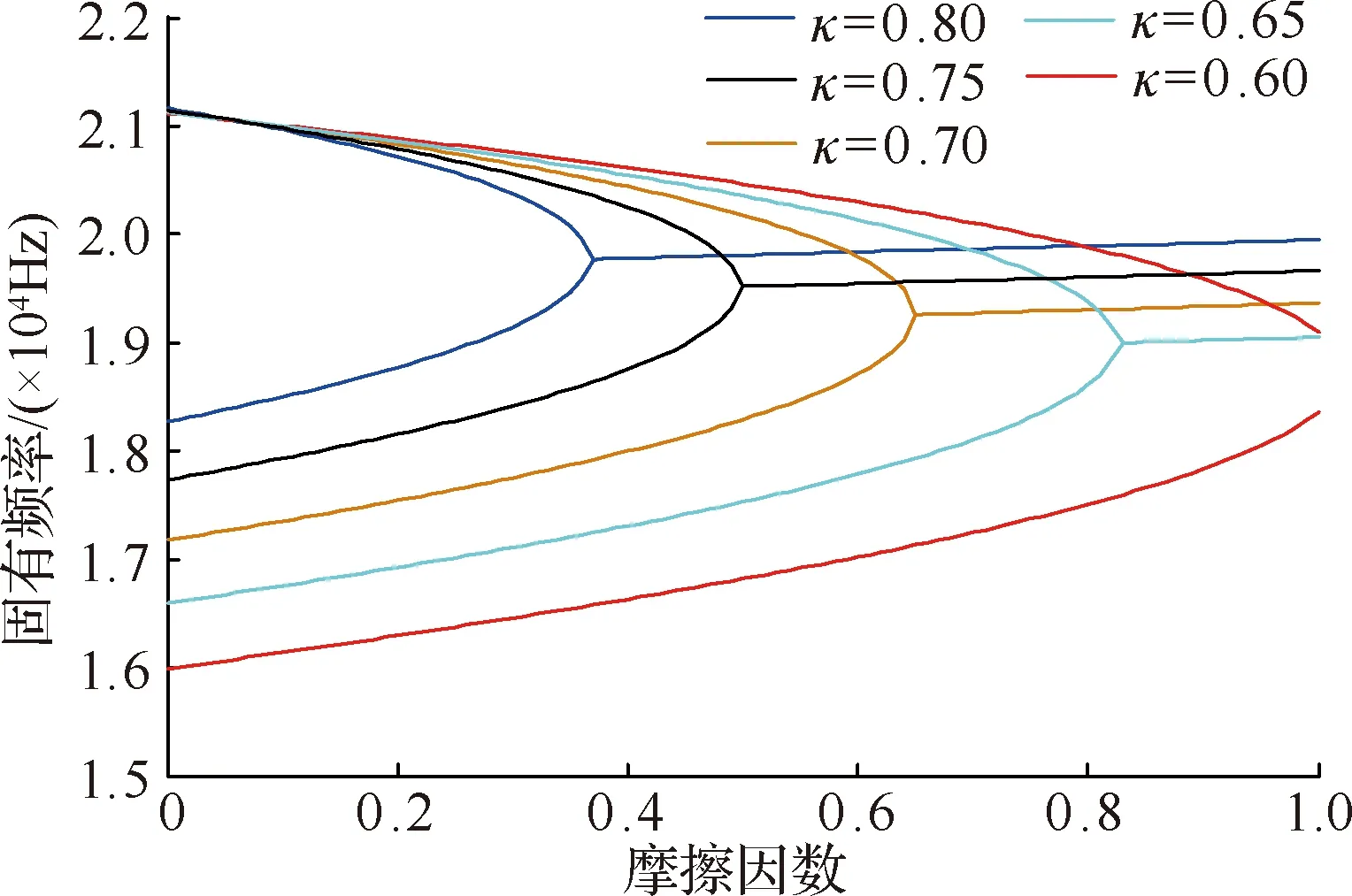
图3 固有频率与摩擦因数的关系
2.2 结合面摩擦因数的影响
摩擦因数μ分别取0.05、0.1、0.15、0.2和0.25,求解矩阵A得到如图4及图5所示的特征值实部、固有频率与结合面刚度比κ的关系.图4和图5表明:在同一摩擦因数下,随着κ的增大,特征值实部分岔及频率耦合现象开始出现,系统进入不稳定区;当摩擦因数μ在增大时,Hopf分岔点逐渐滞后,至μ=0.25后特征值实部分岔现象消失,且不存在耦合频率,系统进入稳定状态;相较于二阶固有频率,一阶固有频率随κ的取值加大而显著增大.
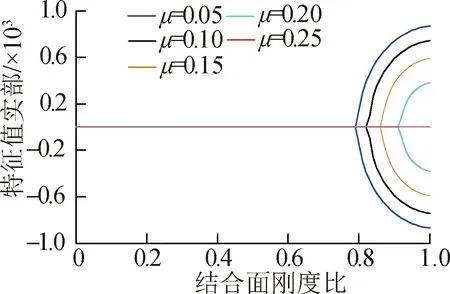
图4 特征值实部与结合面刚度比的关系

图5 固有频率与结合面刚度比的关系
2.3 结合面刚度比与摩擦因数共同影响
讨论结合面刚度比κ、摩擦因数μ对系统不稳定性的共同影响.以κ和μ为变量,求解矩阵A得到如图6和图7所示的特征值及固有频率与结合面刚度和摩擦因数的三维关系.
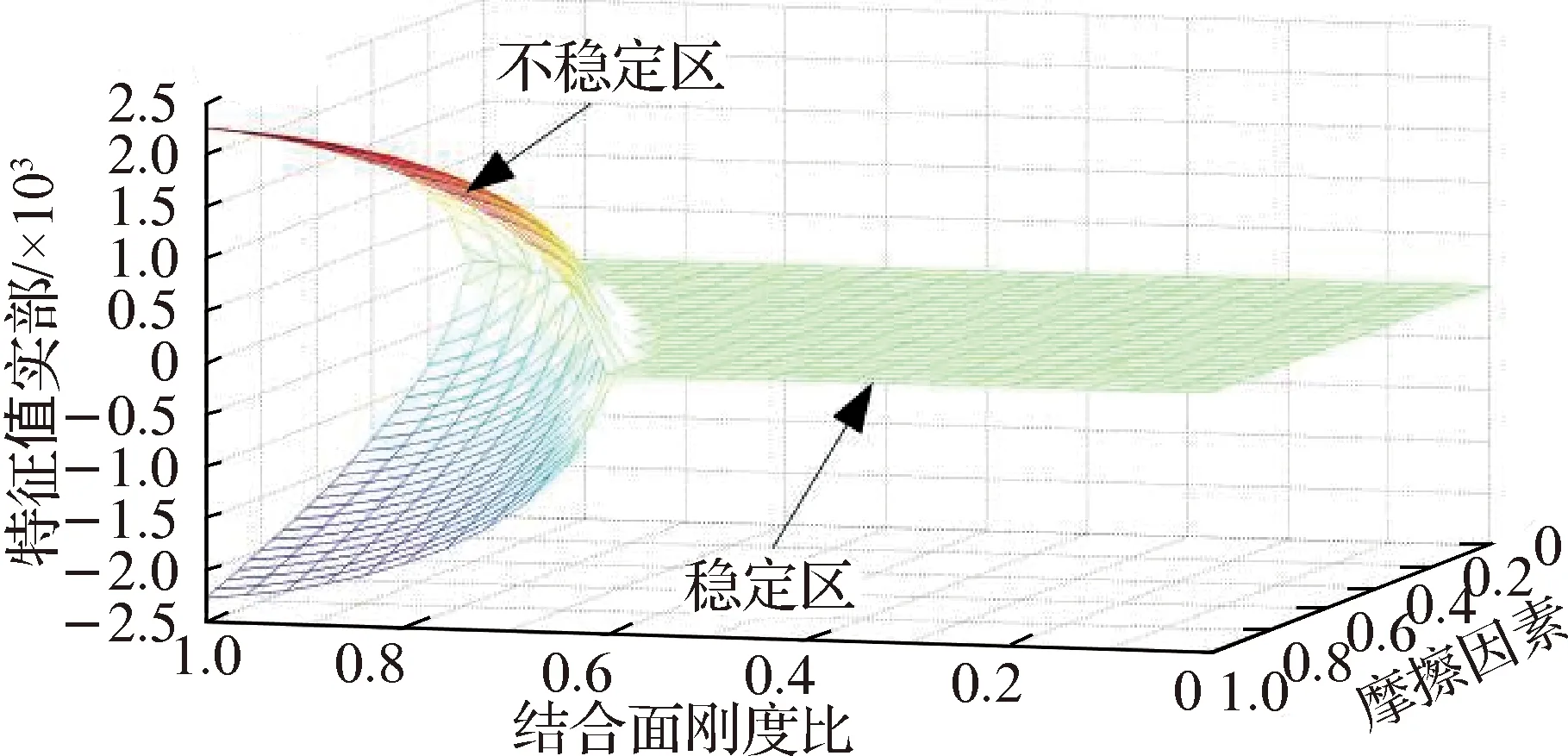
图6 特征值实部与结合面刚度比和摩擦因数的关系
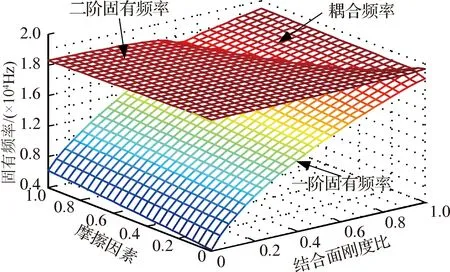
图7 固有频率与结合面刚度比和摩擦因数的关系
图6表明,结合面刚度比κ和摩擦因数μ均对系统不稳定性具有显著影响,二者都趋近于1时,特征值实部出现分岔,系统进入不稳定区,可能产生摩擦噪声;μ的增大使得Hopf分岔点提前,而κ的增大则使得Hopf分岔点滞后;当二者都趋近于0时,系统处在稳定区.图7表明,κ接近于1时,μ微小增加便会出现频率耦合,使系统进入不稳定区;反之,当κ接近于0时,无论μ取任何值,均未出现耦合频率,即系统一直处于稳定区.综合图6和图7不难发现,相对于μ,κ对系统不稳定性影响更显著.
3 摩擦副位置倾斜角度对系统稳定性的影响
两个摩擦副间存在摩擦时,会由于摩擦力作用导致摩擦副位置倾斜[12],即存在摩擦副倾斜角θ1和θ2.结合κ和μ讨论摩擦副位置倾斜角度对系统不稳定性的影响.系统参数选取为:m=1 kg;ω1=2 000π rad/s;ω2=1 500π rad/s;kn=4×108N/m.
3.1 摩擦副位置倾斜角度比的影响
根据结合面刚度比κ与摩擦因数μ对模态耦合系统稳定性共同影响分析可知,当κ和μ均趋近于1时,系统进入不稳定区.为了研究摩擦副位置倾斜角度比的影响,κ与μ分别取不同值求解矩阵A.图8、图9分别为κ和μ取不同值时对应的特征值实部、固有频率与摩擦副倾斜角度θ2和摩擦副倾斜角度比γ的关系.
图8表明,θ2和γ对矩阵A的特征值实部都具有显著影响,二者都趋近于1时不稳定区范围增大;随着κ和μ取值变小,不稳定区及特征值实部均逐渐变小,至κ=0.3和μ=0.3时,系统均处于稳定区;若κ=0.9和μ=0.9,且θ2接近于1,特征值实部随着γ的变化经历分岔—合并—分岔的过程,不稳定区占多数.
由图9可见:与特征值实部变化类似,θ2和γ均趋近于1时,出现耦合频率;随着κ和μ减小,耦合频率范围变小且耦合频率值也在变小,不稳定噪声产生概率可能会减小;当κ=0.3和μ=0.3甚至更小时,不管θ2与γ取何值,一阶和二阶固有频率完全分开,不会出现耦合频率,系统稳定.此外,综合图8、图9表明,θ2与γ均接近于0时,系统处于稳定状态.
3.2 倾斜角度比与结合面刚度比的共同影响
以摩擦副位置倾斜角度比γ与结合面刚度比κ为系统变量,其余为参变量,对摩擦因数μ和摩擦副倾斜角度θ2分别取不同值求解矩阵A.图10、图11分别为μ和θ2取不同值时对应的特征值实部、固有频率与κ和γ的关系.
图10表明,μ和θ2取值增大,则特征值实部分岔区域变大,即不稳定区域范围扩大;μ=0.9和θ2=π时,κ增大使得Hopf分岔点提前,系统更早进入不稳定区,而γ在[0,0.75]范围内增大使得Hopf分岔点提前,γ在[0.75,1]范围内增大则使得Hopf分岔点滞后;μ=0.6和θ2=0.7π时,特征值实部出现两次分岔,系统存在两个不稳定区,当κ趋近于1时,特征值实部随γ经历分岔—合并—分岔的过程;当μ=0.3和θ2=0.4π甚至更小时,特征值实部全为0,系统处于稳定状态.
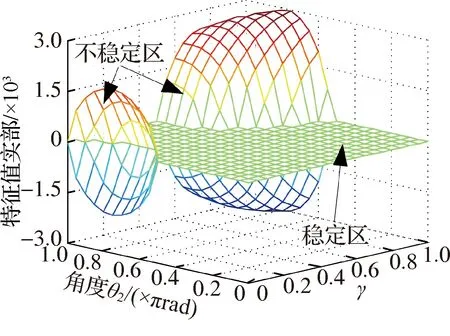
(a) κ=0.9,μ=0.9
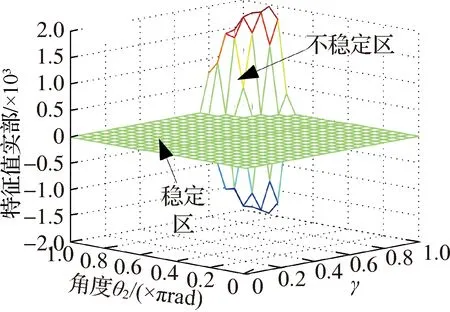
(b) κ=0.6,μ=0.6
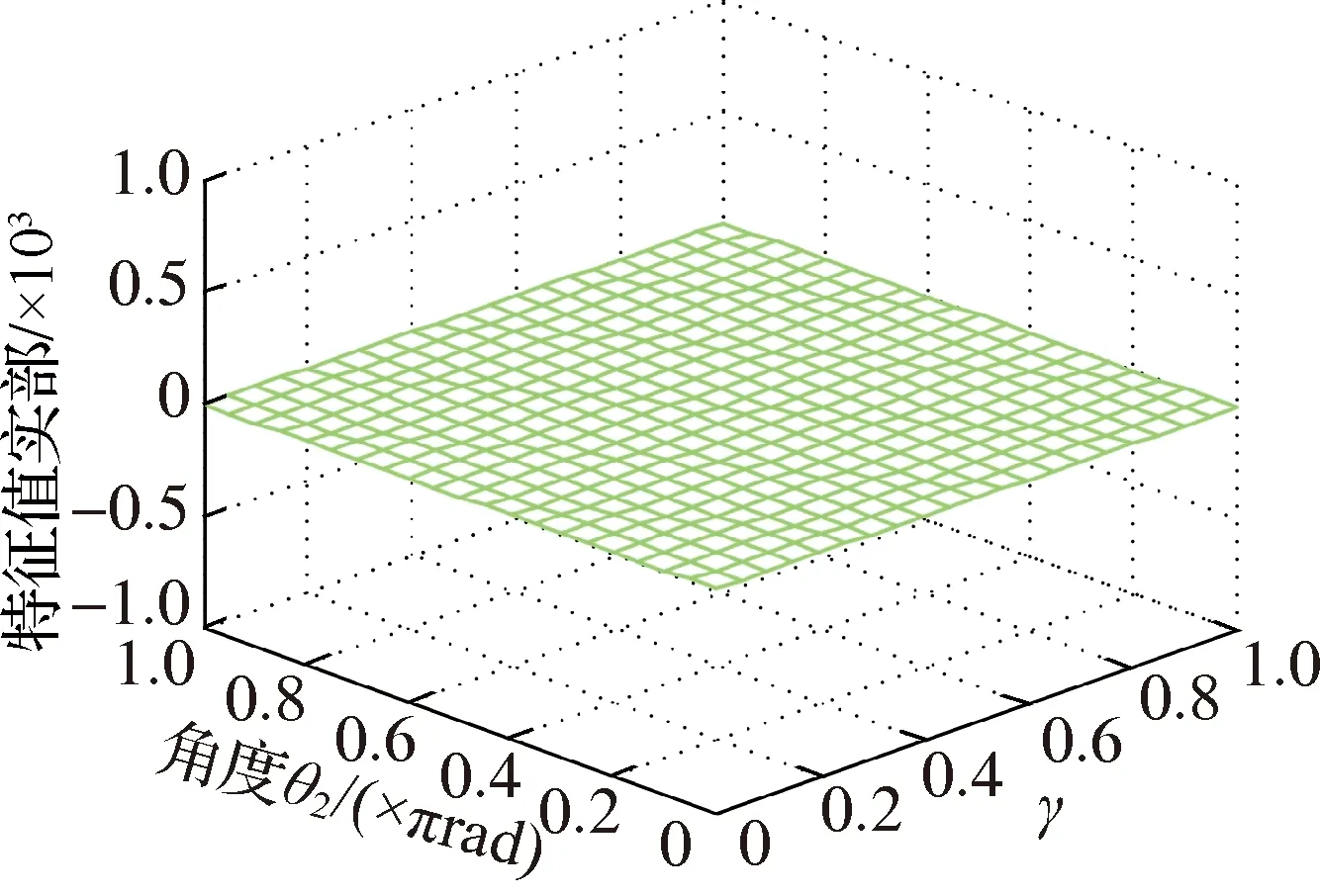
(c) κ=0.3,μ=0.3
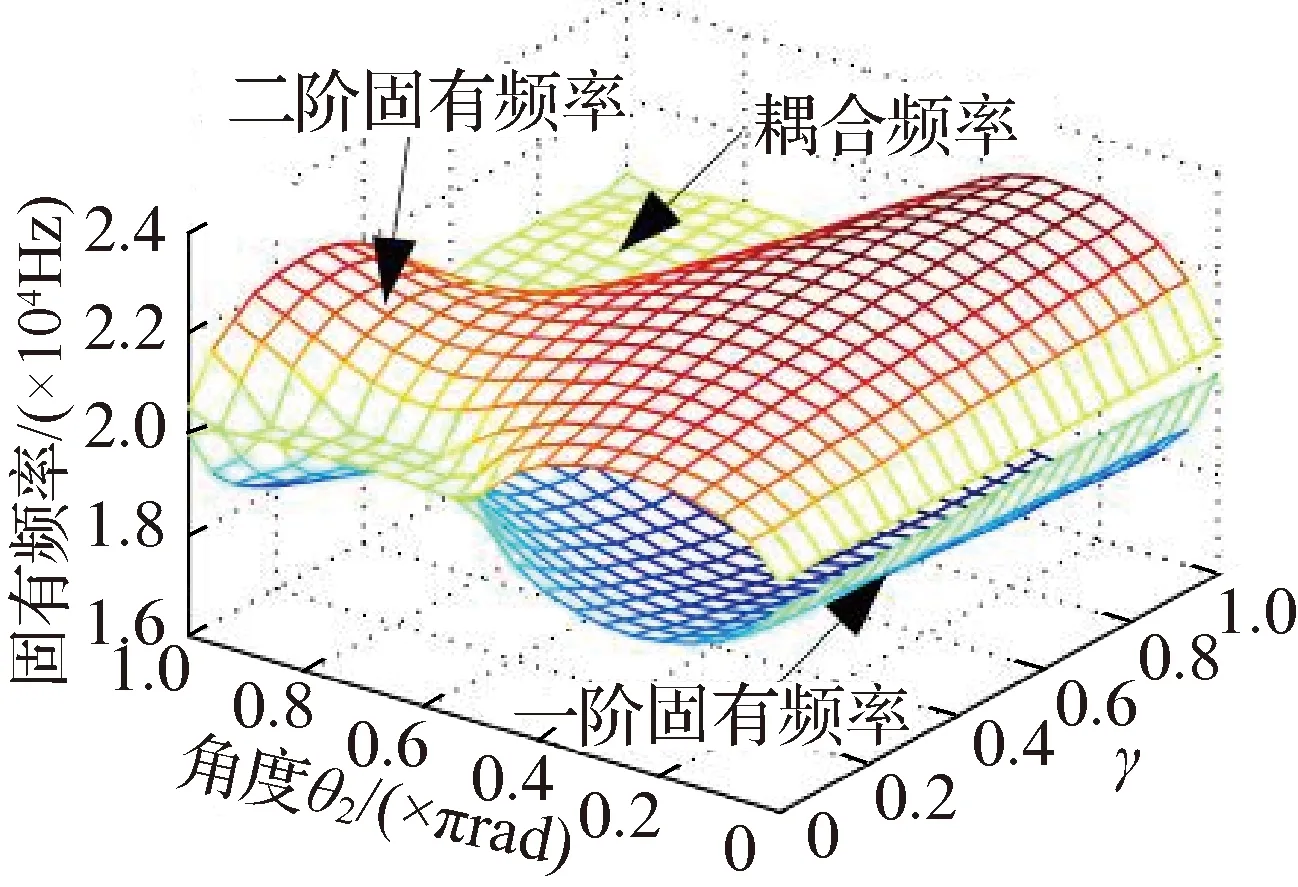
(a) κ=0.9,μ=0.9
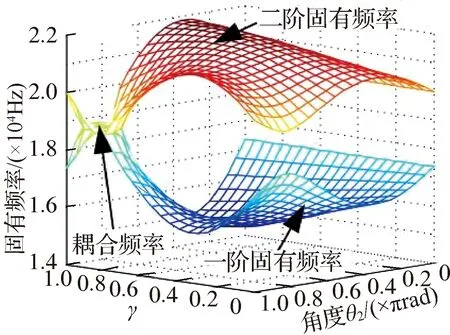
(b) κ=0.6,μ=0.6

(c) κ=0.3,μ=0.3
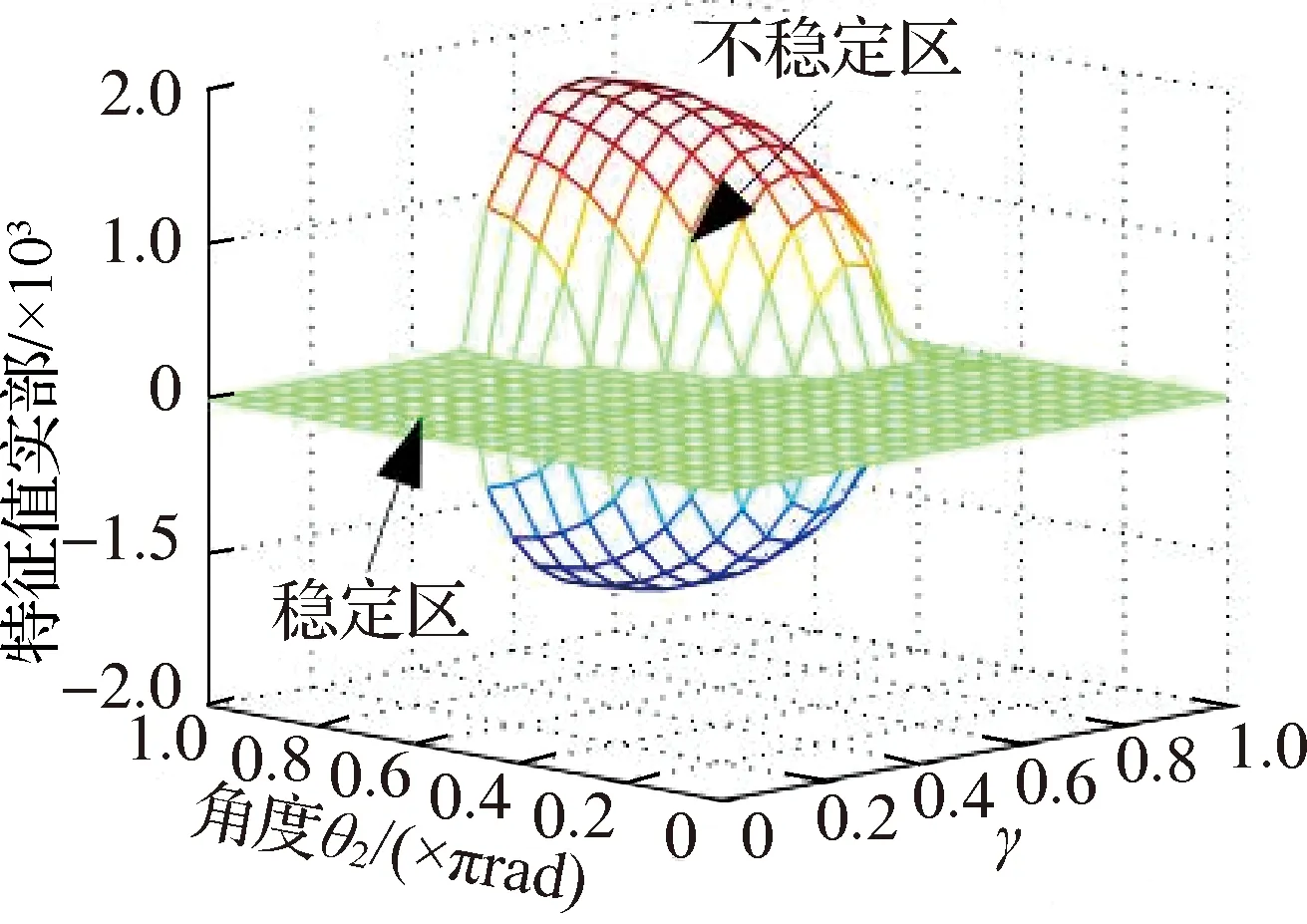
(a) μ=0.9,θ2=π
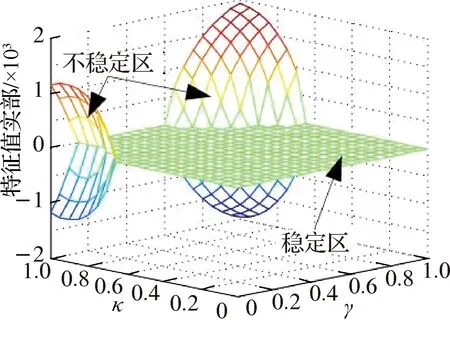
(b) μ=0.6,θ2=0.7π
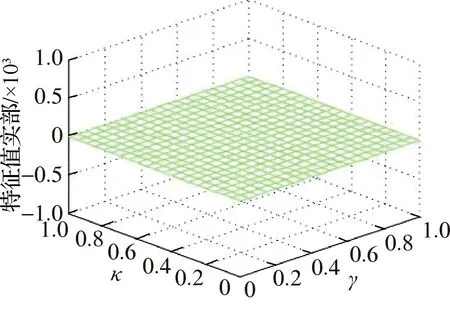
(c) μ=0.3,θ2=0.4π
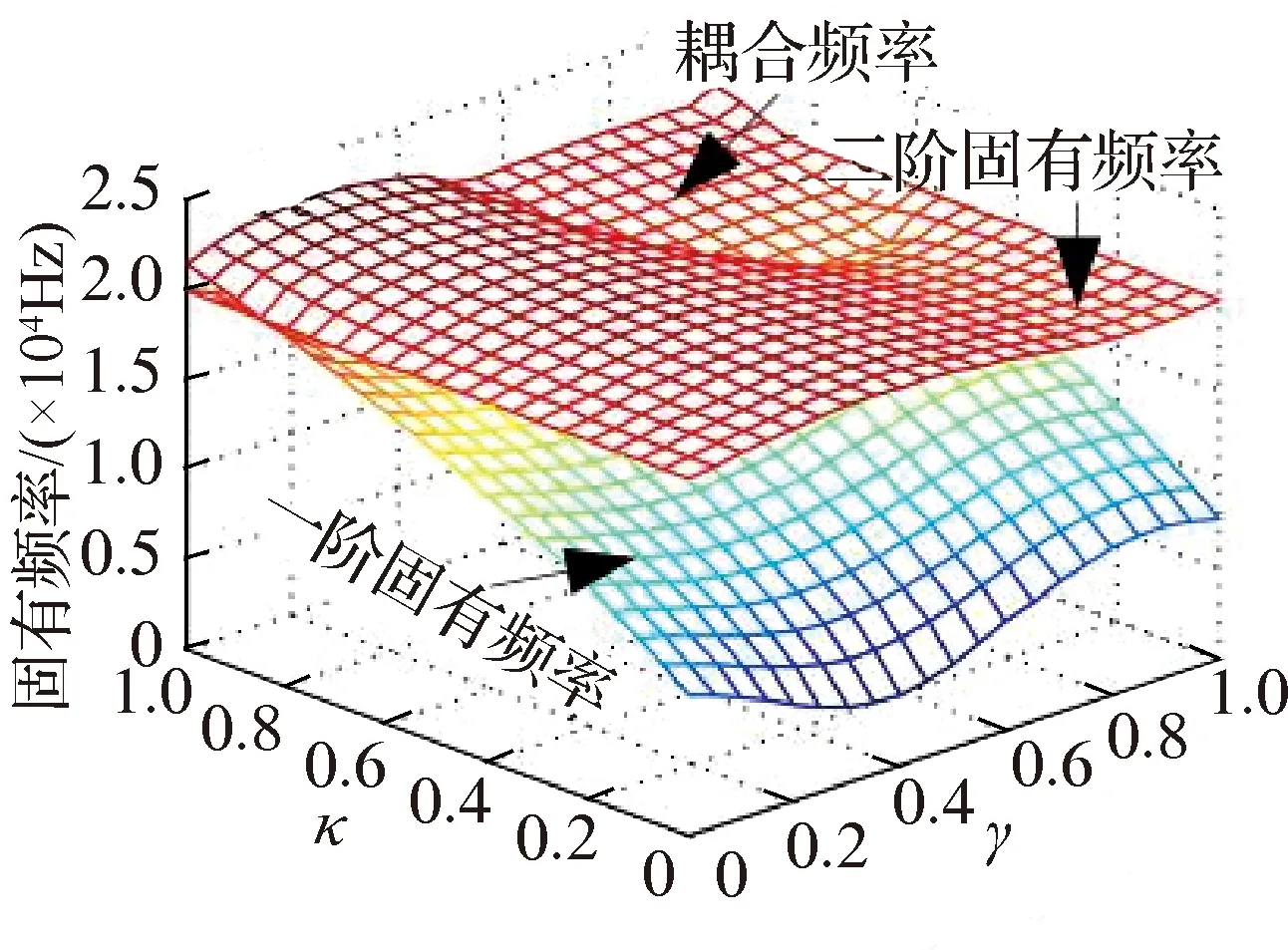
(a) μ=0.9,θ2=π
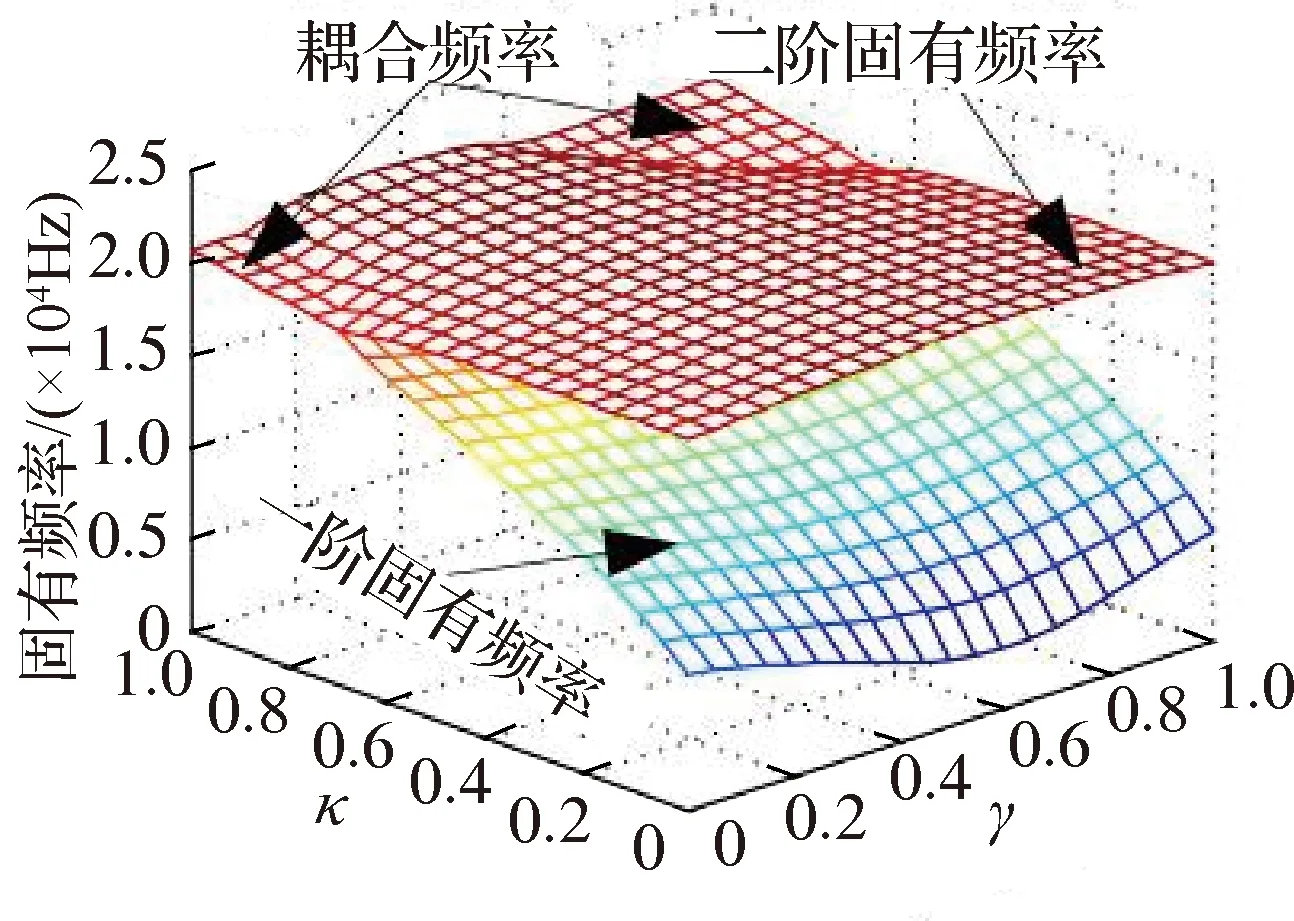
(b) μ=0.6,θ2=0.7π
(c) μ=0.3,θ2=0.4π
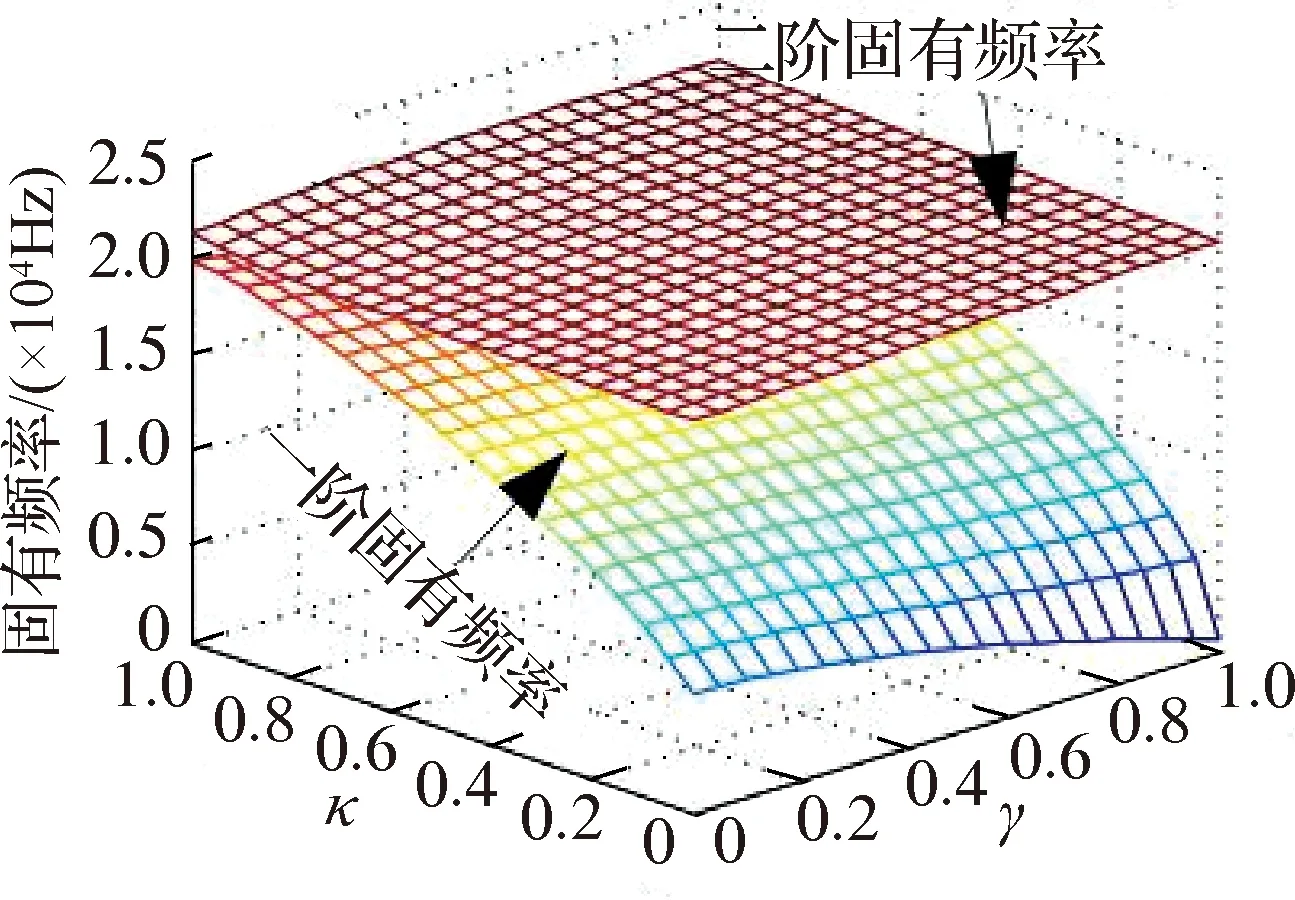
图11表明,一阶固有频率随着κ和γ取值不同存在显著变化,而二阶固有频率的变化则不明显;随着μ和θ2的减小,耦合频率范围及其值都减小,当μ=0.3和θ2=0.4π甚至更小时,一阶和二阶固有频率完全分开,不存在耦合频率,系统处于稳定区;相较于γ,κ对一阶固有频率的影响较明显,随着κ的增大一阶固有频率也增大.
3.3 倾斜角度比与摩擦因素的共同影响
以γ和μ为系统变量,其余为参变量,讨论二者对系统不稳定性的影响.对κ和θ2分别取不同值求解矩阵A.图12、图13分别为κ和θ2取不同值时对应的特征值实部、固有频率与γ和μ的关系.
图12、图13表明,κ和θ2对系统不稳定性有重要影响,随着二者取值的减小系统不稳定区域急剧变小,至κ=0.3和θ2=0.4π时,特征值实部为0,一阶和二阶固有频率完全分开,系统处于稳定区;当κ和θ2趋近于最大值(如κ=0.9和θ2=π)时,固定γ并以μ为变量,随着μ的增大,特征值实部Hopf分岔点逐渐提前,系统更早进入不稳定区,固定μ并以γ为变量,随着γ的增大且趋近于1,Hopf分岔点先提前再滞后;μ和γ对一阶和二阶固有频率的影响类似,使得二者对称于耦合频率.综合图12、图13可发现,γ取值较大时,系统基本处于不稳定区,而γ和μ都接近于0时,系统都处于稳定区,摩擦噪声发生概率较小.
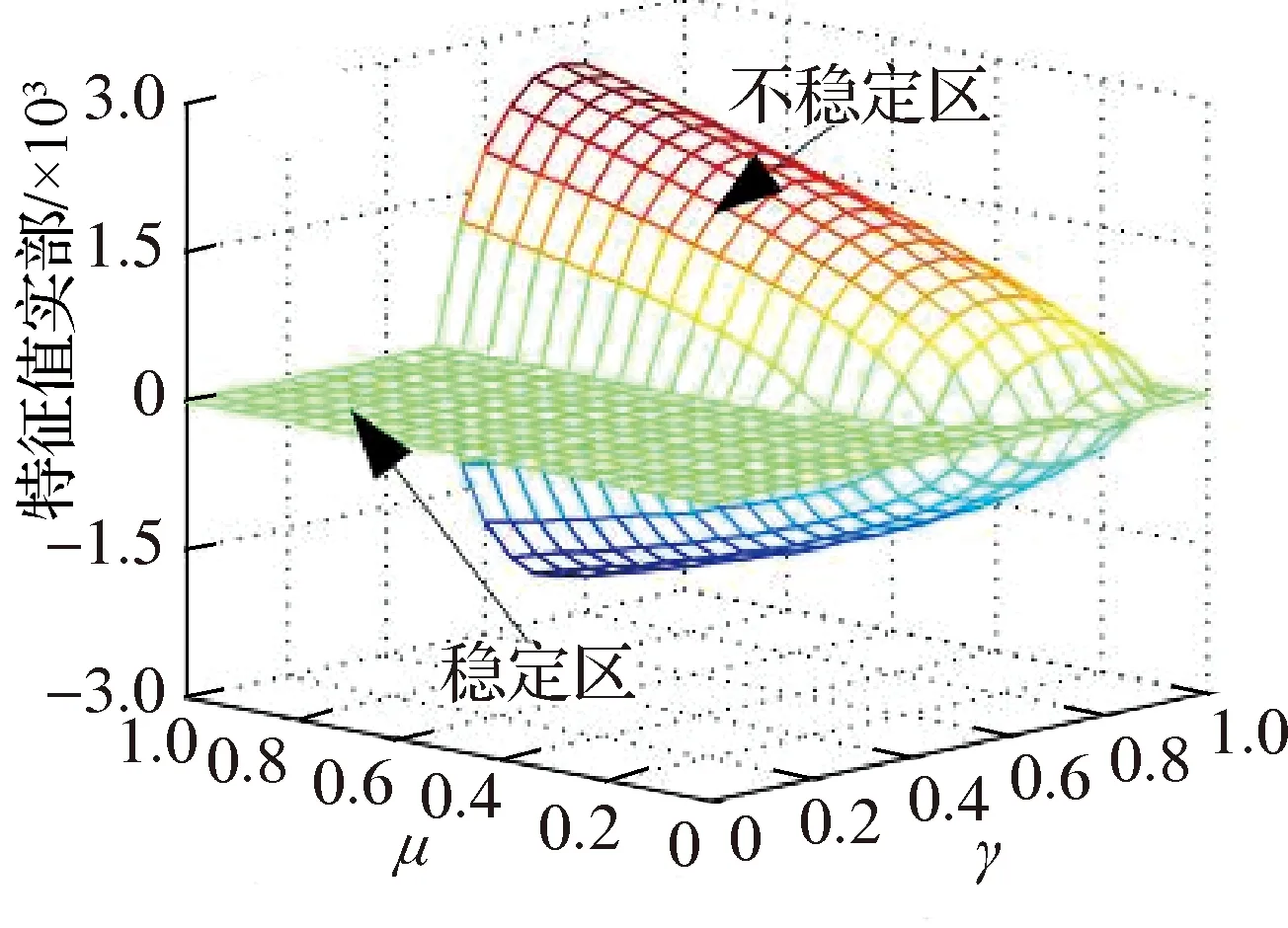
(a) κ=0.9,θ2=π

(b) κ=0.6,θ2=0.7π
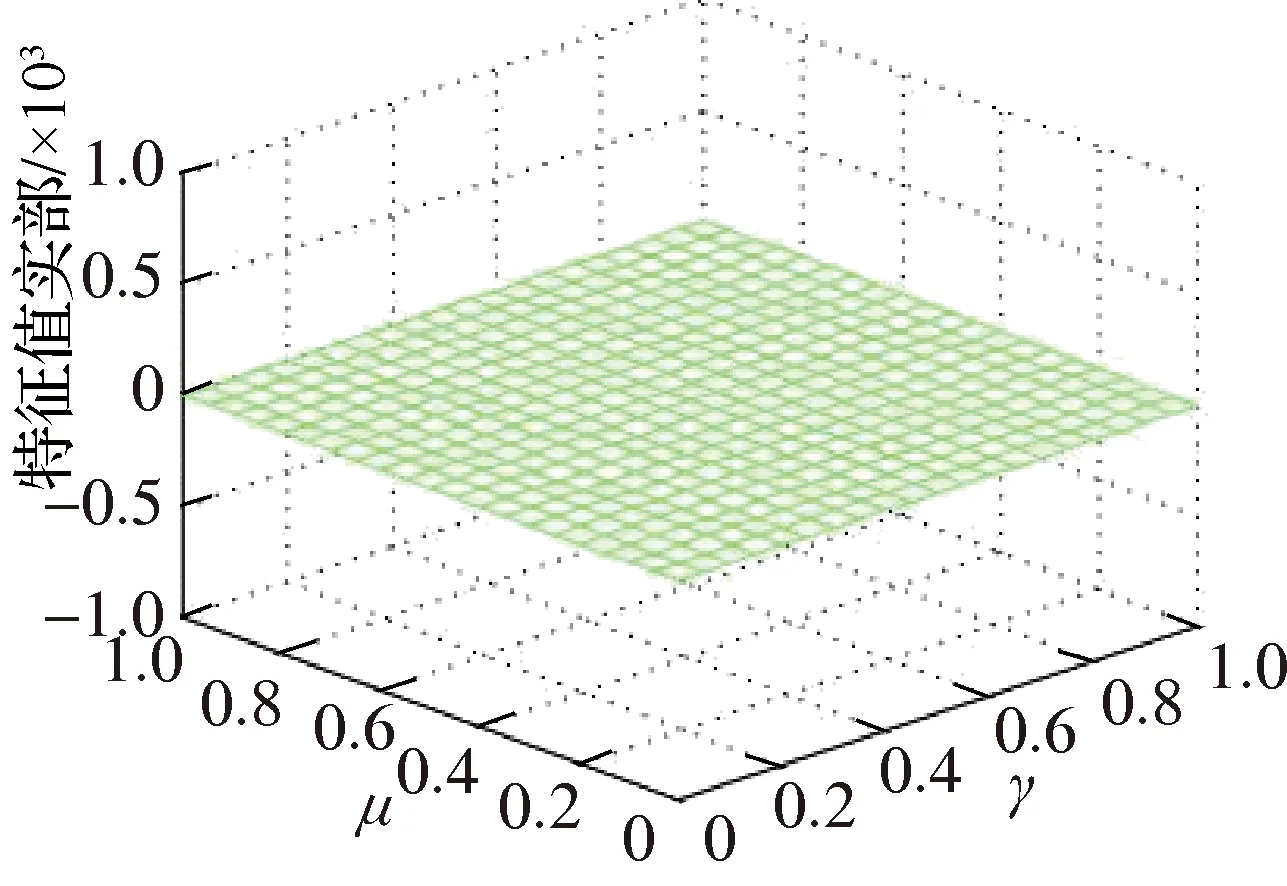
(c) κ=0.3,θ2=0.4π

(a) κ=0.9,θ2=π

(b) κ=0.6,θ2=0.7π
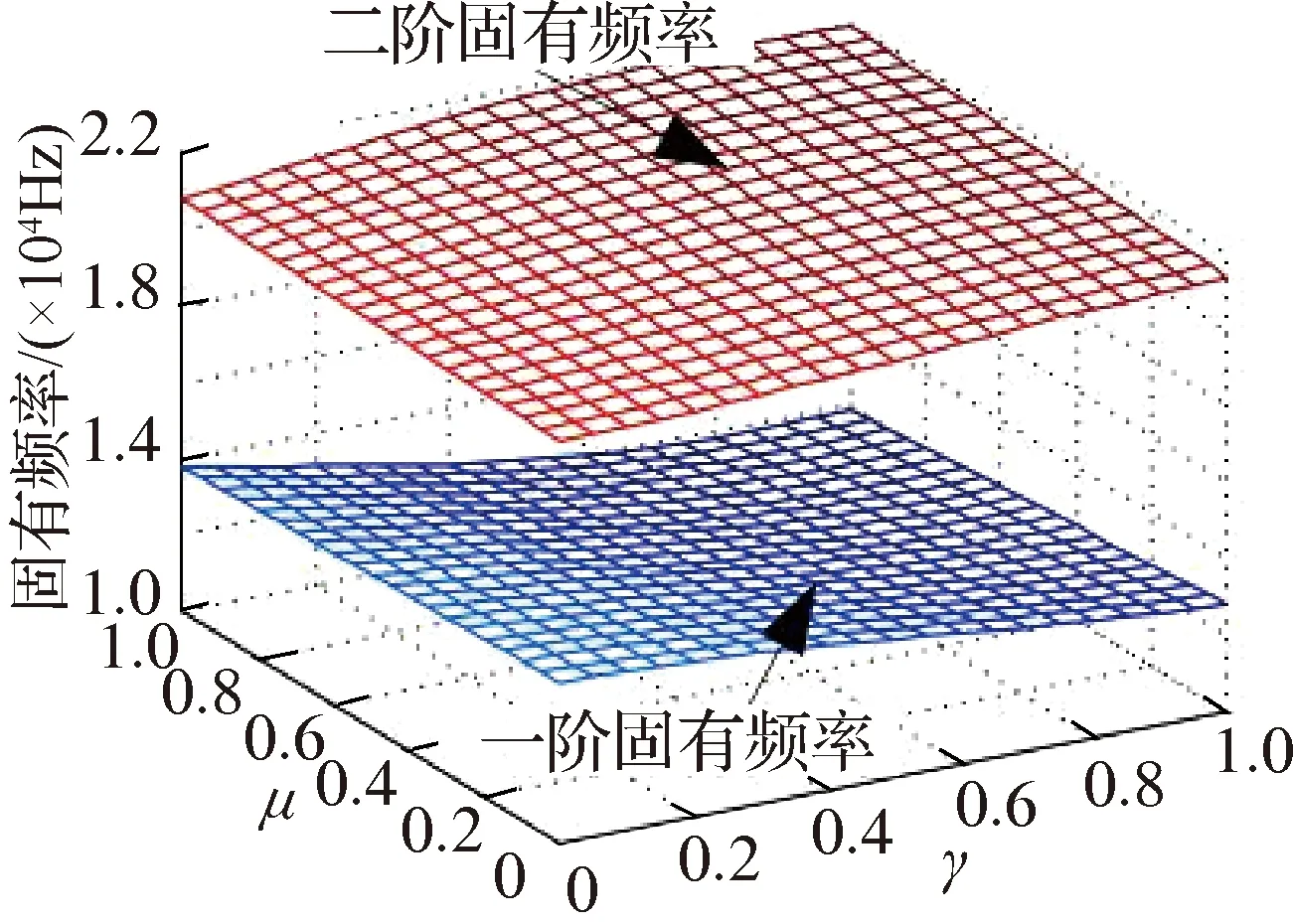
(c) κ=0.3,θ2=0.4π
4 结语
基于分形接触刚度对车辆制动盘系统建立了含有两自由度的典型模态耦合模型,研究了结合面切向与法向的接触刚度比、摩擦因数以及两者间的耦合效应对制动盘模态耦合系统不稳定性的影响,并着重研究了摩擦副倾斜角度及角度比对制动盘模态耦合系统不稳定性的影响,可为后续制动器制动性能理论研究提供有益参考.
