水下机器人控制系统设计与仿真

韩 林,施昕昕

(南京工程学院自动化学院, 江苏 南京 211167)

随着人类科技的发展和陆地资源的日益减少,人类开始开发拥有无尽资源的海洋[1],因此需要具有高度稳定性和灵活性的有缆水下机器人(remote operated vehicle,ROV)在浅水区进行水下信息采集[2].这种小型机器人需要装载照明、摄像、声纳等观测设备,监测河堤、大坝水况,收集河道桥墩的水下信息,检修近海码头港口和船舶外体,并在渔业养殖和救援打捞等一些领域有着广泛应用[3].水下环境复杂且危险,采用滑模控制器比传统滑模控制器更加能够保证ROV维持预设航向和预设深度,稳定地完成水下作业[4-5].水下机器人对运动控制器要求高,同时要求具有通信、采集信息等功能[6].保持及调整航向和下潜深度是ROV在水下稳定作业的基本要求之一[7].PID控制和鲁棒控制、自适应控制、模糊控制的主要区别在于PID控制是基于反馈的一种控制方式[8],其控制方式简单且在水下适应性好[9],但响应时间较长.PID控制过程包括获取输入数据、将输入值与期望值进行比较得到相应的偏差[10]、消除偏差使系统进入稳定状态[11].水下环境复杂多变,不能获得精确的系统模型[12],而滑模控制可以较好克服系统的不确定性,并具有很强的鲁棒性,可以较好控制非线性系统[13],将它应用于水下机器人控制可以获得较好的效果.滑模控制最大的问题是到达滑模平衡点后上下滑动,这种往复的滑动导致抖颤,会严重影响滑模控制的控制效果,克服抖颤成为滑模技术的一大研究方向[14].有效消除抖颤的难点是系统控制器的输出具有抖动,输出值最终会在期望值附近来回穿梭.本文设计一种基于滑模控制的有缆水下机器人控制系统,并对其艏向控制和深度控制进行仿真.

1 ROV结构

本设计为一种小型潜水式ROV,其中包括用来检测深度的深度传感器和用来检测姿态的姿态传感器.通过在岸上的控制台向脐带缆发命令控制ROV前进后退、上浮下潜、左右转动.图1为ROV的整体构造图,以3块3 mm厚铝板作为机身主体机械结构框架,用法兰将水下摄影台半球罩和有机玻璃管紧密固定组成密封电子舱,再用支架固定在底板上.在ROV左右两边用支架固定控制ROV上升或下潜的垂直驱动器,在ROV底部放置4个控制ROV前进、后退、左旋、右旋的水平驱动器.由ROV样机测得运动坐标系原点O到水平驱动器的垂直距离和垂直驱动器到z轴距离,ROV质量约为10 kg,将相关参数输入到系统参数中进行Simulink仿真建模.ROV控制系统模块图如图2所示.

图1 ROV构造图

图2 ROV控制系统模块图

2 ROV动力学建模分析

图3 水下机器人运动坐标系

η0=[xByBzBφBθBψB]T

(1)

定义六自由度线速度/角速度向量为:

v=[uvwpqr]T

(2)

由于本设计ROV外形对称,可以认为ROV的浮力和重力能够保持平衡状态,且ROV在水平面运动过程满足:z=0,φ=0,θ=0,w=0,p=0,q=0.ROV在垂直面运动过程满足:y=0,φ=0,ψ=0,v=0,p=0,r=0.

通过对ROV系统受力进行分析,可得到其六自由度空间运动方程为:

Mv+C(v)v+D(v)v+g(η)+f=τp

(3)

式中:τp为水下机器人所受到的总推力;M为机器人系统惯性矩阵;g(η)为重力与浮力的恢复力矩阵;C(v)为机器人受到的科氏向心力矩阵;D(v)为水阻尼矩阵;f为ROV受到的缆力、洋流、机械手作业的反冲击力等外界干扰.

ROV水平面运动的三自由度运动学方程为:

(4)

ROV水平面运动的三自由度动力学方程为:

(5)

ROV垂直面运动的三自由度运动学方程为:

(6)

ROV垂直面运动的三自由度动力学方程为:

(7)

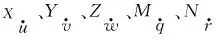
在理想情况下,ROV的重心和浮心重合,单个驱动器的推力可简化为:

(8)

式中:T为驱动力;ρ为水密度,淡水密度为ρ=998 kg/m3;n为螺旋桨转速r/s;Dp为螺旋桨直径,通过测量实际电机螺旋桨直径,取Dp=40 mm;KT为螺旋桨推力系数(淌水特性),实际情况下框架式机器人KT=0.7～0.9,取KT=0.8.

在理想情况下,ROV水平方向总的推力矩为:

M=4T0c=4KTρn2D4c

(9)

由于ROV 4个平面驱动器为面对背45°矢量布置,且推进器推力力矩系数c=cos 45°,故水平方向前进的最大推力理论值为:

T总=4T单cos 45°=2.83T单

(10)

ROV空间力和力矩计算公式为:

xN=(T1+T2+T3+T4)cosα

(11)

yN=(T1-T2-T3+T4)cosα

(12)

zN=T5+T6

(13)

ψN=c(T1-T2+T3-T4)sinα

(14)

3 ROV仿真模型

3.1 定向和深度控制器设计

3.1.1 定向控制器设计

因ROV的驱动器输出推力有最大值,故ROV的运动速度有固定的值,需要将定向时机器人的输出速度加以限定.当启动定向功能时,初始角度为0,定向扰动为一个上升沿的阶跃脉冲信号.当扰动值相对于原位置大于0的时候,反馈之后的数据小于0,偏差角度大于0.2 rad且偏差超过额定误差,则输出速度固定为-0.3 rad/s,否则速度为一个渐变值;偏差角度大于0.2 rad且偏差值相对于原值小于0,反馈后的数据便会大于0,超过偏差后,输出速度便会固定为0.3 rad/s,否则速度为一个渐变值.定向偏差角模块(见图4)与电机直接相连,在机器人出现偏转时直接控制电机旋转,让机器人实现定向功能.图5为定向滑模控制器滑模型,设计的模面为:

图4 定向偏差角模块模型

图5 定向滑模控制器模型

(15)

式中:ψ和ψx分别为航向角位置的测量值与设定值;e为测量值与设定值的差值e=ψ-ψx.

定向滑模控制方程为:

(16)

式中,T和K为调节参数.

通过调节参数T和K满足条件,使系统以适当速度到达切换面.

3.1.2 定深控制器设计

当ROV在水下某一个深度位置时,对其施加一个外力改变其深度位置,ROV通过深度传感器检测到所处深度位置发生变化回到原来的深度位置.图6为定深滑模控制器模型,设计的滑模面为:

图6 定深控制器模型

(17)

式中:z为ROV深度的测量值;zx为ROV深度设定值;e为测量值与设定值的差值e=z-zx.

定深滑模控制方程与定向滑模控制方程相同,参见式(16).

3.2 ROV仿真结果分析

表1 系统参数

对ROV进行受力分析并进行定向仿真建模,ROV在定向之后,无论如何运动,舰首都保持在一个方向上,不会发生改变.为确定定向功能,加入扰动变量.模拟加入浪涌,随着浪涌的增强,ROV出现偏转和摇晃的现象,但随即ROV马上恢复到原状态,舰首保持不变;给定相应偏航角角度扰动模拟浪涌,ROV出现偏航角偏转,但随着碰撞的消失,ROV恢复到原来的偏航角,舰首保持不变.ROV的位置为η0=[0 0 0 0 0 2]T,水流扰动为[2 2 2]T.给定ROV一个偏航扰动为0.3 rad的阶跃扰动干扰角度,ROV回到原来的偏航角位置后偏航角角速度变为0，见图7.图8显示当偏航扰动为0.3 rad时,ROV实现了反向0.3 rad的偏转角，又回到ROV原来所在的航向位置,实现了定向控制作用.通过滑模定向控制器和PID定向控制器对比,可以看出滑模定向控制器稳定性好,控制时间短、速度快.

图7 ROV偏航角角速度变化仿真图

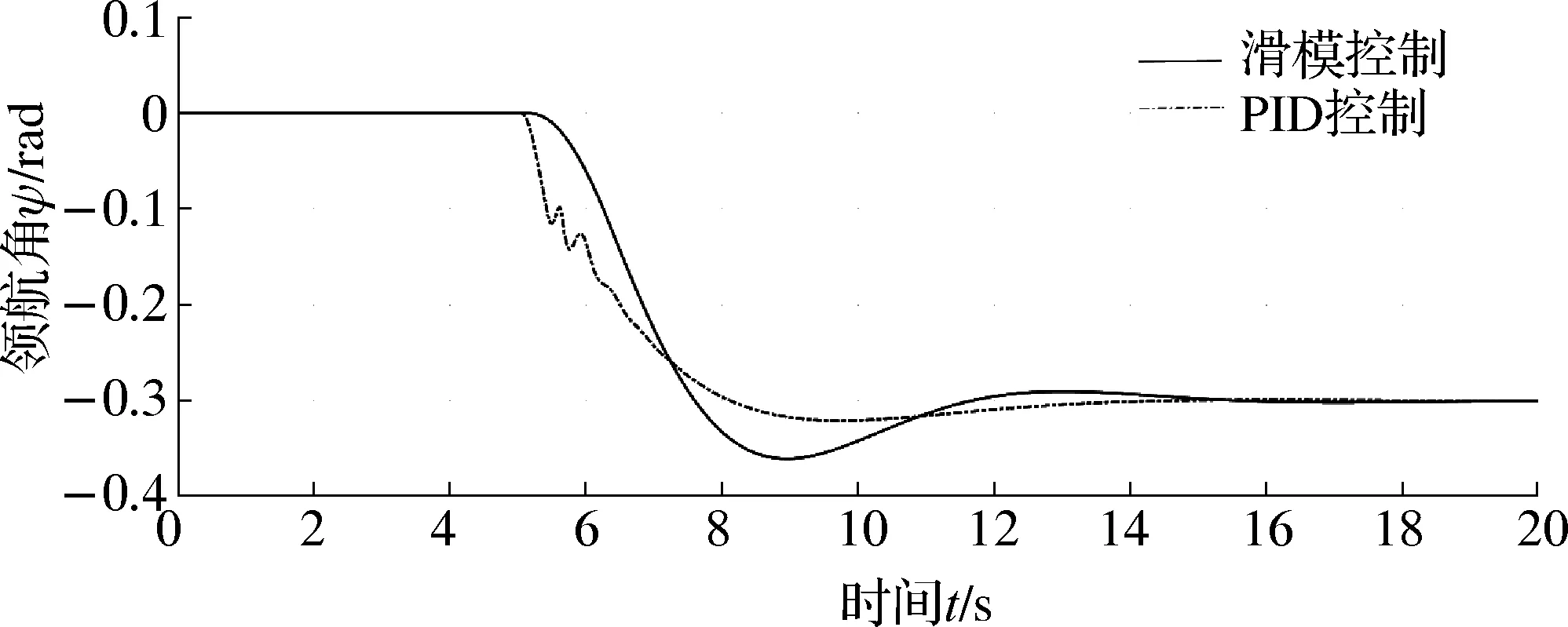
图8 ROV偏航角仿真变化图

对ROV进行受力分析并进行定深仿真建模,ROV位置为η0=[0 0 2 0 0 0]T,水流扰动为[2 2 2]T,给定ROV定深至4 m位置,加入一个模拟浪涌约10 N的垂直方向定深扰动,由图9可见,滑模控制中模拟量从0 m深度约2.5 s进入稳定状态,并且无超调,稳态基本无振幅;PID控制从0 m深度位置开始经过约6 s进入稳定状态,有峰值和超调,稳态具有一定振幅.再给定ROV定深至6 m位置,加入一个模拟浪涌约10 N的垂直方向的定深扰动,滑模控制中模拟量从0 m深度开始经过约4 s进入稳定状态,并且无超调,稳态基本无振幅;PID控制从0 m深度位置开始经过约9 s进入稳定状态,有峰值和超调,稳态具有一定振幅.

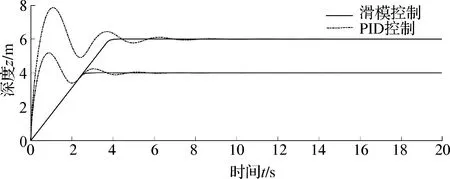
图9 ROV定深仿真变化图

4 结语

本文介绍了基于滑模控制的ROV控制器,搭建了ROV的数学模型,设计了整体控制系统,对ROV的偏航角和深度控制进行Simulink仿真,对ROV进行动力学分析,进而推导出静止坐标系和运动坐标系之间的坐标变换.根据建立的ROV运动学和动力学模型,应用Matlab/Simulink仿真软件对ROV进行系统仿真,得到的仿真结果验证了ROV滑模控制系统的有效性和稳定性.