塞罕坝华北落叶松人工林树冠外部轮廓模型*
2021-07-16赵婷婷王冬至张冬燕黄选瑞
赵婷婷 王冬至,2 张冬燕,3 郭 立 黄选瑞,2
(1.河北农业大学林学院 保定 071000; 2.河北省林木种质资源创新与保护实验室 保定 071000; 3.河北农业大学经济管理学院 保定 071000; 4.丰宁千松坝林场 承德 068350)
树冠是树木进行光合作用、呼吸作用和蒸腾作用等一系列生理活动与环境进行物质交换和能量转化的主要部位(李凤日, 2004; 郭孝玉, 2013),其形状和大小在生物多样性、林木竞争(Crecente-Campoetal., 2009; Sadono, 2015)、光拦截(Stercketal., 2001)、碳估计(Gaoetal., 2017)、生产力及经营效果评价(Tanabeetal., 2001)等研究领域具有重要作用。树冠外部轮廓是将每轮最大枝条的梢头连接所构成的曲线,其不仅是树冠形状和大小的直观表现(刘兆刚等, 1996; Hemeryetal., 2005),而且是研究树冠表面积、树冠体积的基础以及模拟林分动态生长的依据(Jahnkeetal., 1965)。因此,构建树冠外部轮廓预测模型,对了解树木生长发育的动态变化规律有重要意义。
目前,国内外关于树冠外部轮廓模型的研究已由简单几何形状、分段函数等发展为比较灵活的可变指数方程,以幂函数(吴明钦, 2014)、修正Kozak方程(高慧淋, 2017; 高慧淋等, 2018)和修正Weibull方程(Ferrareseetal., 2015; Sunetal., 2017)等为主,多采用最小二乘法估计模型参数。最小二乘法要求模型残差项满足正态分布、方差齐性且独立特性,由于枝条数据多具有时间相关性和空间异质性,因此需要发展新的方法来弥补这种不足。李春明(2009)、符利勇等(2012)研究表明,混合效应模型能够有效解决以上问题,如部分学者基于非线性混合效应模型构建地位指数模型(Zangetal., 2016; Özçeliketal., 2018; 符利勇等, 2011)、冠幅预测模型(Fuetal., 2017; Dongetal., 2016a; 2016b)、直径生长模型(Bohoraetal., 2014)、心材预测模型(贾炜玮等, 2018)等,结果均表明非线性混合效应模型预测精度更高。为了描述树冠最大外部轮廓,Sun等(2017)基于分位数回归模型构建了樟子松(Pinussylvestrisvar.mongolica)树冠外部轮廓模型。分位数回归可通过特定分位数构建多个分位数回归方程,寻找因变量和自变量之间的关系,当因变量不同于条件均值时,分位数回归优势显著(Weiskitteletal., 2011),已在自疏边界线模型(Zhangetal., 2005)、直径分布模型(Mehtätaloetal., 2008)、林分密度指数(Duceyetal., 2010)、直径生长模型(Bohoraetal., 2014)构建等方面得到了大量应用。
在树木生长过程中,冠形会受胸径(diameter at breast height,DBH)、树高(height of the tree,HT)、冠长(crown length,CL)、冠幅(crown width,CW)、冠高比(crown height ratio,CHR)、高径比(height to diameter ratio,HDR)、林分年龄(stand age,Age)、林分密度(stand density,Sd)等多种树木和林分因子影响(郭艳荣等, 2015; 高慧淋等, 2017; Doruskaetal., 1998),基于非线性混合效应模型和分位数回归模型构建包含树木和林分因子的树冠外部轮廓预测模型是一个亟待解决的科学问题。本研究以河北省塞罕坝机械林场华北落叶松(Larixprincipis-rupprechtii)人工林为研究对象,利用幂函数、修正Kozak方程和修正Weibull方程选取适用于描述树冠外部轮廓的最优模型,通过相关分析确定影响树冠外部轮廓的主要因子,采用非线性混合效应模型和非线性分位数回归模型构建树冠外部轮廓预测模型,并比较分析2种模型的预测精度,以期为准确预测树冠生长发育规律及预估生产力提供科学依据。
1 研究区概况与数据来源
1.1 研究区概况
研究区位于河北省承德市塞罕坝机械林场(41°22′—42°58′N,116°53′—118°31′E),为阴山山脉与大兴安岭余脉的交界地带,地势北高南低,海拔1 010~1 940 m。属华北暖温带气候类型区,年均气温-1.2 ℃,年均最高气温33.4 ℃,年均最低气温-43.3 ℃,年均降水量约452.2 mm,主要集中在6—8月,年日照时数2 548.7 h。土壤类型以褐色森林土、棕色森林土、砂壤土、壤土、风沙土、沼泽土、砾石土、草甸土为主,成土母质主要为坡积物、残积物、冲积物、沉积物和风积物。主要乔木树种有华北落叶松、白桦(Betulaplatyphylla)、云杉(Piceaasperata)、樟子松、山杨(Populusdavidiana)、油松(Pinustabulaeformis)、蒙古栎(Quercusmongolica)等。
1.2 数据来源
2018年7—8月,在塞罕坝机械林场设置10块华北落叶松人工林标准地(0.06 hm2),调查林分年龄(Age,a)、林分密度(Sd,tree·hm-2)、平均胸径(mean DBH,cm)、平均树高(mean HT,m)、平均冠幅(mean CW,m)和平均冠长(mean CL,m),统计结果见表1。按照等断面积径级标准木法将标准地内所有树木分为3个等级,每个等级选择2株标准木进行树干解析(样地9、10分为5个等级,每个等级选择1株标准木),解析木伐倒前测量其胸径(DBH)和冠幅(CW),伐倒后测量其树高(HT),并将第一活枝高处定为冠基高度(height at the base of the crown,HBC,m)、冠长(CL)定为CL= HT- HBC、冠长率(crown length rate,CLR)定为CL与HT的比值,高径比(HDR)定为HT与DBH的比值。树冠按1 m为1个区分段进行枝解析,观测枝条基径(branch diameter,BD,mm)、枝条长度(branch length,BL,cm)、弦长度(branch chord length,BC,cm)、着枝角度(branch angle,BA,°)和着枝深度(depth into crown,DINC,m)等变量,共调查解析木58株和1 789个枝条数据。根据枝条各属性通过三角函数关系计算梢头处树冠半径(crown radius,CR,m)和相对着枝深度(relative DINC,RDINC,m),CR=BC·sinBA,RDINC=(DINC- BC·cosBA)/CL。对所有解析木,每轮选取1个最大枝条(半径最大)作为构建树冠外部轮廓的样本,共672个最大枝条。每块标准地随机选取1株解析木作为检验样本,其余解析木作为建模样本,建模样本与检验样本样木及枝条属性因子统计如表2所示。

表1 华北落叶松人工林林分因子统计Tab.1 Statistics for stand variables of L. principis-rupprechtii plantation
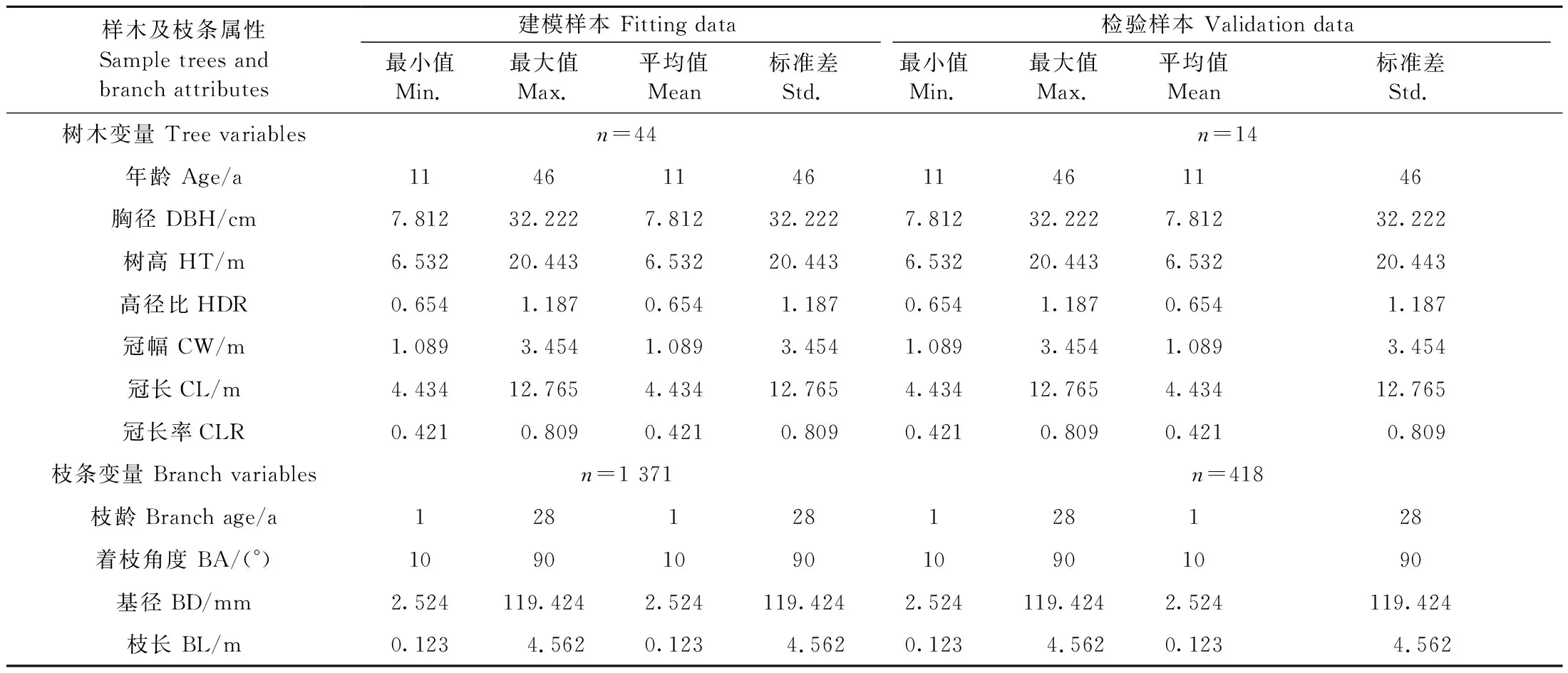
表2 华北落叶松人工林解析木及最大枝条变量统计Tab.2 Statistics for attributes of sample trees and branch of L. principis-rupprechtii plantation
2 研究方法
2.1 基础模型选择
吴明钦(2014)利用可变幂函数方程拟合了杉木(Cunninghamialanceolata)树冠外部轮廓; Ferrarese等(2015)利用修正Weibull方程拟合了美国黄松(Pinusponderosa)树冠外部轮廓; Sun等(2017)通过对比幂函数方程、修正Kozak方程和简单多项式方程对蒙古栎树冠外部轮廓进行了拟合。在描述树冠外部轮廓的众多模型中,幂函数、修正Kozak方程和修正Weibull方程(表3)是最常用的模型,因此本研究以幂函数、修正Kozak方程和修正Weibull方程作为构建塞罕坝华北落叶松人工林树冠外部轮廓的基础模型。

表3 基础模型选择Tab.3 The basic model selection
2.2 两水平非线性混合效应模型
非线性混合效应模型是基于回归函数依赖于固定效应和随机效应的非线性关系而建立的回归模型(符利勇等, 2015)。本研究考虑样地和嵌套在样地中样木对树冠半径的影响,将样地和嵌套在样地中样木作为随机效应因子,构建嵌套两水平非线性混合效应模型,形式如下:
(1)
式中:M为样地数;Mi为第i块样地中嵌套样木株数;nij为第i块样地中第j株样木所测量树冠半径个数;yijk和vijk分别为第i块样地中第j株样木第k次重复调查时因变量和自变量的观测值;f(·)为树冠外部轮廓基础模型;β为p×1维固定效应参数;ui为q1×1维的第i块样地产生的随机效应,假定服从期望为 0、方差-协方差矩阵为ψ1的正态分布;uij为q2×1维的第i块样地中第j株样木产生的随机效应,假定服从期望为0、方差-协方差矩阵为ψ2的正态分布;φijk为形式参数(简称形参),与β、ui和uij呈线性函数关系;Aijk、Bi,jk和Bijk分别为β、ui和uij的设计矩阵;εijk为随机误差项,假定服从期望为 0、方差为R的正态分布,并假定ui、uij和εijk误差项之间相互独立。
将所有参数及其组合作为随机效应进行拟合,通过比较赤池信息准则(Akaike information criterion,AIC)、贝叶斯信息准则(Bayesian information criterion,BIC)和最大似然估计(maximum likelihood estimation,logLik),确定最优随机效应组合构造类型。对选取不同个数参数效应的最优模型进行似然比检验,以约束模型中参数个数。样地(样木)内方差-协方差结构Ri如下:
(2)
式中:σ2为模型的残差方差; Гi为样地(样木)内误差相关性结构;Gi为描述方差异质性的对角矩阵。
采用幂函数(3)和指数函数(4)校正模型,以消除数据间的异方差性:
Var(eij)=σ2exp(2δvij);
(3)
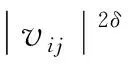
(4)
分别用复合对称(complex symmetry)、对角矩阵(diagonal matrix)和广义正定矩阵(general positive-definite matrix)表示样地(样木)内误差相关性结构。
2.3 非线性分位数回归模型
分位数回归是Koenker等(1978)提出的,主要用于分析综合响应变量(y)在各分位点与解释变量(x)的关系。与最小二乘法相比,分位数回归具有单调同变性及对异常值不敏感性,且在存在显著异方差的情况下具有较强稳健性(Cadeetal., 2003)。设随机变量(x,y),y的分布函数如下:
F(y)=P(Y (5) 对于任意分位数0 (6) 式中:F-1(q)为x的q分位点。 非线性混合效应模型如下: CRijk=f(X,θ)+εijk。 (7) 式中: CRijk为第i株样木第j轮第k个枝条的半径观测值;f(X,θ)代表基础模型形式;εijk为模型误差项。 q选取不同分位点,代表不同分位点的估计值,通过反映不同分位点的数据趋势,拟合参数估计结果。 任意分位点处各参数的估计值通过下式计算: (8) (9) 式中:NT、Ni、Nij分别代表样木总株数、第i株样木总轮数和第i株样木第j轮枝条总数; 式(9)为损失函数。 Parente等(2016)研究证明,在线性回归分位数中当误差项存在组内相关但组间独立时,分位数回归估计值是一致并渐近正态的,渐近结果也可推广到非线性分位数回归,这为利用式(8)分位数估计值构建树冠外部轮廓非线性分位数回归模型提供了必要的理论基础和经验支持。Koenker等(1996)提出求解非线性分位数回归模型的“内点法”,该方法于R语言quantreg软件包中的nlrq函数得以实现(Koenker, 2019)。 采用赤池信息准则(AIC)、贝叶斯信息准则(BIC)、最大似然估计(logLik)、确定系数(R2)、均方根误差(root mean square error,RMSE)、平均相对误差(mean relative error,MRE)对模型拟合与检验结果进行评价。计算公式如下: AIC=-2LL+2p; (10) BIC=-2lnL+klnn= NlnSSE-nlnn+lnnp; (11) (12) (13) (14) 式中:p为模型参数个数; LL为最大似然函数的对数值; ln(n)为n的自然对数。 基于最小二乘法分别对幂函数、修正Kozak方程和修正Weibull方程进行拟合与评价(表4),结果发现幂函数均方根误差(RMSE)、平均相对误差(MRE)最小,确定系数(R2)较大,因此本研究选择幂函数作为构建华北落叶松人工林树冠外部轮廓的基础模型。 设树冠外部轮廓梢头处树冠半径为0,且树冠外部轮廓存在唯一拐点,MCR(maximum CR)和MRDINC(maximum RDINC)分别代表树冠外部轮廓拐点处最大树冠半径和最大相对着枝深度位置。对MCR、MRDINC进行Pearson相关性分析(表5),结果发现MCR和MRDINC受林分年龄(Age)、冠长(CL)、胸径(DBH)、树高(HT)、冠高比(CHR)和高径比(HDR)影响较大,其中MCR与Age、CL、DBH、HT、CHR呈正相关、与HDR呈负相关,MRDINC与Age、CL、DBH、HT、CHR、HDR均呈负相关。 表5 树冠变量与影响因子的相关系数Tab.5 Correlation coefficient of crown variables with impacting factors respectively 基于描述树冠外部轮廓的基础模型及其主要影响因子,构建包含主要影响因子的非线性混合效应模型如下: (15) 混合效应模型拟合结果见表6,同时考虑样木和样地随机效应的两水平混合效应模型(15.3)比只考虑样木效应的模型拟合效果好。在两水平混合效应模型中,模型(15.3)AIC、BIC最小,且通过LRT检验,为参数较少的最优混合效应模型。 表6 不同随机效应组合混合模型拟合结果Tab.6 Fitting results of different random effects combined models 为了减小模型方差异质性,分别采用指数函数、广义幂函数和幂函数消除模型异方差,不同方差函数混合效应模型拟合结果比较(表7)发现,加入方差函数的模型AIC明显下降,表明样地(样木)效应并未完全消除数据间的异方差性,3种方差函数中幂函数表现良好,广义幂函数与幂函数差异并不明显,因此本研究选择幂函数作为方差函数。模型估计结果如表8所示。 表7 不同方差函数混合效应模型拟合结果比较Tab.7 Fitting results comparison based on different variance functions 表8 混合效应模型拟合结果Tab.8 Mixed effects model fitting results 基于最大枝条数据对各分位点的非线性分位数回归模型参数进行拟合(表9),随着分位数增加,参数a1逐渐减小,a3先增大后减小再增大,a2、a5、a6逐渐增大,且所有参数估计值符号未发生改变,参数估计的稳定性较强。利用0.50、0.55、0.60、0.65、0.70、0.75、0.80、0.85、0.90和0.95不同分位数模型模拟不同龄组树冠外部轮廓(图1),不同分位数树冠外部轮廓曲线在0.50~0.95范围内有较强的规律性,随着分位数增大,树冠外部轮廓曲线逐渐由树冠中心位置向树冠外侧边缘移动。除q=0.95分位数树冠外部轮廓曲线明显偏离树冠外部轮廓边界点外,0.50~0.90分位数树冠外部轮廓曲线描述树冠外部轮廓比较稳定,总体趋势一致。R2在分位数0.65~0.75时达到最大值,表明该范围内分位数回归模型能够较好描述最大树冠外部轮廓的平均变化趋势,但并不能很好表示树冠最大外部轮廓。在分位数0.50~0.90范围内,随着q增加,分位数模型曲线无限接近树冠最大外部轮廓,相对于其他分位数,0.90分位数回归模型最接近树冠最大外部轮廓。 表9 分位数回归模型拟合结果Tab.9 Quantile regression model fitting results 图1 不同龄组华北落叶松人工林树冠外部轮廓的分位数回归曲线Fig. 1 The predicted crown profile for different age groups of L. principis-rupprechtii plantation by quantile models 基于混合效应模型和分位数分别为0.80、0.85、0.90、0.95的分位数回归模型,利用检验数据对不同龄组华北落叶松人工林进行模拟。对比不同分位数回归模型与混合效应模型拟合结果(图2),混合效应模型树冠外部轮廓曲线小于分位数回归模型,且随着q增加,分位数回归模型树冠外部轮廓曲线由树冠中心位置逐渐向树冠外侧边缘移动。q=0.95时,曲线偏离树冠外部轮廓外侧,q=0.90时,曲线最接近树冠外部轮廓。当树冠相对着枝深度小于0.7时,混合效应模型曲线与q=0.90时分位数回归模型曲线均可较好描述树冠外部轮廓,当树冠相对着枝深度大于0.7时,混合效应模型曲线能够更准确描述冠基处的平均外部轮廓,分位数回归模型能更好显示树冠最大外部轮廓。 利用检验数据对混合效应模型和q=0.90分位数回归模型在不同着枝深度处的残差进行比较(图3),混合效应模型和分位数回归模型的残差均接近0,混合效应模型有效描述了树冠最大枝条的平均曲线,分位数回归模型则准确确定了树冠最大外部轮廓。 树冠外部轮廓描述树冠最外层树冠边缘的特征,与树冠形状和大小相关,是树冠研究的重要内容 (Crecente-Campoetal., 2013; Stercketal., 2001)。高慧淋等(2018)以分段抛物线方程、修正Kozak和Weibull方程为基础模型构建黑龙江省红松(Pinuskoraiensis)和长白落叶松(Larixolgensis)树冠外部轮廓模型,高慧淋等(2019)基于Kozak方程构建樟子松树冠外部轮廓模型,树种特征是决定树冠形状的主要因素,最适合描述其他树种的模型可能并不适合描述华北落叶松人工林树冠外部轮廓,因此,本研究从常见描述树冠外部轮廓的模型中确定一个拟合效果较好的模型作为基础模型,结果发现幂函数拟合华北落叶松人工林树冠外部轮廓优于修正Kozak方程和修正Weibull方程。Crecente-Campo等(2009)构建树冠外部轮廓模型包含DBH、CL、HT等树木因子,Baldwin等(1997)构建包含DBH、HT、CHR等树木因子的二次多项式模型拟合火炬松(Pinustaeda)树冠形状,发现树冠外部轮廓受不同树木因子影响。Wang等(2016)提出除树木因子外还应考虑林分因子对树冠外部轮廓模型的影响,郭艳荣等(2015)基于不同龄组样木数据构建树冠外部轮廓模型,结果表明林分年龄对树冠形状有一定影响。因此,本研究通过对不同林分因子和树木因子进行相关分析,将林分因子中的林分年龄(Age)以及树木因子中的冠长(CL)、胸径(DBH)、树高(HT)、冠高比(CHR)和高径比(HDR)加入模型中,提高了华北落叶松人工林树冠外部轮廓模型拟合精度。 非线性混合效应模型能够有效处理符合层次结构特点的数据,对提高模型精度具有显著效应(李春明等, 2010; 符利勇等, 2012)。高慧淋等(2017)考虑单水平(样地)效应构建树冠外部轮廓混合效应模型,以DBH、CL、HDR对应参数作为随机效应参数充分解释了样地内的变化。高慧淋等(2019)通过对比单水平(样地或样木)混合效应模型与两水平混合效应模型,发现DBH对应参数同时考虑样地和样木效应,HDR、RDINC对应参数考虑样木效应的两水平混合效应模型优于单水平(样地或样木)混合效应模型。本研究所用数据符合样地-样木-枝条层次结构,混合效应模型是处理该问题强有力的方法,对比样木效应混合模型与样地-树木两水平混合效应模型,两水平混合效应模型可明显改善模型拟合精度,当HDR对应参数考虑样地效应,CHR、RDINC对应参数考虑样木效应时,模型拟合效果最好。 分位数回归不仅能够描述树冠外部轮廓的平均变化趋势,而且还能得到任意分位点的树冠外部轮廓 (Zangetal., 2016; Özçeliketal., 2018),Sun等(2017)基于不同分位点建立樟子松树冠轮廓模型,通过对比平均误差和绝对误差,确定q=0.95时分位数回归曲线较接近树冠轮廓。与Sun等(2017)研究方法一致,本研究利用0.50~0.95间隔为0.05作为分位点拟合华北落叶松人工林树冠外部轮廓,除q=0.95分位数树冠外部轮廓曲线明显偏离树冠外部轮廓边界点外,0.50~0.90分位数树冠外部轮廓曲线描述树冠外部轮廓比较稳定,且分位点为0.90时模型更适合描述华北落叶松人工林树冠外部轮廓。精准预测树冠外部轮廓是进一步研究树冠表面积和体积的必要前提(Cadorietal., 2016; 吴丹子等, 2020),但树冠外部轮廓会受到经营措施和空间竞争等因素影响(Wangetal., 2016; Garberetal., 2005),因此如何解决不同经营措施和空间竞争等因素对树冠外部轮廓特征产生的影响还需进一步深入研究。 构建华北落叶松人工林树冠外部轮廓模型时,幂函数为描述树冠外部轮廓的最优基础模型,林分年龄、冠长、胸径、树高、冠高比、高径比是影响树冠外部轮廓的主要因子。同时考虑样地和样木效应的两水平混合效应模型优于样木效应的单水平混合效应模型,可明显提高模型拟合精度,精确描述树冠外部轮廓的平均趋势。除研究条件均值外,分位数回归模型可灵活表示不同分位点树冠外部轮廓,对树冠外部轮廓边界研究具有重要意义。2.4 模型评价与检验
3 结果与分析
3.1 基础模型确定
3.2 影响树冠外部轮廓的主要因子

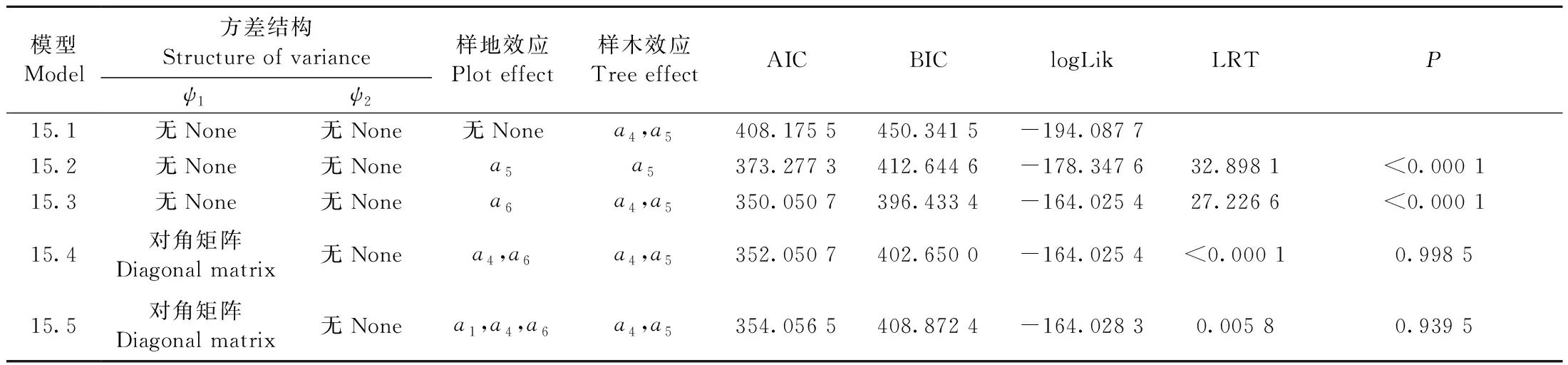
3.3 两水平非线性混合效应模型构建


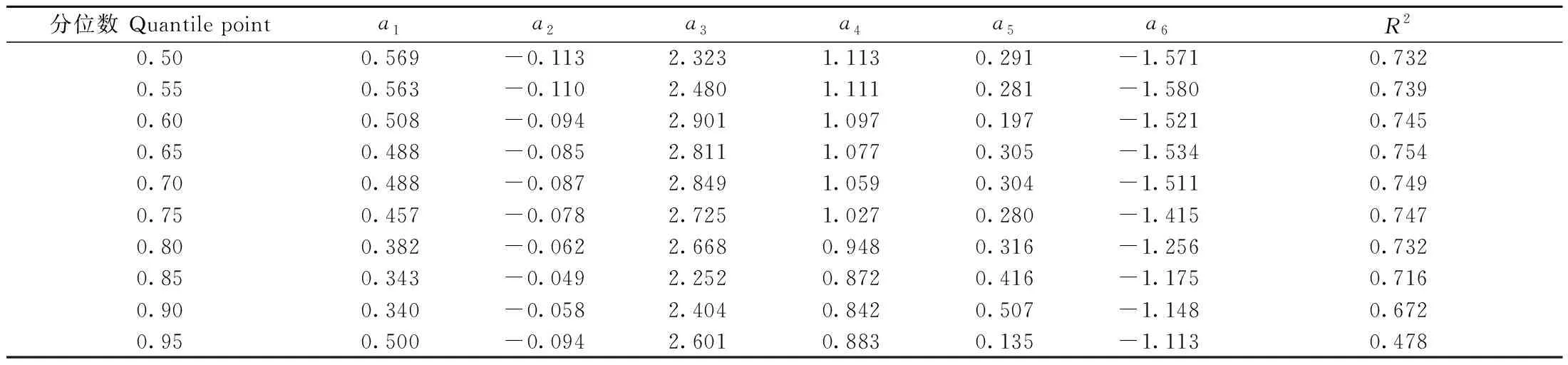
3.4 非线性分位数回归模型构建
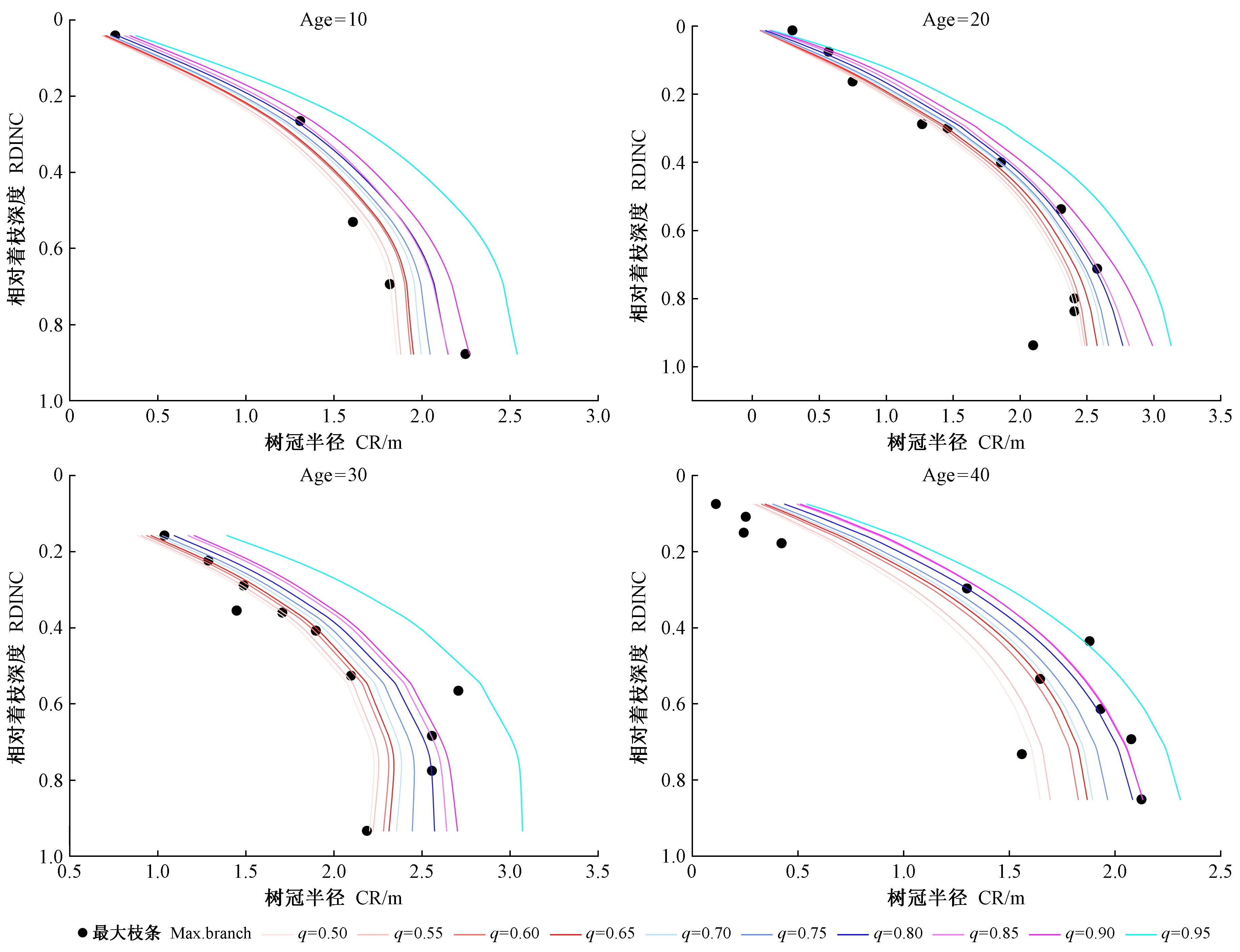
3.5 树冠外部轮廓模拟
3.6 模型评价与检验
4 讨论
5 结论
