含多间隙弹性约束机械振动系统的动力学特性

尹凤伟，马 琳，马娟娟

(兰州交通大学 机电工程学院，兰州 730070)

机械结构与系统的非线性振动是工程实际中的复杂问题.由于在几何关系、约束条件、拓扑结构、激励因素、耦合方式等方面存在非线性因素，因此深入研究非线性振动以便更精准地描述机械系统的动力学特征.掌握非线性振动的产生与传播机理，对于设计制造安全和性能优良的机械系统至关重要.国内外学者通过定性分析、数值计算和实验等方法研究了含间隙、约束振动系统的周期运动及分岔特征、擦碰奇异性和颤冲击-粘滞振动系统.Nordmark[1]研究了带有刚性限幅约束的单自由度周期受迫振子的运动特性.Luo等研究了带有单侧刚性约束[2]和对称刚性约束副[3]的周期受迫振动系统的低频振动特性，发现转迁域结点为其中一个基本周期冲击振动的二重Grazing余维二分岔.朱喜锋[4]研究了含间隙机械振动系统的动力学特性与参数匹配规律.乐源[5]研究了一类三自由度碰撞振动系统的激变和阵发性，分析了拟周期-拟周期阵发性动力学现象.张惠和丁旺才等[6]针对一类单自由度含间隙和预紧弹簧的弹性碰撞振动系统的分岔控制问题，提出了一种基于Lyapunov指数及径向基函数神经网络的分岔预测及控制方法.叶建聪和石慧荣等[7]揭示了间隙和干摩擦对振动系统的周期运动和分岔特性的影响.李得洋和丁旺才等[8]采用线性反馈控制方法研究了一类两自由度含弹性约束碰撞振动系统共存吸引子转迁控制问题.Wagg[9-10]研究了一类带有多刚性约束的两自由度振动系统的低频振动特性，分析了其低频域内的颤碰-粘滞振动及Rising现象.颉成利和石慧荣等[11]计算了含预压约束的两自由度受迫振动系统的动力学特性，分析了预压量与颤-冲击振动的关系.Yin[12]针对含多间隙-非对称刚性约束的两自由度受迫振动系统，分析和计算了机械振动系统质块冲击刚性约束时引发完整颤-冲击振动的判断条件和动力学特性.吕小红[13]研究了一类碰撞-渐进振动系统的粘滞振动及分岔特性.赵国庆[14]计算了两级齿轮传动系统的非线性动力学特征.覃泽锋等[15]研究了考虑油膜力-碰摩故障的双盘转子系统非线性动力学行为.王红兵和李国芳等[16]通过仿真计算，分析了高速车辆车轮踏面磨耗预测及系统参数影响.Liu和Pavlovskaia等[17]提出了由置于基架的弹性限幅板、线性DC伺服电动机和简谐激励的金属棒构成的舱型振动冲击模型；通过改变支承弹簧的刚度和激振频率，对舱体的动力学进行了实验研究.

本文在Wagg研究的基础上，基于多参数耦合、多目标协同仿真分析，研究含多间隙-弹性约束两自由度受迫振动系统的非线性动力学特性.而Wagg研究的带有刚性约束的振动系统可视为带有弹性约束振动系统的一种典型状态.

1 系统的力学模型

图1为一类两自由度含多间隙弹性约束振动系统的力学模型.质块M1与质块M2通过刚度为K1的线性弹簧和阻尼系数为C1的线性阻尼器联接，质块M2经刚度为K2的线性弹簧和阻尼系数为C2的线性阻尼器连接于支承基础.简谐激励力Pisin(ΩT+τ)作用于质块Mi(i=1,2)，其中Pi、Ω和τ表示系统的简谐力振幅、频率和初相位.质块M1右侧和质块M2左、右侧均置有刚度系数K0的弹性约束，约束刚度取值范围为K0∈(0,∞).当简谐力较小时，系统呈现无冲击受迫振动.随简谐力增大，当质块M1的位移满足X1=B1时，或质块M2的位移满足|X2|=B2时，质块M1或质块M2与其对应的弹性约束处发生软冲击[18].

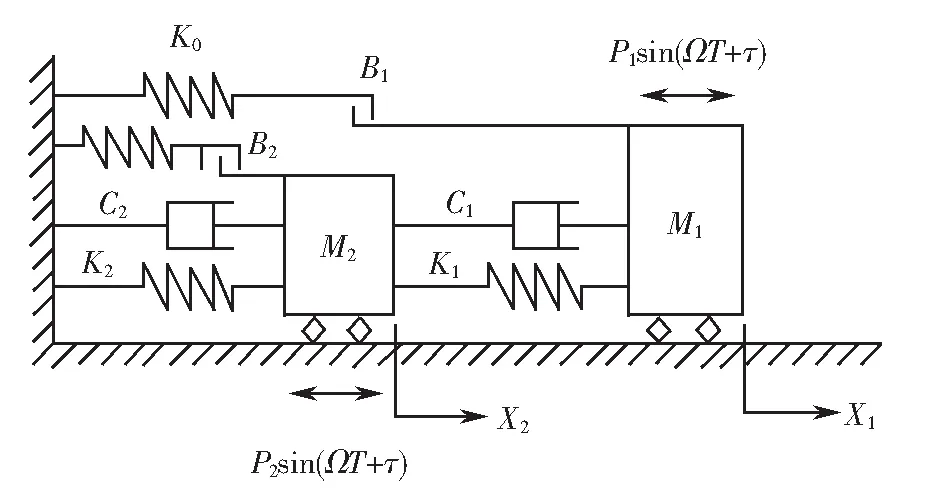
图1 力学模型Fig.1 Mechanical model

引入无量纲量参数、变量和时间：

(1)

系统的无量纲运动微分方程：

(2)

其中，

(3)

(4)

根据无量纲化的系统参数(1)，可确定系统部分参数的取值范围：μm∈(0,1)，μk∈(0,1)，μc∈(0,1)，μk0∈(0,1)，f∈[0,1].

2 系统的Poincaré映射

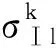
(5)

X(i+1)=f(X(i),ν),

(6)

(7)

(8)

上式(6),(7)和(8)中，X∈R4,ν是系统参数，ν∈R8.

3 数值分析

对图1振动系统，在其参数定义域内取一组无量纲参数作为基准参数：μm=0.5,μk=0.5,μc=0.5,f=0.5,μk0=0.95.在同一范畴下，基于多参数耦合、多目标协同仿真分析，揭示了振动系统间隙阈值(δ)和激励频率(ω)等关键参数与系统周期振动的映射关系.数值计算结果(如图2a)表明了系统在(ω,δ)-参数平面内的周期冲击振动模式类型、分布规律和分岔特征.本文中(ω,δ)-参数平面图中未标注的60%黑色区域表示未辨识的长周期振动或混沌.同时也未进一步对概周期振动和混沌进行辨识区分，本文暂均称为混沌.数值计算结果表明当间隙阈值较大时(δ>1.5)，系统在高频域内主要表现为0/1无冲击自由振动；在低频域内表现为0/1、1/1基本周期振动和少量的1/2、2/2周期冲击振动.当间隙阈值较小时(δ≤1.5)，质块M1在高频域内表现为1/2、2/2、3/3、4/3、2/4、3/4、4/4等亚谐周期振动；在低频域内，质块M1主要表现为1/1、2/1、3/1、4/1、5/1…q/1(q≥6)等基本周期冲击振动和少量的3/2、4/2…q/2(q≥6)等亚谐周期振动，如图2(a)所示.

如图2(b)所示，当间隙阈值较大时(δ>1.0)，质块M2在高频域内主要表现为1-0-0无冲击受迫振动；在低频域内表现为1-0-1、1-1-1、1-2-1、1-2-0、1-1-0等基本周期振动和少量的2-0-0、2-3-2等亚谐周期振动.当间隙阈值较小时(δ≤1.0)，质块在高频域内表现为4-2-0、2-1-0、2-1-1、2-2-1、2-2-2、4-4-4、4-4-3等亚谐周期振动；在低频域内，质块M2主要表现为1-3-0、1-3-1、1-3-2、1-4-0、1-4-1、1-4-2、1-5-0、1-5-1…1-p-q(p≥6或q≥6)等非对称的各类基本周期冲击振动和少量的2-3-2、2-5-2…2-p-q(p≥6或q≥6)等亚谐周期振动.

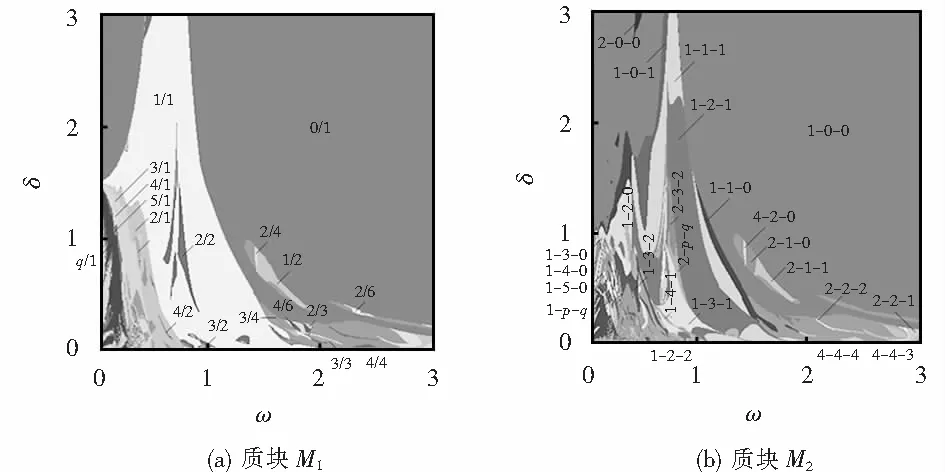
图2 系统周期振动在(ω,δ)-参数平面上模式类型Fig.2 Mode types of periodic vibration of system on (ω,δ)-parameter plane

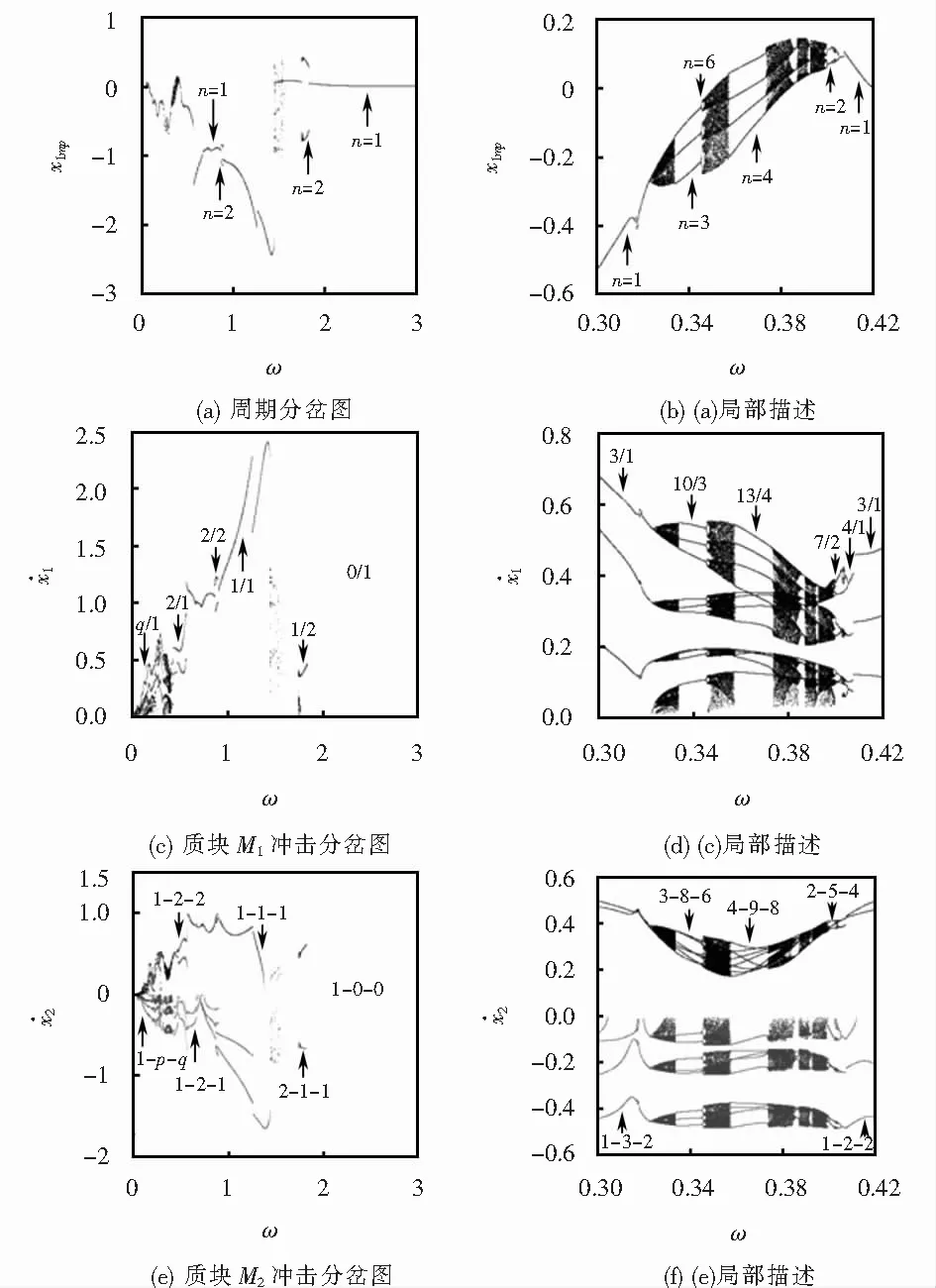
图3 δ=0.43,系统分岔图Fig.3 Bifurcation diagram of the system,δ=0.43

结合图2(a)，图3(a)和(b)，图4代表性的揭示了质块M1由5/1周期振动经Real-grazing分岔转迁入稳定的6/1周期振动.图4(a)取间隙阈值δ=0.43且激励频率ω=0.233 3时，质块M1表现为5/1周期冲击振动(图4(b)是图4(a)的局部描述)，随ω减小到ω=0.233 22时发生5/1周期振动擦切接触(图4(d)是图4(c)的局部描述)，当激励频率ω=0.233 20时质块M1显示为6/1周期振动(图4(f)是图4(e)的局部描述).在ω∈[0.332,0.333]区间内，随激励频率ω的减小质块M1经历一次Real-grazing分岔转迁；反之随激励频率(ω)增大，质块M1则由6/1周期振动经鞍结分岔转迁为5/1周期振动.

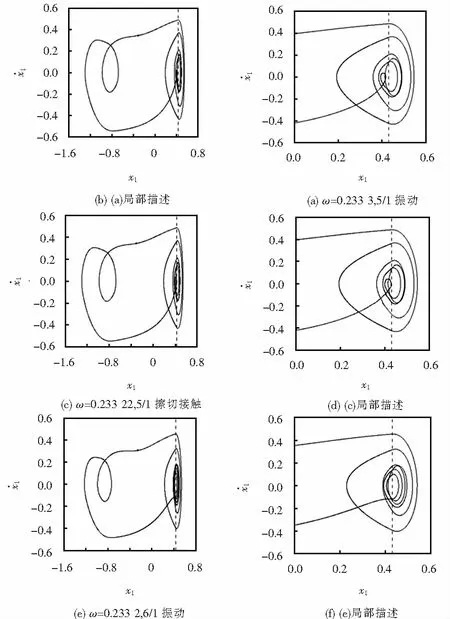
图4 δ=0.43,质块M1相图 Fig.4 Phase diagram of mass M1,δ=0.43

同样的Real-grazing分岔特性在质块M2上也可观察到.如图5所示，取间隙阈值δ=0.43，当激励频率ω=0.413时，质块M2显示为1-2-2周期冲击振动(图5(b)是图5(a)的局部描述)，随ω减小到ω=0.411 2时发生1-2-2周期振动擦切接触(图5(d)是图5(c)的局部描述).随即当激励频率ω=0.410时，质块M2表现为1-3-2周期振动(图5(f)是图5(e)的局部描述).在ω∈[0.410,0.413]区间内，随激励频率(ω)的减小质块M2经历一次Real-grazing分岔转迁；反之随激励频率(ω)增大，质块M2则由1-3-2周期振动经鞍结分岔转迁为1-2-2周期振动.

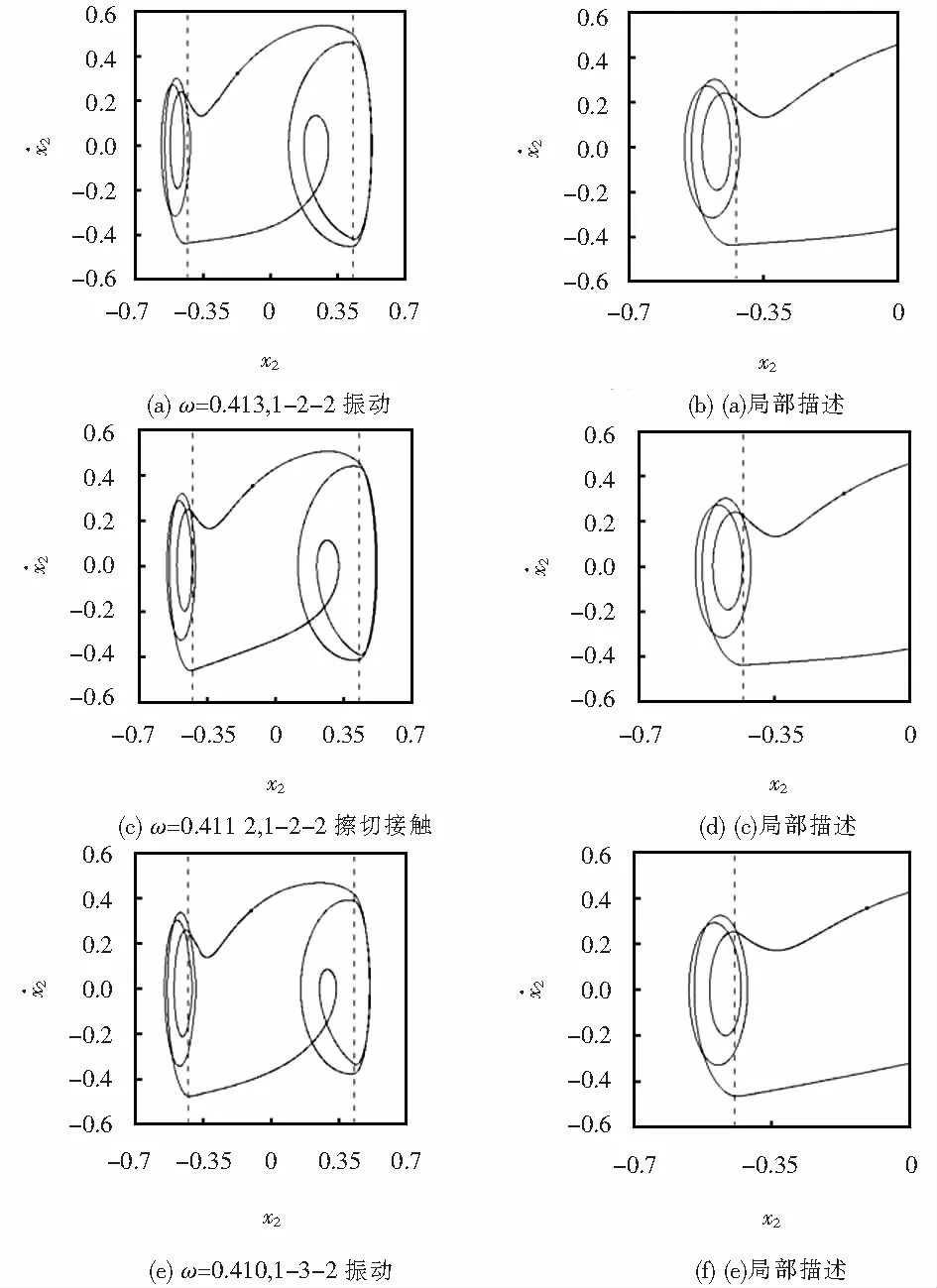
图5 质块M2相图，δ=0.43Fig.5 Phase diagram of mass M2,δ=0.43

图6是对振动系统在基准参数下计算结果的进一步数值仿真计算，且取间隙阈值δ=0.1.在同一范畴下与图3进行对比，计算结果显示随间隙阈值(δ)的减小，系统表现出更为复杂的动态特性.图6(a)表明系统在低频区主要表现为1周期振动，在高频区表现为2周期振动，然而在1周期振动演化为2周期振动过程中，系统显示出复杂的动力学特性，见图6(b).取激励频率ω∈[1.7,2.95]区间时，随ω增大，质块M1的1/1周期振动嵌入混沌后退化为3/3亚谐周期振动和2/3亚谐周期振动.随ω继续增大，质块M1表现为2/2、4/4、3/6等亚谐振动.随后质块M1由混沌经逆周期倍化分岔演化为1/2亚谐周期振动，见图6(d).在相同的激励频率取值ω∈[1.7,2.95]区间内，随ω递减，质块M2由2-2-1周期振动演化为1-1-0周期振动过程中，出现了2-2-2、4-4-4、4-4-3、8-8-7、6-6-4、2-2-1、3-4-1、3-3-2等亚谐周期振动，见图6(f).

结合计算结果图2、图3和图6，当间隙阈值(δ)取值越小，系统的非光滑特征越显著，导致低频域内基本周期冲击振动群的量增大，即q/1(或1-p-q)周期振动显著增多，且相邻基本周期冲击振动经Bare-grazing分岔转迁过程中的亚谐周期振动模式类型表现出复杂性和多样性特征.由于系统带有多重间隙弹性约束，使系统M2在低频域内出现了大量的非对称基本周期冲击振动群.随激励频率ω进一步减小，当系统各质块的冲击次数(p或q)变得足够大时，系统的基本周期冲击振动表现为颤-冲击振动特性.取间隙阈值δ=0.1，当激励频率ω=0.18时，系统质块M1表现为10/1周期振动，质块M2表现为1-9-2周期振动(见图7).然而在相同参数条件下，当激励频率减小为ω=0.1时，系统质块M1于其右侧弹性约束处的冲击次数q显著增多，并表现为颤-冲击振动特征；质块M2则于其右侧弹性约束处的冲击次数明显增大，也表现出颤冲击振动特征(见图8).

图6 系统分岔图,δ=0.10Fig.6 Bifurcation diagram of the system,δ=0.10

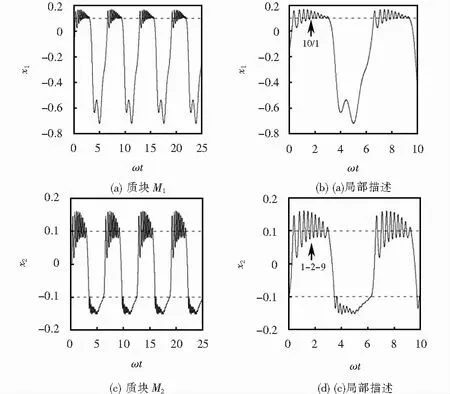
图7 δ=0.1,ω=0.18,时间历程图Fig.7 Time response figure,δ=0.1,ω=0.18

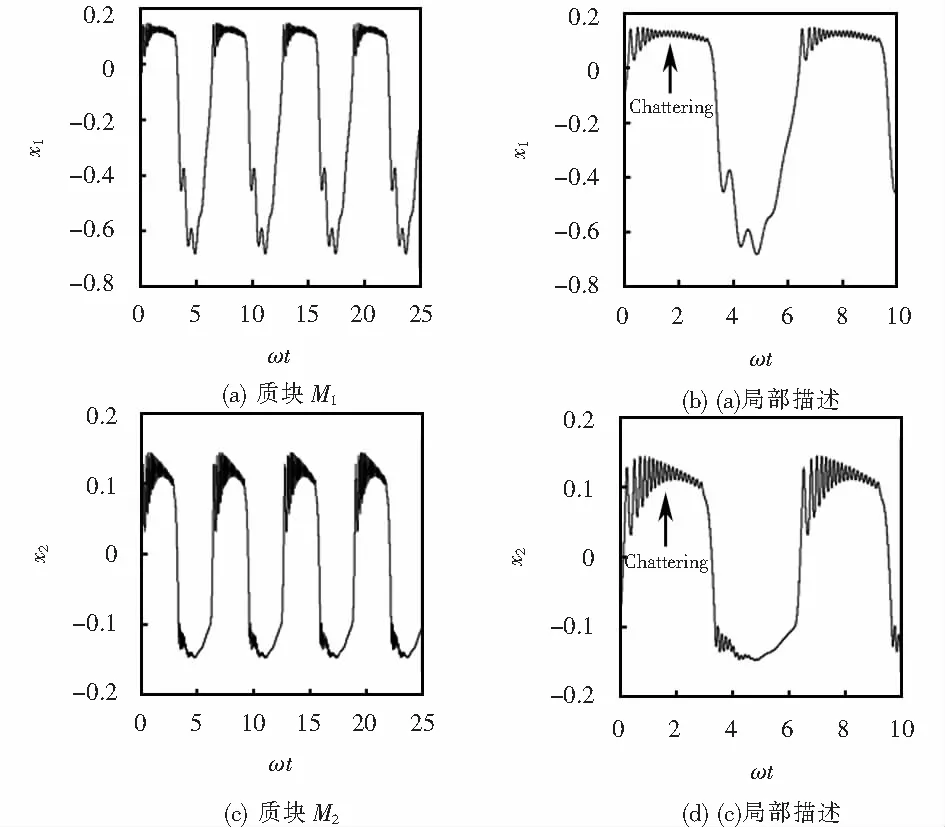
图8 δ=0.1,ω=0.1,时间历程图Fig.8 Time response figure,δ=0.1,ω=0.1

4 结论

本文针对含多间隙弹性约束机械振动系统的力学模型，研究了模型关键参数对系统动力学特性的影响.

1) 基于多参数耦合、多目标协同仿真分析，通过数值计算，揭示了系统在(ω,δ)-参数平面内的周期冲击振动模式类型、分布规律和分岔特征.结果表明，间隙阈值取值越小，系统表现出越复杂的非线性动力学特性.由于振动系统几何结构带有多重非对称弹性约束，导致系统表现出非对称性的周期冲击振动，系统周期冲击振动的模式类型显示出复杂性和多样性特征.

2) 系统在小间隙且低频域内，随着激振频率或间隙阈值的逐渐减小，系统的相邻基本周期冲击振动的q/1基本周期振动经Real-grazing分岔转迁为稳定的(q+1)/1基本周期振动.或q/1基本周期振动经Bare-grazing分岔引发不稳定的(q+1)/1基本周期振动，并伴随出现(nq+1)/n或2(nq+1)/2n亚谐周期振动等复杂的动力学特性.

3) 随间隙阈值的递减，系统在高频区域出现亚谐周期振动和混沌；在低频区域，系统各类周期冲击振动模式类型和分布规律涌现出越发显著的多样性和竞争性.在低频且小间隙域内，随激励频率或间隙阈值减小，系统各质块的冲击次数(p或q)逐渐增多.当系统冲击次数足够大，系统表现出颤-冲击振动特性.

4) 计算结果揭示了含多间隙弹性约束机械振动系统在基准参数取值下的非线性动力学特性.针对不同功能的机械系统能够确定激励频率和间隙阈值等关键参数的科学匹配范围，实现系统动态特性与功能目标的协同优化.