高峰期公交线路运营策略的演化博弈分析
2021-07-16李引珍
吴 亮,李引珍
(兰州交通大学 交通运输学院,兰州 730070)
城市交通问题(道路拥挤、环境污染、资源消耗等)因小汽车的迅速增长而日趋严重,发展公共交通是解决城市交通问题的有效途径之一[1].对于城市常规公共交通,决定公交线路运营策略是否科学合理的首要标准是发车频率,这将有利于均衡高峰期公交出行需求,提升公交服务水平,提高公交客流分担率.作为公交系统内部的主要参与方,出行者与公交运营者双方均期望采取对自身最有利的策略以获得各自最高的收益,结果往往事与愿违.究其原因,主要有以下两点:1) 在决策时双方并未完全掌握自身及对方的全部信息;2) 双方不具有完备的信息处理能力.
研究发现[2-3],动态演化博弈理论既不要求参与人是完全理性的,也不要求完全信息的条件,它将博弈理论分析和动态演化过程分析相结合.目前,演化博弈理论已广泛应用在社会、经济、管理等领域.其中,文献[4-8]均利用演化博弈理论,对共享经济、安居工程、大气污染治理、医患矛盾等方面进行了有益的研究.此外,一些学者已将该理论引入交通领域并初见成效,文献[9]针对出租车随机合乘绕行路径选择问题,构建了出租车合乘路径选择演化博弈模型,研究了合乘路径的演化稳定策略,并分析了合乘演化稳定策略的影响因素;文献[10]考虑不完全信息的影响,运用决策理论和博弈理论设计了基于两阶段选择的综合评价模型,分析了风险偏好对分运人选择策略的影响;文献[11-13]在有限理性的框架下,利用博弈理论对出行者出行方式选择行为展开了研究;文献[14]提出公交价格联动策略演化博弈模型,分析了公交价格策略的演化趋势;文献[15]结合研究区域分析常规公交和地铁的Nash均衡点,并给出合理的最优公共交通出行结构,为有关公交优化提供参考和建议.
综上,虽然现有研究已经关注并将演化博弈理论引入城市公交调度优化研究领域,但是针对公交线路运营策略内在机理的研究有待深入.为此,聚焦公交客流高峰时段,基于演化博弈理论构建出行者与公交运营者之间的非对称演化博弈模型,研究双方的演化博弈行为达到稳定均衡的过程,仿真分析各自策略选择的影响因素,寻找演化稳定策略(evolutionary stability strategy,ESS),进而探究二者的策略互动机制和内在影响机理.
1 非对称演化博弈模型
1.1 模型假设
为简化模型,作以下假设:
假设1将公交线路发车频率分为高低两类.
假设2将出行者分为公交出行者与非公交出行者.
假设3认为政府向公交运营者补贴S采取总价包干形式,与客流分担率无关.
假设4公交票价一票制,固定为1元.
1.2 非对称演化博弈模型
建立出行者与公交运营者的双方非对称演化博弈模型,如表1所列.

表1 出行者与公交运营者的非对称演化博弈模型Tab.1 Asymmetric evolutionary game model between travelers and public transport operators
1.2.1 符号定义
M策略表示公交线路以高于时段内平均发车频率运营;N策略表示公交线路以低于时段内平均发车频率运营;K策略表示出行者选择公交方式出行;L策略表示出行者选择其他交通方式出行.
C为线路平均运营成本,元;I为现有客流票价收入,元;Cr为因发车频率提高而增加的变动运营成本,元;α为潜在客流分担率;β为损失客流分担率;Cd因发车频率降低而减少的变动运营成本,元;S为政府对公交运营者补贴,元;P为公交出行较其他方式出行节省的固定经济收益,元;Pe为正向感知收益,元;Pc为负向感知收益,元;J为其他交通方式出行者的综合平均收益,元.
1.2.2 模型策略含义
公交出行者分为现有客流与潜在客流.
1) 公交运营者选择M策略:
此时仍选择K策略的公交出行者包含现有客流与潜在客流,认为供给大于需求,候车时间成本小,在车拥挤度低,舒适性好,满意度高,完成行程后在收益P的基础上增加正向感知收益Pe.虽然线路运营成本增长至C+Cr,但是因潜在客流的增加,票价收入随之增长αI.总体表现为公交服务水平提高,吸引力增强,公交客流分担率上升.此背景下选择L策略的出行者仅为非公交出行者.根据文献[1]调查,该群体时间敏感度较高,常规公交的运行速度不能满足出行者的需求,公交运营策略的调整对其没有影响,利用其他交通方式完成行程获得收益J.
小结:此背景下加强了现有客流的出行意愿,刺激了潜在客流发生转移.
2) 公交运营者选择N策略:
此时仍然选择K策略的公交出行者仅为现有客流,由于发车频率降低,乘客候车时间成本提高,在车拥挤度逐渐提高,舒适度下降,乘坐体验变差,完成行程导致Pc增加.
此背景下选择L策略的出行者中,包含既定非公交出行群体与损失客流,后者由于公交吸引力降低导致公交客流出现流失情况,总体分担率较原水平降低β比例.非公交出行者完成出行获得平均收益J.虽然公交线路票价收入降低,但是运营成本Cd相应减少.
小结:现有公交客流的出行意愿逐渐削减,甚至出现流失情况.
1.3 复制动态系统
为清晰地掌握双方各自不同策略间的演化形势,构建双方复制动态系统.其中,出行者选择K策略的比例为x,选择L策略的比例为1-x;公交运营者采取M策略的比例为y,采取N策略的比例为1-y.建立双方复制动态方程如下[2]:
1.3.1 出行者复制动态方程
Pm1=(P+Pe)y+(P-Pc)(1-y)=(Pe+Pc)y+P-Pc,
(1)
Pm2=Jy+J(1-y)=J,
(2)
(3)
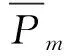
根据以上公式,得到出行者复制动态方程如下:
(4)
F′(x)=(1-2x)[(Pe+Pc)y+P-Pc-J].
(5)
1.3.2 公交运营者复制动态方程
Pn1=x[(1+α)I+S-C-Cr]+(1-x)(I+S-C-Cr)=xαI+I+S-C-Cr,
(6)
Pn2=x(I+S-C+Cd)+(1-x)[(1-β)I+S-C+Cd]=xβI+(1-β)I+S-C+Cd,
(7)
(8)
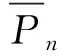
根据以上公式,得到公交运营者的复制动态方程如下:
(9)
F′(y)=(1-2y)[x(α-β)I+βI-Cr-Cd].
(10)
2 双方策略演化
2.1 乘客群体的策略演化
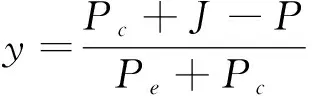
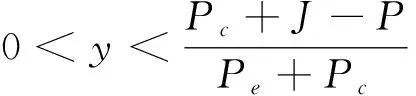
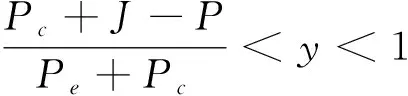
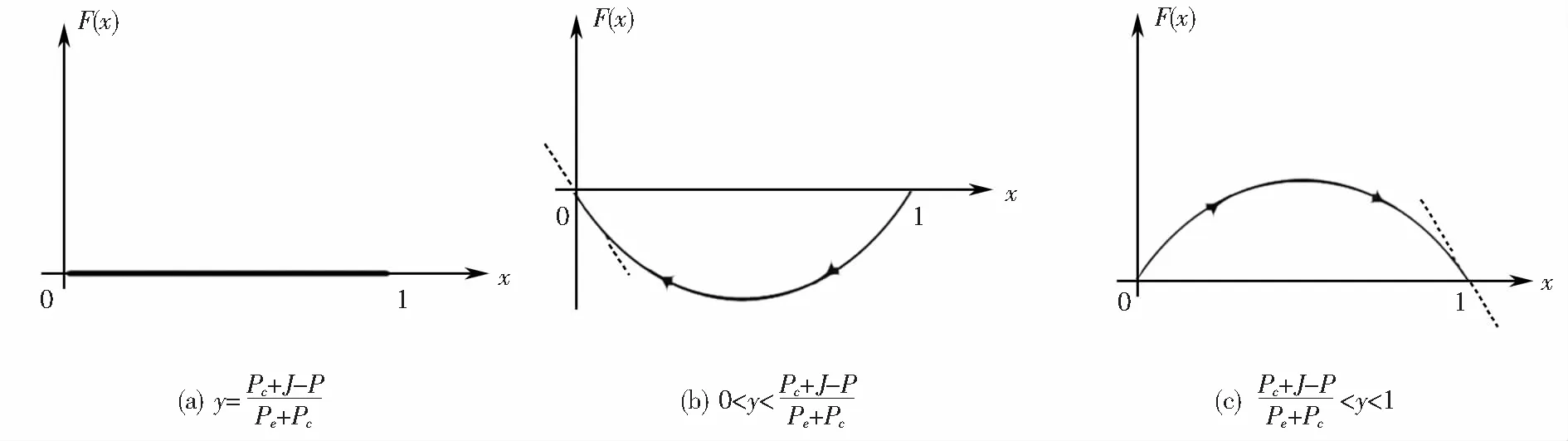
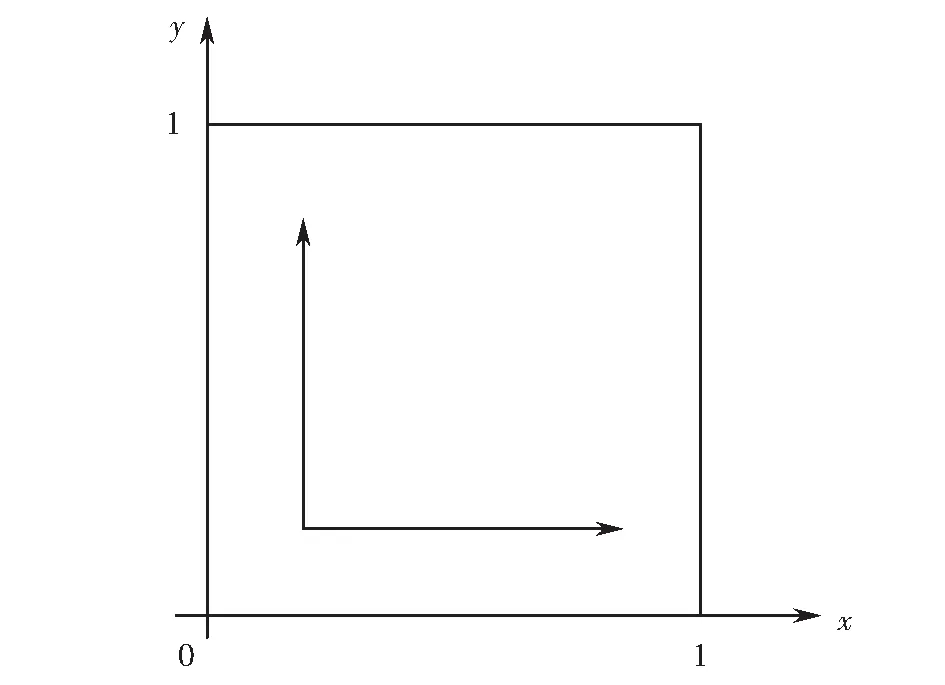
图1 出行者群体的复制动态相位图Fig.1 Replicator dynamics phase diagram of traveler group
2.2 公交运营者的策略与演化



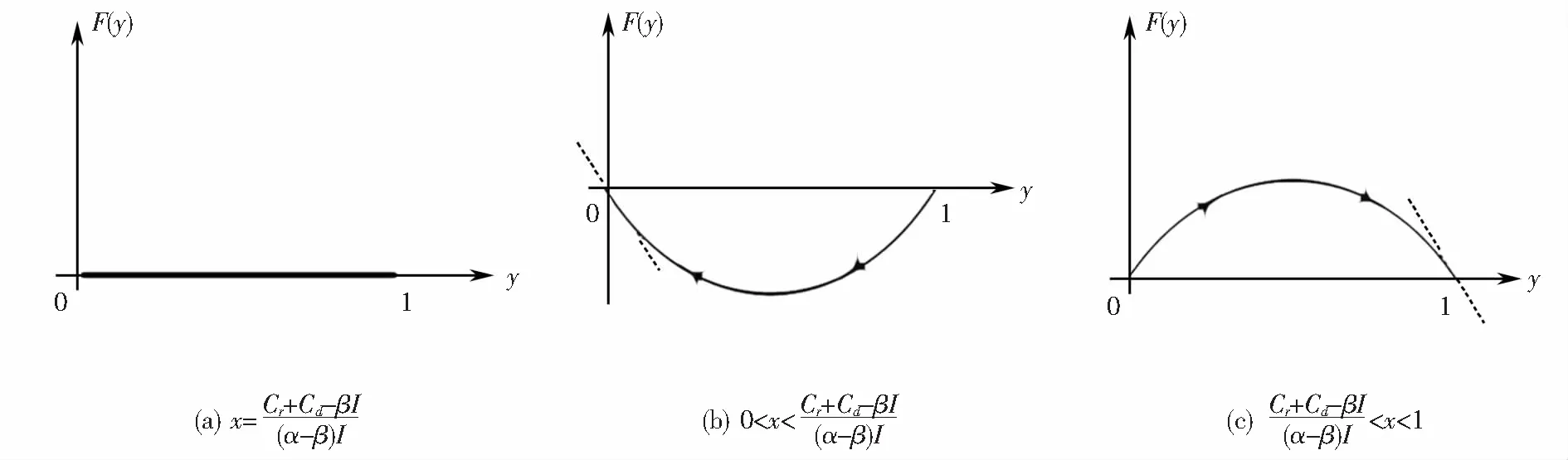
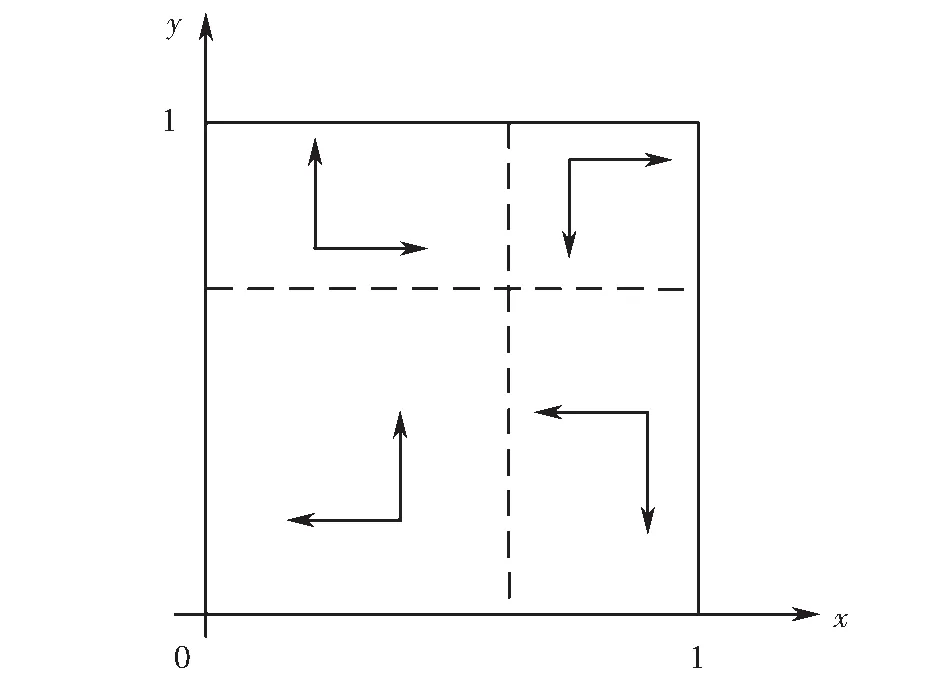
图2 公交运营者的复制动态相位图Fig.2 Replicator dynamics phase diagram of public transport operators
3 动态复制系统策略分析
虽然以上演化策略能够解释乘客群体和公交运营者双方各自的策略演化过程,但是针对双方共同参与的动态复制系统演化如何达到稳定均衡无法说明.
3.1 均衡点稳定性分析

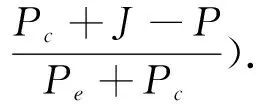
在以上系统平衡点中,存在稳定平衡点、不稳定平衡点及鞍点,雅可比矩阵能够很好地解决可微方程与给出点的最优线性逼近问题.因此,构建动态复制系统的雅可比矩阵[3]:
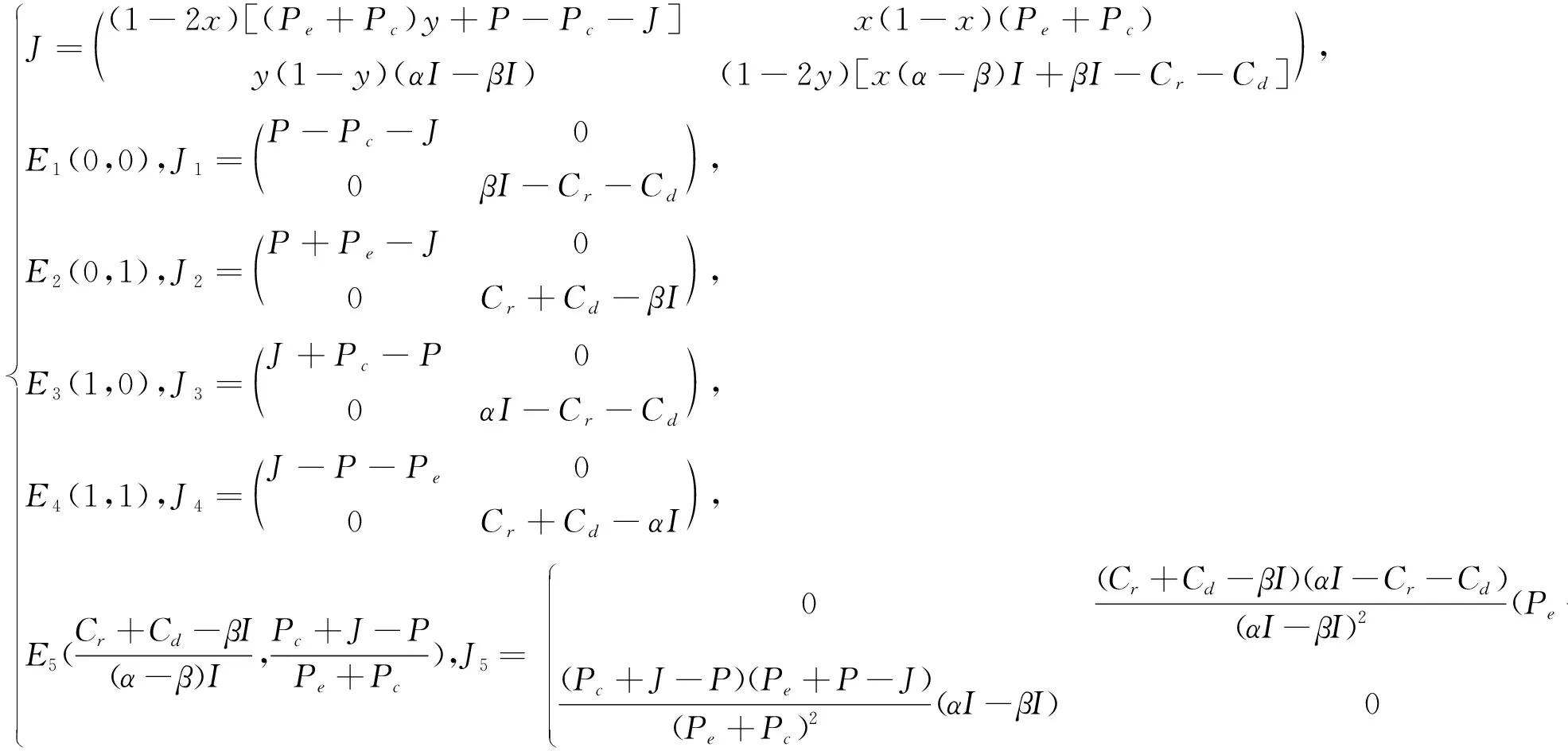
(11)
现通过计算雅可比矩阵的行列式det(J)与迹tr(J),进而判定各平衡点的稳定性,结合Cr+Cd-βI、Cr+Cd-αI、α与β之间的大小组合关系,分别考虑以下8种情形:
情形1:当Cr+Cd-βI>0、Cr+Cd-αI<0、α>β时,各均衡点稳定性分析如表2所列.
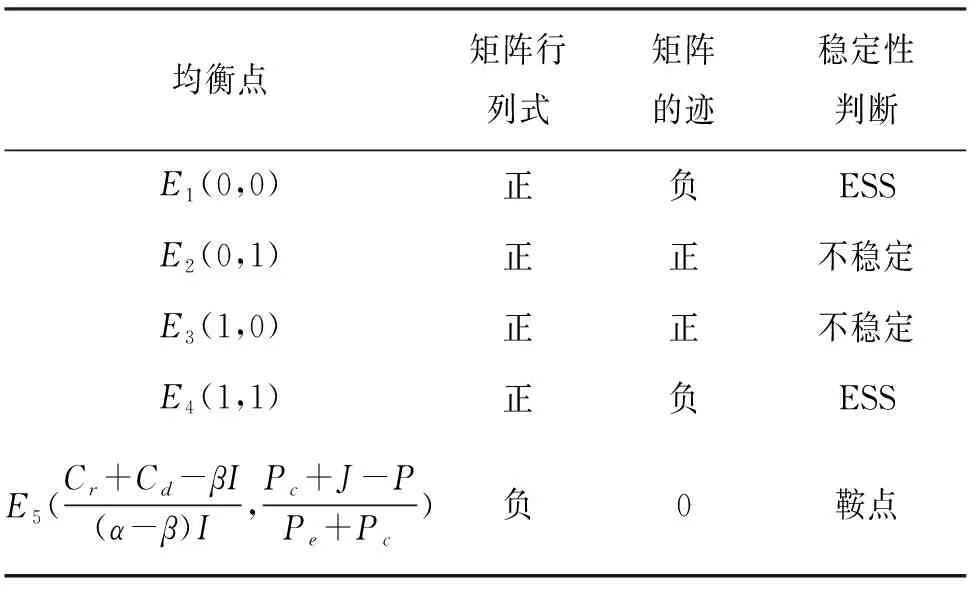
表2 情形1下的演化博弈均衡点稳定性Tab.2 Stability of equilibrium point of evolutionary gameunder condition 1
情形2:当Cr+Cd-βI>0、Cr+Cd-αI>0、α>β时,各均衡点稳定性分析如表3所列.

表3 情形2下的演化博弈均衡点稳定性Tab.3 Stability of equilibrium point of evolutionary gameunder condition 2
情形3:当Cr+Cd-βI<0、Cr+Cd-αI<0、α<β时,各均衡点稳定性分析如表4所列.
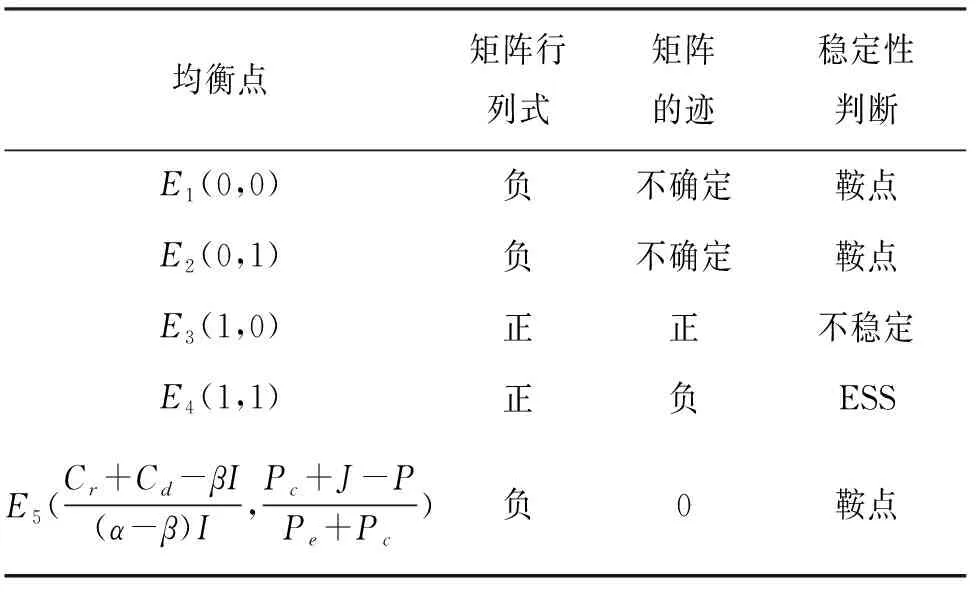
表4 情形3下的演化博弈均衡点稳定性Tab.4 Stability of equilibrium point of evolutionary gameunder condition 3
情形4:当Cr+Cd-βI<0、Cr+Cd-αI>0、α<β时,各均衡点稳定性分析如表5所列.

表5 情形4下的演化博弈均衡点稳定性Tab.5 Stability of equilibrium point of evolutionary gameunder condition 4
情形5:当Cr+Cd-βI>0、Cr+Cd-αI>0、α<β时,各均衡点稳定性分析如表6所列.
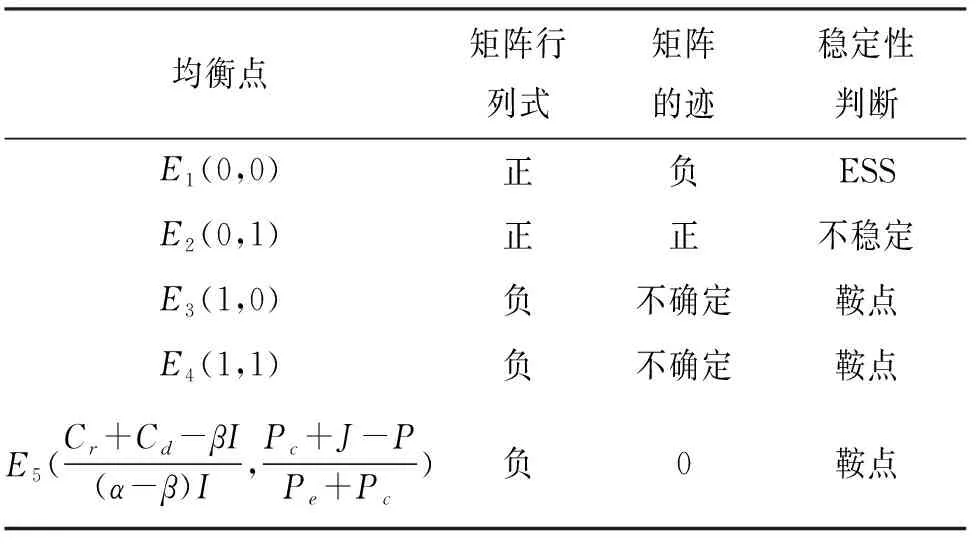
表6 情形5下的演化博弈均衡点稳定性Tab.6 Stability of equilibrium point of evolutionary gameunder condition 5
情形6:当Cr+Cd-βI<0、Cr+Cd-αI<0、α>β时,各均衡点稳定性分析如表7所列.
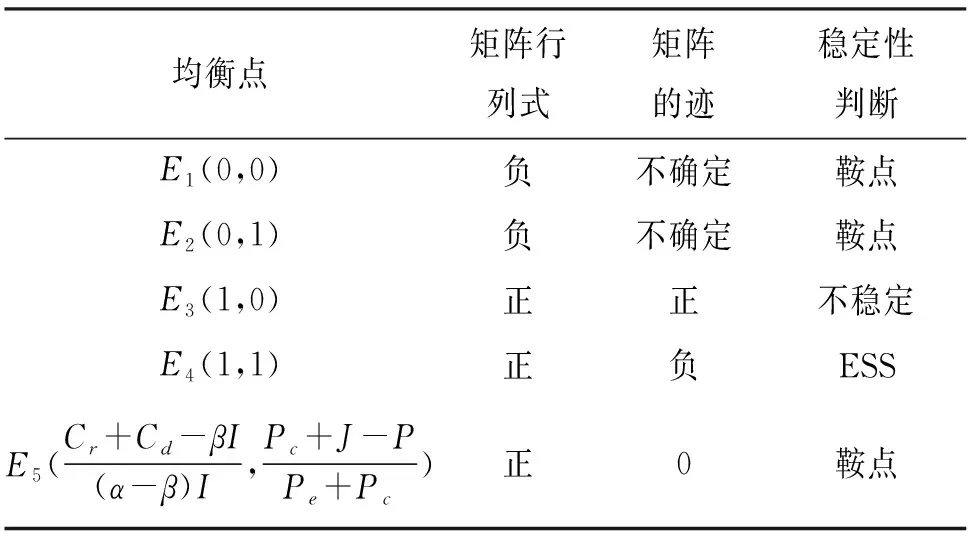
表7 情形6下的演化博弈均衡点稳定性Tab.7 Stability of equilibrium point of evolutionary gameunder condition 6
情形7:当Cr+Cd-βI>0、Cr+Cd-αI<0、α<β时,相互矛盾不成立.
情形8:当Cr+Cd-βI<0、Cr+Cd-αI>0、α>β时,相互矛盾不成立.
3.2 系统演化路径分析
为进一步明确分析双方得益,现简化非对称演化博弈模型如表8所列.

表8 出行者与公交运营者的非对称演化博弈简化模型Tab.8 A simplified model of asymmetric evolutionary gamebetween travelers and public transport operators
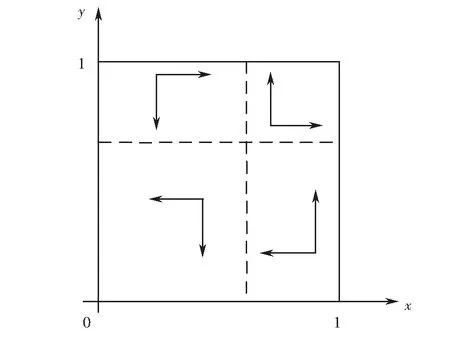
图3 情形1下的系统演化路径Fig.3 System evolution path under condition 1
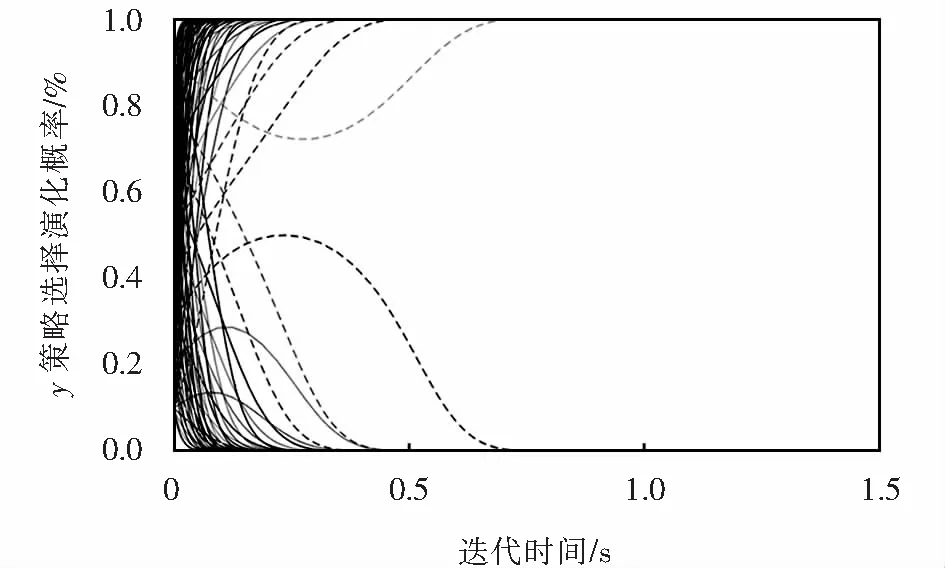
针对情形2,出行者群体的选择对公交运营者的决策影响单一,公交运营者的收益均为B 图4 情形2下的系统演化路径Fig.4 System evolution path under condition 2 图5 情形3下的系统演化路径Fig.5 System evolution path under condition 3 针对情形4,出行者与公交运营者的不同策略组合关系下,动态复制系统的演化路径均不相同,此时不存在ESS,系统演化路径如图6所示. 图6 情形4下的系统演化路径Fig.6 System evolution path under condition 4 针对情形5和情形6,系统演化路径分别与情形2和情形3一致,说明α与β关系在动态演化系统内相对独立,对演化路径没有产生影响. 以上,当公交线路以M策略运营时,出行者群体收益均有A>F;当公交线路以N策略运营时,出行者群体收益均有D 由于篇幅有限,仅针对情形1进行仿真研究.设J=0.9,P=1,Pc=0.4,Pe=0.1,Cr=0.05*I,Cd=0.02*I,α=8.1%,β=5%,利用MATLAB软件进行计算仿真. x与y不同初始概率组合对双方策略选择演化结果产生影响.经计算,当x低于0.645、y低于0.6时,x与y均明显趋向0演化;当x高于0.645、y高于0.6时,x与y均明显趋向1演化,如图7~8所示. 图7 x策略选择演化博弈仿真结果Fig.7 Evolutionary game simulation results of x strategy selection 图8 y策略选择演化博弈仿真结果Fig.8 Evolutionary game simulation results of y strategy selection 公交运营者选择M策略,出行者选择K与L不同策略的收益差为A-F;公交运营者选择N策略,出行者选择K与L不同策略的收益差为P-D.考虑公交运营策略差异的影响,为高峰期吸引更多客流乘坐公交出行,提高A-F收益,降低P-D差值,基于公交运营策略扩大出行者的收益变化值A-F-P+D,进而加强公交出行者的出行意愿.此外,扩大出行者选择公交出行与其他交通方式的收益差A-P,能够减少客流流失,刺激潜在客流转移,能够加快出行者策略在演化博弈系统中达到ESS的收敛速度. 出行者选择K策略,公交运营者选择M与N不同策略的收益差为B-E;出行者选择L策略,公交运营者选择M与N不同策略下的收益差Q-G.为保证客流正常运送前提下公交运营者获得更大收益,通过提高B-E收益,降低Q-G差值,基于出行者策略扩大公交运营者的收益变化值B-E-Q+G,通过控制公交线路单位班次运营成本、增加运营班次数量等方法,积极促使公交运营者改善运营策略,提升运营效益,能够加快公交运营策略在演化博弈系统中达到ESS的收敛速度. 仿真结果与情形1中的系统演化路径演变过程相符,且y群体相较x群体演化速度更快,这与鞍点位置有关.x、y值的大小均受到公交运营者与出行者双方选择策略初始概率的影响. 面向公交客流高峰时段,将可变的发车频率作为公交运营者的选择策略,构建了出行者与公交运营者的双方非对称演化博弈模型,期间采用复制动态方程分析了演化路径及相关均衡点的稳定性,研究了不同情形下的演化博弈稳定策略,利用复制动态图更加清晰地展现了参与者双方的演化博弈行为达到稳定的过程,有针对性地仿真分析了双方策略选择的影响因素,对加快二者构成的演化博弈系统达到ESS的收敛速度具有帮助,以期为公交运营管理决策提供理论支持. 科学的公交补贴机制对于城市公交系统优化具有直接影响.本文在建立模型时仅考虑单一固定的公交补贴方式,在未来研究中应进一步考虑与公交客流结构相关的政府补贴机制,使研究结果更加符合实际.

4 数值仿真
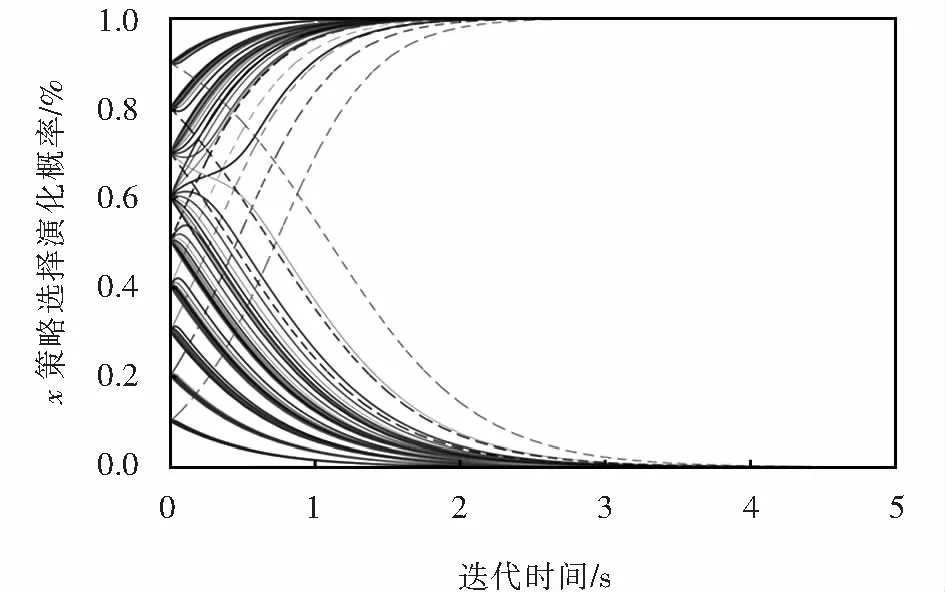
4.1 x值的影响因素
4.2 y值的影响因素
5 结论
