多智能体系统指定时间双向编队控制

周 媛，刘永芳，马生昌，赵 宇

（西北工业大学自动化学院，西安 710129）

1 引 言

随着计算机、互联网、微电子等新科技在军事方面的不断发展，现代战争形态逐渐从“机械化”向“信息化、智能化”转变，无人系统作战技术已成为各国争相发展的关键技术。而传统的单机作战由于其探测能力、抗扰能力、打击能力等方面的局限性导致其无法适应现代化战争环境的复杂性、作战任务的艰巨性，因此，无人系统集群作战将成为未来战争的主要作战方式[1-3]。在此背景下，对基于多智能体的无人系统进行协调控制这一关键技术就显得尤为重要。

多智能体系统是近年来新兴的一个比较热门的研究方向，它是指由一系列信息交互的智能体组成的群体系统，其内部的各智能体可通过相互感知、相互通信等方式，完成单个智能体所不能完成的大规模的复杂的特定任务。分布式控制是多智能体系统协调控制的主要方式，其仅依赖每个智能体与其邻居智能体间的状态信息交互对系统实行控制。分布式控制的优势在于完成任务的同时也克服了集中式控制产生的计算量与能耗较大的缺陷，具有更高的应用价值。作为多智能体系统协同控制的热点研究问题，编队控制要求系统中的每个个体在执行任务过程中能保持一定的几何形态，以适应其所处的环境约束。比如在大型物资运输过程中，对运输车辆所处的位置有一定的要求，以满足运输过程的稳定和负载平衡等[4-5]。

近年来，大量的国内外学者对多智能体系统分布式编队控制进行了深入的研究，并且取得了丰硕的研究成果。文献[6]基于人工势能场，对轮式机器人模型系统领航—跟踪问题进行了深入研究，提出了一种新型的“行星–卫星”式避障算法。但该算法仅能保证系统渐近收敛，即当时间接近正无穷大时，跟踪者才能收敛到其领航者的轨迹。然而，在实际应用时，对任务时间总是有着一定的要求，人们期望系统能在给定的时间限制之前达到控制目标。因此，Cortés[7]基于一阶积分器系统提出了有限时间控制，并将其应用于梯度系统实现多智能体系统有限时间一致性控制。自此，出现了多种多样的有关多智能体有限时间控制问题，如有限时间跟踪问题[8-9]，多卫星有限时间编队问题[10-13]和自适应有限时间同步问题[14]。但是，有限时间控制所得到的收敛时间常与初始状态相关，如果不能预先获得系统的初始状态，那么控制器将会失去其效用。于是又提出了固定时间算法[15-17]来解决这个问题。该算法主要依赖控制器的参数，计算出其收敛时间的上界，所以，固定时间算法的收敛时间通常具有一定的保守性。为克服以上算法的缺陷，本文提出了一种指定时间控制算法，使系统的收敛时间仅取决于用户的设定值。

需要指出的是，上述文献的研究均是基于智能体之间为协同合作关系假设得出的，而实际中不同个体间既存在合作关系又存在竞争关系，这样的考虑更为普遍。文献[18]正是基于这样的想法，将智能体间的信息交互用图论进行描述，其中正的边权重可以表示个体间为合作关系，负的权重可表示智能体间的竞争关系。基于这样的模型，Altafini[18]提出了“双向一致性”的概念，并给出了多智能体系统实现双向一致性的充要条件。于是，文献[19-20]分别研究了一阶积分器和二阶积分器多智能体系统双向一致性编队问题，其要求智能体能以分组的形式实现各组的编队构型，并且每组智能体能以特定的队形、相反的方向进行运动。除此之外，文献[21]针对二阶非线性多智能体系统双向编队问题，设计了脉冲控制器及状态反馈控制器，实现脉冲控制机制下系统双向编队目标。但目前，在多智能体系统双向编队控制这一问题上的研究成果还远远不足，还需从不同的控制算法、不同的控制系统对多智能体系统双向编队控制进行较为深入的探讨。

因此，本文研究了具有一般线性动力学的多智能体系统的指定时间双向编队问题。利用庞特里亚金极大值原理和运动规划技术，提出了双向编队控制算法，使系统能够在指定时间内实现双向编队。与现有的多智能体系统分布式控制结果相比，本文的贡献主要体现在以下三个方面：首先，提出了一种变增益的指定时间控制律，系统的收敛时间可由用户任意指定，克服了传统的有限时间控制对初始状态的依赖性和固定时间控制导致的保守性的缺点[7-17]。其次，与现有的基于完全协同拓扑[6-17]的文献不同，本文研究的拓扑结构同时含有协同和竞争作用。但本文提出的控制算法同样适用于解决传统的非负图的指定时间一致性编队问题。最后，值得注意的是，本文提出的控制器仅依赖离散的采样时刻多智能体的状态，也就是说该算法并不需要系统实时通信，仅要求系统在采样点处满足一定的通信条件。因此，该算法能够减轻网络的通信负担，降低其对网络通信能力的要求。

2 背景知识

2.1 记号说明

本文使用标准符号。文中，用R表示实数集，Rn表示n维的实列向量集， Rm×n表示m×n的实矩阵集。那么， 1n∈Rn表示元素为1的n维列向量，In∈Rn×n表示单位矩阵。d iag {m1,m2,… ,mn}表示以m1,m2,… ,mn为对角元素的对角矩阵。⊗表示克罗内克积，表示欧几里得范数， det ()表示行列式， sgn ()表示符号函数，表示绝对值符号。对于一个矩阵M∈Rn×n来说，M≻0意味着M的所有元素均非负，若其同时满足M1n=1n，则称M为随机矩阵。

引理 1.对于随机矩阵M，若其所有特征值满足则称其为SIA（Stochastic，Indecomposable, Aperiodic）矩阵。并且M具有如下性质：其中y∈Rn表示元素均非负的n维列向量[22]。

2.2 图论知识

基于图论知识，本文使用带符号的有向图G = ( V,E,A)来表示智能体间通信拓扑结构，其中点集 V ={1 ,2,…,N}表示N个智能体，边集E = {Eij= (i,j)} 表示智能体之间的信息流，A= [aij] ∈RN×N表示图G 的加权邻接矩阵。边集元素表示从有信息流从j节点传递给i节点，从而A中相应的元素αij≠ 0，反之，αij=0；如果αij＜ 0表示j节点和i节点之间为竞争关系，αij＞ 0表示j节点和i节点之间为合作关系。本文不考虑带有自环的拓扑结构，因此，αii= 0。符号 adj(i)表示智能体i的邻居集合。那么，图的拉普拉斯矩阵可以定义为L=[lij]，其中若图G 中存在一个点i可以向图中其他所有的点传送信息，那么称i节点为根节点，称图G 含有生成树。

图G 称为结构平衡图当且仅当点集V分为完全没有交集的两个子集并且同时满足以下条件：（1） V1∪ V2=V， V1∩ V2=∅；（2）αij＜ 0, ∀i,j∈Vk；αij＞ 0, ∀i∈Vk,j∈V3-k，其 中k∈{ 1 ,2}。

引理2.如果图G 为结构平衡图，L为其相应的拉普拉斯矩阵，那么，一定存在对角矩阵Υ=diag {γ1,γ2,… ,γn}，使ΥLΥ≻0，其中γi∈ {1 ,-1 }[18]。

2.3 系统模型

考虑由N个一般线性动力学组成的多智能体系统，其动力学方程可以描述为

定义编队误差ei(t) =xi(t)-hi，其中hi∈Rn为第i个智能体的编队向量，那么，系统(1)的指定时间双向编队目标可以表述如下。

定义 1.对多智能体系统(1)，如果对于任意的初始状态xi(t0)及人为指定的时间T，都有

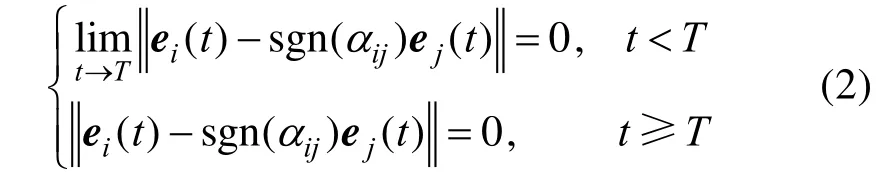
则称系统(1)实现了指定时间双向编队。

注 1.式(2)所表述的指定时间双向编队问题要求不同组的智能体的状态分别实现自己的编队构型，并以不同的方向分别运动。具体来讲，当智能体i和智能体j属于同一子集时，αij＞ 0，那么即i和j运动方向相同；当i和j属于不同子集时，即i和j运动方向相反。显然，当hi=hj= 0时，式(2)描述的控制目标可以重新表述为“指定时间双向一致性”。因此，得出结论：“双向一致性”是“双向编队”的特例。

为了实现系统“指定时间双向编队”的控制目标，本文做出如下假设。

假设1.多智能体系统(1)能控；

假设2.带符号的有向拓扑结构G为含有一棵生成树的结构平衡图。

注 2.本文考虑两个组的智能体分别实现各自的编队构型，因此系统(1)满足能控条件仅是对线性系统一个比较基本的条件。另外，假设2要求拓扑结构中有足够的信息流，其能从网络中的某个节点流向其他节点；此外，智能体实现双向编队还需满足分组条件。综其所述，本文所给的假设1和假设2是必要且可行的。

引理 3.若多智能体系统(1)满足假设1，那么当t≠t0时，有[10]

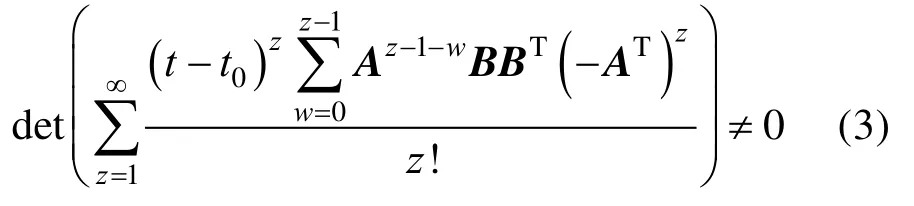
引理 4.记若拓扑结构G满足假设2，那么图G的拉普拉斯矩阵L满足：

其中：lii为拉普拉斯矩阵L的对角元素。

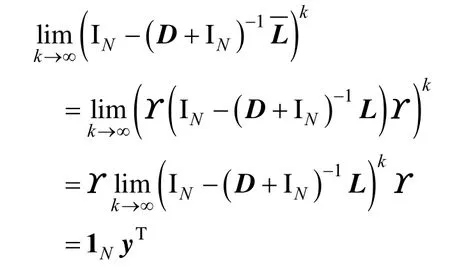
因此，式(4)成立。

3 指定时间双向编队控制算法

3.1 指定时间双向编队控制器设计

基于非周期采样算法，本文提出非周期采样时间序列为

另外，在运动规划技术和SIA矩阵的性质下，第i个智能体在第k+1步的终端状态约束为

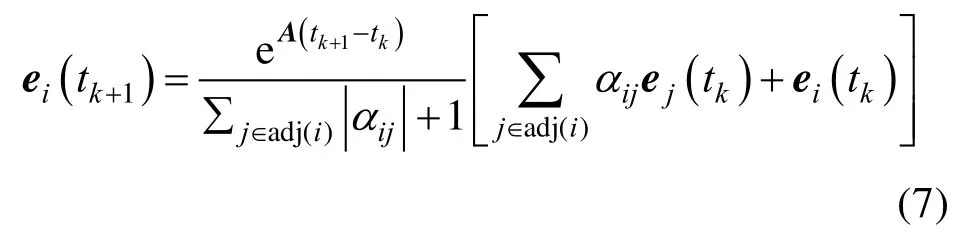
因此，对式(1)、(6)应用庞特里亚金极大值原理，构造式(6)的哈密顿函数：

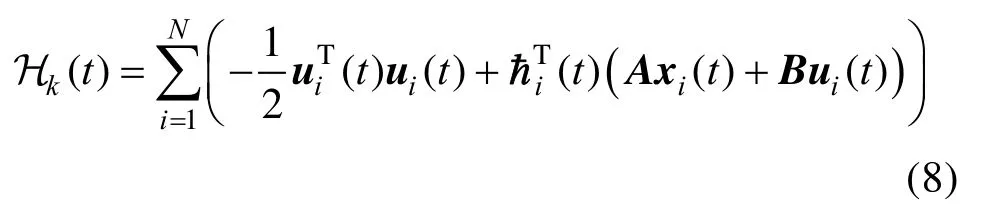
其中：ħi(t)为协态变量。继而，式(8)分别对hi,xi和ui求偏导，有

其中，式(9c)为式(8)存在极值的必要条件。联立式(9a)、(9b)，可发现其为一线性矩阵方程组。对其从tk至tk1+进行积分，有

其中：

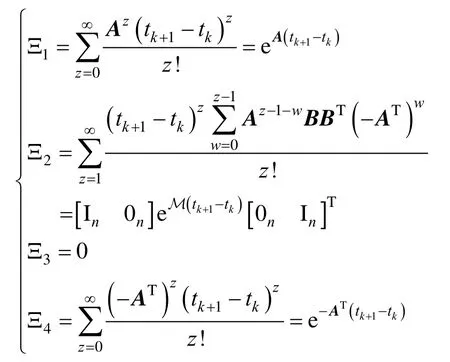
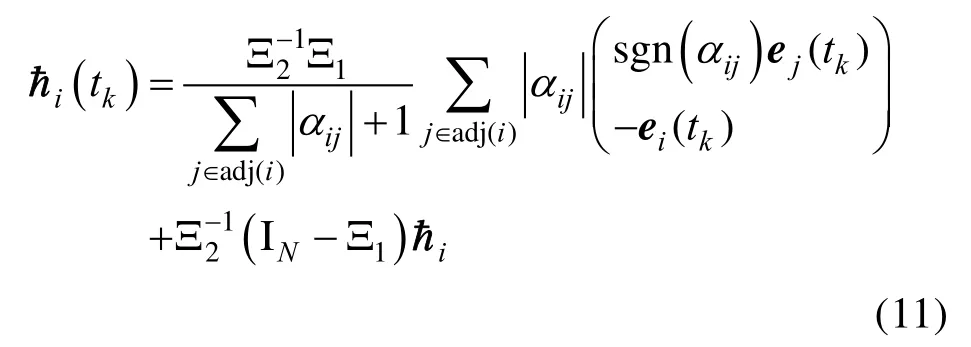
3.2 指定时间双向编队收敛性分析

定理1.若系统(1)满足假设1且拓扑结构G满足假设 2，那么，控制器(12)按照时间序列式(5)进行采样，能够保证系统(1)实现指定时间双向编队。

证.首先，证明在控制器(12)作用下，多智能体系统(1)的采样状态收敛，即

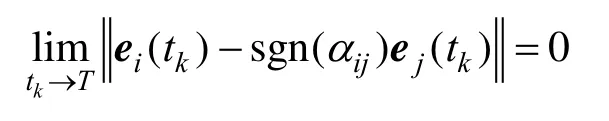
将式(12)代入系统，并对其从t至tk1+进行积分，有

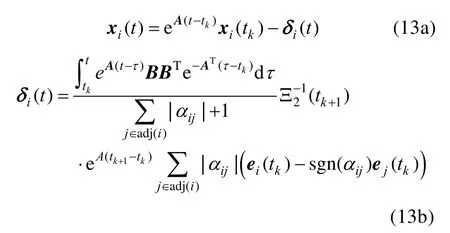
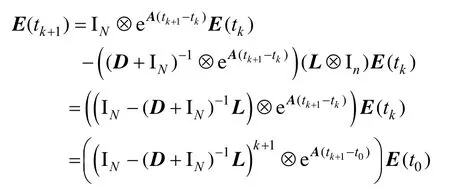
根据引理4中SIA矩阵的性质，有

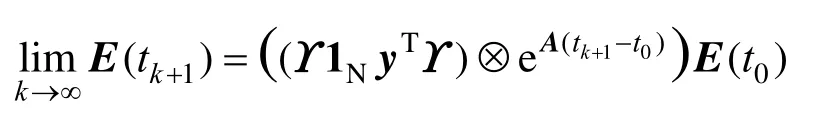
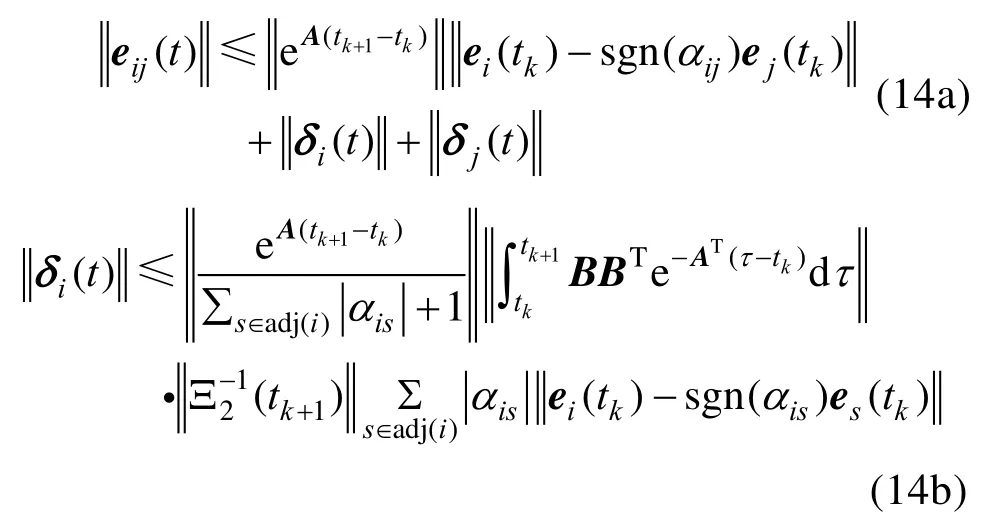
综上所述，控制器(12)能够使系统(1)实现指定时间双向编队。

注 3.文中设计的控制器(12)取决于时间序列间隔tk+1-tk的大小，由于采样时间序列是非周期的，因此控制器(12)的增益是时变的。另外，控制器的大小仅取决于离散的采样时刻状态大小，而不需系统满足实时通信，从而减轻网络的通信负担，降低其对网络通信能力的要求。

注 4.控制器(12)可实现多智能体系统(1)实现指定时间双向编队控制。与文献[7-17]相比，本文设计的控制器主要优势在于系统的收敛时间可事先人为指定，而不依赖系统的初始状态，同时也不具有保守性。

注 5.由于文中提出的控制器适用于结构平衡的拓扑结构，而传统的无符号拓扑结构是一类特殊的结构平衡图，其中一个子集为空。因此，将本文的控制器应用于传统的拓扑结构上时可实现一般的指定时间编队控制。

注 6.显然，采样序列(1)的收敛性在控制系统实现指定时间编队的过程中发挥着重要作用，在此，可选取采样时间间隔为k= 1,2,…}，其以多项式速率收敛至T。另一个可选取的采样时间间隔为k= 1,2,…}，其以指数速率收敛到T。

但是，注意到在以上采样序列作用下，控制器(12)会在有限时间内产生无数次采样，即产生了芝诺效应。为解决这一问题，通常会采取一个误差上界来避免此现象，即：当时，认为其已经实现了指定时间双向编队。由此，可以推导出采样频率的上界：

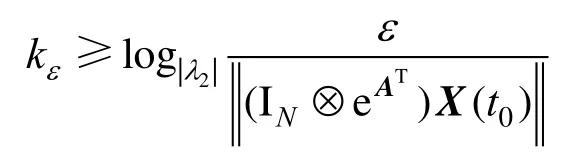
因此，修正后的采样间隔序列为

4 仿真结果及分析

在这一部分，我们考虑6个动力学为二阶积分器类型的智能体的指定时间二分编队控制问题的数值仿真。为便于刻画其在指定时间的收敛性，本文仅考虑x-y平面内智能体实现编队，即则系统的动力学可如式(16)所示：

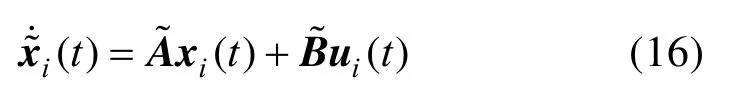
其中：

显然，式(16)描述的系统一定为能控系统，即满足假设1。智能体间的通信拓扑结构可由图1来描述，其满足假设 2，其中V1= {1 ,2,3}，V2= {4 ,5,6}。

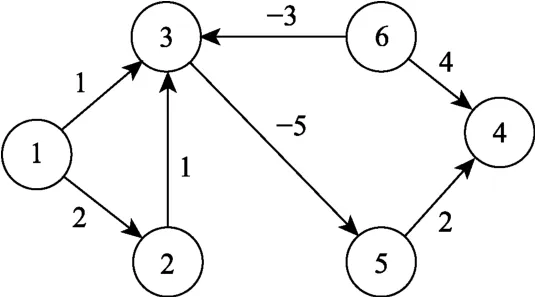
图1 6个智能体的通信拓扑结构Fig.1 The communication topology with 6 agents

为了能够以一个三维视图（时间–二维平面）的方式显示指定时间算法的有效性，假设智能体在高度方向上保持一致，则相应的编队队形为二维平面图形。指定智能体最后的编队队形为两正三角形，则相应的编队向量可以给定为指定系统的收敛时间为T=8以及编队误差界限ε= 10–3，对其进行仿真，结果如下所示。

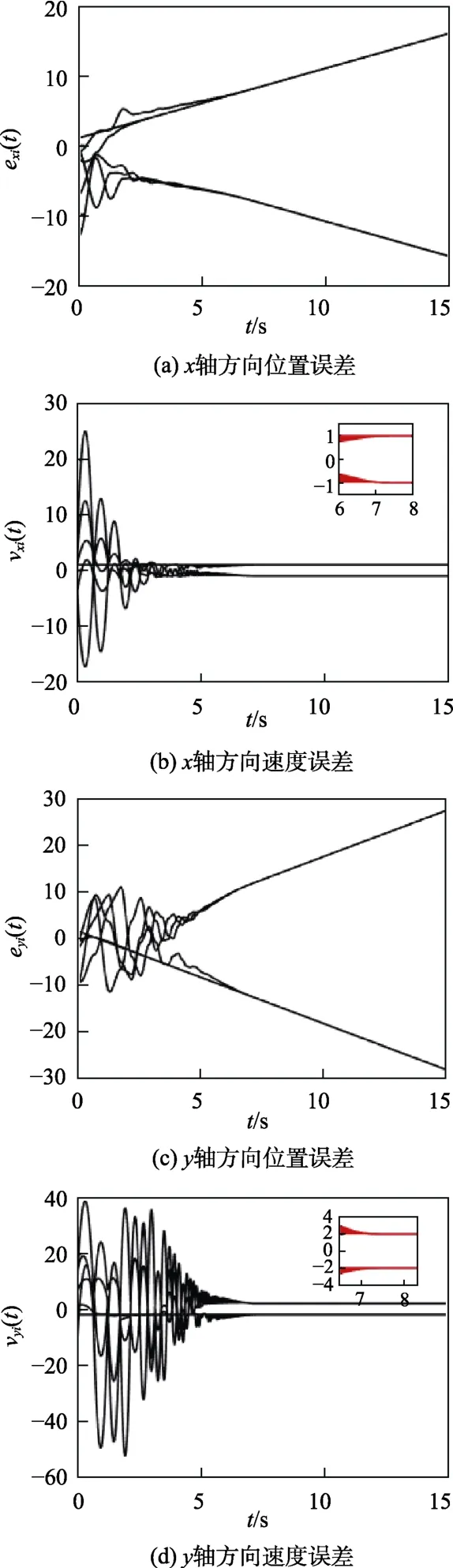
图2 智能体位置误差和速度误差Fig.2 The position errors and velocity errors of agents

图3刻画了6个智能体的运动轨迹，并绘制了系统在t=8和t=15时两组智能体的编队队形。显然，属于不同子集的智能体实现各自编队队形之后便朝着相反的方向进行运动，即实现了双向编队。

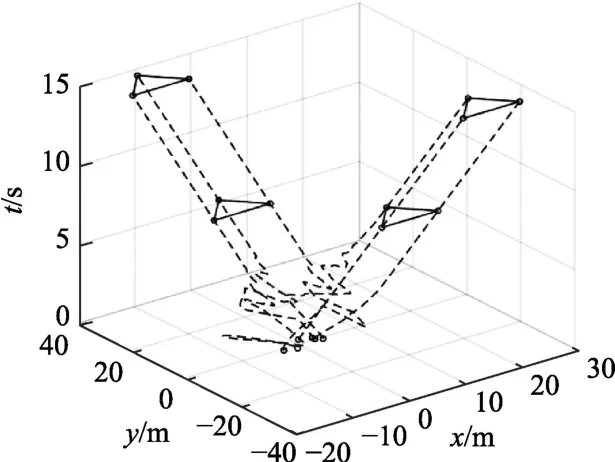
图3 6个智能体的飞行轨迹Fig.3 The real flight trajectories of 6 agents

5 结 论

计算机及网络技术的发展，推动了现代战争向集群作战方式转变，同时也为多智能体系统技术的应用提供了一个广阔的平台。本文针对作战过程中无人系统的编队问题，利用庞特里亚金极大值原理，设计了一类分布式双向编队控制器，解决了一般线性动力学多智能体系统指定时间双向编队问题，并且通过数值仿真证明了控制器的有效性，为无人系统的编队飞行提供了潜在的应用前景。

后续还可围绕文中所提算法进行以下研究：

（1）针对领航者—跟随者网络编队问题，设计相应的分布式控制器使系统实现指定时间收敛。

（2）本文控制器依靠状态反馈来实现多智能体系统指定时间双向编队，但当网络受到攻击时，智能体间的通信会受到干扰，因此，可以考虑基于输出反馈来实现系统指定时间双向编队控制。