北斗卫星精密星历插值精度研究*

郭忠臣，宋明洋，鲍雅君，崔 磊，张 可

(1. 安徽理工大学地球与环境学院，安徽 淮南 232001；2. 宿州学院环境与测绘工程学院，安徽 宿州 234000； 3. 桂林理工大学测绘地理信息学院，广西 桂林 541006)

2020年6月23日，北斗卫星导航系统全球组网完成，标志着我国的北斗卫星导航系统正式走向世界并为全球服务。定位是卫星导航系统服务社会的一个重要功能，而高精度定位所需的卫星位置一般通过精密星历获得，国际GNSS服务组织(International GNSS Service, IGS)发布的精密星历历元间隔一般为15 min或5 min，无法满足实际需求，为获得任意时刻卫星的精确位置，需对精密星历进行内插[1-2]。

有较多学者对精密星历的插值进行了研究，使用的插值方法主要有Lagrange插值法、牛顿(Newton)插值法、样条函数插值法和切比雪夫(Chebyshev)插值法等[3-7]，但多数是对全球定位系统(Global Positioning System, GPS)卫星的精密星历插值精度进行研究，对北斗卫星导航系统精密星历插值的研究相对较少。与全球定位系统卫星星座不同，北斗卫星导航系统包含地球同步静止轨道卫星、倾斜地球同步轨道卫星和中地球轨道卫星3种轨道类型，各类卫星受插值方法和插值阶次的影响也有所区别。截至目前，各轨道卫星分布见表1。当前文献中，多是研究插值方法的精度，并未对3类卫星的插值精度进行分析，而且多选用1颗或3颗(每类卫星1颗)卫星对算法进行实验，数据量较少，对结论的支持相对单薄[8-10]。

表1 北斗卫星导航系统3类轨道卫星分布情况(加粗: 本文实验卫星)Table 1 Distribution of three kinds of orbits of BDS satellites (bold: experimental satellites in this paper)

本文在此前研究的基础上，选用滑动式Lagrange插值法和非滑动式Lagrange插值法对北斗卫星导航系统3类卫星的插值精度进行研究，首先对3类卫星插值精度与插值方法及插值阶次的关系进行研究，分析3类卫星的插值精度以及随插值阶次变化的情况；其次，对低阶次插值情况下，插值误差的统计规律进行分析；最后，对各颗实验卫星在两种方法下的最佳插值阶次进行统计，并对最佳插值阶次下，两种方法的插值精度及3类卫星的最佳插值结果进行对比。由于篇幅限制及考虑部分卫星的数据质量，文中选取伪随机噪声码(Pseudo Random Noise code, PRN)编号在C01～C37之间的32颗卫星数据进行实验，加粗编号为选择的实验卫星。

1 算法原理

1.1 Lagrange插值法

Lagrange插值法可根据已知数据通过插值得到节点内任意位置的数据，若有一系列已知节点x0,x1, …,xn及对应的数值y0,y1, …,yn，则Lagrange插值多项式可表示为[3,11]

(1)

卫星的位置信息中包含X、Y、Z3个坐标分量，则在t时刻3个坐标分量的插值多项式可表示为

(2)

其中，(X(t)，Y(t)，Z(t))为t时刻卫星插值位置；tk(k=0, 1, …,n)为样本点历元；(Xk，Yk，Zk)为tk时刻卫星的位置。

1.2 滑动式Lagrange插值策略

滑动式Lagrange插值法是在传统插值法的基础上将插值区间视为一个可滑动的窗口，在插值过程中令插值区间随待插值点不断移动，使待插值点时刻位于插值区间中心位置[11-12]。传统插值法在应用中易出现 “龙格” 现象，即插值区间端点附近的结果容易出现震荡而导致插值精度较低，滑动式算法仅对插值区间中心位置进行插值，能够避免 “龙格” 现象对精度的影响，进而提高插值精度，但计算量较非滑动式算法大，在实际应用过程中，可综合考虑插值精度和效率，将滑动式与非滑动式两种方法组合使用。

2 实验分析

本文采用2020年5月30日IGS发布的历元间隔为5 min的精密星历作为原始数据，并对原始数据进行分析。依据表1，提取32颗卫星的精密星历，其中每颗卫星包含288个三维坐标位置。为了对两种方法的插值精度及插值阶次进行研究，提取该天内以10 min为时间间隔的坐标作为已知数据，对其余已知时刻的坐标进行插值，并与精密星历进行对比，采用均方根(Root Mean Square, RMS)误差作为精度评价指标。鉴于实验卫星数目较多，且三维坐标的每个方向插值均有误差，同时由于篇幅限制，后面所提到的均方根误差均表示卫星位置综合插值误差，不再单独对各方向的均方根误差进行统计分析。

2.1 3类卫星插值精度与插值方法及插值阶次的关系

为研究非滑动式及滑动式Lagrange插值法中插值阶次对精度的影响情况，我们分别统计了阶次在4～20时的插值精度，结果见图1和图2。为了体现3类卫星在不同插值情况下的精度量级，本文选取每类卫星中的两颗卫星进行插值精度统计，结果见表2和表3。

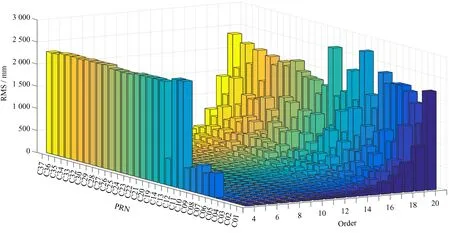
图1 不同插值阶次下非滑动式Lagrange插值法精度统计Fig.1 Accuracy statistics of non-sliding Lagrange interpolation with different interpolation orders

图2 不同插值阶次下滑动式Lagrange插值法精度统计Fig.2 Accuracy statistics of sliding Lagrange interpolation with different interpolation orders

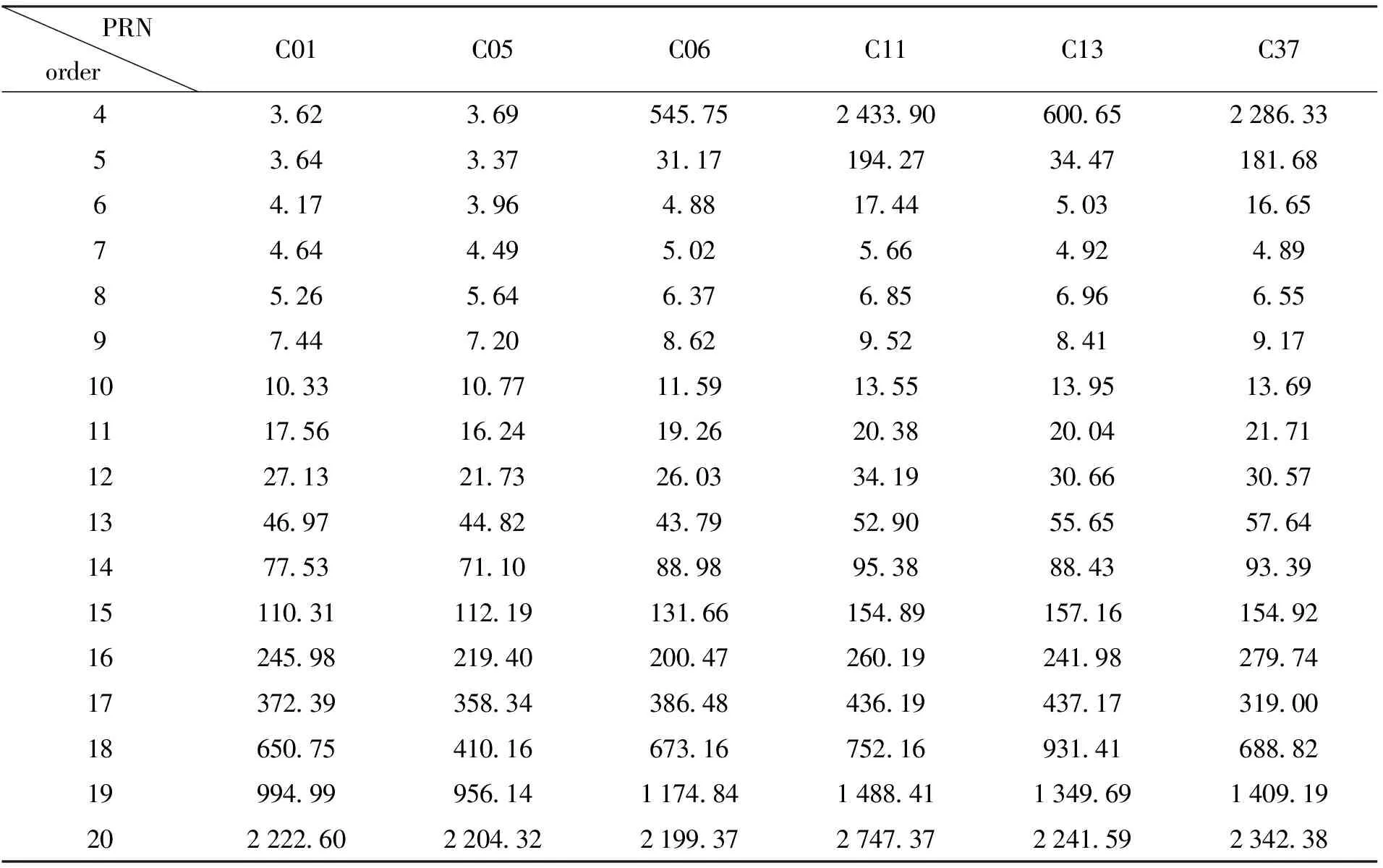
表2 不同插值阶次下非滑动式Lagrange插值法精度统计(单位： mm)Table 2 Accuracy statistics of non-sliding Lagrange interpolation with different interpolation orders (unit: mm)

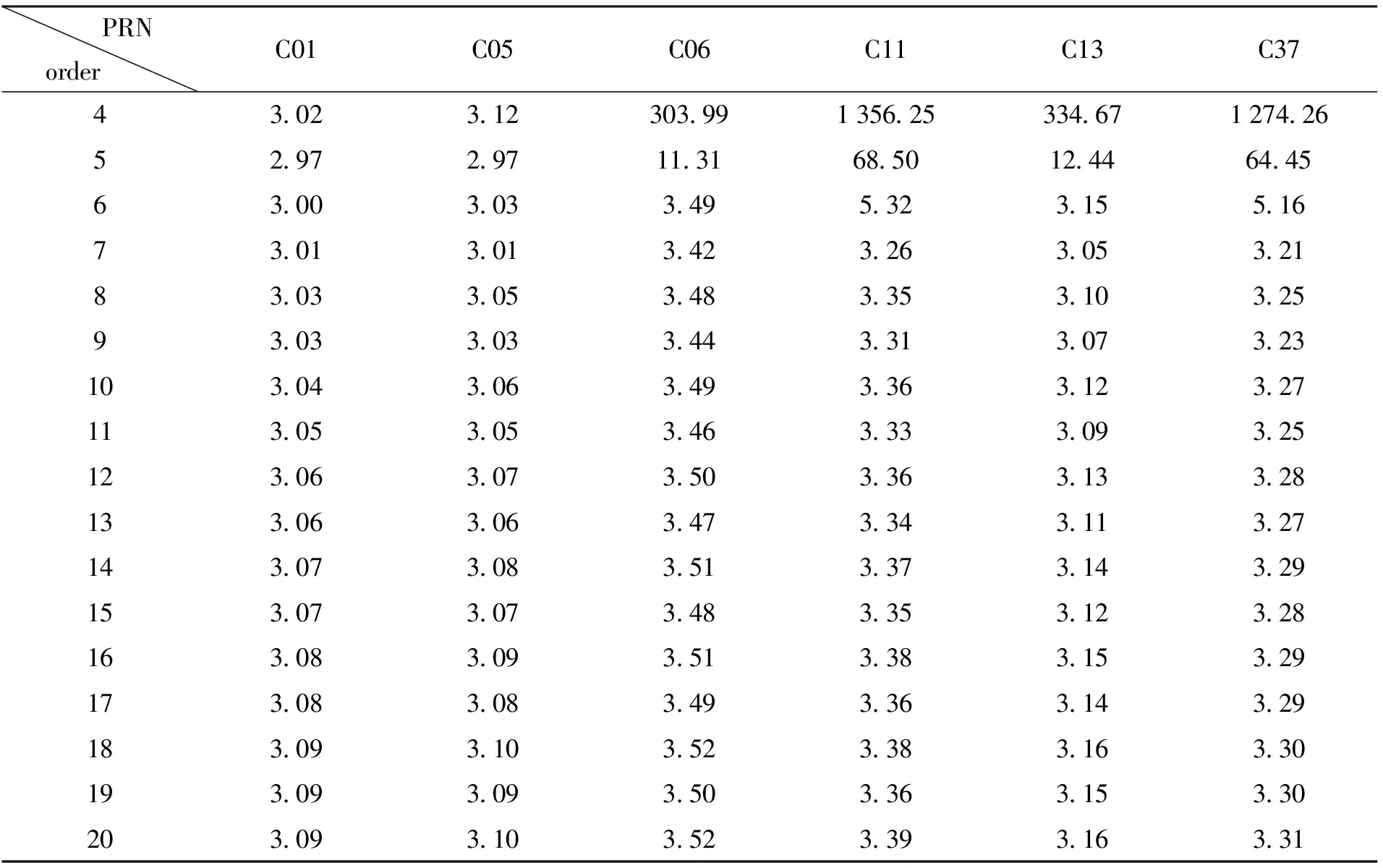
表3 不同插值阶次下滑动式Lagrange插值法精度统计(单位： mm)Table 3 Accuracy statistics of sliding Lagrange interpolation with different interpolation orders (unit: mm)

通过分析可知：

(1)对比32颗卫星在各阶次下采用两种方法插值的结果发现，滑动式Lagrange插值法的精度高于同阶次非滑动式Lagrange插值法。当阶次为4时，两种方法插值误差统计的均方根误差比较大。所有卫星插值结果的统计表明，非滑动式和滑动式Lagrange插值结果的均方根误差平均值分别为1 629.47 mm和908.13 mm，滑动式精度较非滑动式提高79.43%。由其余阶次的统计结果可知，滑动式插值精度较非滑动式均有提高，尤其是中地球轨道卫星和倾斜地球同步轨道卫星，提高幅度大都在50%以上。

(2)地球同步静止轨道卫星受插值方法和插值阶次的影响远小于中地球轨道卫星和倾斜地球同步轨道卫星。对于地球同步静止轨道卫星，采用非滑动式Lagrange插值，当插值阶次较低时，均方根误差在4 mm以内，随着阶次的增加，误差呈逐渐增大的趋势。当阶次为20时，地球同步静止轨道、中地球轨道和倾斜地球同步轨道3类卫星的均方根误差均值分别为1 972.66 mm，2 050.71 mm和1 935.66 mm，中地球轨道卫星和倾斜地球同步轨道卫星的统计误差随阶次增加均呈 “U” 字形。采用滑动式Lagrange插值时，地球同步静止轨道卫星的均方根误差随阶次的增加几乎不变，中地球轨道卫星和倾斜地球同步轨道卫星在4～5阶时均方根误差较大，随阶次增加，均方根误差变化幅度较小。另外，通过对地球同步静止轨道卫星的最佳插值阶次统计发现，最佳插值阶次的精度较4阶插值结果仅提高4%左右(约0.1 mm)。

(3)非滑动式Lagrange插值法受阶次的影响明显大于滑动式Lagrange插值法。整体上看，使用非滑动式Lagrange插值时，插值误差随阶次的增加近似呈 “U” 字形，即插值阶次较低或者较高时，误差均比较大，插值阶次在7～9附近时，误差较小；使用滑动式Lagrange插值时，插值误差在阶次为4和5时，误差比较大，随着阶次的增加，误差变化基本趋于稳定。

为研究插值误差的变化规律，我们对各个时刻的插值误差进行分析， 3类卫星各选一颗进行分析(C01，C06和C11)，图3～图5分别给出了3颗卫星不同情况下各个时刻的误差分布情况，图中z轴表示在某一插值历元下，卫星位置的综合插值误差。

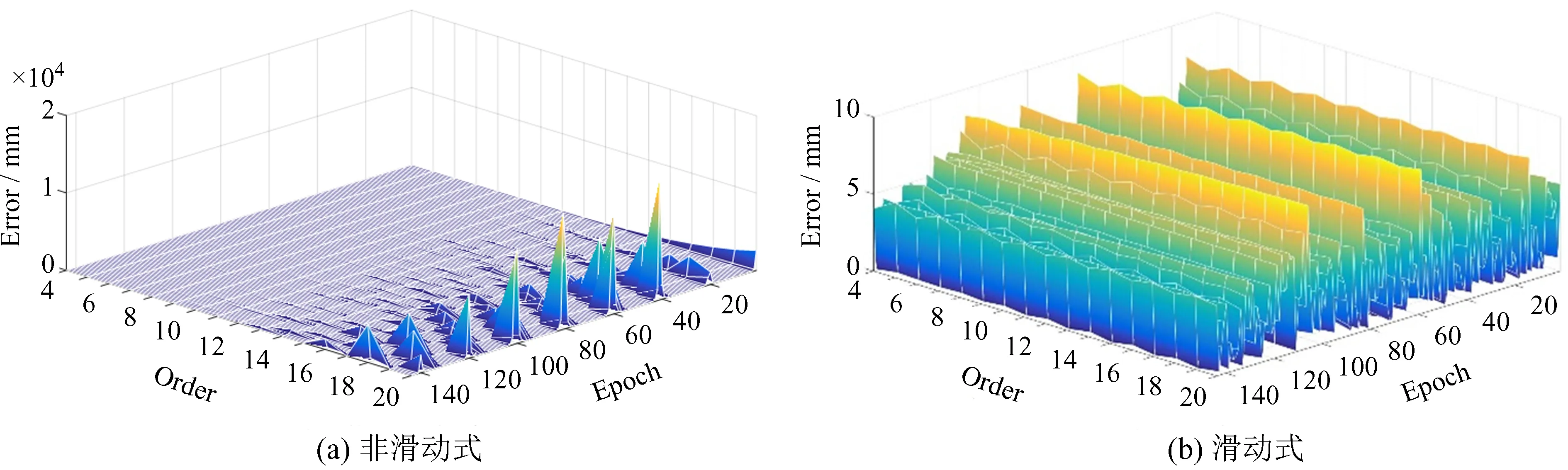
图3 不同插值阶次下C01卫星插值误差的分布情况Fig.3 Interpolation error distribution of PRN C01 under different interpolation orders

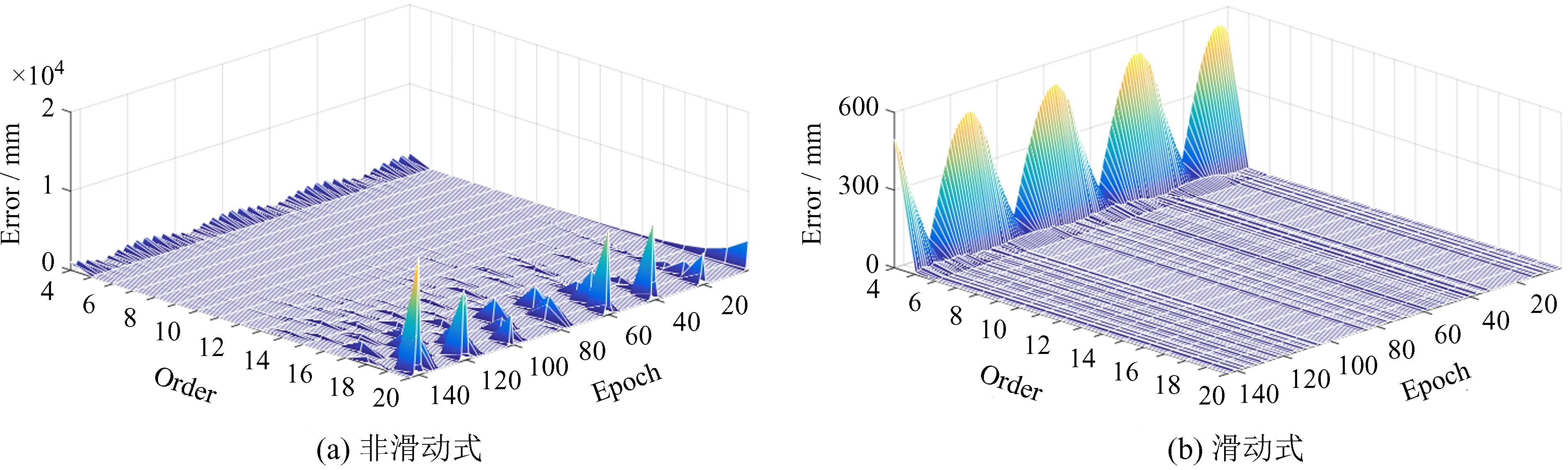
图4 不同插值阶次下C06卫星插值误差的分布情况Fig.4 Interpolation error distribution of PRN C06 under different interpolation orders

图5 不同插值阶次下C11卫星插值误差的分布情况Fig.5 Interpolation error distribution of PRN C11 under different interpolation orders

由图3～图5(a)可知，采用非滑动式Lagrange插值，当插值阶次增加到10阶以上时，插值过程中存在部分插值时刻误差异常的情况。随着阶次的增加，异常值出现的频率相对变少，但数值却逐渐变大。我们对异常值进行分析发现，大多出现在插值区间两端，即异常值的出现主要是受 “龙格” 现象的影响。滑动式Lagrange插值时可保证插值时刻位于区间中心，能有效避免 “龙格” 现象，故出现异常值的概率较小，如图3～图5(b)，随着插值阶次的增加，滑动式Lagrange插值结果未发现异常值，误差变化均比较平缓。

通过分析各阶次插值误差的变化规律发现，插值误差随着插值历元的增加呈现一定的周期性，并且当插值阶次较小时，规律性表现较为明显。对各颗卫星3个方向的误差作功率谱分析可知，低阶插值误差的周期性与其精密星历的周期性一致。这是因为插值阶次较小时，插值所使用的原始数据较少，各时刻的插值结果受原始数据规律的影响比较大，随着插值阶次的增加，各时刻的插值结果受到较多数据的作用，规律性没有表现地那么强烈，这也解释了图中为何随着插值阶次的增加，周期性反而未表现出来。另外，地球同步静止轨道卫星插值误差的周期性并不明显，这也说明了地球同步静止轨道卫星的插值精度优于中地球轨道卫星和倾斜地球同步轨道卫星。

2.2 两种方法最佳插值阶次精度对比

同阶次插值情况下，非滑动式Lagrange插值法的效率较滑动式高，但插值精度相对较低。为研究对比两种方法的最佳插值精度，我们提取各颗实验卫星的最佳插值阶次，统计结果见表4。在两种方法各自的最佳插值阶次下，对各颗卫星的插值结果进行统计，并以均方根误差作为精度评价指标，统计结果见图6。

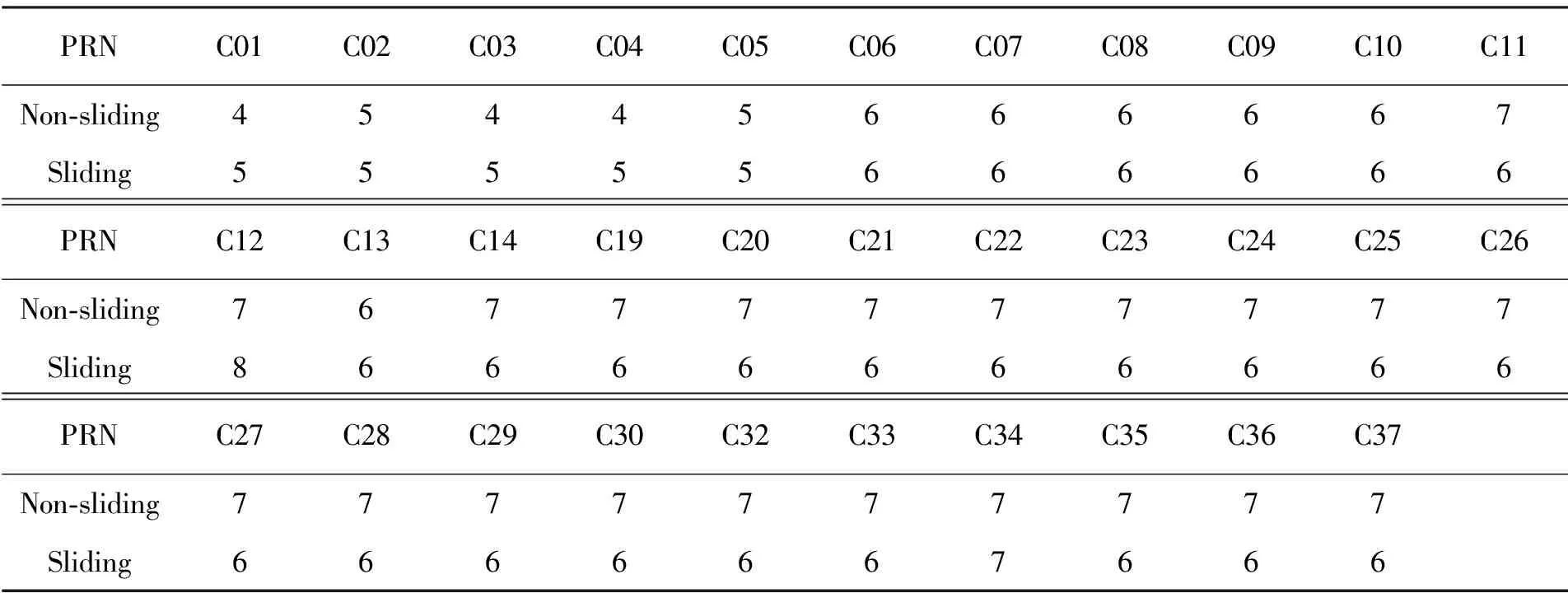
表4 非滑动式和滑动式Lagrange插值法最佳插值阶次Table 4 The best interpolation order of the non-sliding and sliding Lagrange interpolation methods

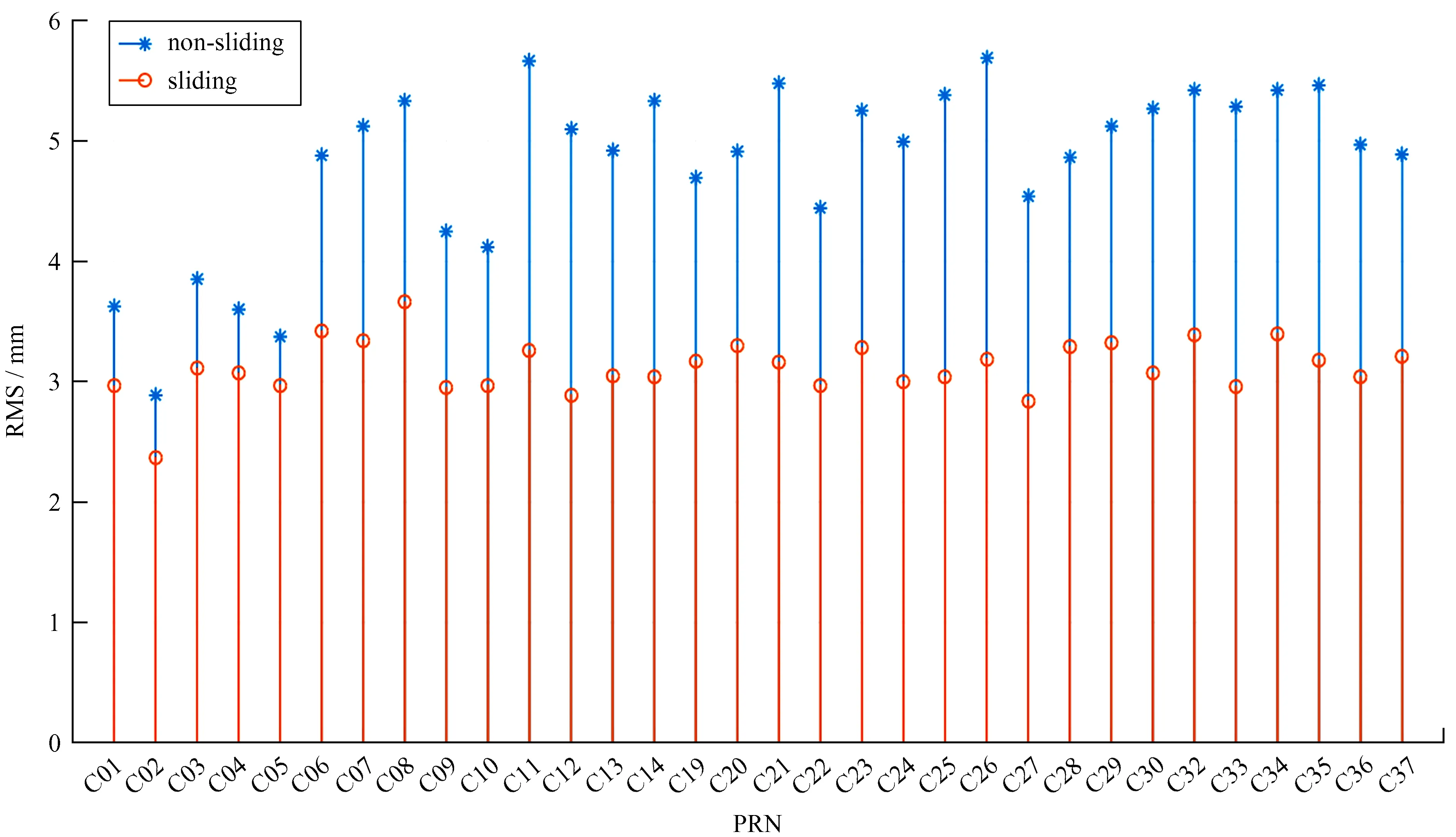
图6 非滑动式和滑动式Lagrange插值法最佳阶次插值精度统计Fig.6 Statistics of the best order interpolation accuracy of the non-sliding and sliding Lagrange interpolation methods

由表4可知，各颗卫星采用非滑动式和滑动式Lagrange插值法的最佳插值阶次均在4～8阶之间，两种方法的最佳插值阶次相差在1以内，其中，12.5%的卫星非滑动式算法插值阶次较低，59.4%的卫星滑动式算法插值阶次较低，28.1%的插值阶次相等。3类卫星中，地球同步静止轨道卫星的最佳插值阶次主要为4阶和5阶，低于倾斜地球同步轨道卫星的6阶，中地球轨道卫星的最佳插值阶次相对最高，主要为6～7阶，个别情况下为8阶。

由图6可知，各颗卫星采用最佳插值阶次时，滑动式Lagrange插值精度均高于非滑动式，较非滑动式可提高11.96%～44.01%。另外，地球同步静止轨道卫星在插值阶次更小的情况下，插值精度同样优于中地球轨道卫星和倾斜地球同步轨道卫星，也说明地球同步静止轨道卫星的轨道数据更为稳定，中地球轨道卫星和倾斜地球同步轨道卫星的插值精度相似。

3 结 语

本文采用滑动式Lagrange插值法和非滑动式Lagrange插值法对北斗卫星导航系统3类卫星的精密星历进行插值，对两种方法及3类卫星的插值精度进行研究。本文以三维方式较为形象地展示了两种插值方式下，3类卫星插值精度与插值阶次的关系，同时对相同阶次下各类卫星的插值精度进行了统计分析。当插值阶次较低时，卫星的插值精度受原始精密星历的影响较大，呈现同样的规律性，其中，地球同步静止轨道卫星受到的影响低于中地球轨道卫星和倾斜地球同步轨道卫星，随着插值阶次的增加，误差的规律性表现逐渐变弱。3类卫星采用两种方法插值时的最佳插值阶次相差均在1以内，使用最佳阶次插值时，滑动式Lagrange插值精度较非滑动式可提高11.96%～44.01%。总的来说，3类卫星中，地球同步静止轨道卫星在相同插值阶次及最佳插值阶次下插值精度均优于中地球轨道卫星和倾斜地球同步轨道卫星，且地球同步静止轨道卫星的最佳插值阶次也较低；两种方法中，滑动式Lagrange插值精度优于非滑动式。在实际使用时，若数据量较多，滑动式Lagrange插值法的计算量明显增大，可在综合考虑插值精度和插值效率的情况下，将两种方法组合使用。