基于零拷贝的脉冲星GPU相干消色散算法*

王博群，张海龙,3,4，王 杰,4，冶鑫晨，王万琼， 李 嘉，张 萌，张亚州

(1. 中国科学院新疆天文台，新疆 乌鲁木齐 830011；2. 中国科学院大学，北京 100049； 3. 中国科学院射电天文重点实验室，江苏 南京 210008；4. 国家天文科学数据中心，北京 100101)

脉冲星是快速旋转的中子星，具有极强的磁场，1967年由Bell女士首次发现。自此，射电脉冲星成为现代天文学的重要研究方向之一。以射电脉冲星作为工具，可以开展高精度计时和授时、天体动力学和天体测量、强场下的引力物理、太阳系外行星、星系和星际介质、超致密物质以及极端环境下的等离子物理等方面的研究[1]。近年来，利用毫秒脉冲星进行引力波探测、脉冲星导航等研究逐渐兴起，高精度脉冲星的观测技术研究成为射电天文学的热门问题。

脉冲星的辐射极其微弱，要求射电望远镜具备很高的灵敏度。建造大口径天线、降低接收机的系统噪声和增加接收机的频带宽度是提高灵敏度的重要方法，其中增大观测带宽是经济、可行的策略，但是带宽不能无限增大。增大观测带宽，一方面给后续数据处理带来巨大压力，另一方面星际介质会对脉冲星信号产生严重的色散影响，造成脉冲轮廓的展宽和变形，严重时甚至可能无法观测到脉冲轮廓。因此在进行脉冲星相关研究时，必须对脉冲星信号进行消色散处理。

近年来，基于图形处理器的并行计算技术已成为高性能计算领域的研究热点，利用图形处理器可以大大提高科学分析、仿真等应用程序的运行速度[2]。英伟达(NVIDIA)推出的统一计算设备架构可使图形处理器解决相对复杂的问题[3]，为计算平台的构建提供了保障。国际上，使用中央处理器 + 图形处理器的异构计算平台进行脉冲信号的实时处理已成为主流。通过使用图形处理器对观测数据进行消色散处理，可降低中央处理器负载，并显著提高计算系统的性能。

本文针对脉冲星观测数据，首先分析了图形处理器消色散的工作原理，然后通过实验研究了图形处理器消色散算法的性能瓶颈，最后设计并实现了基于零拷贝的图形处理器相干消色散算法，并通过实验验证了算法的性能。

1 色散与消色散算法

星际介质是低温的等离子体，脉冲星的电磁辐射通过星际介质到达地球时产生色散，使得高频成分先到达，低频成分后到达。色散是脉冲信号最重要的特征，常用色散度(Dispersion Measure, DM)表示，它是脉冲星与地球的视向距离上电子密度的积分，用公式表示为

(1)

其中，ne为电子数密度；d为脉冲星与观测望远镜的视向距离。由星际介质导致频率f1，f2的观测时延Δt为

(2)

脉冲星信号消色散方法有两种，即非相干消色散和相干消色散。非相干消色散是把观测带宽为BW的时域信号由滤波器分成若干狭窄通道，然后在时域上把每个通道信号按(2)式提供的时延量进行平移，最后将所有通道信号幅度累加，得到最终的信号序列[4]。相干消色散将星际介质对脉冲星信号的影响等效为滤波器，通常的做法是将望远镜接收的信号进行傅里叶变换，然后乘以等效滤波器传递函数的反函数(chirp函数)，再将结果进行傅里叶逆变换，得到时域上的脉冲星原始信号[5]。

星际介质传递函数可分解为幅度响应和频率响应。等效滤波器需要同时对信号的幅度和相位进行修正，由此可得离散chirp函数为[6]

(3)

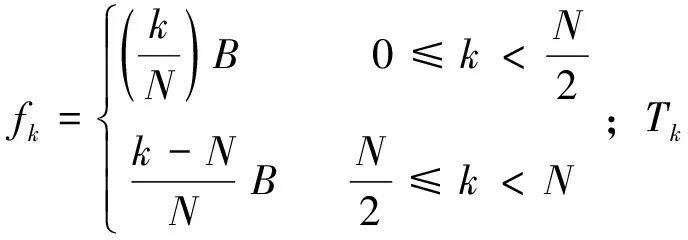
2 零拷贝

中央处理器 + 图形处理器的异构程序执行模型如图1，核心思想是将串行代码放置在主机端(中央处理器)执行，而将并行代码放置在设备端(图形处理器)执行，借助图形处理器多线程减少计算开销。该模型假定主机和设备都在动态随机存取存储器(Dynamic Random Access Memory, DRAM)中保持独立的存储空间，分别称为主机存储器和设备存储器。在程序执行时，需要将预处理数据从主机存储器拷贝到设备存储器，而在图形处理器处理结束后，还要将运行结果拷贝回主机存储器，造成不小的通信开销。

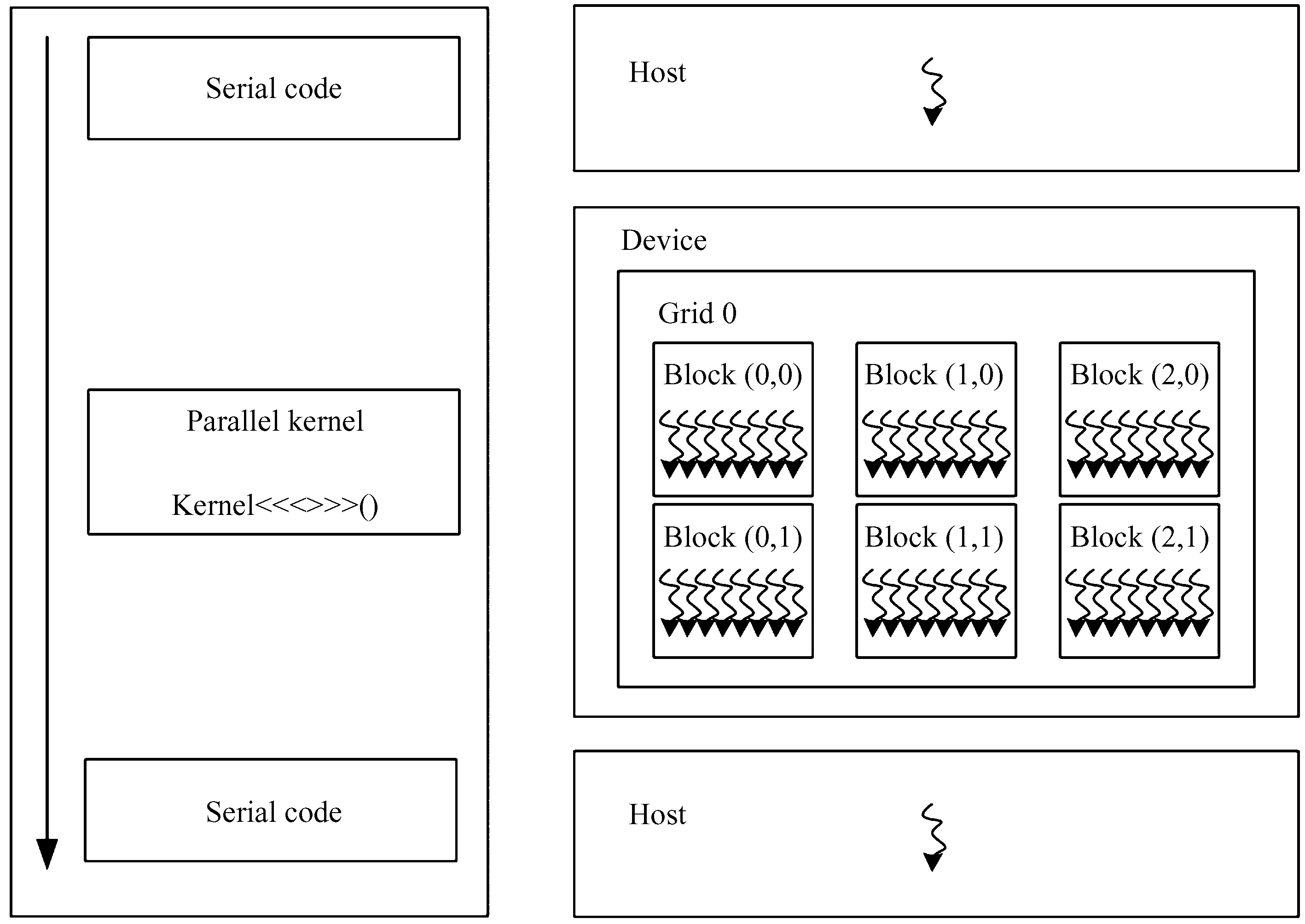
图1 异构程序执行模型Fig.1 Heterogeneous program execution model

零拷贝是指图形处理器直接映射主机内存并通过PCIe访问而无需进行显式内存传输[7]。它需要使用锁页映射内存，核函数线程可直接访问主机内存，从而减少内存拷贝开销。但因为数据不会在图形处理器中进行缓存，所以锁页映射内存只能读取和写入一次，多次读写会降低效率，这是零拷贝的局限性。

零拷贝的代码如图2，其中cudaGetDeviceProperties()返回的prop通过调用canMapHostMemory检查当前图形处理器是否支持将主机内存映射到设备的地址空间，通过cudaDeviceMapHost调用cudaSetDeviceFlags()启动锁页内存映射。然后使用cudaHostAlloc()分配锁页映射主机内存，并通过函数cudaHostGetDevicePointer()获得指向映射设备地址空间的指针。在零拷贝代码中，Kernel()可以使用指针H_MAP引用锁页主机内存，使用方式与调用H_MAP操作设备内存完全相同。

图2 零拷贝代码Fig.2 The code of zero-copy

3 基于零拷贝的相干消色散算法

望远镜在接收脉冲星信号时受到其他信号的干扰，这种射频干扰(Radio Frequency Interference,

RFI)可定义为由人类活动造成的不良射电信号。射频干扰轻则降低脉冲星数据的质量，影响后续的科学研究；重则造成脉冲信号丢失，导致有用的信号完全淹没在噪声中。因此必须对观测数据进行射频干扰消减。射频干扰可以分为窄带干扰和宽带干扰，全球定位系统(Global Positioning System, GPS)的通信信号、飞机通讯信号及调频广播信号等都属于窄带干扰，它们在频域上是窄带的，但因为持续时间长，所以在时域上长期存在；雷电、高压电缆、电子围栏和其他能够引起瞬态电泳的信号属于宽带干扰，它们在时域上是局部的，但会污染多个频域通道并因此表现出宽带特性。

由于宽频带干扰在频域内不易识别，而在时域内表现为短时强脉冲,所以在时域进行宽带射频干扰的消减，具体方法是：

(1)每次取数据块大小为B，由n个点组成，即B1，B2，…，Bn；

(2)求数据块值的均方根；

(3)使用均方根替代B中超过s·rms的数据，其中，s是设置的全局宽带阈值，用公式表示为

(4)

窄带干扰在时间上是连续存在的，在时域上很难将其分离，而在频域上表现为某些突出的尖峰，所以在频域进行窄带射频干扰的消减，具体方法是：

(1)将经过宽带射频干扰消减的数据块B变换至频域并用F表示，大小为m，m=n/2+1；

(2)计算F中的每一个点F1,F2, …,Fm的模|F1|, |F2|, …, |Fm|，然后求模的平均值(mean)；

(3)生成长度为m的滤波器K，如果|Fi|大于u·mean，令Ki=0，否则Ki=1，其中u是设置的全局窄带阈值；

(4)将K与F相乘，得到消除窄带射频干扰后的频域序列。用公式表示为

F=F·K，

(5)

在相干消色散算法中，需要将时域序列变换至频域进行处理，这就要求对数据进行离散傅里叶变换。为了使傅里叶变换更加高效，首先需要对原始数据进行分块处理，然后分别将每一块进行离散傅里叶变换，乘以星际介质的传递函数进行消色散后，再进行逆变换，得到最终的时间序列。

传统的中央处理器使用FFTW(the Faster Fourier Transform in the West)进行离散傅里叶变换，FFTW是一个快速计算离散傅里叶变换的标准C程序集，是目前公认速度最快的开源快速傅里叶变换程序[8]。在NVIDIA GPU上进行离散傅里叶变换需要使用cuFFT[9]，cuFFT提供了经过大量优化和广泛测试的快速傅里叶变换程序库，用户可以借助图形处理器强大的计算能力进行快速变换。

图3给出从实数到复数的图形处理器离散傅里叶变换核心代码。首先定义处理的批次和每一批的数据量N。然后分别定义cufftComplex和cufftReal类型的指针，host_in和host_out分别代表主机端(中央处理器)输入输出数组，device_in和device_out代表设备端(图形处理器)的输入输出数组，使用cufftHandle定义cuFFT句柄，即一个执行计划。接着使用一维的cufftPlan1d对plan进行构造，通过使用批次控制告知图形处理器需要进行多少次一维变换和每次变换的数据量，实现了分别对不同块进行离散傅里叶变换。

图3 从实数到复数的离散傅里叶变换核心代码Fig.3 The core code of R2C DFT

之后为主机端数组申请锁页映射内存，使用零拷贝完成内存到显存的映射，节省了内存拷贝开销，核心代码见图2。内存分配完毕后，使用cufftExecR2C执行傅里叶变换并将结果写入device_out。值得注意的是，cuFFT在执行从实数到复数的变换时会自动去除离散傅里叶变换的对称部分，即如果实数的个数为N，那么得到的复数只有N/2 + 1个。

为了最大化指令吞吐量，核函数中的数学计算全部使用CUDA提供的固有函数，使用sinf和cosf替换传统的sin和cos，前者能够在不影响最终结果的前提下加快运行速度。此外，根据文[10]的建议，在离散傅里叶变换运行过程中采取以下优化策略：

(1)通过对数据进行截取，保证数据长度是2的幂级数，加快了运行速度；

(2)通过使用单精度变换，使用额外空间进行离散傅里叶变换结果缓存(out of place)，提高运行效率；

(3)通过使用多批次变换进行离散傅里叶变换，而不是重复使用cufftPlan1d，缩短了运行时间。

4 实验结果

算法测试所使用的开发设备如表1，操作平台为Windows 10，开发工具为Visual Studio Community 2015，NVIDIA Visual Profiler，开发语言为C，CUDA C，Python。

表1 开发设备Table 1 Development equipment

本文使用真实的脉冲星基带数据进行算法测试。数据格式为双极化8 bit采样的PSRDADA，观测源为J0437-4715，观测信息如表2。基带数据记录时间约为8 s，大小为12.8 GB。

表2 J0437-4715观测信息Table 2 J0437-4715 observation information

为验证本文算法的正确性，我们进行以下实验：首先对11.72 GB的原始数据进行折叠，生成轮廓图作为对照。然后固定数据块大小为16 MB，使用本文算法分别处理50，250和750个数据块，其数据量分别为0.78 GB，3.91 GB和11.72 GB。实验结果如图4，(a)代表原始数据折叠未进行消色散，(b)，(c)和(d)分别代表数据块个数为50，250和750时消色散后得到的脉冲轮廓。

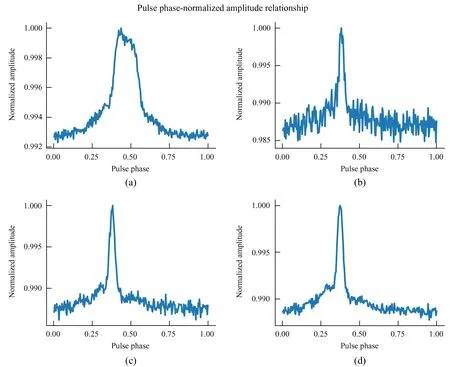
图4 不同情况下的脉冲相位-归一化振幅关系图Fig.4 Pulse phase-normalized amplitude relationship in different situations

对比图4中的(a)和(d)可得，本文算法可以正确地对脉冲信号进行修正，完整展现脉冲轮廓。通过与新疆天文台数据中心的J0437-4715轮廓进行比对，证明所得轮廓的正确性。对比图4(b)，(c)和(d)可知，随着数据块数量的不断增加，所得脉冲轮廓信噪比逐渐提高。

为验证中央处理器算法、传统图形处理器算法以及本文算法(ZGPU)在不同数据量下的执行速度，进行以下实验：首先固定数据块大小为8 M，将每次处理的数据块数量分别设置为10，50，100，200，400，800和1 500，对应数据量为0.08 GB，0.39 GB，0.78 GB，1.56 GB，3.13 GB，6.25 GB和11.72 GB，然后令3种方法分别在每个数据量下运行10次，最后取平均值作为运行时间。此外，为验证设备性能对算法的影响，本实验采用两套设备进行测试，设备型号如表1，实验结果如表3，时间单位为s。

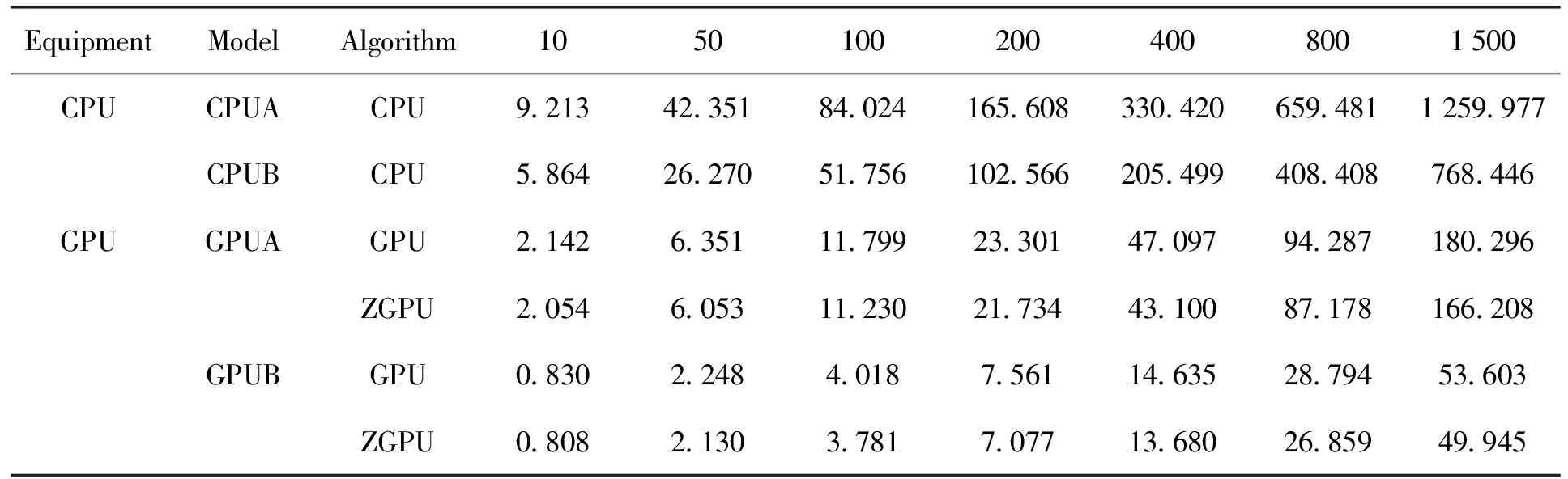
表3 实验结果Table 3 Experimental results

图5 CPUB-CPU与GPUB-ZGPU 数据量-运行时间关系图

图6 GPUB-GPU与GPUB-ZGPU 数据量-运行时间关系图

本文采用模型算法(Model-Algorithm)的方式对算法进行讨论，例如GPUA-GPU即代表运行在GPUA上的传统图形处理器算法。从表3中抽取CPUB-CPU和GPUB-ZGPU做折线图，得到图5；取GPUB-GPU和GPUB-ZGPU做折线图，得到图6；取GPUA-ZGPU和GPUB-ZGPU做折线图得到图7。

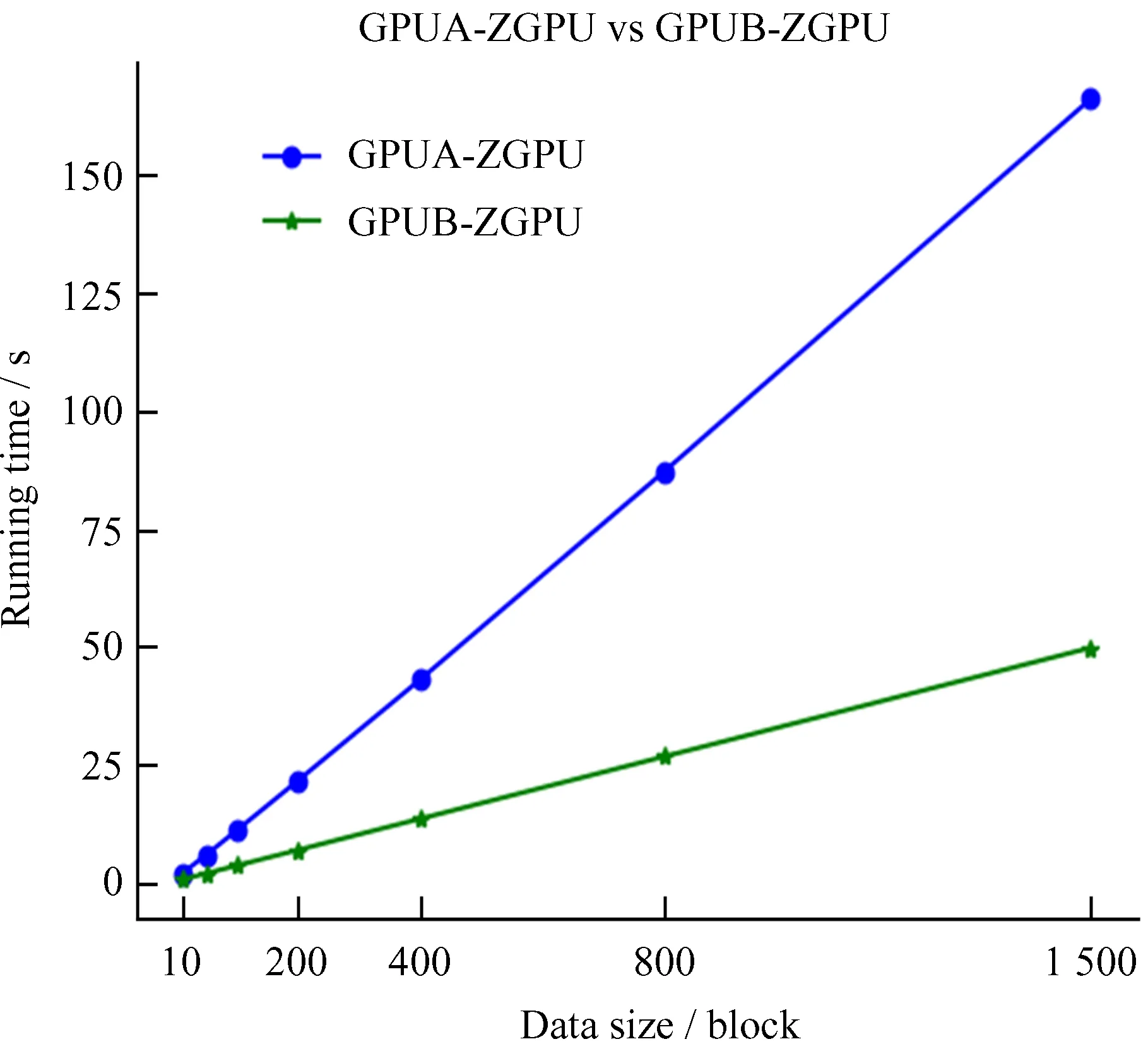
图7 GPUA-ZGPU与GPUB-ZGPU 数据量-运行时间关系图

结合表3分析图5可知：两种算法的执行时间都随着数据量增加而线性增长，但是传统中央处理器算法的平均运行时间远大于本文算法。在数据大小为11.72 GB时，传统中央处理器算法需要768.446 s才能完成消色散，而本文算法仅需49.945 s，速度提升了约15倍。由此可知，本文算法在速度上优于传统的中央处理器算法。

结合表3分析图6可知：两种算法的执行时间都随着数据量增加而线性增长，在数据量较小时，本文算法与传统图形处理器算法的差距不明显，但随着数据量的增加，两种算法的时间差也在线性增长。当数据量分别为400，800和1 500时，两种算法的时间差为0.955 s，1.935 s和3.658 s，即数据量增加2倍，时间差也增加2倍。由此可知，本文算法在数据量较大时优于传统图形处理器算法，数据量越大，本文算法的优势越明显。

结合表3分析图7可知：本文算法在新架构图形处理器上的平均运行时间明显比之前的图形处理器短。在数据量为1 500时，本文算法在GPUA上运行需要166.208 s，而在GPUB上仅需49.945 s，速度提高了约3倍。由此可知，硬件性能是影响本文算法的重要因素。

5 结 论

本文设计实现了基于零拷贝的图形处理器脉冲星相干消色散算法。通过合理构造核函数实现了最大化并行执行，采取零拷贝技术提高了内存吞吐量，使用CUDA内置计算函数优化了指令调用。通过在离散傅里叶变换中对cuFFT进行优化，提高了运行效率。结合真实数据测试表明，本文实现的算法优于传统的中央处理器算法，且在数据量较大时优于传统的图形处理器算法。基于零拷贝的图形处理器消色散算法为高效实现脉冲星数据处理相关研究提供了一种新的解决思路。实验数据及源代码可在新疆天文台数据中心[11]获取。

致谢：本文得到中国虚拟天文台、国家天文科学数据中心和中国科学院科学数据中心体系提供的数据资源和技术支持，在此表示感谢。