关于Chebyshev多项式的首尾差r-循环矩阵的行列式

邱 涛， 雷 林， 何承源

（西华大学 理学院，四川 成都610039）

循环矩阵因其特殊的结构特征，而被广泛应用于许多现代工程科学领域［1-5］，如编码理论、数字图像识别、密码学、信号处理、石油勘测等.近年来，在矩阵理论研究领域，对特殊循环矩阵的研究一直是一个热门的方向，国内外大量学者对经典循环矩阵［6］不断进行推广和延伸.主要研究包含特殊数列及多项式的特殊循环矩阵的行列式、逆矩阵、谱范数、非奇异性、自反广义逆、特征值、幂运算等性质.

循环矩阵的行列式作为基本的数学工具，在各方面有着重要的作用.文献［7］通过矩阵分解理论，给出了包含Fibonacci与Lucas数列的循环矩阵行列式；文献［8］采用同样的分解原理，将数列推广到Jacobsthal与Jacobsthal-Lucas数列，并给出了行列式的显式表达式；文献［9］研究了H-循环矩阵及H-左循环矩阵的行列式；文献［10-11］给出了H-循环矩阵的判别及求解H-循环矩阵线性系统的快速算法；文献［12］讨论了广义Fibonacci多项式的循环矩阵行列式；文献［13］给出了包含三阶序列的行斜首加尾右循环（RSFPLR）和行斜尾加首左循环（RSLPFL）矩阵的行列式；文献［14-16］将矩阵推广到行首加r尾r右循环（RFPrLrR）和行尾加r首r左循环（RFPrLrL）矩阵，分别给出了包含不同线性递推数列和多项式的行列式.

基于以上研究，本文主要将对H-循环矩阵和行斜首加尾右循环矩阵的研究推广到对首尾差r-循环矩阵的研究，同时把H-左循环矩阵和行斜尾加首左循环矩阵推广到首尾差r-左循环矩阵，这2类矩阵具有更广义的形式.本文利用多项式因式分解逆变换的方法，给出了包含第一、二类Chebyshev多项式的矩阵的行列式，最后通过数值实例对定理进行了验证.

1 预备知识

定义1［17］第一、二类Chebyshev多项式是权函数为且由序列｛1，x，…，x n，…｝在区间［－1，1］上正交化得到的正交多项式，具体表达式为：

其二阶线性递推公式为：

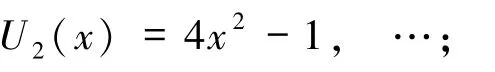
｛Tn（x）｝与｛Un（x）｝的通项公式为：

其中

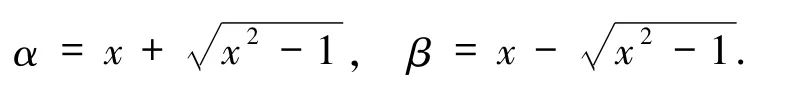
定义2［18］记Mn×n（C）为复数域上n阶矩阵的集合，若矩阵A∈Mn×n（C）有如下形式

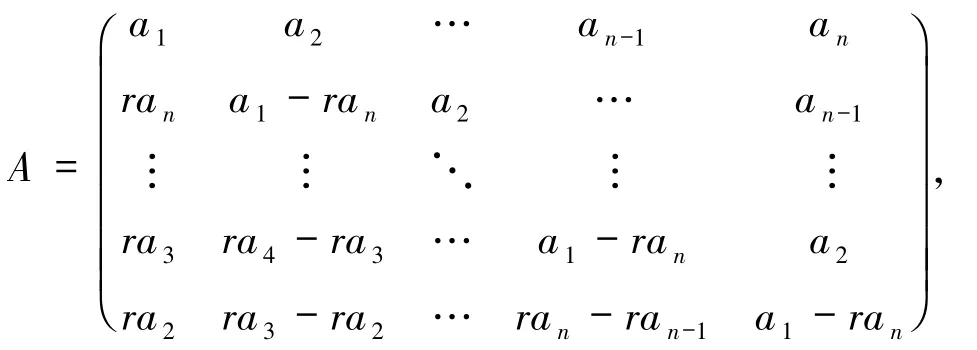
则称矩阵A为首尾差r-循环（FLDcircr）矩阵，简记为A＝FLDcircr（a1，a2，…，a n）.

第一行元素a0，a1，…，a n－1决定了矩阵A的构成：对第i行的行尾元素先乘r，第i行的行首元素再减去第i行的行尾元素，所有元素向右移一位就得到第i＋1行元素.FLDcircr矩阵是一类特殊的循环矩阵，不同于首尾和（FLS）r-循环矩阵［19-20］和行首加r尾r右循环矩阵（RFPrLrR）［14-16］，也不是这2类的特殊情况.当r＝1，则FLDcircr矩阵就是H-循环矩阵［911］；当r＝ －1，则FLDcircr矩阵就是行斜首加尾循环矩阵（RSFPLR）［12-13］.

定义π为n阶基本FLDcircr矩阵，则π的具体表达形式为

π的特征多项式为

且有

规定π0＝In，这里In是n阶单位矩阵.FLDcircr矩阵可由基本FLDcircr矩阵π来表示，有

定义3若矩阵B∈Mn×n（C）有如下形式：

则称B为首尾差r-左循环（FLDLcircr）矩阵，简记为B＝FLDLcircr（a1，a2，…，a n）.

FLDLcircr矩阵的构成规则：对第i行的行首元素先乘r，第i行行尾元素再减去第i行的行首元素，所有元素向左移一位就得到第i＋1行.

引理1［18］设矩阵

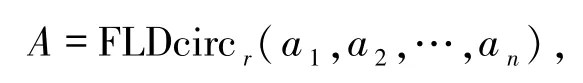
那么A的特征值为

这里 ωi（i＝1，2，…，n）是基本FLDcircr矩阵π的特征值，即ωi是方程

的根.

引理2

其中

ωi（i＝1，2，…，n）是方程（2）的根，s、t是方程

的根，a≠0，c，b，a∈R.

证明

其中s、t是方程的根，根据韦达定理有

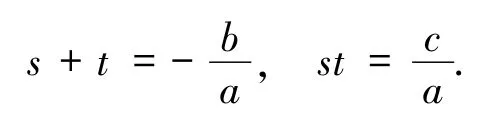
由于ωi是方程（2）的根，则有

其中，Δn－1＝sn－1＋t n－1，Δn＝sn＋t n（下同）.

引理3设

是一个FLDLcircr矩阵，

是一个FLDcircr矩阵，则有

证明容易验证：

其中

进一步可以得到

2 主要结论及其证明

首先，研究关于第一类Chebyshev多项式Tn的首尾差r-循环矩阵及首尾差r-左循环矩阵的行列式，得到的结果和证明如下.

定理1设矩阵C＝FLDcircr（T1，T2，…，Tn），那么

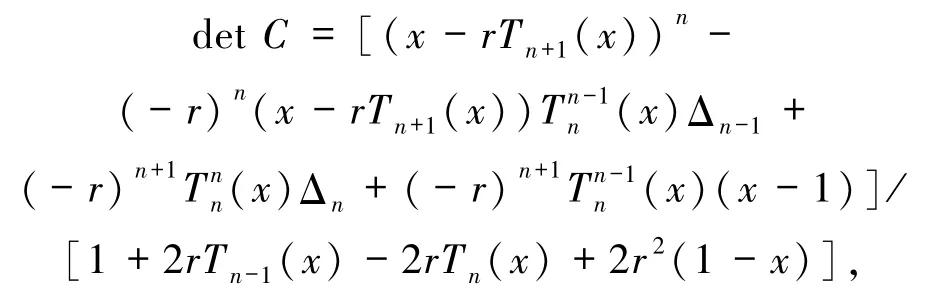
其中

证明矩阵C＝FLDcircr（T1，T2，…，Tn）表示为

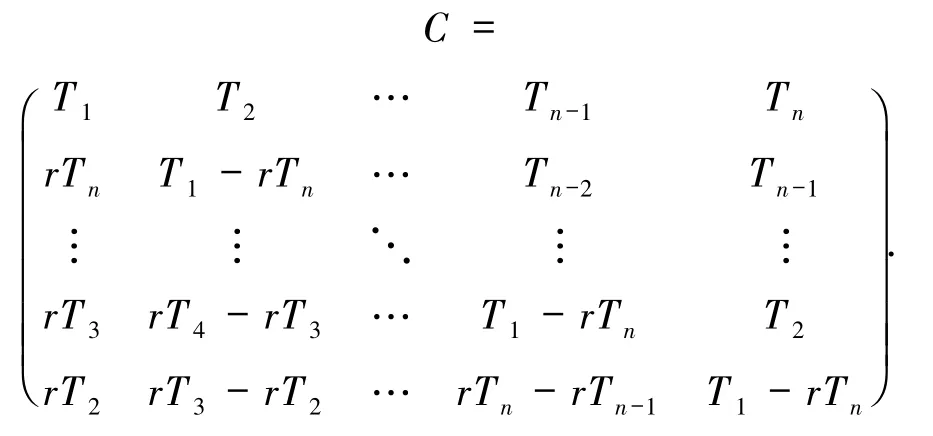
由引理1，可得矩阵C的行列式为

根据引理2，可得

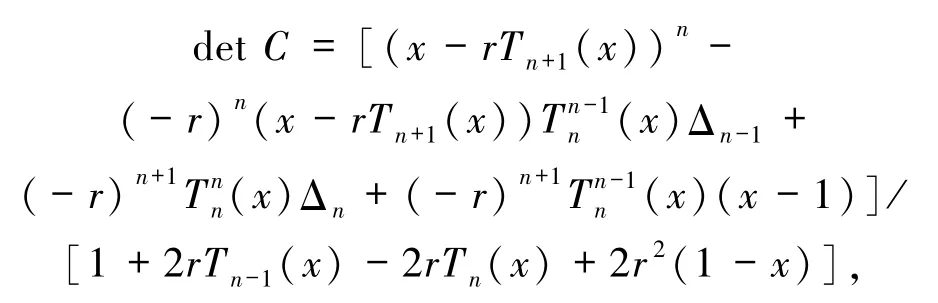
的2个根.

推论1设矩阵

那么

其中

证明矩阵

表示为

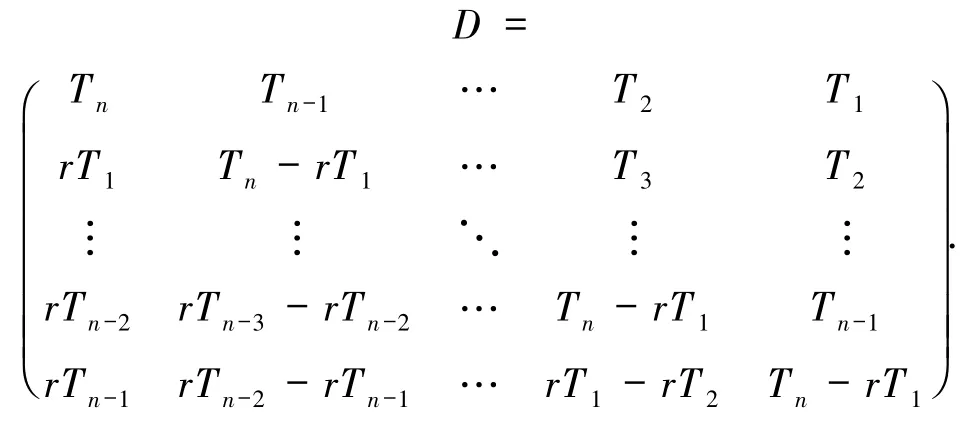
类似定理1的证明，可以得到推论1的结果.

定理2设矩阵

那么

其中

证明由定义3，矩阵

可以表示为

所以，根据引理3有

且由推论1知

故有

其中

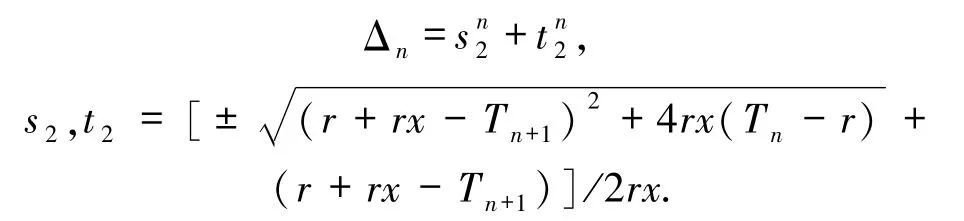
其次，考虑包含第二类Chebyshev多项式Un的首尾差r-循环矩阵及首尾差r-左循环矩阵的行列式，得到的结果和证明如下.

定理3设矩阵

那么

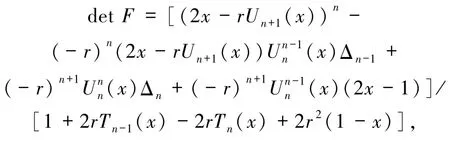
其中

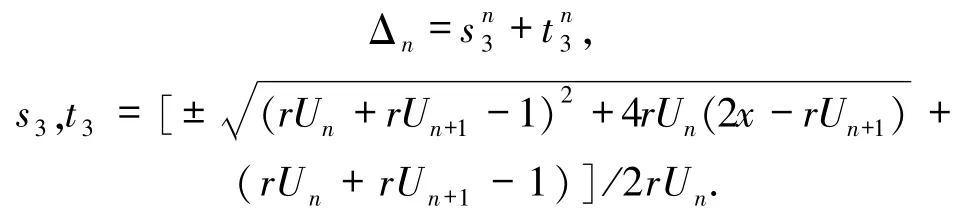
证明矩阵

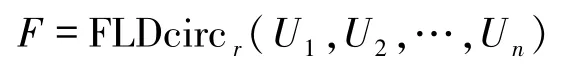
表示为

由引理1，可得矩阵F的行列式为

根据引理2，可得

其中

s3、t3是关于 ωi的方程

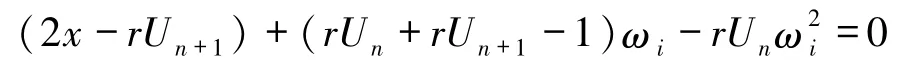
的2个根.

推论2设矩阵

那么

其中

证明矩阵

表示为

类似定理3的证明，可以得到推论2的结果.

定理4设矩阵

那么

其中

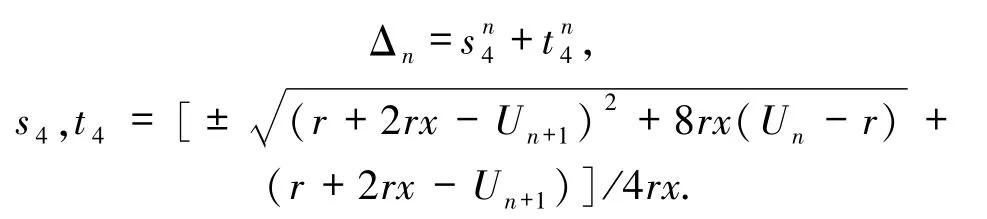
证明由定义3，矩阵

可以表示为

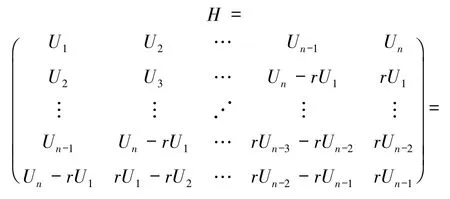
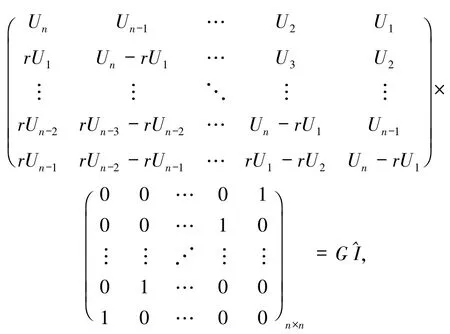
所以，根据引理3有detH＝detGdet，且由推论2知

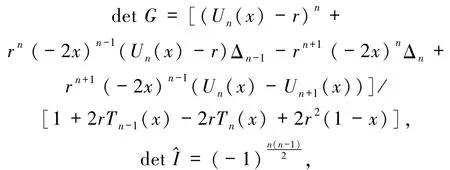
故有

其中

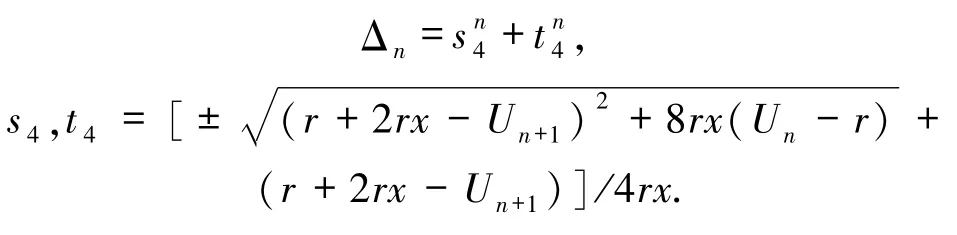
3 数值举例

设3阶矩阵

求矩阵A的行列式.

解由定义1和定义2可知，矩阵A是包含第一类Chebyshev多项式的首尾差r-循环矩阵，其中r＝2，那么A可以简记为A＝FLDcirc2（T1，T2，T3）.根据定理1可以得到

其中

取x＝ －1，则

由定理1可得

当x＝ －1，矩阵根据行列式理论有

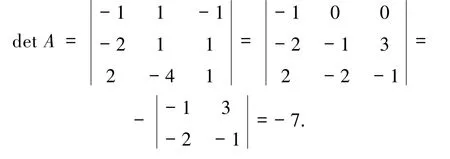
4 结论

通过数值举例，对本文提出的方法进行了验证.利用类似的证明方法，参数r取不同的值，可以将对FLDcircr矩阵和FLDLcircr矩阵的研究推广到其他特殊的循环矩阵，如：当r＝1，可以得到H-循环矩阵和H-左循环矩阵的行列式，见文献［9］；当r＝－1，可以得到行斜首加尾循环矩阵和行斜尾加首左循环矩阵的行列式，见文献［12-13］.利用本文的这些理论也可将矩阵元素推广到二阶线性递推数列、三阶线性序列和多项式，进而研究包含这些特殊数列的特殊循环矩阵行列式及其他性质.